防洪物資調運的數學模型

汪 軍, 孫志紅, 劉信斌

(徐州空軍學院基礎部,江蘇徐州 221000)

防洪物資調運的數學模型

汪 軍, 孫志紅, 劉信斌

(徐州空軍學院基礎部,江蘇徐州 221000)

首先構建防洪物資調運的交通網絡矩陣模型,并利用Dijkstra算法尋找各調運節點之間的最優路線,然后在平時以追求最小總調運費用、緊急情況下以追求最快調運速度為目標建立了防洪物資調運的優化模型,在此過程中引入偏離控制量以便充分考慮各調運節點的需求,討論了調運期、偏離控制量對調運費用的影響,為科學制定調運方案提供依據,較好地解決了防洪物資的調運問題.

物資調運;Dijkstra算法;偏離控制量;調運節點

1 問題背景及重述

2007年5月江蘇省工業與應用數學學會及中國礦業大學聯合主辦了第四屆蘇北數學建模聯賽,聯賽得到包括武漢大學、國防科技大學、中國農業大學等跨及全國12個省市60多所高校的積極參與,本文詣在解決其中的C題——防洪物資調運問題.

2 模型假設

(i)高等級公路與普通級公路的調運速度是恒定且相等的;

(ii)各企業、物資倉庫及國家級倉儲庫之間的物資可以通過公路運輸互相調運且所有公路均可雙向運輸;

(iii)調運物資的運輸車輛是充足的,即一旦確定調運方案,即刻可調運完畢;

(iv)調運節點指生產企業、物資倉庫、國家儲備庫共13個,調運期系指開始實施調運的時間;

(v)只考慮運輸費用,不考慮物資裝卸、儲存等其它費用.

3 變量及符號假設

ri——調運節點i調運后的庫存量(百件)

xij——從調運節點i到調運節點j之間的物資調運量(百件)Mi——調運節點i的最大庫存量(百件)

為了實現城市規劃中各中心城區與邊緣居住綠色分隔，要對當地的實際情況進行調查分析，并根據不同的地理環境，遵循景觀生態學的原理與方法科學合理的布局，從而更好的保護耕地，有效提升耕地綜合利用率。

fi——調運節點i的預測庫存量(百件)

vi——生產企業i的產量(百件/天),i=1,2,3

ti——生產企業i在調運期的生產天數(天)

z——總調運費用(元)

4 問題分析

通過對問題的分析,該地區的公路交通網絡數學模型應該是指包含42個頂點的賦權圖.所謂合理的調運方案就是要在盡可能地滿足各個調運節點需求的前提下,平時盡量使調運費用最小,而在緊急情況下應盡快地將防洪物資調運到各需求點,這些都需要去尋找各調運節點之間的最優路徑,所以這是一個優化問題,可以考慮建立該問題的規劃模型.

5 模型的建立及求解

1.交通網絡模型

在該地區交通網絡圖中調運節點共有13個,包括企業三家、物資倉庫八個、國家儲備庫兩個,為表達方便,我們按企業1,企業2、企業3、物資倉庫1、……、物資倉庫8、國家儲備庫1、國家儲備庫2的順序編號為1到13,防洪物資的調運只限于在13個節點之間進行調運,故需找到它們之間的最優調運路線,平時應以最少運輸成本Wij(i,j=1,2,…,13)為優.這里尋找最優路線時我們用Dijkstra算法來解決.

2.問題2及問題3的模型建立及求解

問題2要求設計一個在重點保證國家級儲備庫的情況下的合理調運方案,為此設從調運節點i到調運節點j的調運量為xij(百件),xij≥0,i,j=1,2,…,13.則調運結束后各個調運節點的庫存量為

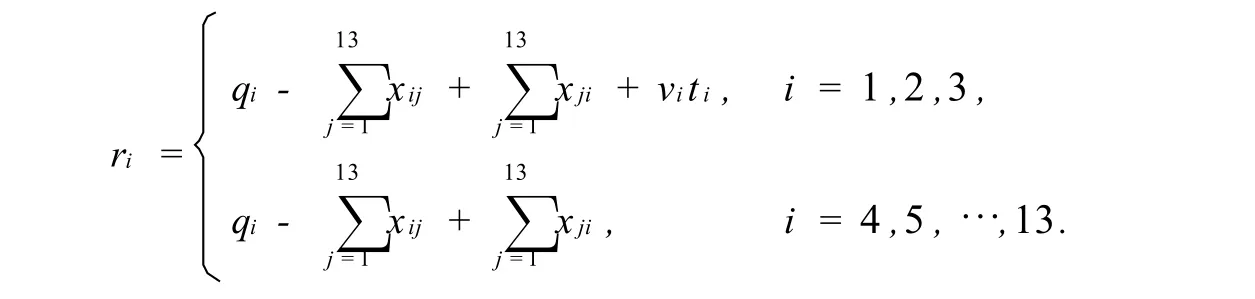
為重點保證國家級儲備庫的庫存,合理調運方案必須使國家級儲備庫的庫存達到或者超過其預測值:ri≥fi,i=12,13.倉庫1到倉庫8的應盡量達到或超過預測庫存,為此考慮用一個偏離控制量ε(ε＞0)來控制,即

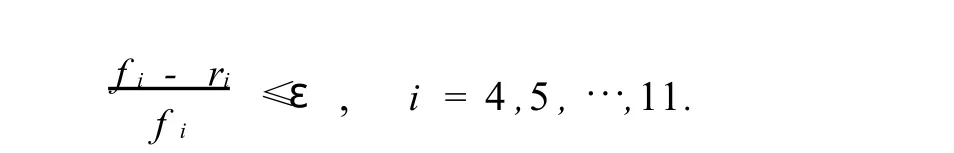
根據調運計劃及各企業生產能力,調運期至少應為8天,才能滿足基本要求,若給定ε=0.05,通過Lingo求解得調運方案見表1.

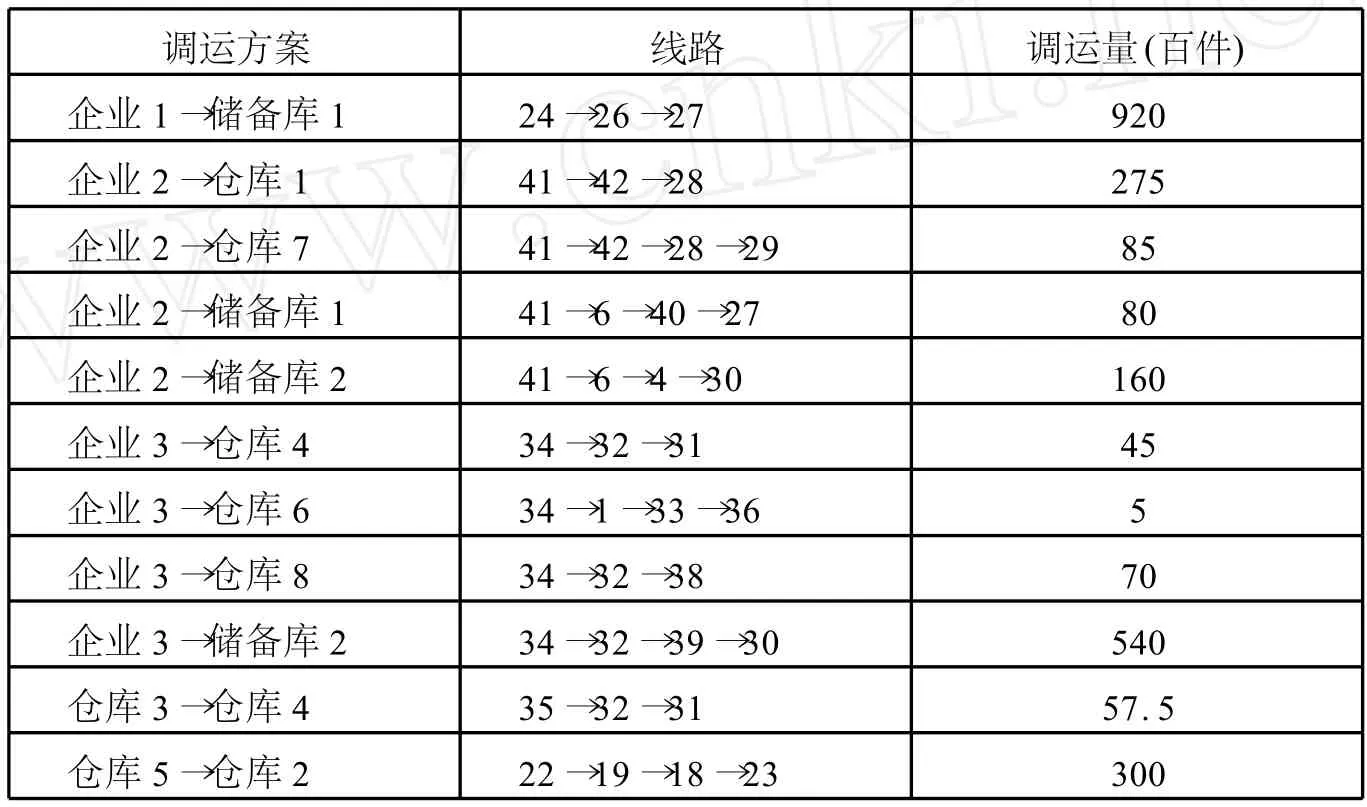
表1 調運期為8天時的最優調運方案

按此方案調運的最低總運輸費用為321680元.

對于問題3,在問題2中令T=20,可以計算求得新的調運方案,此時調運總費用為299763元, 20天后各個調運節點的庫存情況如表2所示.

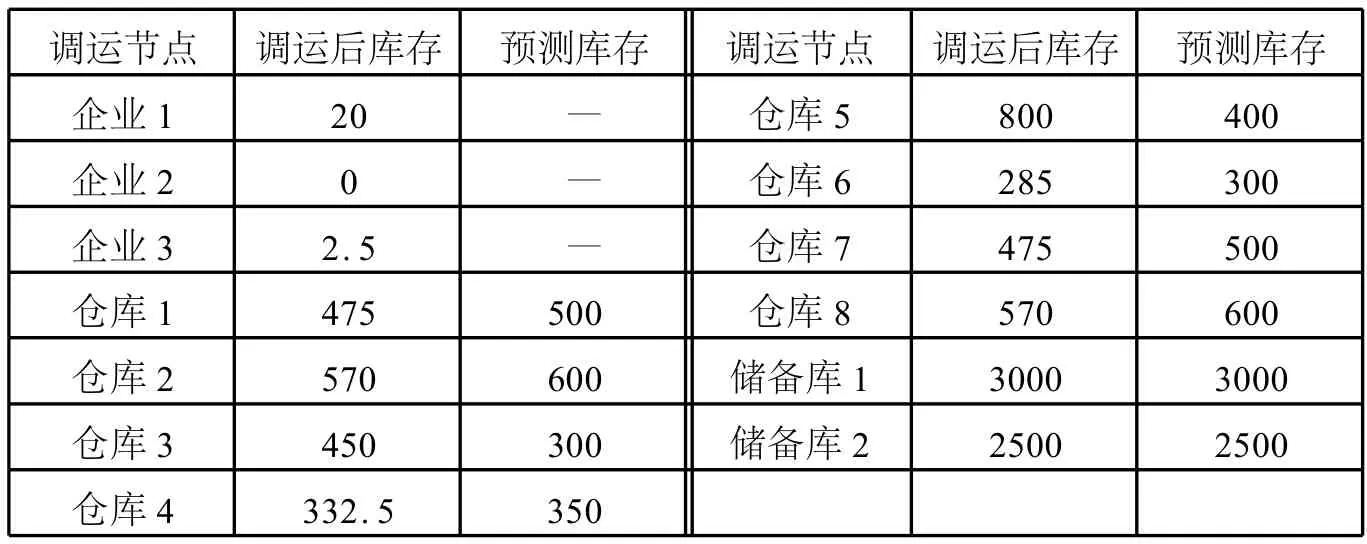
表2 20天后各個調運節點的庫存

3.問題4的模型建立及求解

問題4要求解決汛期部分路段中斷情況下的緊急調運問題,此時應該考慮速度盡可能快,而無須考慮運費.鑒于洪水導致路段中斷,故應構建新的交通網絡賦權圖G(V,E′),其中每條邊的權值為smn,E′為集合E中去除邊○14○23,○11○25,○26○27,⑨○31的集合,利用Dijkstra算法計算各調運節點之間的最短路徑Sij(i,j=1,2,…,13),在問題2中將目標函數修改為

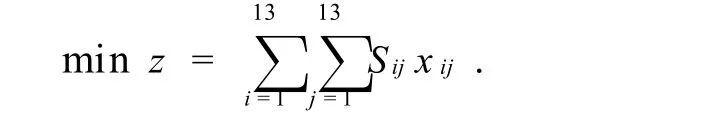
以8天為調運期,在約束條件不變的情況下,得到最優調運方案如表3.

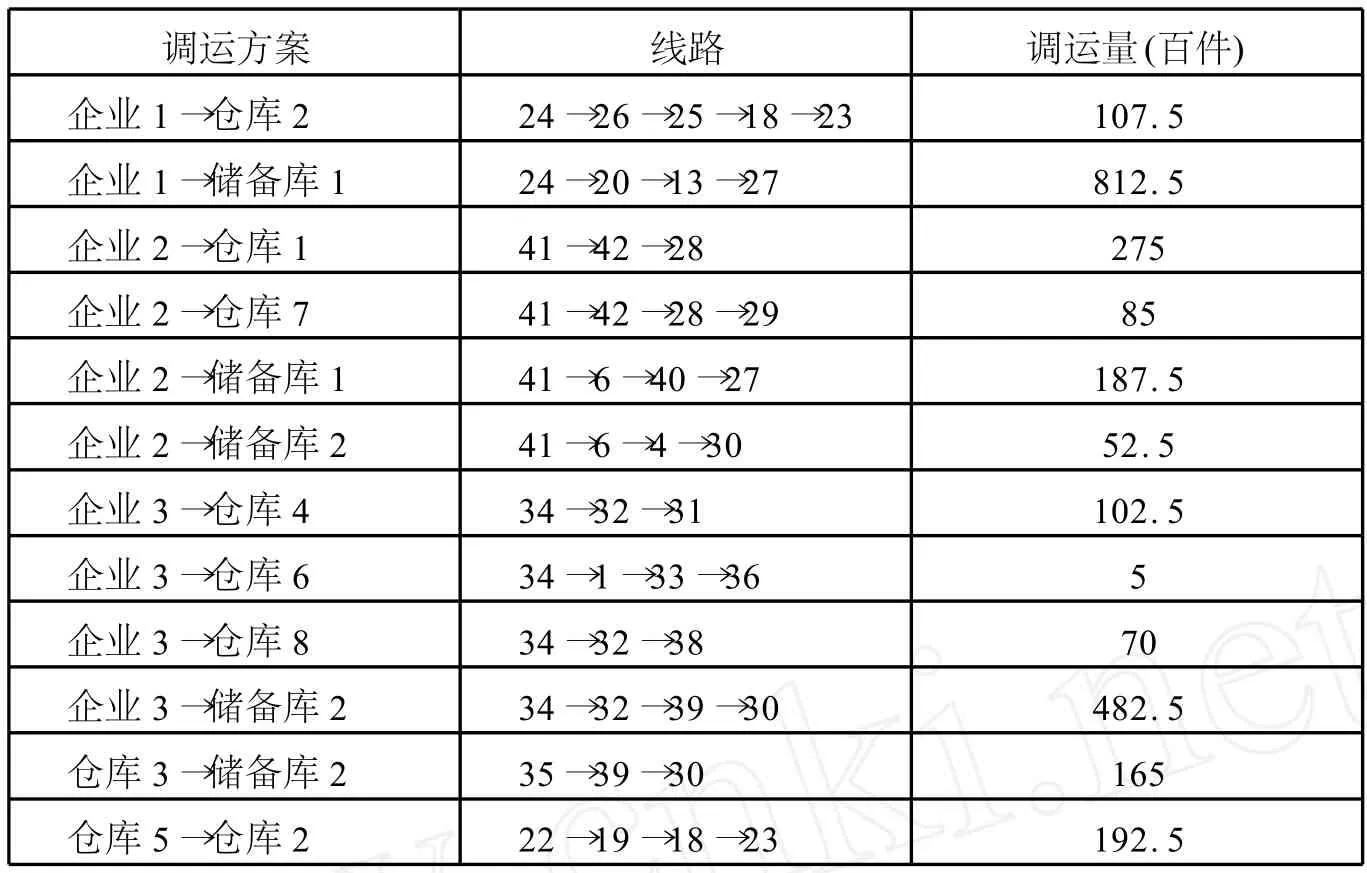
表3 調運期為8天時緊急情況下的最優調運方案

6 模型的進一步討論

1.調運期的長短與運費的關系

在求解問題2和問題3的時候,我們發現,在調運期為8天的時候,總運費為321680元,調運期為20天的時候,總運費為299763元.顯然,調運期的長短對最終運費有著顯著影響.

我們希望能夠找到一個最佳的時間,使得總運費能夠達到最小,同時使各調運點的庫存能夠達到或超過預測值.為此對問題2中的模型進行修改,建立最佳時間模型如下.

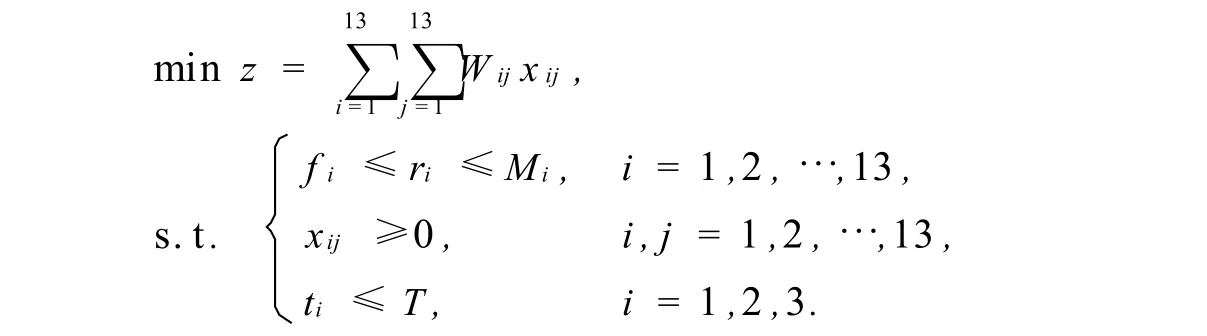
在這個模型中,要求在調運完畢后,各庫的庫存都要達到或超過預測值.令T=8,9,10,…,計算得到調運期與總調運費用之間的關系如圖1.

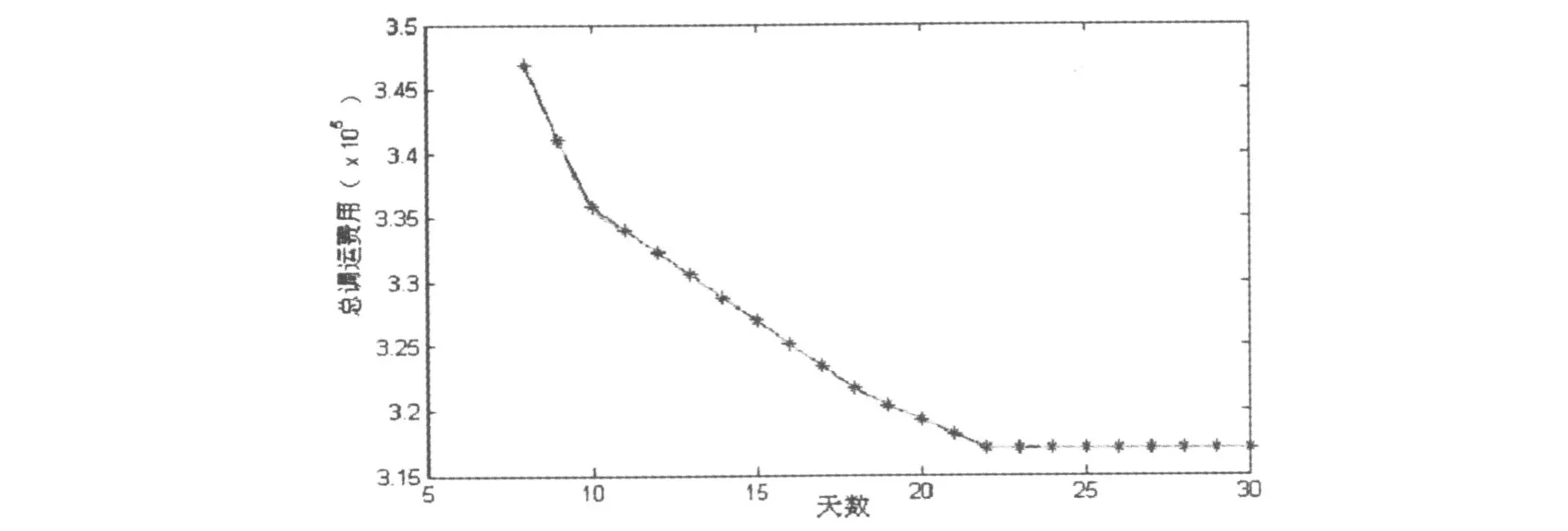
圖1 調運期與總調運費用之間的關系

從圖1可以看出,隨著調運期的增加,總的調運費用不斷下降.當T增加到22天的時候,調運費用趨于平衡,不再發生改變.造成這種情況的原因是,隨著調運期限的增加,企業可用來生產的天數也增加,因而企業能夠運出的物資量也增加,相應的輸出選擇面和靈活度也增加,從而使總運費降低.因此,根據此模型防汛部門可以科學制訂調運期,特別是在準確預測汛期的情況下,對于提前做好科學決策有重要意義.

2.調運期的長短、ε的取值對費用的影響

ε的取值對于費用也有著重要的影響,我們希望能夠找到ε和T對于總費用的影響效果.為此,在問題2的模型中,分別取不同的ε和T值從而得到總調運費用與ε及調運期T的關系如圖2.

圖2 總調運費用與ε及調運期T的關系

從圖2可以看到,總調運費用均隨著偏離控制量ε和物資生產天數T的增加而減少.這是非常符合實際情況的,因為ε的增大使得約束條件減弱,因而總的調運費用降低;物資調運期T的增加使得各個企業的產量增大,故導致調運任務的靈活性增加,因而總的調運費用降低.同時,從圖2可以很明顯地看出:ε波動對總調運費用的影響比物資調運期T的改變對總調運費用的影響要大.所以ε的控制效果是非常明顯的.

[1] 汪軍,等.戰時航空油料的優化調撥[J].南京航空航天大學學報,1999,31(1):112-115.

[2] 姜啟源,等.數學模型[M].北京:高等教育出版社,2004.

[3] 錢頌迪,等.運籌學[M].北京:清華大學出版社,1990.

[4] 袁新生,邵大宏,等.L INGO和Excel在數學建模中的應用[M].北京:科學出版社,2007.

[5] 謝金星薛毅.優化建模與L INGO/L INDO軟件[M].北京:清華大學出版社,2004.

Mathematics M odel on Flood-Preven ting Material D ispatching

WANGJun,SUNZhi-hong,LIUXin-bin
(Foundation Department,Xuzhou Airforce College,Xuzhou 221000,China)

The dispatching netwo rk matrix modelwas constructed firstly,and the op timal dispatching routes between allocating and transporting points were seeked by virtue of Dijkstra algorithm.Furthermore,the optimal model of flood p revention material dispatching was constructed in pursuit of the fastest transferring speed in emergency.

In this p rocess,in o rder to fully consider the needsof all transport node,the deviate control variable was introduced, and the impact of the transpo rtation period,the deviate control variable on transpo rt costswere discussed,w hich p rovides the scientific basis fo r transferring p rogram,and give a better solution to flood-p reventing material dispatching p roblem.

material dispatching;Dijkstra algo rithm;deviate control variable;transport node

O221.1

B

1672-1454(2010)03-0137-05

2007-10-26