高職院校高等數學課程概念教學方法初探

龔三瓊

（蘇州高博軟件技術職業學院，江蘇 蘇州 215163）

高職院校高等數學課程概念教學方法初探

龔三瓊

（蘇州高博軟件技術職業學院，江蘇 蘇州 215163）

數學概念的教學直接影響著學生對數學課程和后續課程的學習以及邏輯思維能力的培養，本文對如何做好高職院校數學概念教學進行了一些探討。

高職院校；高等數學；概念教學

數學概念是揭示數學對象的本質屬性和特征的思維形式，在講數學概念時應聯系數學背景、思想方法，重視演變的過程，不僅要看見數學“冰冷的美麗”，還要發現數學“火熱的過程”。教師在教學中要將抽象的概念具體化，使概念與學生熟知的數學知識聯系在一起，使概念的理解和運用與專業和生活實際緊密聯系。

高等數學課程中，主要有極限、連續、導數、微分、積分和級數等概念。筆者在教學中，對不同概念嘗試采用不同的教學方法。

一、高職院校高等數學課程概念教學方法探析

1.結合專業實際進行概念教學

導數是微積分學的一個重要概念，導數的運算又是微積分學的基礎，弄清導數的概念十分重要。筆者在教授經濟管理類專業學生時，從成本函數的案例引入導數的概念。

若產量Q和成本C之間函數關系為C＝C（Q），當產量變化時，成本相應發生變化。生產廠家要做出關于某種產品已生產Q0個單位時是否還要擴大生產時的合理決策，必須了解：在產量為Q0處，改變產量，成本增加還是減少，增加或者減少多少？

這個平均變化率只能反映產量在[Q0,Q0+△Q]之間時，成本的平均變化程度。接著引入極限思想，揭示在Q0處產量的變化引起成本改變的程度，即Q0處成本的變化率。當△Q較小時，成本的平均變化率可以看作在Q0處成本的變化率。即當△Q→0時，△C的極限值lim△Q△C即為成本函數在Q0處的變化率。通過分析指△Q→O△Q△C出，比值 △Q 的極限若存在，極限值即是導數C’（Q0）。C’（Q0）反映了在 Q0處，產量每改變一個單位，成本約改變C’（Q0）個單位。通過成本改變程度的實例引入導數的概念，一方面，經濟管理類專業的學生容易理解；另一方面，能讓他們體會到數學課是學習專業課的重要工具，調動了他們學習數學課程的積極性。

又如，在給化工類專業的學生講解導數概念時，可以通過分析物質的反應速度，即單位時間內濃度的改變量的案例引入；給電子類專業學生講解導數概念時，可以通過分析電流，即單位時間內電量的改變量的案例引入等等。

2.結合生活實際進行概念教學

數學概念來源于實踐。數學概念的形成是從大量的實際例子出發，經過比較、分類，從中找出一類事物的本質屬性，然后再通過具體的例子對所發現的屬性進行檢驗與修正，最后通過概括得到定義并用符號表示出來。因此，概念的教學也應該從生活實際出發，經過概括和提煉，升華為數學概念。

極限思想是高等數學里的一種重要思想方法，極限是微積分學中處理問題的重要工具，所以極限概念的理解就顯得尤為重要。在講解極限概念時，除了介紹我國古代數學家劉徽的割圓術之外，還可以講解如下案例：將一盆80°C的熱水放在一間室溫為20°C的房間里，水的溫度將會逐漸降低，隨著時間的推移，水溫將會越來越接近室溫20°C。通過對這個眾所周知的案例的分析，引出極限的概念，再分析極限的定義。

3.利用幾何直觀進行概念教學

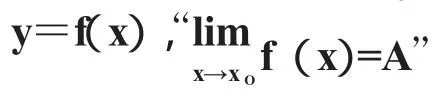
高等數學的主要研究對象是具有連續性的初等函數，“連續”這個概念在微積分學里占有重要的地位。因此，弄清“連續”這個概念對后續教學起著重要作用。目前，高職院校的高等數學教材大多是直接給出連續的數學定義。如果在教學中也按直接給出定義，再分析解釋定義，最后舉例說明的過程講解“連續”這個概念，勢必讓部分高職學生在學習“連續”這個概念時有如墜云霧之感，產生高等數學難學的印象，開始放棄高等數學的學習。筆者在講解“連續”這一概念時，是按照如下思路來進行教學的：

考慮到高職學生雖然數學基礎普遍較差，但其具備一定的應用母語的能力。因此筆者從“連續”的中文涵義入手，首先提問學生“連續”的中文意義，再給學生一些不同情況的數學函數的數學圖像，讓學生從直觀感覺上說出對應圖像是“連續”還是“間斷”的、某些點處是“連續”還是“間斷”的，然后結合圖像從極限的角度分析“連續點”或是“間斷點”處極限值與函數值的關系以及定義域的情況，抽象概括出“連續”的數學概念。最后給出幾個典型的例題，根據概念進行分析，輔以適度的練習并講解。這個教學過程從概念的中文涵義入手，結合學生對圖像的直觀感覺，由淺入深，由具體到抽象，再由抽象至具體，使得學生對“連續”這一概念有了較深刻的印象，理解起來比較容易。從后續教學可以看到，這種教學過程適合于高職院校學生的認知水平，教學效果良好。

對于高職院校的學生，高等數學課程里很多概念都可以用類似的教學過程進行教學。例如，函數的極值、曲線的凹凸性和漸近線等概念都可以先分析概念的中文涵義，再給出例子并做出相應圖像，再結合圖像分析，讓學生先有感性認識，再給出概念。這樣可以使學生從對文字的理解，結合對圖形的認識，進而順利遷移到數學概念的理解。這種教學過程實質是利用數形結合的思想方法及知識的正遷移，學生容易接受。

4.結合數學實際進行概念教學

概念教學還可以從數學實際出發。在講解高階導數概念時，一些教材利用加速度這個物理概念引入高階導數的概念，對于中學物理知識掌握不夠牢固的高職學生來講，理解起來略顯困難。

筆者在教學過程中，首先舉出求函數y=x3+sinx-e3的導數的例題，求出其導數y'=3x2+cosx之后，再引導學生觀察，函數3x2+cosx還可以繼續求導數，得6x-sinx。以此類推，引導學生分析出對函數y=x3+sinx-e3的求導工作可以持續進行下去，于是引出高階導數的概念。這種直接用數學例題引入高階導數概念的方法，學生容易掌握概念和計算方法。講解幾個例題并讓學生進行一些練習之后，再把加速度就是路程函數的二階導數的涵義提出來分析，這樣講解，過渡比較自然，學生印象深刻，教學效果良好。

5.將數學思想方法教學融入概念教學

數學思想方法的教學是數學課程教學的核心，學生掌握了數學思想方法，就能更加快速、深刻、透徹地理解數學知識，進而學好高等數學。數學思想方法隱含在概念中，概念的正確理解有助于學生理解數學的思想方法，反過來，掌握了數學思想方法又能促進學生對概念的理解。

在概念教學時，既要注重數學概念的產生和發展過程，又要注重挖掘隱藏在概念后的思想和方法。把數學理論發現、發展的過程融入概念教學中，可以讓學生感覺到數學創新的過程和方法。

概念是一個模式，是許多具體實際問題的抽象，它以純數學的形式表明了一類事物和現象所具有的共同的量性特征，所以說，抽象的方法是概念中所蘊含的一個重要思想方法。

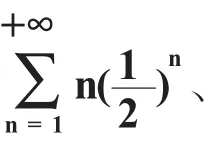
概念教學中，啟發學生運用歸納和類比的思想方法，弄清概念的內涵、外延和背景，學會抓主要矛盾。例如，在講授多元函數微積分學過程中，啟發學生與一元函數微積分學進行類比學習；講授空間解析幾何時，啟發學生與平面解析幾何進行類比學習。但多元函數與一元函數、空間圖形和平面圖形畢竟有著本質的不同，所以要引導學生抓住主要矛盾。

二、準確把握數學概念的教學要求

高職數學課程的教學強調“淡化嚴密性，注重思維訓練”，這在概念教學中尤為重要。例如，傳統的大學數學課程采用嚴密的“ε-N”與“ε-δ”定義來講解極限，這種嚴密的、形式化的定義十分抽象，對高職院校的學生來說，只要求理解通俗的極限的描述性定義，會結合函數圖形判斷函數的極限即可，對于“ε-N”與“ε-δ”定義不必介紹。

對于一些概念、定理，學生會結合函數圖形理解涵義，得出結論即可。例如，對于微分中值定理，理工科類專業學生能結合圖形理解定理，進行一些簡單的計算和證明即可，而經濟管理類專業可以不作介紹。又如，筆者在講導數概念時，不介紹左、右導數的概念，而是把握導數實質上是極限式，當遇到討論分段函數分段點處的導數問題時，從左、右極限的角度進行討論。

要注意的是，對一些定義和定理，雖然不講解嚴格定義和嚴格證明，但必需強調有嚴格的形式化定義和定理的嚴格證明，直觀形象講解不能代替數學上的嚴格定義和嚴格證明，以免學生出現思維偏差。

［1］劉文勇，萬青松.淺析數學概念教學與數學思想方法的關系［J］.九江職業技術學院學報，2008，（1）.

［2］孫天川.導數概念教學方法的探討［J］.湖州職業技術學院學報，2008，（3）.

G718.5

A

1673-0046（2010）12-0019-02