頻率選擇性信道下Turbo碼和SC-FDE的聯合方案

(1.裝備指揮技術學院 研究生管理大隊，北京 101416；2.裝備指揮技術學院 光電裝備系，北京 101416)

1 引 言

在寬帶無線通信系統中，隨著通信速率不斷提高，由多徑傳播引起的頻率選擇性衰落對通信的可靠性造成了嚴重影響，所以采用頻譜效率高的抗多徑衰落技術來提高系統性能成為解決寬帶無線通信的一個關鍵問題。單載波頻域均衡(SC-FDE)和正交頻分復用技術(OFDM)是兩種頻率效率較高且具有抗頻率選擇性衰落信道的優勢，還具有較低的復雜度[1-2]。但OFDM存在對定時誤差、載頻同步誤差比較敏感，而且具有較大的峰均功率比(PAPR)等問題，直接影響了OFDM技術更大規模的應用前景。而基于頻域均衡技術的SC-FDE有效地結合了OFDM和單載波傳輸的優點，具有較強的克服頻率選擇性衰落的能力，并克服了OFDM系統的不足[2]。Turbo碼巧妙地將卷積碼和隨機交織器結合在一起，實現隨機編碼的思想，并采用軟輸出迭代譯碼來逼近最大似然譯碼，因此它是一種編碼增益及糾錯能力很強的差錯控制編碼方法。由此，本文設計了一種基于軟輸出的SC-FDE和Turbo碼的抗頻率選擇性衰落的寬帶傳輸方案。一方面，利用SC-FDE來均衡頻率選擇性信道多徑傳播引起的符號間干擾(ISI)；另一方面，利用Turbo碼的強大糾錯能力降低信噪比門限，從而提高系統的整體性能。

2 Turbo碼編譯碼

Turbo碼[3]是在1993年國際通信會議(ICC)上首次被提出的，其編碼結構如圖1所示。它充分體現了Shannon信息論中的隨機編碼思想，隨機打亂信息序列后，用不同的分量編碼器來編碼。編碼器由兩個反饋的系統遞歸卷積碼編碼器(RSC)通過一個隨機交織器并行級聯而成，再通過刪余的方式得到不同碼率的碼字[3-4]。

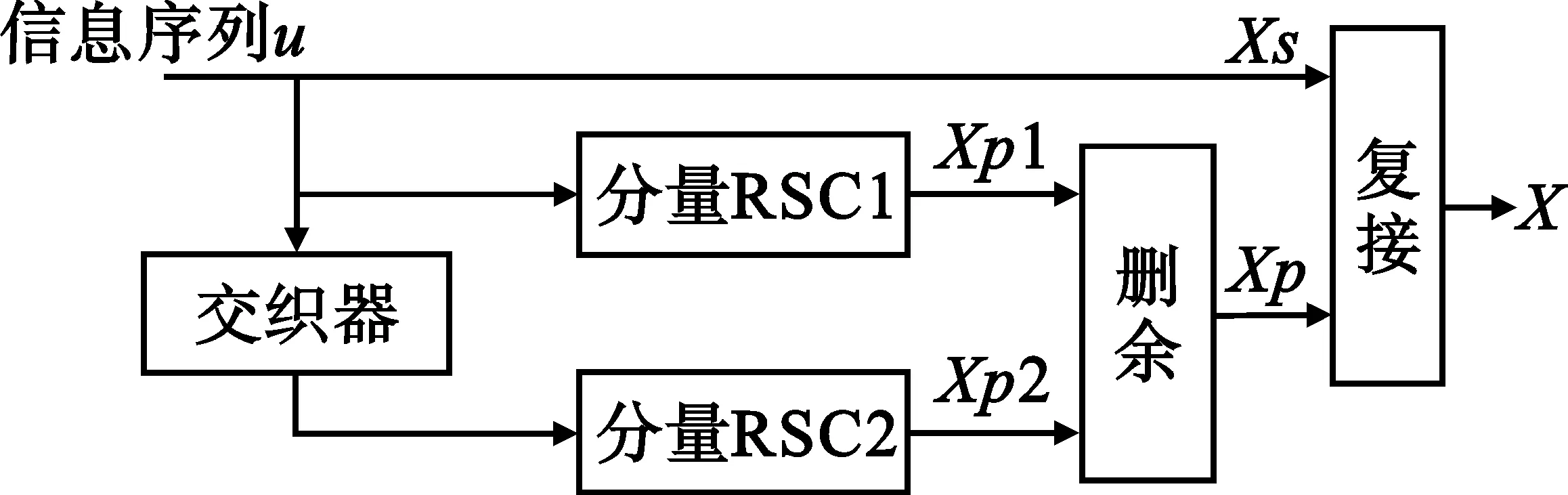
圖1 Turbo碼編碼結構圖Fig.1 The encoding structure of Turbo codes

圖2 Turbo碼譯碼結構圖Fig.2 The decoding structure of Turbo codes

3 SC-FDE基本結構及均衡方案

SC-FDE基本結構如圖3所示。在發射端，數據經過符號映射后形成幀格式，并在每個數據幀之間插入保護間隔來最大限度地消除符號間干擾，保護間隔的長度一般要大于無線信道的最大時延擴展，這樣，一個符號的多徑分量就不會對下一個數據幀造成干擾，也就是將每幀的最后Ng個符號復制到幀頭作為循環前綴(Cyclic Prefix，CP)，形成長度為N+Ng的數據塊，然后經過加入高斯白噪聲的多徑信道到達接收端。在接收端，對接收到的數據塊進行刪除循環前綴的操作，然后使用FFT將信號變換到頻域，在頻域經過均衡處理后，再通過IFFT操作變換回時域進行判決，得到重建的數據符號。

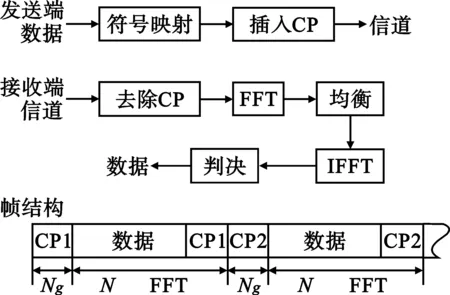
圖3 SC-FDE基本結構Fig.3 The structure of SC-FDE

設每N個映射的碼元xn組成一個傳輸數據塊，信道沖激響應為hn，令符號的碼元數小于信道沖激響應hn的長度，則每個接收到的數據符號可以表示為

yn=hn?xn+vn，n=0,1,2,…,N-1

(1)

Yk=XkHk+Vk，k=0,1,2,…,N-1

(2)

式中，Hk是信道的頻率響應。假設同步和信道估計是理想的，進行頻域均衡后：

Zk=WkYkHk+WkVk，k=0,1,2,…,N-1

(3)

式中，Wk為前饋頻域濾波器的系數。判決前的信號：

(4)

式中,P是發送信號xn的平均功率。

(5)

但是，當信道衰落很大(很小)時，上式等號右邊第二項噪聲的權重很大，對信號判決影響非常大，通常采用最小均方誤差(MMSE)均衡，則：

(6)

4 系統方案及軟信息提取方法

由第3節SC-FDE的基本結構可知，傳統的SC-FDE在頻域均衡、IFFT變換回時域后，直接硬判決，如果系統中有信道編碼模塊，那么均衡后進入信道譯碼的先驗信息實際上是硬信息(相對于軟信息)，直接硬判決實際上是降低了均衡后數據信息的精確性。而對于像Turbo碼這樣的Shannon極限碼來說，它的超強糾錯能力主要是靠分量碼交織的“隨機”性和迭代譯碼器的軟信息交換帶來的[3]，如果SC-FDE變換回時域后不直接硬判決而輸出軟信息，那么必然會帶來系統整體性能的改善。由此，得出基于軟信息輸出SC-FDE和Turbo碼的傳輸方案，如圖4所示。數據經過Turbo編碼后，再經過多徑衰落信道。假設信道輸入向量為x，則信道的輸出向量為r=ax+n，a是瑞利衰減系數。在接收端，接收向量r經過SC-FDE均衡后，通過提取比特軟信息模塊向Turbo譯碼器輸出軟信息(比特似然信息)，再經過Turbo解碼器恢復出數據。圖4中的h(t)是信道的沖激響應，n(t)是高斯加性白噪聲。

圖4 系統方案Fig.4 The scheme for the system

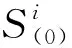
(7)

進一步得出：

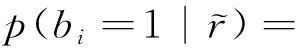
(8)

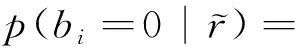
(9)

所以bi的對數似然比為

(10)

設發送數據等概，則：

(11)

其中：

(12)

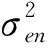
(13)

5 仿真與結果

在SUI3[8]信道下對提出方案的性能進行了Monte-Carlo仿真。具體仿真參數為：Turbo碼的碼率為1/2，碼長為1 024，隨機交織，迭代5次，生成矩陣為[1 1 1；1 0 1]，刪余矩陣為[1 0；0 1]，譯碼算法為Log-MAP；SC-FDE塊長為256，其中CP長度為32，采用MMSE均衡，QPSK調制和16QAM調制，載波頻率為2 GHz，信噪比范圍為0～6 dB，間隔為1 dB，信號點數為262 144。

圖5為SC-FDE軟輸出信息改進前后的系統在相同信噪比下的誤碼率比較，從中可以看出，信噪比下改進后系統的誤碼率要比未改進系統明顯降低，QPSK在誤碼率10-5下改進的系統相對于未改進的大約有1.8 dB增益，16QAM在誤碼率為10-4下改進的系統相對于未改進的大約有0.8 dB增益，顯示了基于軟輸出信息SC-FDE系統的優越性。

(a)QPSK

(b)16QAM圖5 相同信噪比下誤碼率比較Fig.5 The BER comparison in the same SNR

6 結束語

本文提出了一種基于軟輸出SC-FDE和Turbo碼的抗頻率選擇性衰落寬帶傳輸方案。通過在接收端的SC-FDE后增加符號軟信息輸出模塊和設計符號軟信息提取算法，提高了輸入到Turbo碼SISO譯碼器先驗信息的精確性，改善了整個系統的性能。分析和仿真表明，與傳統SC-FDE硬判決輸出相比，系統輸出信噪比得到明顯改善。本文的理論研究對系統的工程應用具有一定的參考價值，但對軟信息提取的簡化算法有待進一步研究，以提高方案的實用性。

參考文獻：

[1] Falconer D，Ariyavisirakul S L，Benyamin S，et al．Frequency domain equalization for single-carrier broadband wireless systems[J]．IEEE Communications Magazine，2002，40(4)：58-66．

[2] Sari H，Karam G，Jeanclaude I．Transmission techniques for digital terrestrial TV broadcasting[J]．IEEE Communications Magazine，1995，33(2)：10-19．

[3] Berrou C，Glavieux A，Thitimajshima P．Near Shannon limit error-correcting coding and decoding：Turbo-codes[C]//Proceedings of IEEE International Conference on Communications．Switzerland，Geneva:IEEE,1993：1064-1070．

[4] Todd K M．Error correction coding-mathematical methods and algorithms[M]．Hoboken：John Wiley & Sons，2005：584-586．

[5] WU Yu-fei．Design and implement of parallel and serial concatenated convolutional codes[D]．Blacksburg：Virginia Polytechnic Institute and State University，1999．

[6] 劉東華．Turbo碼原理與應用技術[M]．北京：電子工業出版社，2004：72-98．

LIU Dong-hua．Turbo Codes Principle and Application Techniques[M]．Beijing：Publishing House of Electronics Industry，2004：72-98．(in Chinese)

[7] 王輝，王中訓，段中華．基于AWGN多次迭代的Turbo碼與卷積碼性能比較[J].煙臺大學學報(自然科學與工程版)，2009，22(1)：46-49．

WANG Hui，WANG Zhong-xun，DUAN Zhong-hua．Capability Comparison Between Turbo Codes and Convolutional Codes in AWGN[J]．Journal of Yantai University(Natural Science and Engineering Edition),2009,22(1)：46-49．(in Chinese)

[8] IEEE 802.16.3c-01/29rl，Channel models for fixed wireless applications[S].