高等數學中配項法的應用研究

張潔萍

(山西大同大學數學與計算機科學學院，山西大同 037009)

高等數學中配項法的應用研究

張潔萍

(山西大同大學數學與計算機科學學院，山西大同 037009)

采用列舉法探討了配項法在求函數極限、不定積分和函數展開成冪級數等方面的應用，揭示了配項法在高等數學中的應用技巧，為配項法的應用提供了一種新的思路.

配項法 函數極限 不定積分 冪級數

配項法，即代數式中原本沒有某項，但是為了在求解問題的過程中利用某公式、某定理、某結論，從而將代數式加上某項然后再減去某項，或者是乘以某項再除以某項，是解題中一種目的明確的變形技巧[1-2]，有些題利用配項法甚至可以簡化計算過程.高等數學中有很多問題從形式上看讓人無處下手，但是只要能巧妙地使用配項法，就會迎刃而解，能起到事半功倍的效果.接下來從以下三方面研究配項法在高等數學中的應用.

1 配項法在函數極限中的應用

配項法在函數極限中的應用并不陌生，比如用ε-δ語言定義證明，就需要通過適當的配項，設法在式子中保留｜x-x0｜，以利用｜x-x0｜<δ來得到｜f(x)-A｜<ε的結論.此外，配項法在函數極限的一些證明題和求解函數極限的問題中也有巧妙的應用[3-4],下面舉例加以說明.

分析：本題前后兩式形式差異不大，經過觀察分析，通過應用配項法使兩式聯系起來，則很容易使本題得證.

證明先證充分性：

應用配項法可得到如下等式：

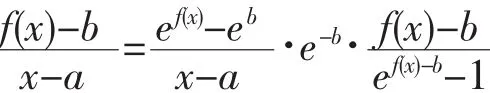
所以

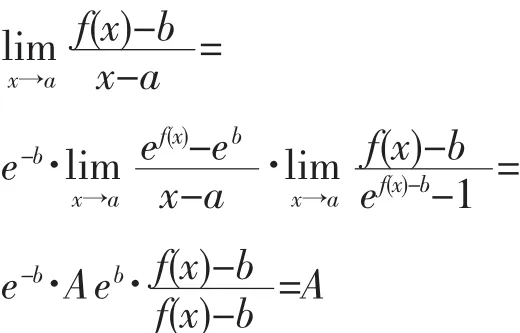
再證必要性：

應用配項法可得到：

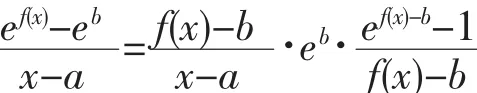
所以

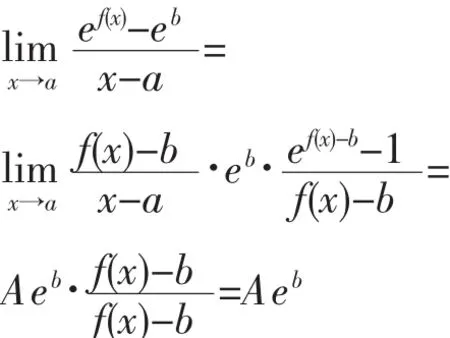
分析：本題中的函數比較復雜，無法利用函數連續性以及極限的四則運算法則等來求解，但是觀察到,這樣對乘除配項，使之向兩個重要極限的形式轉化，再進一步求其極限.

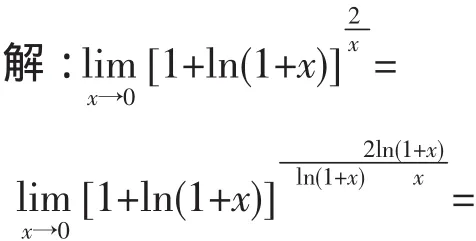
2 配項法在求不定積分中的應用

求不定積分的方法主要有換元法和分部積分法.在計算過程中，這些方法往往需要和配項法相結合，使所求不定積分化為基本積分公式型積分，從而使問題簡化[5].

分析：根據被積函數的形式，若要湊成ex的微分，則要對被積函數乘除配項，即被積函數乘以ex，再除以ex.

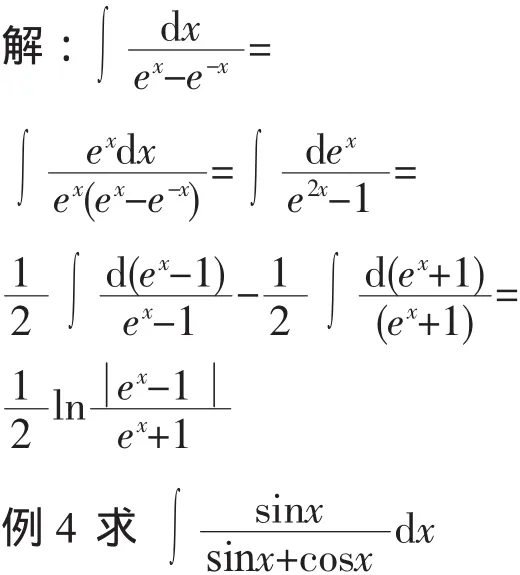
分析：本題是關于三角函數有理式的積分，可以利用代換使之轉化為有理函數的積分，雖然可進一步求得其解，但是計算過程比較繁瑣，重新審視被積函數，如果將分子應用配項法使之湊成分母和分母導數的線性組合，則可以很容易求得其解.

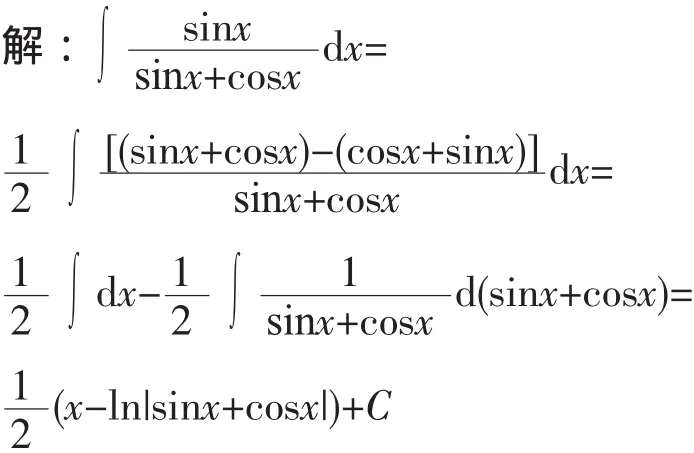
3 配項法在函數展開成冪級數中的應用

函數展開成冪級數的方法有直接法和間接法，用直接法將函數展開成冪級數計算量很大，所以通常我們用間接法將函數展開成冪級數，也就是根據已經證實的函數展開式，獲得所求函數的展開式.這就需要對所給函數進行配項，使之轉化成已經證實的函數[6-7].

而

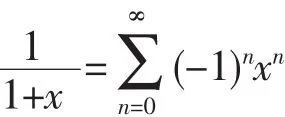
所以有

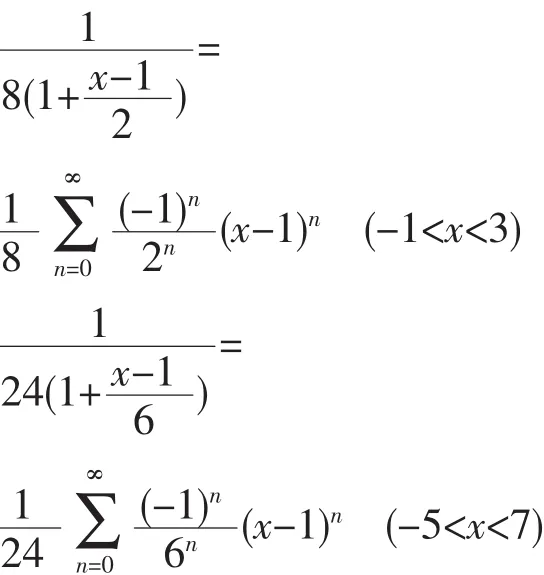
得到

分析：觀察本題中f(x)的結構特點，我們想到用乘除配項法來使f(x)轉化為有利于求解的結構形式，即f(x)乘以(1-x2)再除以(1-x2)，進而利用 1 1-x=來求解.

解：當｜x｜≠1時，應用配項法可得到

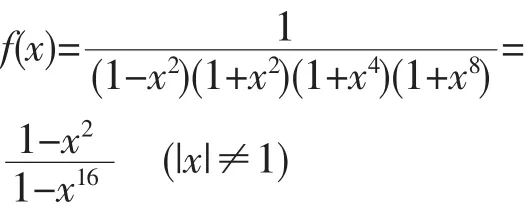
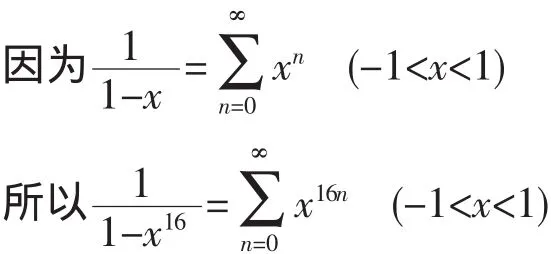
從而可得到

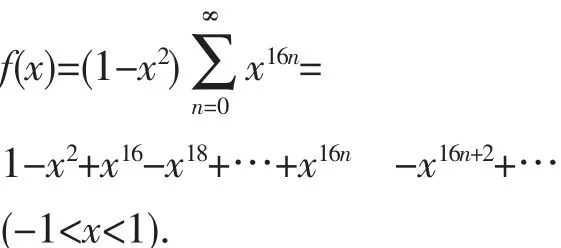
4 結語

本文列舉了配項法在求函數極限、不定積分和函數展開成冪級數中的應用，其實配項法的應用貫穿于整個高等數學的內容中[8-10]，面對眾多原本復雜的問題，恰當使用配項法，可以巧妙地將其解答，從這點看，熟練掌握配項法在高等數學的學習中顯得尤為重要.

[1]李曉萍.配項與湊微分法的巧妙應用[J].高等數學研究,2006,9(1):49-51.

[2]錢昌本.高等數學解題過程的分析和研究[M].北京:科學出版社,1994:133-139.

[3]宋硯.求極限的常用方法[J].內蒙古民族大學學報,2008,14(2):4-5.

[4]常敏慧.無窮小量在微積分中的作用[J].山西大同大學學報:自然科學版,2008,24(2):15-16.

[5]張霞.一類有理函數積分的簡單方法[J].中國科技信息,2009(23):56.

[6]高宗升,孫道椿,王敏.關于兩類冪級數系數的重排[J].數學物理學報,2002,22 A(1):91-98.

[7]方漢銘.關于一個函數展開成冪級數的若干解法[J].高等數學研究,2006,9(3):43-46.

[8]張建元.復變函數的K-積分[J].云南師范大學學報,2009,29(1):28-32.

[9]楊必成.一個反向的Hardy-Hilbert積分不等式[J].吉林大學學報,2004,42(4):489-493.

[10]劉華.關于變上限積分所確定的復合函數的若干性質與應用探討[J].齊齊哈爾大學學報,2010,26(1):81-84.

Abstract:This paper,studying application of matching item in limit of function,indefinite integral and positive series by using listing technique in this paper,presents the acrobatics about the application of matching item,and offers the new thinking in the application of matching item.

Key words:matching item;limit of function;indefinite integral;positive series

〔編輯 高海〕

A Study on the Application of Matching Item in Higher Mathematics

ZHANG Jie-ping
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

O13

A

1674-0874(2010)05-0013-03

2010-06-06

張潔萍(1982-)，女，山西定襄人，碩士，助教，研究方向：應用數學.