時間模上一階非線性邊值問題的三個正解
張 英,喬世東
(山西大同大學數(shù)學與計算機科學學院,山西大同037009)
時間模上一階非線性邊值問題的三個正解
張 英,喬世東
(山西大同大學數(shù)學與計算機科學學院,山西大同037009)
運用Legget-Williams不動點定理,在錐上討論一階非線性兩點邊值問題至少有三個正解的存在性問題.
正解 邊值問題 不動點定理 時間模 錐
在2005年,J.P.Sun和W.T.Li[1]運用錐上的不動點定理研究了邊值問題(1)當β=1時至少有一個正解;在2008年,Jian-Ping Sun[2]利用Avery和Henderson兩解不動點定理研究了邊值問題(1)至少有兩個正解;本文在錐上運用Legget-Williams不動點定理,討論時間模上的一階非線性邊值問題
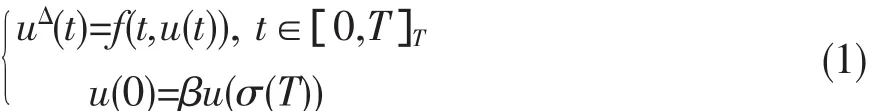
至少有三個正解.另外,我們還假設以下的條件成立:
(A)f∶[0,T]×[0,∞)T→[0,∞)是連續(xù)的且0<β<1.
1 預備知識
下面我們給出幾個引理.這些引理基于下面的線性邊值問題

引理1設0<β<1,y∈Crd[0,σ(T)],則邊值問題(2)有唯一的解
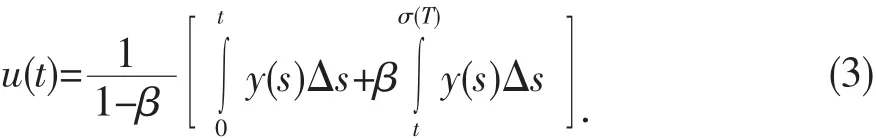
證明 因uΔ(t)=y(t),從0到t積分后有u(t)=u(0)+.利用邊值條件u(0)=βu(σ(T)),可得到u(t)=
而
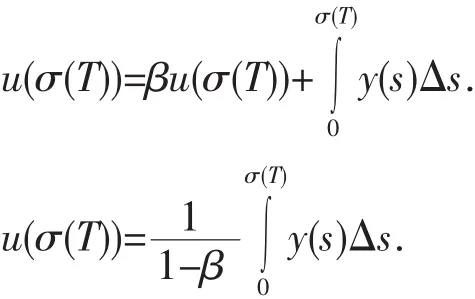
故
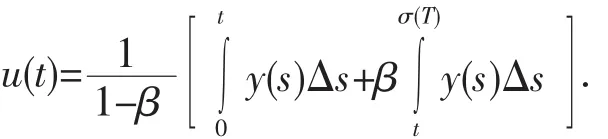
引理2設0<β<1,y∈Crd[0,σ(T)],則方程(2)的解u(t)滿足u(t)≥0,t∈[0,T]T.
我們令E=Crd[0,σ(T)]是一個巴拿赫空間,其上泛數(shù)定義為定義一個錐P?E
P={u∈E∶u(t)≥0,增加的和u(0)=βu(σ(T))

引理3[3]設u∈P則u(t)≥β‖u‖,

證明 令x(t)=u(t)-β‖u‖,t∈[0,σ(T)]T.因為xΔ(t)>0,則可知x(t)在t∈[0,σ(T)]T上是增加的,又
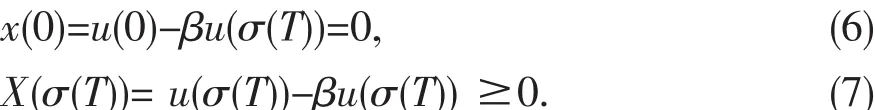
由(6)和(7)可得到x(t)=u(t)-β‖u‖≥0,即u(t)≥β‖u‖.
2 解的存在性
定理1[4]設p是實巴拿赫空間E的一個錐,集合
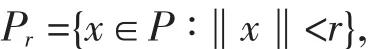


且Ψ(Φu)>q對所有的u∈P(Ψ,q,l);
(2)當‖u‖≤p時,有‖Φu‖≤p;
(3)當u∈P(Ψ,q,r)時,Ψ(Φu)>q且‖Φu‖>l,則Φ至少有三個不動點u1,u2,和u3∈滿足‖u1‖
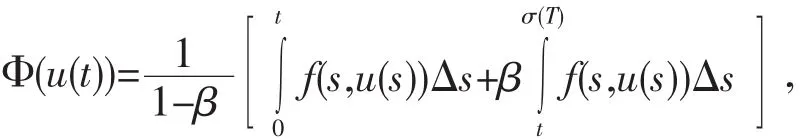
其中u∈P,t∈[0,T]T,
對于u∈P,t∈[0,T]T易知(Φu)(t)滿足方程(1).因此, P中的每個不動點y滿足方程(1).
另外,當u∈P,t∈[0,T]T,(Φu)Δ(t)≥0知(Φu)(t)是增加的,這意味著ΦP?P.故Φ是全連續(xù)的.因此,找方程(1)的解就等價于找錐P中的不動點y.
定理2[5]設條件(A)成立,又設存在常數(shù)0 則邊值問題(1)至少有三個正解u1,u2,,u3滿足u1(t) 證明驗證定理1的所有條件都滿足.定義非負連續(xù)的凹函數(shù) Ψ∶P→[0,∞)滿足Ψ(u)=u(h), P的定義如(4),我們有Ψ(u)≤‖u‖,u∈P,t∈[0, σ(T)].設y∈,則‖u‖≤c,由假設 (C1)f(s,u)≤當0≤u≤c這時有 因此,我們有 對 從而定理1的條件(1)滿足. 從而定理1的條件(2)滿足. 從而定理1的條件(3)滿足. 由于定理1的所有條件都被滿足,所以邊值問題(1)至少有三個正解u1,u2,u3,當u3(t) [1]Sun J P,Li W T.Positive Solutions for System of Nonlinear First-Order PBVPs on Time Scales[J].Nonlinear Anal,2005,62:131-139. [2]Jian Ping Sun.Twin Positive Solutions of Nonlinear First-Order Boundary Value Problems on Time Scales[J].Nonlinear Anal.,2008, 68:1754-1758. [3]Ismail Yaslan.Existence of Positive Solutions for Nonlinear Three-point Boundary Value Problems on Time Scales[J].J Comput Appl Math,2007,206:888-897. [4]Legget R W,Williams L R.Multiple Positive Fixed Points of Nonlinear Operators on Ordered Banach Spaces[J].Indiana Univ Math J,1979,28:673-688. [5]Jian Ping Sun,Wan-Tong Li.Existence of solutions to nonlinear first-order PBVPs on time scales[J].Nonlinear Anal,2007,67:883-888. Abstract:In this paper,by means of the Legget-Williams fixed point theorems in cones,we study the existence of at least three positive solutions of a nonlinear second-order boundary value problem on time scales. Key words:positive solution;boundary value problem;fixed point theorem;time scales;cone 〔編輯 高海〕 Existence of Positive Solutions to Nonlinear First-order Boundary Value Problems on Time Scales ZHANG Ying,QIAO Shi-dong O175.14 A 1674-0874(2010)05-0001-02 2010-03-02 山西省高校科技研究開發(fā)項目[200811043] 張英(1964-),女,山西大同人,碩士,教授,研究方向:常微分方程.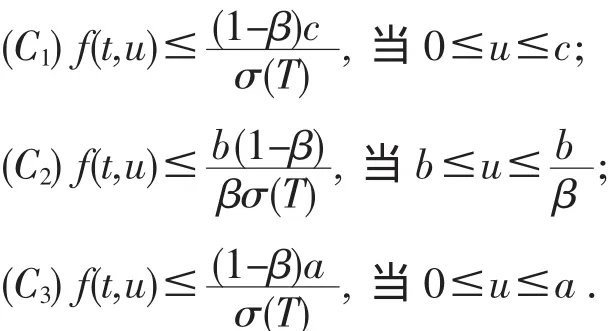
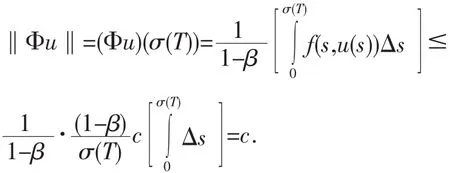

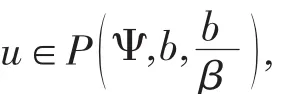
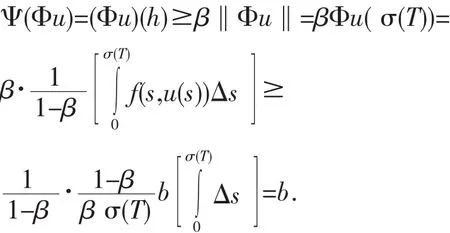
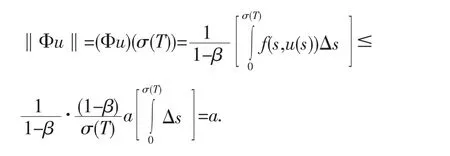
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

