關于眼科病床安排模型的幾個評價指標

王蘭卿,宋海竟

(1.山西大同大學數學與計算機科學學院,山西大同037009; 2.中北大學經濟與管理學院,山西太原030051)

關于眼科病床安排模型的幾個評價指標

王蘭卿1,宋海竟2

(1.山西大同大學數學與計算機科學學院,山西大同037009; 2.中北大學經濟與管理學院,山西太原030051)

首先引入三個重要的評價指標：病床周轉率、入院平均等待時間、入院公平度.其次，一方面通過引入虛擬病床使得整個就醫流程時間大大縮短，提高了病床的循環利用率（即病床周轉率）；另一方面利用0－1規劃更好地確定了最優入院時間，使得入院公平度較高，而且在所建的兩個模型中，均可實現病人一入院即可進行手術，從而使入院等待時間減少為0d.

病床周轉率 公平度 擬病床

根據醫療改革堅持以人為本的原則，醫院應盡量提高病床周轉率，使病床床位盡可能地滿足醫療需求.這樣不但可以提高病人對醫院的滿意度，還能使醫院本身的資源利用達到最大化.那么在醫院現有的條件下（即病床數固定），如何實現病床的高效利用以及減少病人的等待時間有著非常重要的實際意義.

目前眼科的現狀是等待入院的隊伍越來越長，且病床的周轉率不高.我們知道患者來到醫院尋求服務，而醫院的醫療資源有限，二者之間發生沖突時，就會產生排隊現象.如果患者排隊時間過長，超過他們的承受極限，必將會導致患者的流失，給醫院造成一定的損失，同時也可能會影響患者的診斷和救治，造成醫療事故.故我們認為，每個醫院在今后的發展與壯大中，都應堅定不移地貫徹醫改精神.本模型的建立，目的就在于堅持以人為本的前提下，利用虛擬病床或0－1規劃更好地解決醫院排隊過長的問題.

1 模型的基本假設和基本概念

1.1 模型的基本假設

首先，為討論方便，我們作如下假設：病人無性別限制；病人之間互不影響，不同種類的病人可住同一病房；病人無復診，即一次性治好；手術條件無限制；每天到醫院就診的每類病人的比例確定；再不相重疊的時間區間內，到達醫院就診的病人數是相對獨立的.其次，我們依次設外傷、視網膜疾病、白內障單眼、白內障雙眼、青光眼分別為第1、2、3、4、5類；Pi、Ri和Ei（i＝1，2，3，4，5）分別表示第i類病人所占的比例、第i類病人一周內的入院人數和在最優入院時間內每天第i類病人的入院人數；N表示該院眼科平均每天的出院人數.

1.2 基本概念

定義1虛擬病床:在該眼科科室沒有病床床位,手術條件又無限制的情況下,每位病人就診后對其按照最大公平度進行編號,然后按編號安排給病人一個虛擬的“床位”.

注:虛擬病床并不是一個真實的床位,僅僅是一個確定了入院手術時間的編號,病人在得知手術時間后回到家中居住,形式上占用了病床.

定義2平均逗留時間：指一個被服務者在系統中停留的平均時間.逗留時間＝等待時間＋服務時間.

2 評價指標和模型的建立

2.1 評價指標

下面將討論病床安排優劣的評價指標體系.主要有以下幾種：①病床周轉率；②入院平均等待時間；③入院公平度；④病床使用率；⑤病床周轉次數；⑥平均住院日（即平均占用病床時間）；⑦門診診斷與出院診斷符合率；⑧單病種平均醫療費用.

由于在所給模型中病人足夠多，醫療條件充分，不會出現空床現象，故病床使用率為100%，因此與費用和符合率沒有多大關系.而建立該模型的目的在于解決排隊過長的現象，以提高對醫院資源的有效利用，即應使病床周轉率盡可能大，一定時間區間內病床周轉次數和就醫的人數盡可能多.另外，要使現在排隊等待入院的病人盡早地入院，則應減少入院前的等待時間.同時在FCFS（即先到先服務）的前提下，還應滿足各種病人入院后所占的比重與入院前的比重相同，使之達到最公平狀態.因而病床循環利用率越大，等待時間越小，公平度越高，則模型越優.既然其它的各項評價指標相對于該模型而言與建模目標關系不大，只作為輔助條件，故評價該病床安排模型的優劣只需以下三個指標：病床周轉率、入院平均等待時間、入院公平度.

2.2 建立病床安排模型

要建立合理的病床安排模型，主要目的在于解決該眼科等待入院隊伍越來越長的問題，故要求每一位病人在系統內的平均逗留時間最小，醫院在每一段時間區間內使盡可能多的病人就醫，病床的循環利用率達到最大，并使入院的公平度達到最高，即可達到最優.由醫學常識可知，在整個就醫流程中，手術時間與術后觀察時間必不可少，要使得在系統內的時間達到最小，只能從就診到入院這段時間及入院到手術這段時間來進行優化.現階段該眼科從就診到手術的平均時間為15 d，占了整個就醫流程的很大一部分，使得該眼科等待入院的病人隊伍越來越長.這里我們提出了“虛擬病床床位安排”模型.根據目前該科室只有79張病床，故虛擬編號應從80開始，編號按照FCFS（即先到先入院）的方法進行.在滿足公平度最大的前提下，我們對已編號的病人有以下兩種方案：

2.2.1 模型1

只限于該眼科科室內考慮，由于床位一定，故這種方案所指的虛擬病床并不是一個真實的床位，而是一個假想的床位，僅僅是名義上已經入院了.醫院可根據現有的病床床位的實際使用情況安排病人的手術時間，病人在得知手術時間后回到家中居住，等到了約定的時間再到醫院進行手術，而在病人等待手術的這段時間內醫院應為其做好手術準備工作，使得病人一入院就能手術，手術前不再占用病床，這樣整個就醫流程就只包含手術時間和術后觀察時間，使入院等待時間減少為0 d.

2.2.2 模型2

從整個醫院的資源利用來考慮，由于病床的利用率一般不可能達到100%，有的科室總是人滿為患，而有的科室卻是門可羅雀，故可以考慮把人較多的科室的病人向其它病人較少的科室轉移，打破科室之間的界限，使病床分配從整個醫院來考慮，提高醫院的資源利用率.這樣該虛擬的病床是真實的床位，只不過是其它科室的床位而已.病人得到編號后，若該眼科的病床都已住滿，即可安排到其它有空余病床的科室.由于除了外傷外，其余眼科疾病很少有急診，直接可提前進行手術準備，而手術條件又不受限制，故只要準備充分，可即刻進行手術，即只要入院就可進行手術（實際生活中可以給適當的準備時間，此處為了簡便，故使等待時間為0 d）.從就診到手術的時間減少為0d，沒有病人占用病床，使得整個就醫流程大大減少，病床這樣虛擬后，病人排隊等待床位、睡加床的現象也將得到很大的改善，醫院資源的有效利用率也將大大提高.

虛擬病床安排模型的使用，使得從就診到手術占用病床時間為0 d，并且病人一就診就住院，這樣不但提高了醫院的病床周轉率，而且使病人減少了一部分因住院而帶來的經濟負擔.另外，從心理學的角度來說，對于該模型，病人也是樂于接受的.該模型的建立，也體現了現代醫療改革的主旨：“以人為本.”但方案一不適用于急診與突發險情概率較高的病例，方案二更接近現實一些.

對于病人入院的最優時間安排，為了使之達到相對的公平，即要使之滿足FCFS，又要滿足在一個時間區間內入院的各種病人數與各種病人所占比例相符（這里取1周為一個時間區間）.目前該科室每天平均出院人數N＝8.現應用0－1規劃對入院時間進行優化，引入變量Xi＝0，1（i＝1，2，3，4，5），其中0表示第i類病人的非最優入院時間，1表示第i類病人的最優入院時間，故1周的最優入院總人數為顯然其不大于7N.

由于在虛擬模型中，不論是哪種病，手術準備都是在病人入院前就做好了，病人入院即可手術，從就診到手術的等待時間為0 d，所以入院時間即是手術時間；白內障手術較簡單，且沒有急癥，故對白內障入院日加以限制，該眼科科室只在周一、周三安排入院做白內障手術，故各種病的最佳入院時間分布見表1所示.

由于外傷是只要有空余病床就可入院，并隨即準備手術，情形較特殊，故在此只對其他幾類病人作入院安排.既然在1周內出院人數為7N，則可推算出下1周的出院人數也為7N，故平均每天安排入院的人數為N.對前286位病人統計得各類病人所占的比例為：

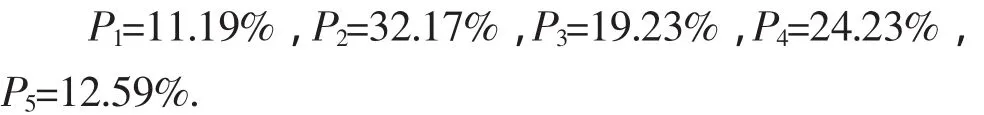
則1周內入院的各種病人人數為：Ri＝7NPi，（i＝1，2，3，4，5）.

因而在1周內入院病人的公平度比較高，每天的入院人數也可相應地確定，由上面的最優入院時間分布表我們可得以下結論

這樣只需求出平均每天的出院人數N，代入相應的公式，即可得出每天各類病人入院的具體人數.

由于運用虛擬病床安排模型，使得整個占用床位時間為手術到出院，該段時間的平均值為6 d，故過6 d后，出院人數會相應增加，打破現有的動態平衡，直到達到新的動態平衡（在未用虛擬病床安排模型優化處理之前就是一個動態平衡，平均每天出院8人，入院8人），新的動態平衡只有在現階段已入院的病人全部出院后才會形成.故每天平均出院人數是一個變量，當該值變化時，再用上述方法迭代求解即可.

3 利用指標體系對模型進行評價

3.1 對模型1的評價

由前面討論可知，對于該模型，可以用病床周轉率、等待時間、公平度這三個評價指標體系進行評價：

1）由于現階段的在系統內的時間只有手術時間和術后觀察時間，已達到最短，因而在一個時間區間內接待的病人能達到最多，故病床周轉率達到最大.

2）由于等待入院時間在該模型為0 d，而先前平均為12 d，這樣等待時間達到最小.

3）第1、2、3、4、5類病人入院人數比例與P1、P2、P3、P4、P5相符，達到了相對公平.故由以上三條指標評價可得，該模型達到最優.

3.2 對模型2的評價

對于虛擬病床安排模型，無論是方案一還是方案二，在現實生活中都有較大的相似之處，與現實比較接近，對于醫院病床安排來說，是個很實用的模型.尤其是方案二，打破了個科室之間的界限，使得醫院的整體資源利用更加充分，同時科與科之間的界限被打破，使得一個科室的護士不僅要懂得本科室的護理，而且要懂得其他科室的護理，逼著她們向“全科護士”發展，變以往的從屬被動為主動，對于整個醫院是有利的.若為了管理便利，不想打破科與科之間的界限，方案一則是一個很好的選擇，使得病人一就診就“入院”（得到一個虛擬的病床號）并知道手術的確切時間，真正入院就可進行手術，使得在等待手術的這段時間內不占用病床，這不但大大提高了醫院病床的循環利用率，而且還為病人減輕了不少的經濟負擔，從心理上來說病人是比較樂于接受的.

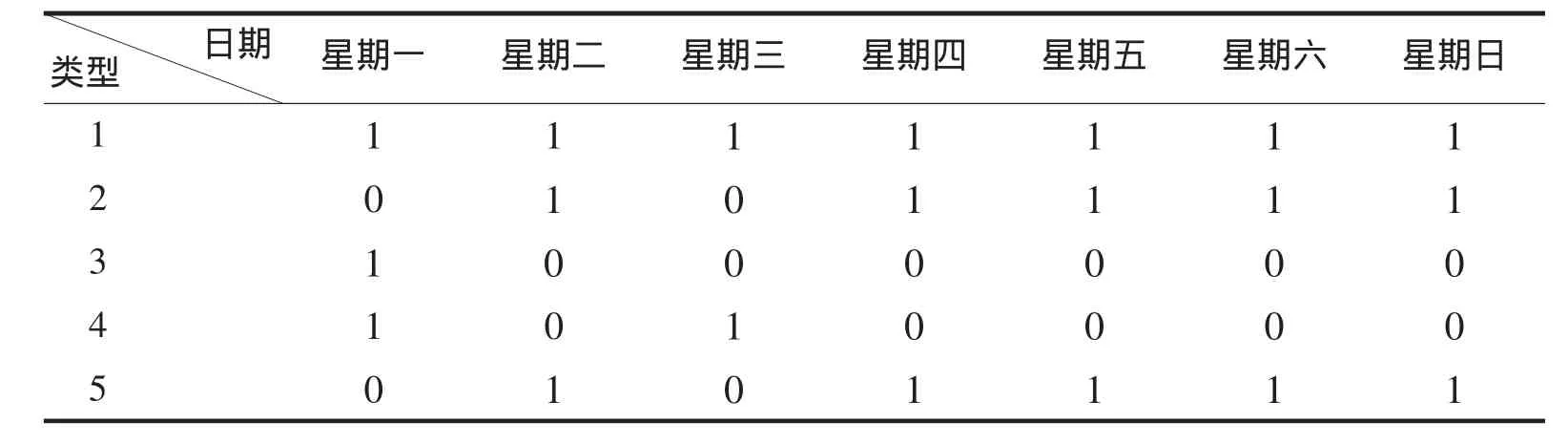
表1 各種病的最佳入院時間分布

[1]吳希.醫院門診系統的排隊過程模型[J].交流園地,2007,4(25):131-132.

[2]蔡鎖章.數學建模原理與方法[M].北京:海洋出版社,2000.

[3]胡運權.運籌學基礎及應用[M].北京:高等教育出版社,2008.

Abstract：Firstly，this paper introduces three important indices：hospital bed turnover，average hospital waiting time and fair degree.Secondly，on one hand it makes the whole medical process take much less time by introducing virtual bed，increasing the recycling rate of hospital beds （i.e.bed turnover rate）；On the other hand，it better defines the optimal admission time by using 0－1 programming，making the fair degree of hospital admission high，and in two models it can be achieved that the patient will have an operation when coming into hospitals，so that hospital waiting time is reduced to 0.

Key words：bed turnover rate；fair degree；virtual beds

〔編輯 楊德兵〕

Evaluation Indices and Models of a Hospital＇s Bed Arrangement of Ophthalmology

WANG Lan－qing1，SONG Hai－jing2

（1.School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009；2.College of Economics and Management，North University of China，Taiyuan Shanxi，030051）

TD853

A

1674-0874(2010)05-0054-04

2010－05－28

王蘭卿（1963－），女，山西太原人，副教授，研究方向：數學教育.