例談算兩次思想在組合學中的應用

●許康華 (富陽市第二中學 浙江富陽 311400) ●何文明 (富陽中學 浙江富陽 311400)

設 A={a1，a2，…，am}，B={b1，b2，…，bn}是 2個有限集合，集合{(ai，bj)|1≤i≤m，1≤j≤n}，叫做集合A與B的笛卡爾乘積，并記為A×B.

設S是A×B的一個子集，我們可用2種方法計算|S|.

對于給定的ai∈A，S中所有含有 ai的對子(ai，b)的集合記為 S(ai，·).顯然，當 ai≠aj時，S(ai，·)∩S(aj，·)= φ，

且 S=S(a1，·)∪S(a2，·)∪…∪S(am，·)，因此

另一方面，對于給定的bj∈B，定義S(·，bj)為S中所有含有bj的對子(a，bj)的集合，同理有

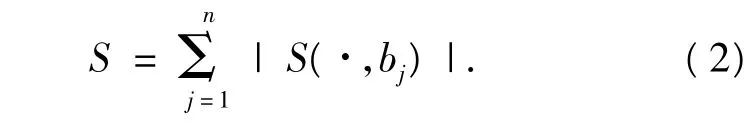
由式(1)，式(2)，得

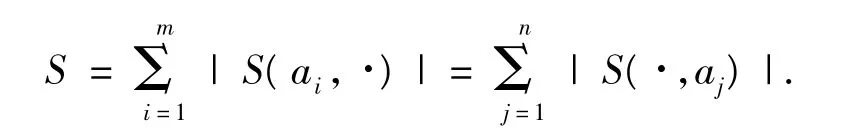
這個等式叫做富比尼(Fubini)原理，又叫做算兩次原理.

本文主要介紹用算兩次的方法來解決組合數中的一些競賽題：對同一對象從2種不同的角度去進行計算，從而尋找到解決問題的途徑.在算兩次中，常要考慮的計算對象有：數、點、元素、交點、對子、子集等.

例1 一所大學有10 001名學生，一些學生一起參加并成立了幾個俱樂部(一個學生可以屬于不同的俱樂部)，有些俱樂部一起加入并成立了幾個社團(一個俱樂部可以屬于不同的社團).已知共有k個社團，假設滿足下列條件：

(1)每一對學生(即任意2個學生)都恰屬于一個俱樂部;

(2)對于每個學生和每個社團，這個學生恰屬于這個社團的一個俱樂部;

(3)每個俱樂部有奇數個學生，且有2m+1個學生的俱樂部恰屬于m個社團，其中m是正整數，求k的所有可能值.

(2004年第45屆IMO預選題)

解用n代替10 001，a，R，S分別表示一個學生、一個俱樂部和一個社團，我們稱滿足a∈R，R∈S的有序三元組(a，R，S)為“可接受的”.

固定一個學生a和一個社團S，由條件(2)，可知有唯一的俱樂部R，使得(a，R，s)是可接受的三元組.又因為有序二元組(a，S)有nk種取法，所以可接受的三元組共有nk個.

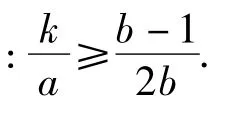
(1998年第39屆IMO試題)

證明如果2個裁判對某個參賽者有相同的評判，我們稱其為一個“對子”.

一方面，著眼于裁判：由題設，任意2個裁判最多對k個參賽者有相同的評判，即任意2個裁判最多產生k個“對子”，可得

“對子”的總數≤kC2b.

另一方面，著眼于參賽者：對任意一個參賽者，設有A個裁判判他通過，而B個裁判判他不及格，其中A+B=b.則對于這個參賽者，有關他的“對子”個數為

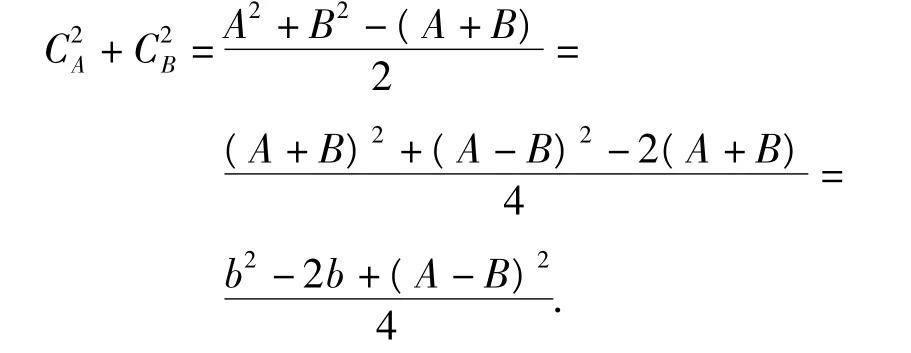
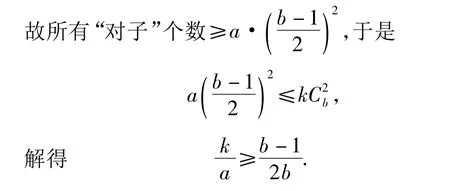
例3 設A是一個有n個元素的集合，A的m個子集 A1，A2，…，Am兩兩互不包含，試證：

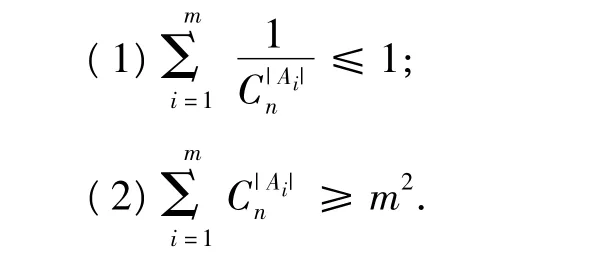
(1993年全國高中數學聯賽試題)

一方面，將A的n個元素作全排列，其不同的排列總數有n!個.

另一方面，將子集Ai的|Ai|個元素排在前|Ai|個位置，子集Ai的余集的元素排在后n-|Ai|個位置，即成排列

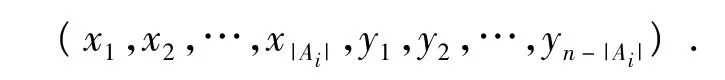
這樣的排列共有|Ai|!(n-|Ai|)!個，它們全包含在全排列數n!中.

以下只要說明，以 m個集合 A1，A2，…，Am中的元素排在前面，它們的對應余集中的元素排在后面的各個排列之間，在題設條件之下，沒有2個是相同的.

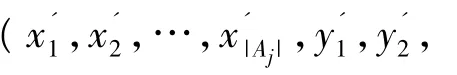
這就證明了結論(1).

注：本題源自著名的 Sperner定理(Sperner，1928)：

當然這一切，我都沒有告訴黃玲。我們時常一起上班，一起下班走那段昏暗的小巷子。旁邊的大樓都已經竣工，這使我想起那次被搶劫的遭遇，對黃玲說，其實如果那天你不出現，我就撒手了，他們只是兩個月沒領到工資的民工，不是什么壞人。

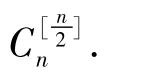
關于Sperner定理及其推廣，可參見單墫教授的《集合及其子集》.

例4 有n個人，已知他們中的任意2個人至多通電話1次，他們中的任意n-2個人之間通電話的總次數相等，都是3k次，其中k是自然數.求n的所有可能值.

(2000年全國高中數學聯賽試題)

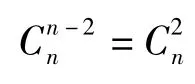
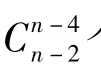
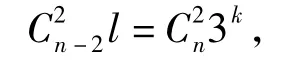
其中l為自然數，即

例5 一群科學家在一個研究所工作.在某天的8小時工作時間內，每個科學家都至少去過一次咖啡廳.已知對于每2個科學家，恰有他們中的一個出現在咖啡廳中的時間總和至少為x(x＞4)小時.求出在研究所中工作的科學家人數的最大可能值(依賴于x).

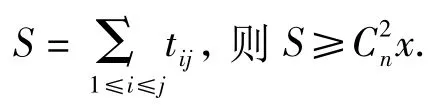
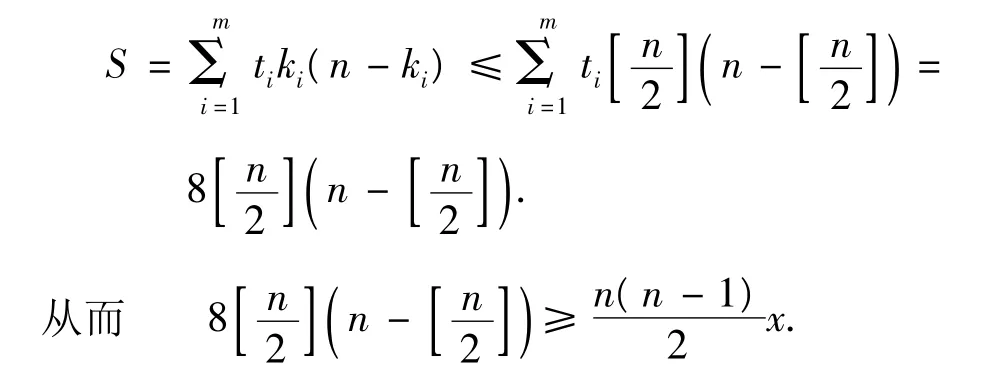
若 n 為偶數，n=2l，則

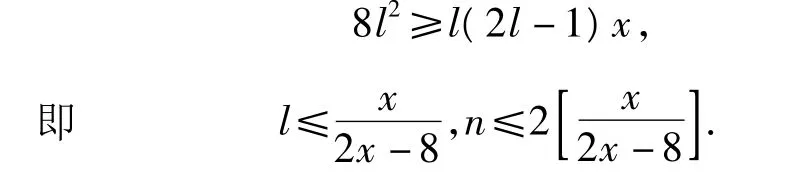
若 n為奇數，n=2l+1，則

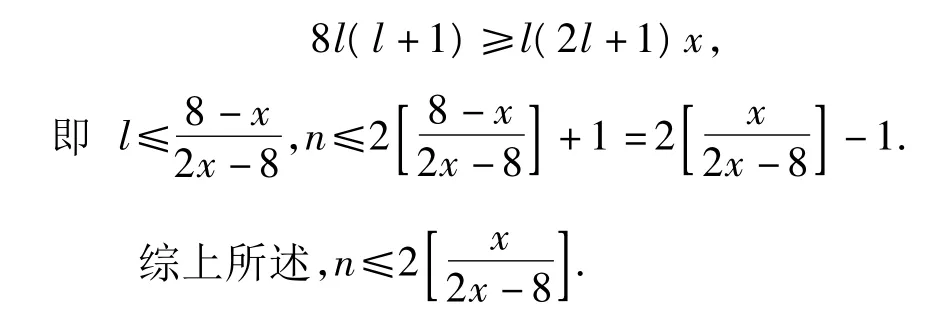
下面舉例說明不等式可以取到等號.

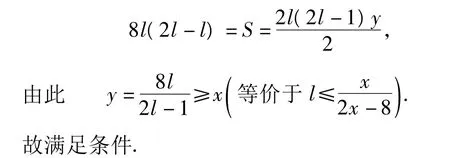
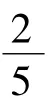
(2005年第46屆IMO試題)

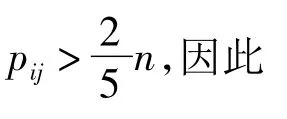
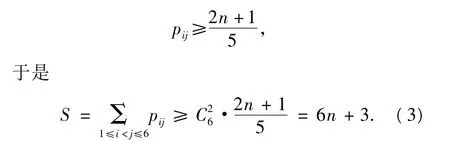
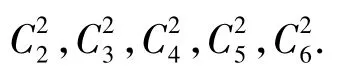
若記nr(0≤r≤6)為恰好答對r道試題的參賽者的人數，則

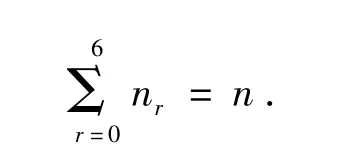
考慮到對于一個恰好答對r道試題的參賽者，他對式(3)中的和S的貢獻為(當 r＜2時，=0)，所以

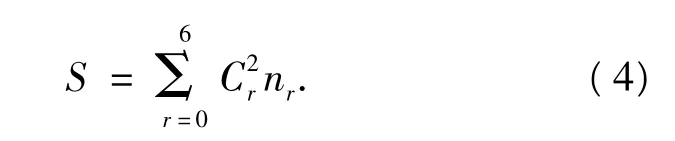
由式(3)，式(4)，可得

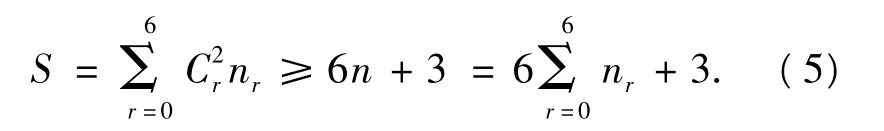
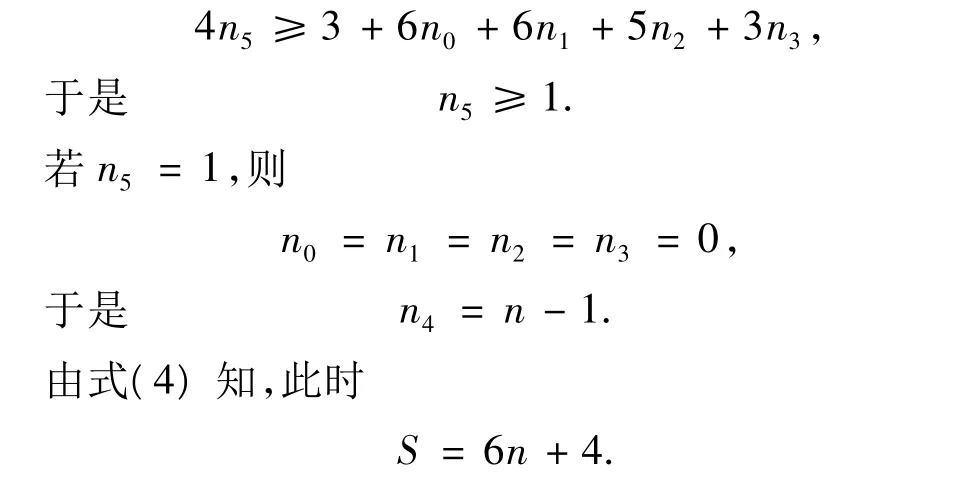
由題設，得n6=0，因此式(5)為此這些pij不可能全相等.于是，其中有14個為λ，1個為λ+1.

設(i0，j0)，使得pi0j0=λ+1.答對5道題的參賽者稱為“優勝者”.

不失一般性，不妨設優勝者沒有答對第6題，且 i0，j0不為 1，于是

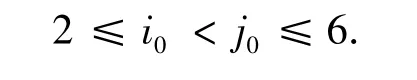
考慮和式

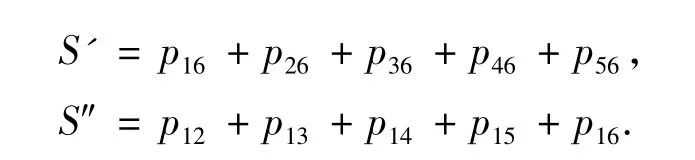
因為除優勝者外每個參賽者都恰好答對了4題，所以若有x個參賽者答對了第6題，則他們中的每一個對S'的貢獻是3;有y個參賽者答對了第1題(除優勝者外)，他們中的每一個對S″的貢獻為3，而優勝者對S″的貢獻為4，于是

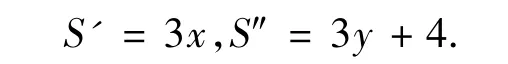
而pi0j0不在S″中出現，所以

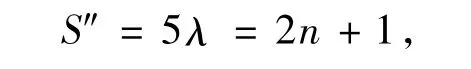
故S'為5λ 或5λ +1.從而