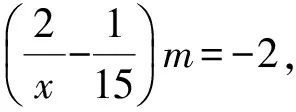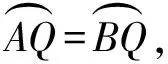2010年全國初中數學聯賽模擬卷

1．已知：在△ABC中，∠ACB=90°，∠ABC=15°，AC=1，則BC的長為

( )

( )

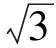
A.二者均為有理數 B.二者均為無理數

C.一個為無理數，另一個為有理數 D.以上3種情況均有可能

3．已知動點P在邊長為2的正方形ABCD的邊上沿著A-B-C-D運動，x表示點P由點A出發所經過的路程，y表示△APD的面積，則y和x的函數關系的圖像大致為

( )

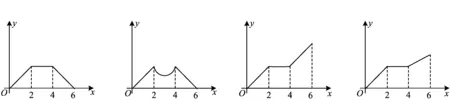
A. B. C. D.

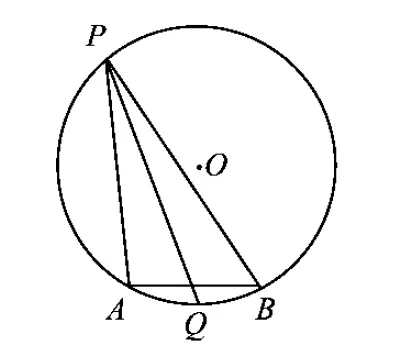
4．已知二次函數y=ax2+c,且當x=1時，-4≤y≤-1，當x=2時,-1≤y≤5，則當x=3時，y的取值范圍是

( )

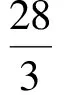
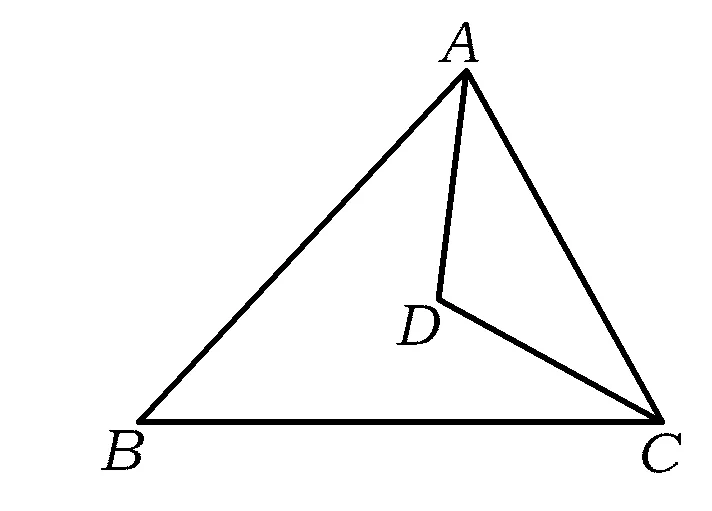
圖1

5．如圖1，已知在△ABC中，AB=AC，∠BAC和∠ACB的平分線相交于點D，∠ADC=130°，則∠CAB的大小是

( )

A.80°B.50°C.40°D.20°

6.若x0是一元二次方程ax2+bx+c=0(a≠0)的2個根，則判別式Δ=b2-4ac與平方式M=(2ax0+b)2的大小關系是

( )

A．Δ>MB.Δ=MC.Δ

二、填空題

7．將一個四邊形的紙片一刀剪去一個角后，所得的多邊形的內角之和是________.

8．觀察下列各組數：(3，4，5)，(5，12，13)，(7，24，25)，(11，60，61)…，發現4=(32-1)÷2,12=(52-1)÷2,24=(72-1)÷2….若設某組數第一個數為k，則這個組的數為(k,________,________).

圖2

圖3

9．如圖2是一個樹形圖的生長過程，依據圖中所示的生長規律，第15行的實心圓點的個數等于________.

10．如果表示正方形ABCD各邊長的代數式如圖3所示，那么陰影部分的面積是________.

11.A,B,C,D,E,F這6個足球隊進行單循環賽，當比賽進行到某一天時，統計出A,B,C,D,E這6個隊已分別比賽了5，4，3，2，1場球，由此可知，還沒有與B隊比賽的球隊是________

12.△ABC內接于⊙O，D是邊BC上的中點，若∠ABC+∠DAC=90°，則△ABC是________三角形.

三、解答題

13．某同學買某種鉛筆，當他買了x支，付了y元(x，y都是整數)時，營業員說：“你要再多買10支，我就總共收你2元錢，這樣相當于每買30支，你可節省2元錢”,求x,y.

15．已知：關于x的方程①x2-(m+2)x+m-2=0有2個符號不同的實數根x1，x2，且x1>|x2|>0；關于x的方程②mx2+(n-2)x+m2-3=0有2個有理數根且兩根之積等于2.求整數n的值.

16.討論一道開放性試題，教師要求同組每個同學至少要和3個同學交換意見．某學習小組共有11位同學，討論完成后有2位同學說自己和4個同學交換了意見．證明:至少還有1位同學也至少和4個同學交換了意見．

參考答案

13.解根據題意得，y的值只能是1或2.

此時m只能取15,30,45,60….經討論后,只有當m=15，x=5時,才符合題意.

(2)當y=2時，

無論m為何整數均不合題意.故x=5,y=1.

圖4

圖5

(2)能取得最大值,如圖5所示.

15.解由方程①及x1·x2<0，x1>|x2|>0,知x1>0,x2<0.由

Δ=(m-2)2+8>0,

得

x1+x2=m+2>0,x1·x2=m-2<0,

從而

-2

由方程②知

即

m2-2m-3=0,

解得

m=3(舍去)，m=-1,

代入方程②得

x2-(n-2)x+2=0.

因為方程的2個根為有理數，所以

Δ=(n-2)2-8=k2,

即

(n-2)2-k2=8,

得

(n-2+k)(n-2-k)=8,

從而

解得

n=5或n=-1.

16.證明因為甲、乙2人相互討論1次，每人都說自己討論了1次，在統計時，就被算作了2次.

在11個人中，若每人剛好只討論了3次，則總次數將是11×3=33次，

由于其中有2個人是討論的4次，因此總次數是33+2=35次．

根據前面的分析可知，對每一次討論都有2個人報數，故總次數應該是2的倍數，故總次數>35．即總次數至少是36次，因此一定至少還有1個人是討論的4次．

(浙江奧數網提供)