回熱器板疊流動特性研究

孫生生 韓躍峰 苑 飛 翟 琛

1 引言

熱聲板疊或回熱器是熱聲系統的核心部件，其內部的交變流動和換熱問題得到了研究者的廣泛關注。但是由于基本的換熱系數和流動阻力系數的缺乏，其發展受到了一定的限制。采用半經驗半理論和歸納實驗數據相結合的方法來研究熱聲板疊或回熱器內的交變流動問題，這種分析研究方法使得研究結論的適用范圍受到嚴格的限制，而且由于實驗次數和實驗條件的限制，所得到的結論的適用范圍很窄，不足以為廣泛的工程應用提供依據。而且對于熱聲熱機回熱器來說，其水力半徑通常只有0.1 mm甚至更小的數量級，因此其內部流動參數用儀器直接測量幾乎是不可能的，而借助于CFD軟件模擬流場的強大能力，則可以很方便解決這些問題。借助于有效的理論分析模型，采用數值模擬的方法，研究回熱器的熱力學、流體力學及聲學特點，是解決這一問題的一個有效方法。本文將借助于CFD軟件的強大流體計算能力模擬其內部流動狀況［1］，其結論既可以驗證試驗結果的可靠性也可以發揮指導試驗設計等重要作用。

回熱器內部氣體流動動量方程可寫成［2］:

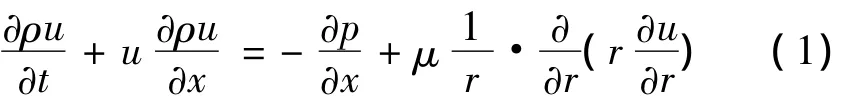
式中左邊前兩項為控制體內部動量變化量，通常稱為慣性項，右邊第一項為壓力梯度項，第二項為粘性項。通常情況下，小型制冷機回熱器中的氣流速度很小，因此，左邊第二項與其它項相比很小，可以忽略不計［3-4］。回熱器交變流動瞬態流動的摩擦阻力系數定義式應為:

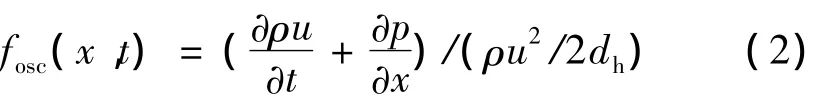
其中:dh是回熱器中板疊間隙的當量直徑;fosc(x，t)為瞬時交變流動摩擦阻力系數。

交變流動與穩定流動的根本區別在于交變流動回熱器中壓力降是由于粘性阻力和慣性力聯合作用的結果，對于穩定流動回熱器中的壓力降，則完全是由于粘性力產生的。慣性項和壓力梯度項、粘性項的相對大小是交變流動與穩定流動存在差別的根本原因。式(1)忽略第二項，經過積分后得出:

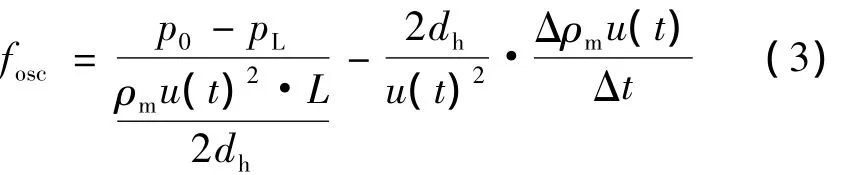
這是回熱器交變流動平均摩擦阻力系數表達式［1］。其中，p0，pL分別為回熱器兩端測得瞬時壓力值;平均密度，Δρ= ρ- ρ為回熱器兩m0L端的密度差;由后面的模擬結果可發現，板疊內的速度分布近似呈線性，因此可以取u(t)=T為波動流過板疊的時間，T為聲波的周期，λ為波長。

式中:p0，pL，ρ0，ρL，u0，uL為任意時刻瞬時值。在Fluent中可以很方便的計算出來，而這也正是CFD模擬最大的優點，即試驗中測量不到的死角處的參數，在CFD軟件中可以很方便的得到。

本文僅進行了無溫度梯度的回熱器流動特性探索性研究，有溫度梯度，以及流動特性與頻率的相互關系等一系列工作都將在今后的研究工作中逐步展開。另外對于數值模擬來說，摩擦阻力系統的時間分布也可得到，因此可以得到在一個周期內整個板疊長度上的平均摩擦阻力系數。

2 初步模型設計

為了使研究的問題更加貼近實際，對回熱器的建模進行了認真的考慮，從頻率選擇、所采用的工質到回熱器板疊間距設計［5-6］都進行了詳實的計算。因為只研究等溫情況下回熱器內流動，此處略去了冷熱端換熱器的設計。

綜合考慮選擇300 K氦氣作為氣體工質，聲速1 030 m/s;氣體平均充氣壓力為2 MPa，驅動壓比定為2%，即驅動壓力幅值為4×104Pa;工作頻率為450 Hz，由此可確定熱聲制冷機半波長諧振管總長Lt=1 144 mm;選用不銹鋼材質的平板型板疊，兼顧建模方便，板疊厚度取為0.5 m，求得板疊中心位置(距離左端入口處)及板疊長度為xc=79.3 mm。

3 物理模型簡化設計

由初步設計結果進行建模。

諧振管長1 144 mm。回熱器板疊長90 mm，中心位置距左端79.3 mm，則板疊左端距諧振管左端34.3 mm，間距 0.38 mm，厚度 0.5 mm。板疊 19 片(合計9.5 mm)，間隔 20 個(合計 7.6 mm)，總厚度應為17.1 mm，中間為板疊。

建模如圖1所示，由于管長與直徑相差過大，只給出回熱器板疊部分，且圖中所示均為上半部分。在靠近中間的板疊縫隙中間及兩端共計設了8個點，監測其壓力及速度。

圖1 回熱器內監測點分布Fig.1 Monitor point distributions in regenerator

4 模擬結果及分析

4.1 回熱器內壓力與速度分布的特點

諧振管中加入回熱器后，壓力及速度分布相比空管時必然要出現變化，而充分了解回熱器板疊內的壓力速度分布情況，對回熱器結構的設計及性能提高有很大幫助。

如圖2，圖3所示為400 Hz工作頻率時回熱器內壓力、速度分布圖。

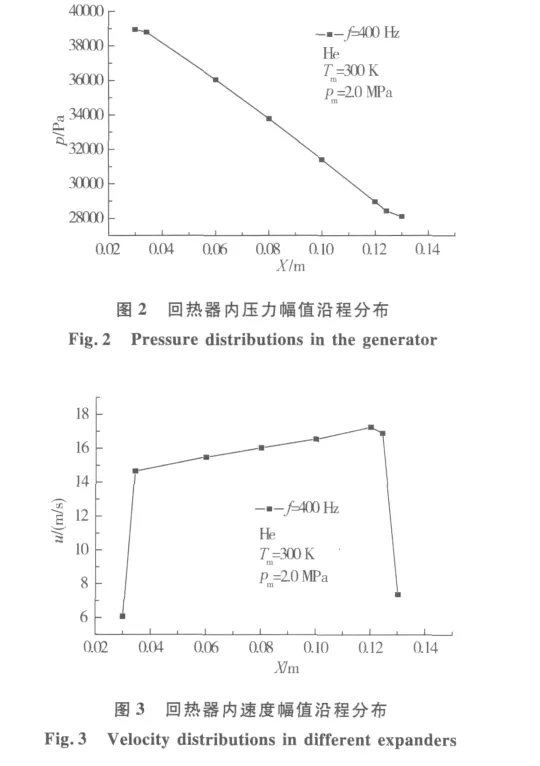
顯然，在回熱器的兩端壓力及速度幅值都出現了突變，回熱器內的壓力及速度不再是正弦或余弦曲線狀分布，而是呈具有一定斜率的近似直線的線性分布(對于這一結果的原因作者尚形不成系統的解析，還有待進一步分析比較)。而速度在回熱器進出口處出現突變是因為流道的突變，在進口處，流道突降，為入口前的Φ(孔隙率)倍，因此流速突增，出口處，流通面積又突增，為出口前的Φ(孔隙率)倍。

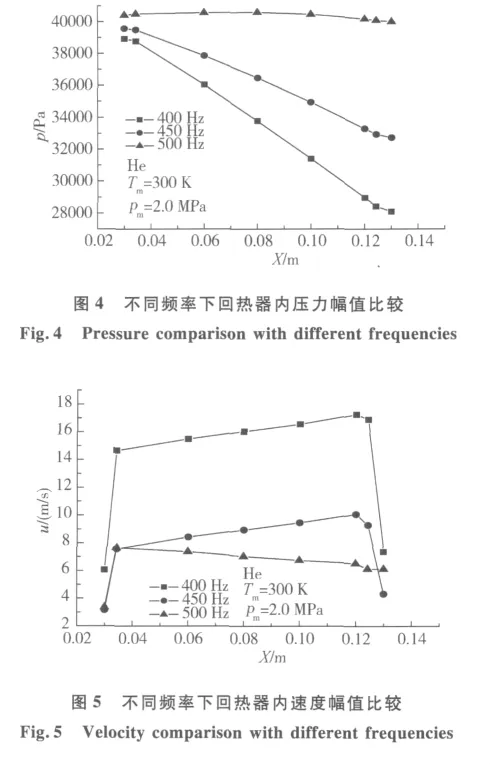
在工質條件、充氣壓力及驅動壓比不變的情況下，改變驅動頻率為450 Hz、500 Hz，再對回熱器內壓力速度分布進行模擬計算。三者壓力、速度分布比較如圖4，圖5所示。回熱器內壓力及速度分布幾乎均呈線性分布，而不再是空管狀態時的正弦或余弦分布。

4.2 高頻回熱器交變流動阻力探討

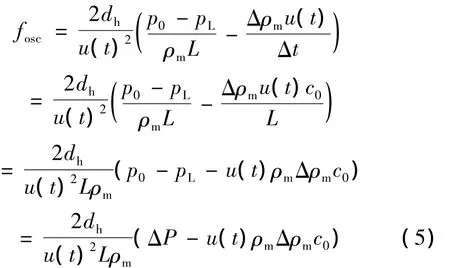
式中:c0為聲速;在工質、充氣壓力、驅動頻率及壓比一定的情況下，dh，Δt，L 是固定的;Δρm數量基在10-2;因此平均密度ρm的影響可以看作不變的，故上式又可寫成:

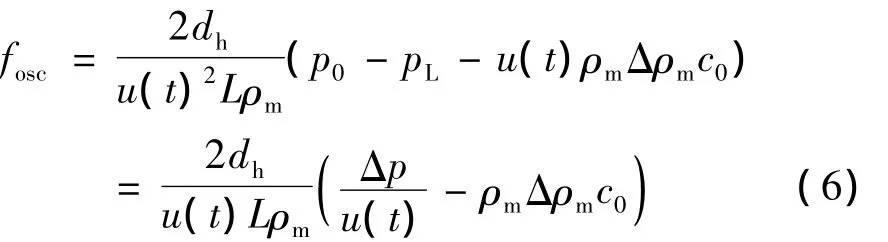
因此在高頻交變流動時，fosc將主要取決于的值。

根據式(6)及模擬計算結果，取模擬結束時的瞬時值計算。

以400 Hz為例，取t=9.000 0×10-2s的各項瞬時值計算，得:fosc1=0.046 3。

這就是工質為300 K的 He氣，充氣壓力2.0 MPa，驅動壓比為1.02，頻率400 Hz，該時刻回熱器的平均流動瞬時摩擦阻力系數。

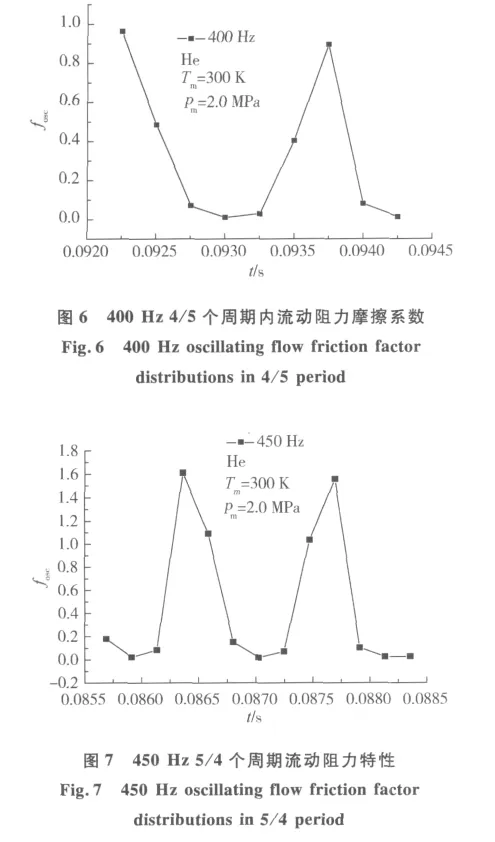
同理可以對450 Hz，500 Hz任意時刻回熱器板疊的瞬時流動阻力系數進行計算。例如圖6，圖7所示，分別為400 Hz驅動頻率時4/5個周期、450 Hz一個多周期時回熱器的流動阻力系數分布圖，由此可以推斷其變化將是波動性的，即回熱器的交變流動阻力系數也隨時間變化呈現出波動性，這也是今后將要研究的問題。

5 結論

利用Fluent對熱聲回熱器內的聲場分布進行了初步的、探索性的分析研究。在此處，Fluent充分顯示了其應用于該領域的優勢，即不受線性假設的限制，其計算結果清晰地顯示了回熱器入口處壓力速度的不連續性，克服了DeltaE等的局限性。

分析研究表明熱聲回熱器內部的聲場分布與寬流道的諧振管內的聲場分布不同。在熱聲回熱器內部壓力和質點速度分布不再為駐波形態，而是沿板疊長度近似呈線性分布;回熱器內部的摩擦阻力系數是時間和位置的函數，對一個一個周期內回熱器的流動阻力系數進行分析，發現其變化具有波動性，即回熱器的交變流動阻力系數也隨時間變化呈現出波動性;回熱器的進出口表現出明顯的入口效應。

對熱聲回熱器在無溫度梯度下流動特性的研究表明，交變流動表現出與穩定流動完全不同的特點，在對交變流動進行研究時經典熱力學、傳熱學、流體力學的理論應謹慎采用。

1 孫生生，張富珍，宋福元.基于Fluent的熱聲異形諧振管壓比研究［J］.低溫工程.2008(1):14-16.

2 王希龍.脈沖管制冷機和回熱器內交變流動特性實驗研究［D］.北京:中國科學院理化技術研究所，2005.34-36.

3 何雅玲，吳沛宜.網狀填料交變流動壓降和阻力的實驗研究［J］.低溫與超導，1990，18(1):14-22.

4 候宇葵.高頻微型脈沖管制冷機設計方法及調相機理研究［D］.北京:中國科學院力學研究所，2002.

5 Richardson E G，Tyler E.The transverse velocity gradient near the mouths of pipes in which an alternating or continuous flow of air is established［J］.Pro.Phys.Soc.Lond.，1929，42:1-15.

6 Tu Qiu，Li Qing，Guo Fangzhong，et al.Temperature difference Generated in thermo-driven thermoacoustic refrigerator［J］.Cryogenics，2003，43(9):515-522.