平衡常數與正逆反應速率常數之間關系的探討

李學慧 吳正舜伍強賢 陳義峰 劉雪蓮

(華中師范大學化學學院 湖北武漢430079)

平衡常數與正逆反應速率常數之間關系的探討

李學慧 吳正舜*伍強賢 陳義峰 劉雪蓮

(華中師范大學化學學院 湖北武漢430079)

從動力學與熱力學的一致性原理出發，在知道可逆化學反應機理與不知道可逆化學反應機理的兩種情況下，探討了平衡常數與正逆反應速率常數之間的關系，確定了可逆反應平衡常數在不同情況下與正逆反應速率常數之間的關系式。

對于可逆反應，如果不知道反應機理，是否可以根據熱力學條件，由正反應動力學方程建立逆反應動力學方程呢?初看起來似乎是可能的，因在反應達到平衡時，由正反應動力學方程r1=kf1(ci)和逆反應動力學方程r－1=k－1f－1(ci)，可以得到:

其中K是平衡常數，f1(ci)，f－1(ci)是反應物與產物的濃度函數。從式(1)可知:若已知k1和K就可得到k－1，同時，若已知f1(ci)和K，也就可以得到f－1(ci)，即已知正反應動力學方程可得到逆反應動力學方程。但實際問題并不那么簡單，因為對于一個可逆反應，其化學反應的計量方程式的寫法不同，可以有幾個不同的K值，到底哪一個K值代入(1)式才能得到正確的結果，這就是所謂的動力學與熱力學的平衡一致性問題。

其反應速率方程為:

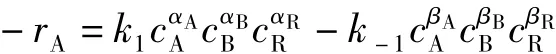
當反應處于平衡時，有－rA=0，則由上述速率方程得:

而當反應達平衡時，由熱力學平衡可知平衡常數滿足下式:

式中因A，B為反應物，其計量系數vA，vB取負值。

設v為正數，由式(3)有:

(2)～(4)式均是說明化學反應達到平衡這一事實，要滿足其一致性，則有下式成立:

因此必有等式:

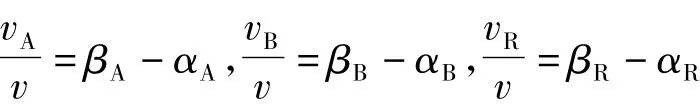
式(6)中的v為化學計量數［1］，即化學反應機理中速率控制步驟中出現的次數，也就是以給定的化學計量系數反應為基礎，保證最終產物中不出現反應的中間活化產物時，某一步必須進行的次數，這可從下面的示例中加以說明。

假設氫氣與氮氣在鐵上進行催化反應經歷如下步驟:

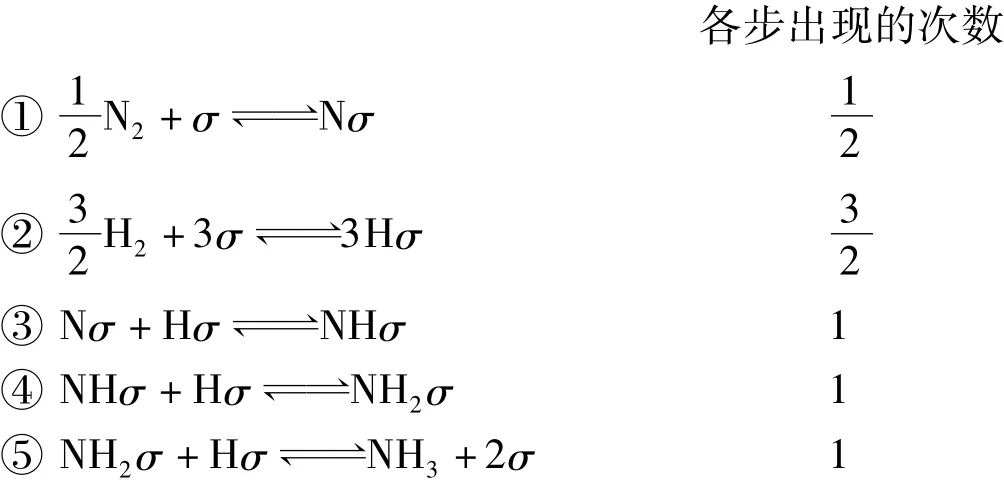
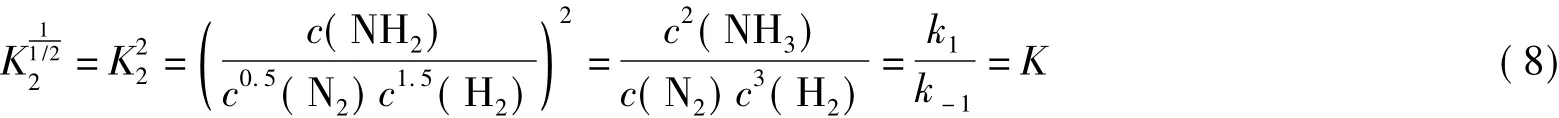
由于正逆反應速率常數不因化學反應的化學計量系數改變而改變，式(7)與式(8)一致正好說明了這一點，此時也滿足了動力學與熱力學的一致性。

再如，假設SO2在鉑上進行催化反應經歷如下步驟:

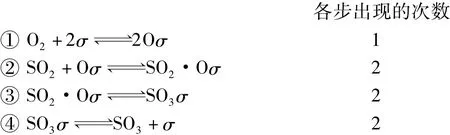
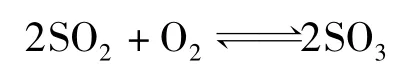
的化學計量數為2，此時有:

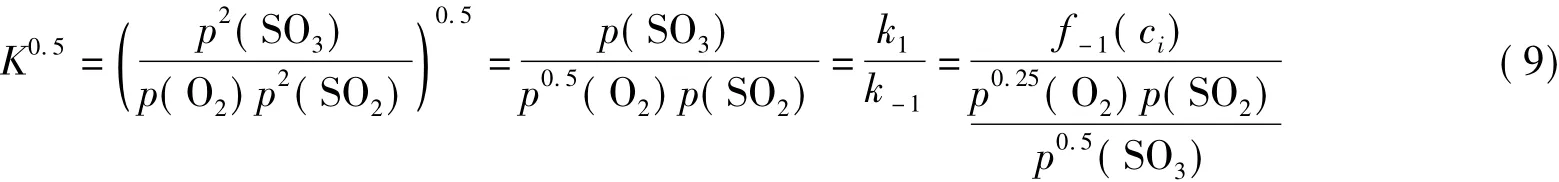
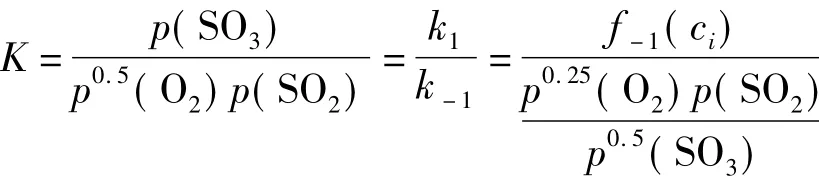
然而，對于不知道其可逆反應機理時，平衡常數與正逆反應速率常數間的關系如何呢?這里只有當化學反應的計量系數與其正逆反應的動力學級數一致或由正、逆反應動力學方程中的濃度項組合后達到一致時，才有平衡常數與正逆反應速率常數間滿足式(1)，這可從式(10)得知，否則，它們之間的關系不能滿足式(1)，而要根據化學計量數v確定其關系。

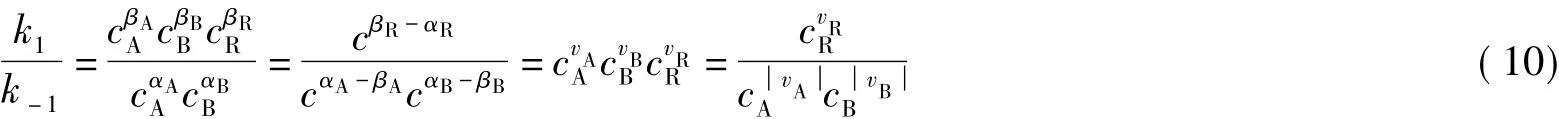
上面的示例說明，要滿足動力學與熱力學的一致性，當不知道反應機理時，只有當化學反應的計量系數與動力學反應級數一致或由正、逆反應動力學方程中的濃度項經組合后達到一致時，平衡常數與正逆反應速率常數之間才滿足式(1);當知道反應機理時，只有當化學計量數為1時，平衡常數與正逆反應速率常數之間才滿足式(1)。否則，要根據化學計量數v，才能確定平衡常數與正逆反應速率常數之間的關系，即它們之間的關系滿足式(6)。

［1］ 李紹芬.反應工程.第2版.北京:化學工業出版社，2000

［2］ 陳甘棠.化學反應工程.北京:化學工業出版社，1990

［3］ Levenspiel O.Chemical Reaction Engineering.3rd ed.New York:John Wiley＆Sons，1999

* 通訊聯系人，E-mail:wuzs@mail:ccnu.edu.cn