三維陷落腔脈動壓力分布特性實驗研究

戴紹仕，姚熊亮，李 卓

（哈爾濱工程大學船舶工程學院，哈爾濱 150001）

三維陷落腔脈動壓力分布特性實驗研究

戴紹仕，姚熊亮，李 卓

（哈爾濱工程大學船舶工程學院，哈爾濱 150001）

文章針對均勻流場中三維深型陷落腔因流分離而產生的流激振蕩問題開展了一系列的實驗研究。在來流流速為0攻角時實驗時的雷諾數變化范圍：Re=1.55×105～8.74×105。實驗中分別測量了三維深型陷落腔側壁周向及垂向流體壓力，分析了腔體內脈動壓力周向、垂向的分布規律及腔口處剪切層自持振蕩特性。實驗結果表明：均勻流場中三維深型陷落腔內脈動壓力分布較為復雜。在剪切層隨邊處的脈動壓力最大，隨邊角點處脈動壓力隨相對高度的增加而陡降為0，但腔口導邊及側面處的脈動壓力隨相對高度增加而略有增大。剪切層自持振蕩頻率的無量綱數St數隨Re變化為一常數值，但其值比氣流場中二維陷落腔的St數略大。

深型陷落腔；均勻流；流激振蕩；脈動壓力；實驗研究

1 引 言

陷落腔結構被廣泛地應用在航天航空領域、航海領域、水利工程等領域中，如飛機起落架輪蓄井、船用海底閥箱及相關儲液系統、槽形壁面的風洞和水洞等都屬陷落腔結構。人們通常認為在三維陷落腔內的水是“死水”，即“死水”暗示著腔內流體的流速為0。但實際上當水流流過陷落腔時在腔口的導邊處會發生流分離，然后因逆壓的存在而產生渦體運動和剪切層自持振蕩的現象。在剪切層振蕩過程中將陷落腔內部水體與外部水體分開，使得腔內形成一循環水系，在此循環水系內有一大渦做低周運動，此時在腔體內部存在一種復雜的、垂向的、不穩定的三維流體運動。腔內較強脈動壓力的變化可能誘發結構產生疲勞損傷或破壞。

到目前為止，有關二維陷落腔流激振蕩問題的研究已取得了較為豐碩的成果[1-7]，但多數研究主要集中在氣流場作用下二維陷落腔剪切層自持振蕩頻率特性的驗證與對比上，不僅忽略了腔內流體運動的三維效應而且不涉及腔體內部流體脈動壓力的分布特性，而剪切層自持振蕩作用會使陷落腔內部產生一種復雜的、垂向的三維流體運動。在這種情況下陷落腔內部的水動力問題還鮮有論文發表。

有鑒于此，本文在均勻流場中不同來流流速的情況下開展了三維深型陷落腔流激振蕩問題的系列實驗研究，給出了三維深型陷落腔內部脈動壓力周向和垂向分布規律，以及剪切層的振蕩特性，揭示了深型陷落腔內部流體運動機理，為三維深型陷落腔的疲勞計算提供參考依據。

2 實驗模型與測量設備

實驗在哈爾濱工程大學拖曳水池開展，拖曳水池長108m、寬7m和深3.5m，水池拖車最大速度可達6m/s，實驗時水溫為20°。實驗載體—船模全長3.8m，寬1.0m和高0.8m，吃水0.4m、干弦0.3m，深型陷落腔的長×寬×高為 0.225×0.3×0.3，高跨比 H/L=1.333，見圖 1，實驗流速范圍 0.6～3.39m/s，Δv=0.31m/s。在實驗模型安裝時為避免實驗載體在實驗中發生橫搖、縱搖及不必要的振動而影響實驗測試結果，本文在實驗時將實驗載體用80#槽鋼與拖車前梁鋼性連接，并在前梁與槽鋼的連接處、槽鋼與實驗載體的連接處分別墊上厚為10mm的橡膠墊，見圖2。為防止實驗過程中腔體內存有空氣，在三維陷落腔頂面中心設置φ30的排氣管。

實驗采用法國產的EPX-N12-0.7B/LTM/Z*微型壓力傳感器，采用LDS Nicollet多通道數據采集系統同時配有DH3842可編程應變放大器1臺和電荷放大器1臺，采樣頻率為0.5kHz，實驗所測的穩定段時間不小于15s。

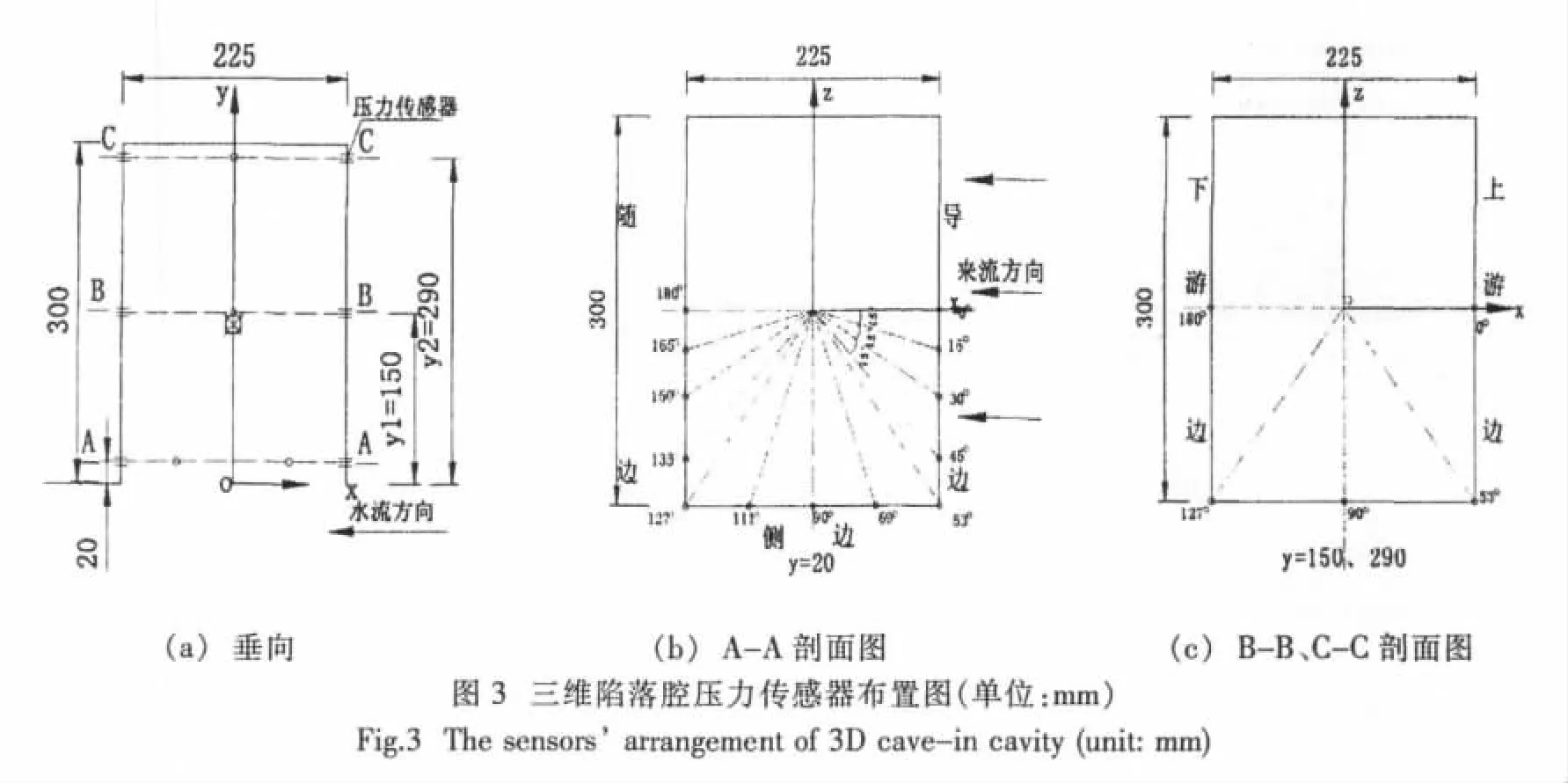
實驗測量設備（壓力傳感器）分別布置在深型陷落腔腔口、垂向中截面及頂截面側壁處，因深型陷落腔流體運動的對稱性沿腔體周向僅布置一半壓力傳感器，為詳細地觀測腔口處剪切層振蕩特性在腔口處布置了較多的壓力傳感器，傳感器布置圖如圖3所示。

3 數據分析參數

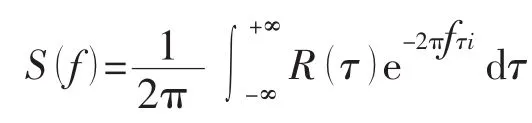
式中：ν為運動粘滯性系數，m2/s；V∞為流向速度，m/s；L為特征長度，本文取腔口在流向上的長度，m；fm為流體剪切層處自持振蕩的各階頻率，Hz；ρ為實驗狀態下流體密度，kg/m3；p′（θ,t）為流體脈動壓力均方根值，Pa。

4 實驗結果分析

本文實驗流速范圍在0.6～3.39m/s，間隔為0.31m/s，共計10種流速。由腔體內三層側壁脈動壓力分布結果可以明顯地看出在深型陷落腔體內存在復雜的流體運動，為詳細地揭示腔內流激振蕩特性，本文分別從脈動壓力分布規律和腔口剪切層振蕩特性進行分析，文中相對高度yi/H及各邊名稱的定義如圖 3（a）～（c）所示。

4.1 脈動壓力系數分布特性

4.1.1 脈動壓力系數周向分布特性

深型陷落腔流體脈動壓力系數的周向分布規律見圖4，圖5給出了高雷諾數時脈動壓力系數的周向分布規律。

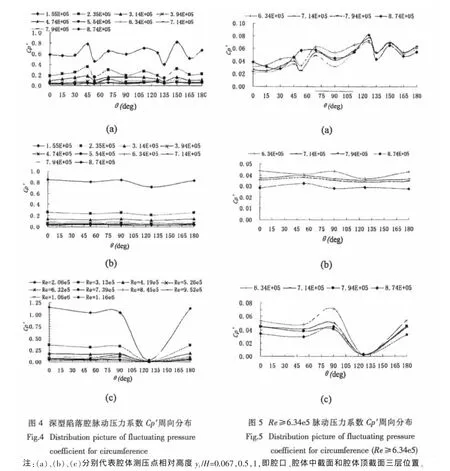
由圖4（a）～（c）從整體上看Cp′在深型陷落腔內周向分布規律并不一致，但Cp′都隨Re數的增加而減小。腔口處的脈動壓力系數分布規律見圖4（a）和圖5（a），當來流流速很小時Cp′波動較大，隨來流流速的增加Cp′的周向分布達到穩定（如（a）），當腔口處Cp′達到穩定時Cp′隨θ的增加而略有增大，在腔口隨邊處（θ=127°～180°）的 Cp′比導邊（θ=0°～53°）處的 Cp′大，且在隨邊角點（θ=127°）處 Cp′最大。呈現出隨邊的脈動力＞側面的脈動力＞導邊處的脈動力，這正證明了在陷落腔腔口處存在剪切層振蕩現象，且越向下游隨邊處剪切層振蕩越為強烈，所以腔口隨邊處存在著最大的Cp′。

由圖4（b）和圖5（b）與腔口處的脈動壓力相比，深型陷落腔中截面處脈動壓力的周向分布較為均勻，Cp′曲線趨于平坦（見圖（b-2）及（a-2））。在相同雷諾數時腔中截面側壁的Cp′遠小于腔口隨邊處Cp′，但其值要略大于腔口導邊處的Cp′。

由圖4（c）和圖5（c）可見無論是低雷諾數還是高雷諾數，深型陷落腔頂截面處的Cp′在θ=127°（即頂截面下游方向角點處）時陡降為0，而在其它側點處Cp′值較接近。在實驗數據分析中發現在θ=127°時穩態壓力系數Cp=0，由此也可說明Cp′陡降為0的原因是在深型陷落腔腔頂截面下游角點處水流沒有流動，所以脈動壓力系數陡降為0。

4.1.2 脈動壓力系數垂向分布特性

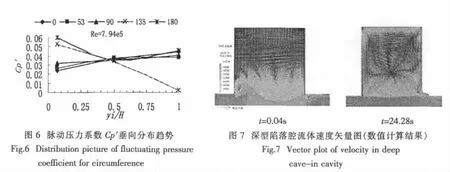
學者們更為關心的是脈動壓力系數Cp′沿腔體深度方向的變化情況。由上述分析可知高雷諾數時深型陷落腔內Cp′分布趨于穩定，且不同雷諾數時脈動壓力系數的垂向變化規律一致，因此圖6以Re=7.94×105為例給出Cp′的垂向分布趨勢。

由圖6清晰可見在yi/H=0.067時θ=135°和180°（即腔口隨邊位置）處的Cp′脈動力最大。隨邊角點（θ=135°）處Cp′隨相對高度的增加而減小，在頂截面處為0，而其它側點處的脈動壓力隨相對高度的增加而略有增大，呈現出腔體頂截面處Cp′＞中截面處Cp′＞腔口導邊及側邊處的Cp′。即深腔內部也存在著較大的脈動力。腔口隨邊處脈動力最大是因為隨邊正對于來流方向，其一是在腔口處剪切層振蕩十分明顯，其二是隨邊壁面會給予來流流體一反向阻力，所以腔口處隨邊脈動力較大；而頂截面處的流體受腔內循環水流運動的影響，逆時針運動的水流同樣會因壁面給予的反向阻力而產生較大的脈動力（除下游面角點外）。為清晰地理解腔內的流動運動狀態圖7給出了深型陷落腔內流體運動初始時及穩定時的矢量圖，以增加腔內流體運動的感性認識，鑒于數值計算的文章已發表[8]，本文不再對數值計算方法及結果進行詳細討論。

4.2 深型陷落腔剪切層自持振蕩特性

實驗中存在各種干擾信號所以本文采用Matlab先濾掉各種干擾信號后，再對腔口處剪切層自持振蕩的頻率進行分析。圖8給出了不同速度時深型陷落腔剪切層處脈動壓力的自功率圖。

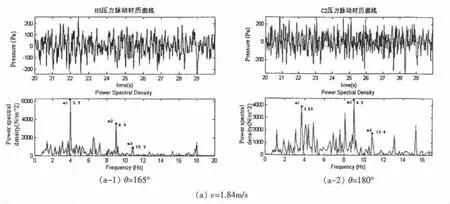
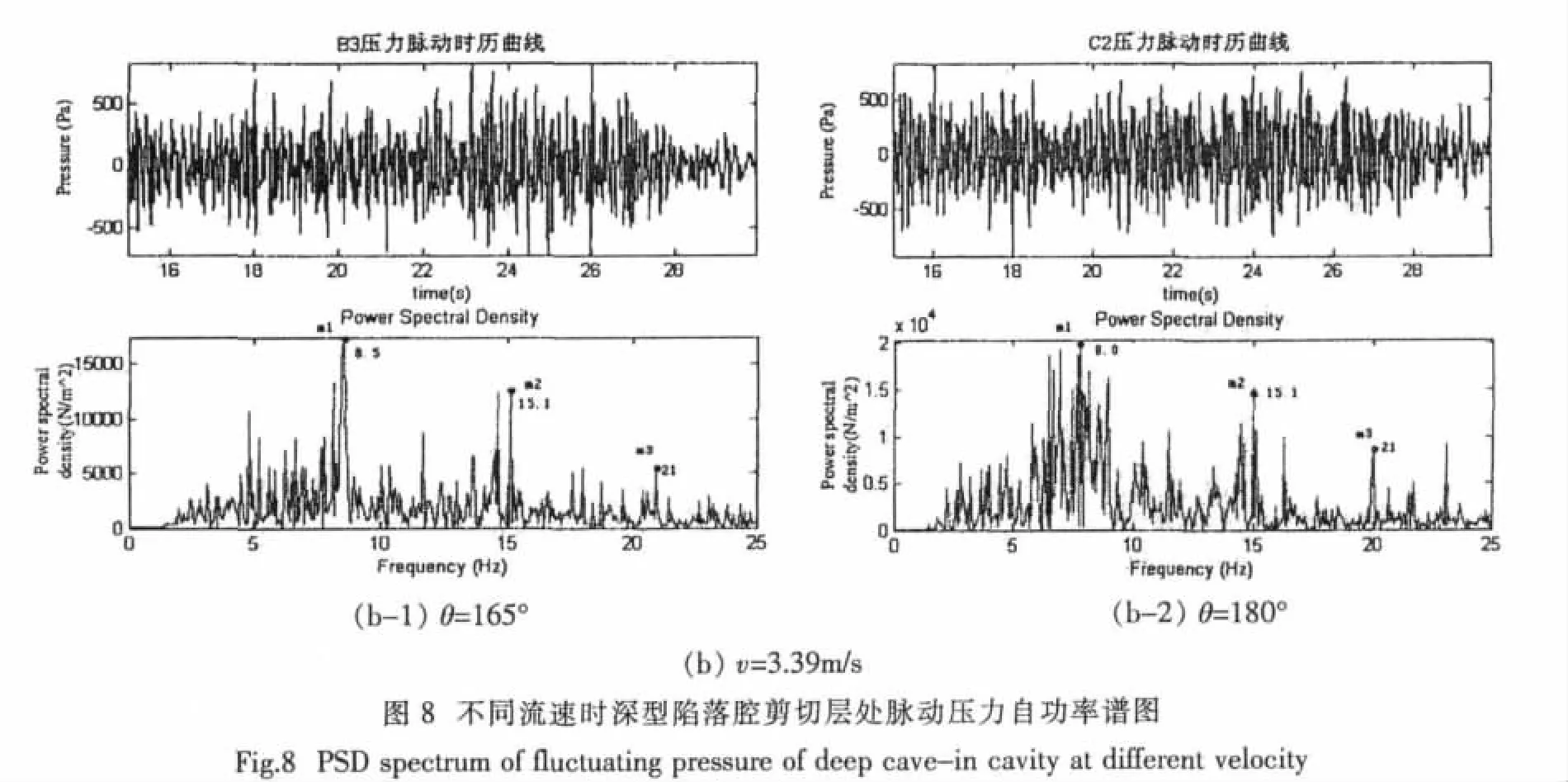
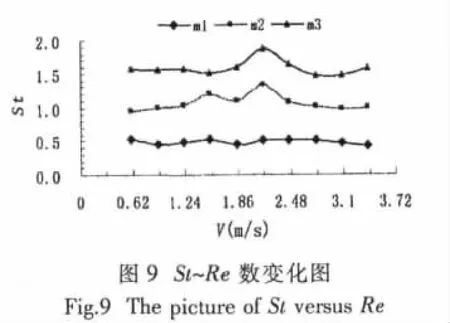
由圖8（a）和（b）可見在相同來流流速時腔口剪切層隨邊處的振蕩頻率是基本一致的，隨來流流速的增加剪切層隨邊處的振蕩頻率增大，脈動力明顯地增強，這證實了脈動壓力隨Re數的增加而增強，Cp′隨Re數的增加而減小。由公式（2）折算出各階頻率對應的St數隨Re的變化為同一常數值。本文并根據實驗數據采用最小二乘法對St～Re的曲線進行擬合，擬合公式見公式（4）。圖9中給出了St數隨Re的變化規律。

由圖9可見相同階的St數隨Re數變化為同一常數，即

m1≈0.5，m2≈1.1，m3≈1.7。本文折算的St數比Rossiter[6]在低Ma數時研究的二維陷落腔剪切層振蕩的 St數略大（m1≈0.42，m2≈1，m2≈1.57），與何祚鏞[2]測得結果較為接近（m1≈0.55）。 但深型陷落腔的St數隨Re數的變化規律與二維陷落腔的變化規律一致[2-6]。同時本文根據實驗數據給出了深型陷落腔在均勻流場作用下St數的估算公式：

5 結 論

本文采用一系列的物理實驗研究了深型陷落腔在均勻流場作用下脈動壓力分布特性及剪切層振蕩特性，主要得出以下結論：

（1）三維深型陷落腔內Cp′的周向分布都隨Re數的增加而減小，但脈動壓力隨Re數的增加而增加。

（2）三維深型陷落腔腔口隨邊處的Cp′最大，且Cp′隨相對高度的增加而減小，隨邊角點處的Cp′在yi/H=1時陡降為0；腔口導邊及側面的Cp′隨相對高度的增加而略有增大，即深型陷落腔在頂截面處也存在著較大的脈動力。

（3）均勻流作用下三維深型陷落腔剪切層自持振蕩各階頻率對應的St數隨Re數的變化為一常數，此常數比氣流場作用下的二維陷落腔的值略大。文中給出均勻流中三維深型陷落腔St數的估算公式。

[1]D’yachenko A Yu,Terekhov V I,Yarygina N I.Vortex formation and heat transfer in turbulent flow past a transverse cavity with inclined frontal and tear walls[J].International Journal of Heat and Mass Transfer,2008,51:3275-3286.

[2]何祚鏞.結構振動與聲輻射[M].哈爾濱:哈爾濱工程大學出版社,2001:147-182.

[3]康 莊.月池流噪聲及水動力特性的實驗研究[D].哈爾濱:哈爾濱工程大學,2006:4-100.

[4]朱習劍,衣云峰,何祚鏞.突出腔的流激振蕩激勵源[J].哈爾濱船舶工程學院學報,1994,15(1):26-36.

[5]Jacquin,Geffroy.Large-eddy simulation of a subsonic cavity flow including asymmetric three-dimensional effects[J].Journal of Fluid Mechanics,2007,577:105-126.

[6]Rossiter J E.Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speed[R].R.A.E.Tech.Report 64037,1964:210-235.

[7]Rowley C W,Wlliams D R.Dynamics and control of high-Reynolds number flow over open cavity[J].Annu.Rev.Fluid Mech,2006(8):251-276.

[8]姚熊亮,楊國晶,戴紹仕等.陷落腔剪切層自持振蕩的數值計算分析[J].水動力學研究與進展,2009,24(3):332-340.

Experimental research on fluctuating pressure distribution of 3D cave-in cavity

DAI Shao-shi,YAO Xiong-liang,LI Zhuo

(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

Aiming at fluid induced oscillation problem of 3D cave-in cavity owing to separation flow in uniform,a series of physical experiments was carried out.The range of Reynolds number is Re=1.55e5～8.74e5at zero attack angle of incoming.Circumferential and vertical fluid fluctuating pressures along the deep cavein cavity were measured,meanwhile,distribution of fluctuating pressure and oscillation characteristic of shear layer were analyzed.The results of experiment show that the distribution of fluctuating pressure in uniform field is complex.The fluctuating pressure at the leading edge of shear layer is the largest and fluctuating pressure at angular point drops to zero with the relative height increasing.But the fluctuating pressures at the leading edge and side increase a little with the increment of relative height.Moreover the change of St number of shear layer versus Re number is constant,but the value of St number is larger than the value of two dimensions in the air.

deep cave-in cavity;uniform flow;fluid induced oscillation;fluctuating pressure;experimental research

035

A

1007-7294（2010）05-0451-07

2009-11-17

哈爾濱工程大學國防科技工業技術基礎科研項目（B1920070100）

戴紹仕（1976-），女，哈爾濱工程大學博士生，E-mail:daishaoshi@163.com。

book=457,ebook=44