載波相位確定模糊度及其誤差校正方法①

郭思遠,林 翔

(北京5128信箱,北京100094)

0 引 言

載波相位平滑偽距測量方法廣泛用于GPS或GNSS接收器。在單頻接收機中,為了避免電離層折射效應影響測量精度,平滑時間一般限定為1～2 min的時間。如果應用兩個或多個的頻率,偽距測量值就可以通過含有電離層折射因素的載波相位測量線性組合平滑。在偽距觀測值誤差很小的情況下,經過平滑后的偽距觀測值可用于測定整周模糊度。如果有三個或以上的不同頻率的載波用于測量,就可以組成兩組不同的載波相位測量,模糊度可以通過兩組濾波方程的差分得到。但是,利用這種方法雖然可以提高確定模糊度的準確性,但是也加大了系統的噪聲影響。如果兩個頻率相近,則消除電離層效應的方程式組合將擴大噪聲影響。所以,就要用另外一組折射校正載波相位測量與原有的測量差分,以抵消噪聲誤差。

1 假設條件

假設兩個前提條件:

1)站點與站點之間的測量是完全相同的(從理論上說,這個過程可以用在單一現場測量)。如果一個已知站點坐標,就可以確定任何碼和載波偏差,并且能夠將它們作為接收點對于衛星坐標的角度函數,這樣就可以進行單點測量。經過校準后,方程式就可以在多點測量或者單點測量中應用。

2)假設衛星與衛星之間的測量完全一致。衛星接收器前端過濾器會產生由于不同頻率而造成的鐘差。這會造成寬巷載波測量和與之相匹配碼測量之間的誤差。如果這種偏差很大,就會導致模糊度確定誤差。我們可以通過衛星間的單差解決這個問題。

由于對流層對不同頻率的影響是相同的,在測量過程中電離層折射影響是比較明顯的。在模糊度計算和折射校正線性組合中,對流層因素影響不變。這樣無幾何模型的優勢就在于對流層因素并不會對計算過程造成太大影響。

2 寬巷組合模糊度計算[3]

首先進行兩組低噪聲、折射影響較小、確定模糊度的載波相位測量,以構建兩組寬巷載波相位確定模糊度。為了避免相同公式中用許多不同的頻率符號,以fa,fb和fc表示。

這兩組方程式中,ρ是實際距離(包含對流層折射),I表示為不同頻率引起的電離層影響。同樣,在載波測量中,可以列式

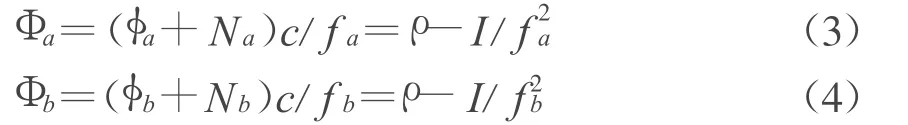
Φa和 Φb為相位值,φa和φb為測量值,N表示載波的起始整周模糊度,c表示光速,在式(1)和式(2)中采用加權平均方法,就能夠消去方程式中多路徑影響,并有效地表示電離層影響。

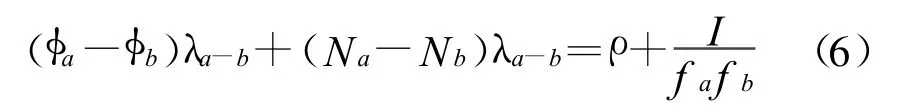
λa-b表示頻率差值的波長。由式(5)、(6)可以得出以下方程

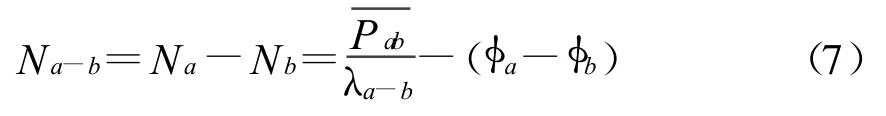
從式(7)中可以看出,只要信號接收器的相位鎖定保持穩定,那么寬巷模糊度就不會改變 。那么,這個值就可以采用加權方法獲得更準確的值。

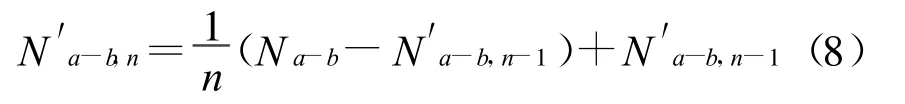
加權后的值可以帶進式(6)中進行寬巷載波相位測量

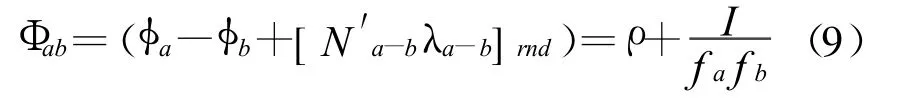
式(8)中為了保證準確的寬巷模糊度,就要保證式N的數量。表1給出了兩種不同系統的相關頻率的波長。GPS的 L1頻率和 L5頻率表示為fa和fc,中間頻率 fb則由兩種頻率表示,GPS L2,伽利略E6均比L2頻率高51.15MHz。

表1 GPS與Galileo系統波長比較

3 寬巷載波相位測量折射校正

上一節中式(9)表示寬巷測量中由電離層影響引起的誤差。這個誤差需要校正。首先從三個相位測量中建立第二個模糊度確定寬巷載波測量方程。因為三個不同頻率能組合兩組不相關的寬巷頻率,那么也就能組成兩組有最大頻率寬度的寬巷組合,就可以用最短時間計算模糊度。

假設 fa＞fb＞fc,寬巷組合由 fb-fc表示,在式(9)中只需要將下標改成b、c,確定了 Na-b和Nb-c的值,Na-c就可以相加得到。所以,第三個載波測量值也就可以得到了。

這兩個方程式中電離層因素是不同的,所以利用線性組合消去電離層因素影響。將式(10)乘以fc/fa并減去式(9),得

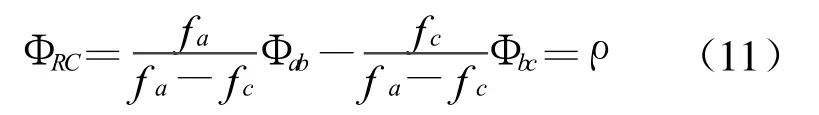
這個方程是沒有電離層因素影響的,已進行折射校正模糊度確定的方程式。

4 消除噪聲誤差[5]

減少折射誤差的過程引起了噪聲誤差在方程式的擴大。在三個寬巷頻率之中,各自之間的噪聲誤差是不相關的。假設,在各個載波相位測量中都可以確定模糊度(將它們表示為 Φa,Φb,Φc),可以得到方程式:

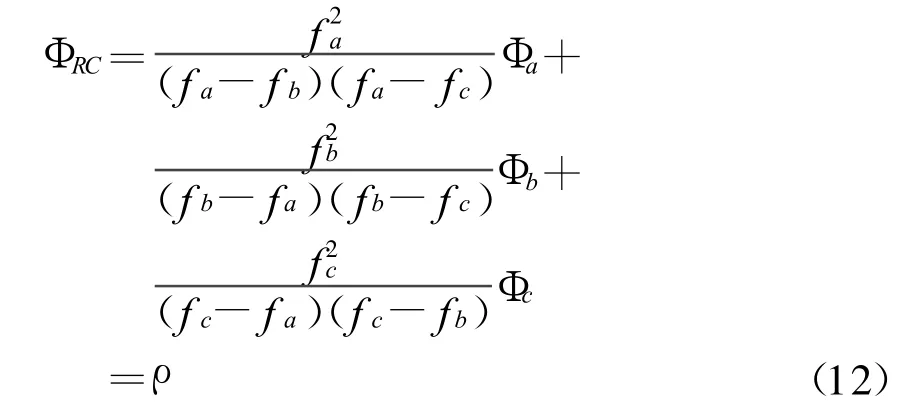
以L1和L5為例,與GPS和Galileo相似。表示為FA和FB頻率,可以看到噪聲誤差是作為中間頻率FB的一個函數。假設相位測量中確定波長時,在各個測量中有相當于1 cm的噪聲誤差;假設各個測量中噪聲誤差是相同的。那么就能用波長表示噪聲誤差,如1.0、fc/fa,1.34 cm三種方式。雖然這個誤差很小,但是包括了多路徑誤差效應。測量中預想的噪聲誤差是方程式(12)中的三個系數的平方和的平方根的值。表2給出了兩種不同中間頻率所產生的噪聲誤差,當每個相位噪聲都是1 cm,從表2可以看出,Galileo E6頻率的噪聲誤差比GPS L2頻率噪聲要小的多。

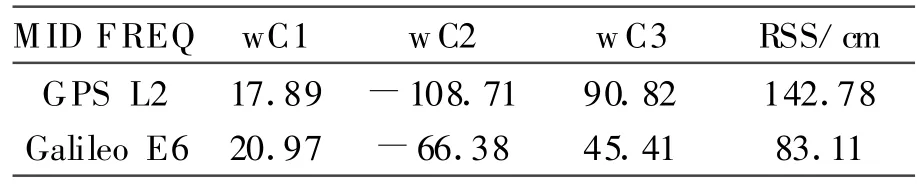
表2 GPS L2與Galileo E6中間頻率噪聲誤差比較

5 載波平滑載波

既然載波相位可以平滑偽距測量,那么可以利用另外一組低噪聲,已知整周模糊度的載波平滑式(10)生成的載波測量,來減小噪聲誤差。

假設每個相位測量噪聲誤差為1 cm,那么,低噪聲,折射校正方程式可以歸結為三個因素。上述方程式中的a,b,c必須滿足以下三個條件:

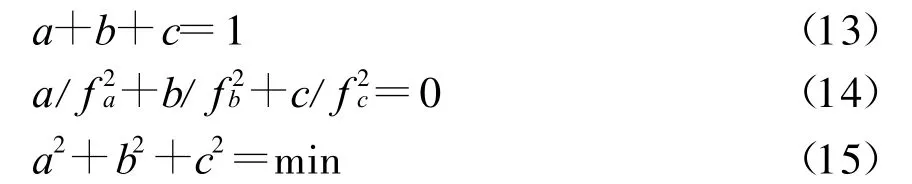
第一個方程保證測量范圍不被壓縮,第二個方程保證消除了電離層誤差。第三個方程則是放大低噪聲。由式(13)式可得

將c代入式(14),則

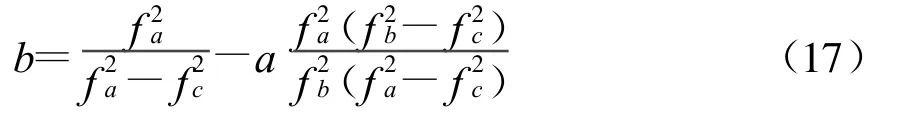
將式(17)簡化為

將式(16)、(18)式代入式(15),可得出最小值v

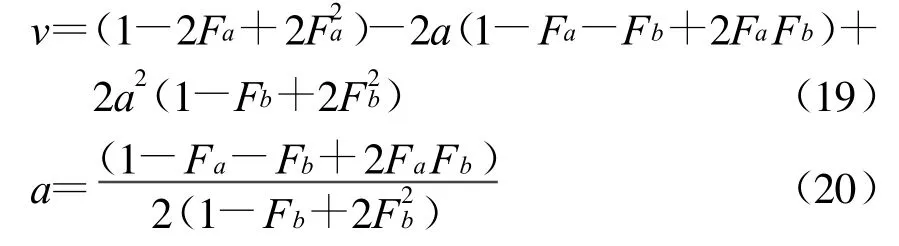
將b和c的值帶回式(18)、(16),如果中間頻率為上述頻率時,表3列出了a,b,c的值和噪聲影響。從表3可以看出,當模糊度確定時,GPS L2頻率的噪聲誤差比Galileo E6要小。

表3 模糊度確定時GPS與Galileo系統噪聲誤差

ΦM假設為最小噪聲誤差,那么可以列式:

式(11)結果和式(21)結果都含有折射校正誤差。將兩式相減,得到的結果是三頻噪聲誤差和(21)式中的模糊度初始誤差。用O表示為

通過加權方法計算O,那么它的值將會近似于式(21)的誤差。

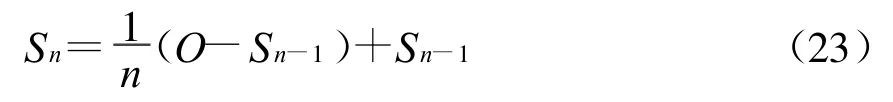
然后再將得出的值帶進式(21),得

6 結 論

載波相位平滑偽距測量在偽距觀測值誤差很小的情況下,經過平滑后的偽距觀測值可用于測定整周模糊度。在三個或者以上不同頻率的載波測量時,可以利用兩組不同載波相位測量,模糊度就可以通過兩組濾波方程的差分得到。運用這種方法的同時也加大了系統的噪聲影響(如果兩個頻率相近,則消除電離層效應的方程式組合將擴大噪聲影響)。利用了另外一組折射校正載波相位測量與原有的測量進行差分以抵消噪聲誤差。

[1] 常 青 ,柳重堪,張其善.GPS載波相位組合觀測值理論研究1[M].航空學報 ,1998,19(5):12-161

[2] 魏子卿,葛茂榮.GPS相對定位數學模型[M].北京:測繪出版社,1997.

[3] 楊 劍.利用GPS三頻組合觀測值求解模糊度理論及算法研究1[M].武漢:武漢大學,2004.

[4] 伍岳.第二代導航衛星系統多頻數據處理理論及應用[D].武漢:武漢大學,2005,71-76.

[5] Navcom Tech Inc.Method for using three GPS frequencies to resolve carrier-phase integer ambiguities US:1864078[P].Nov 15,2006.