紅線寬度變化時緩和曲線邊線展寬方法

田海勇，耿新田

(洛陽規(guī)劃建筑設計有限公司，河南洛陽 471000)

紅線寬度變化時緩和曲線邊線展寬方法

田海勇?，耿新田

(洛陽規(guī)劃建筑設計有限公司，河南洛陽 471000)

兩條不等寬的道路相對接時，如果中線是緩和曲線，特別是在內邊線加寬的情況下，邊線平滑連接涉及復雜的曲線解算。本文就此問題闡述解決的思路和方法。

緩和曲線；邊線要素；變寬；邊線對接

1 引 言

城市道路經常有不等寬的兩條道路相對接的情況[1]，對于中線是直線、圓曲線的情況，其邊線要素很容易計算，但對于中線是緩和曲線的兩條不等寬道路的對接，特別是考慮到交通流量，有的內邊線還要加寬，這對邊線要素的正確解算提出了新的要求。通常情況下，為了簡化計算，一般采用近似方法按圓曲線處理，由于不能保證相切關系，沿曲線轉彎過程中會產生多處折點，道路寬度變化也不均勻。

為了保證相切關系，使邊線連接處平滑過渡，體現道路設計的思路，嚴格控制各項要素指標，邊線過渡段可采用緩和曲線進行連接。本文就這一方法進行詳細論述。

2 數學模型

如圖1所示，ZH處的半路寬為D1，HZ處的半路寬為D2，從ZH到HY、HZ到YH，內邊線加寬值為△D，其內邊線加寬終點分別是A和B，我們可以將AB曲線看作一條緩和曲線[2]，只要將其曲線要素計算出來，問題就解決了。

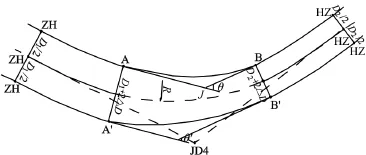
圖1 不等寬道路相對接情況示意圖

由文獻[3]知緩和曲線加寬邊線的微分方程為:

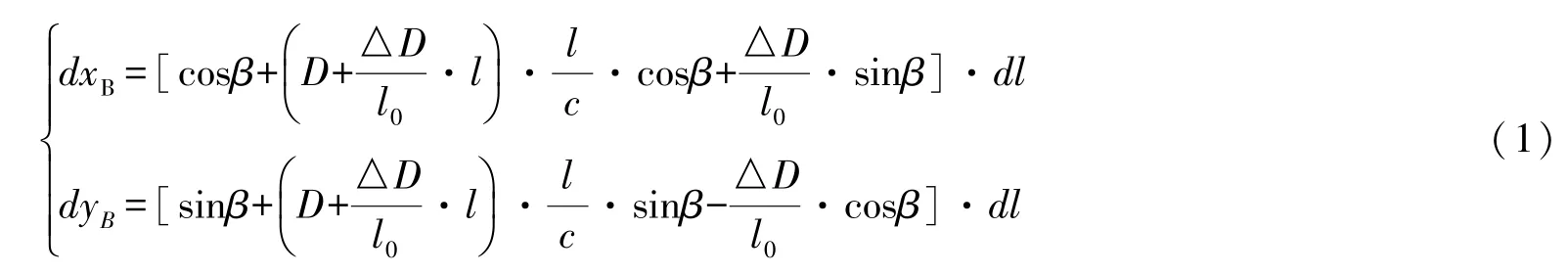
式中，β為切線角，且為緩和曲線總長，l為緩和曲線長，R為圓曲線半徑，D為道路半寬，△D為邊線加寬值(內邊線△D為負值)。

xB、yB的一階導數為:

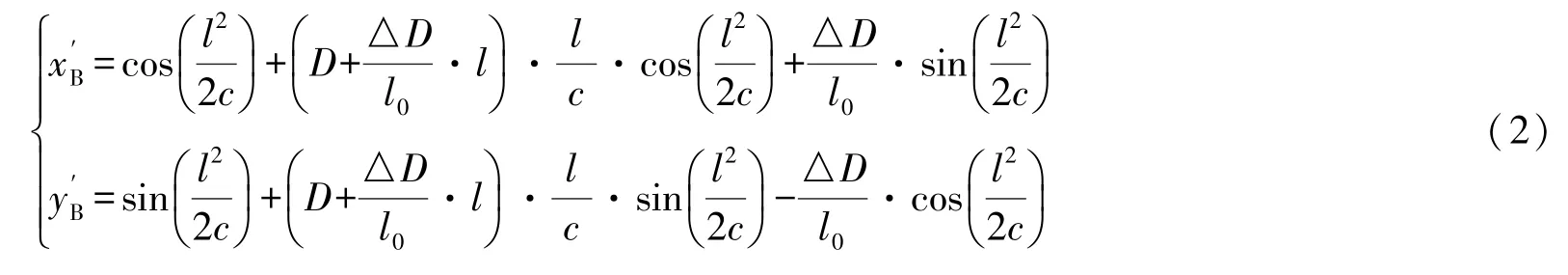
取其二階導數并整理得:

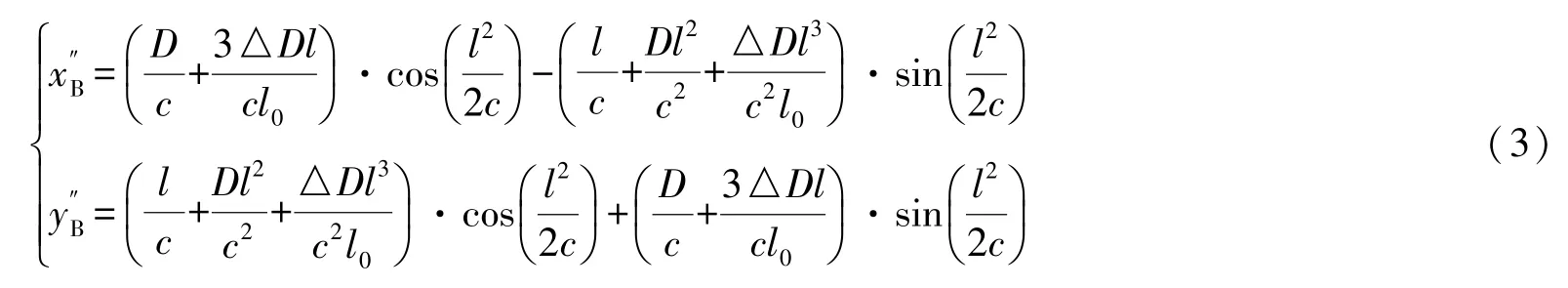
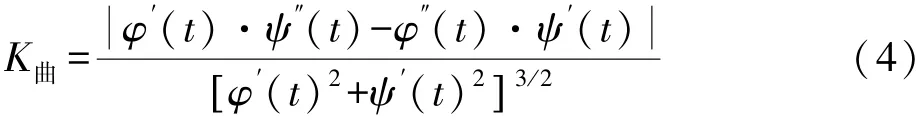
將式(2)、式(3)代入式(4)，經整理即得出求曲線在某點曲率的公式:

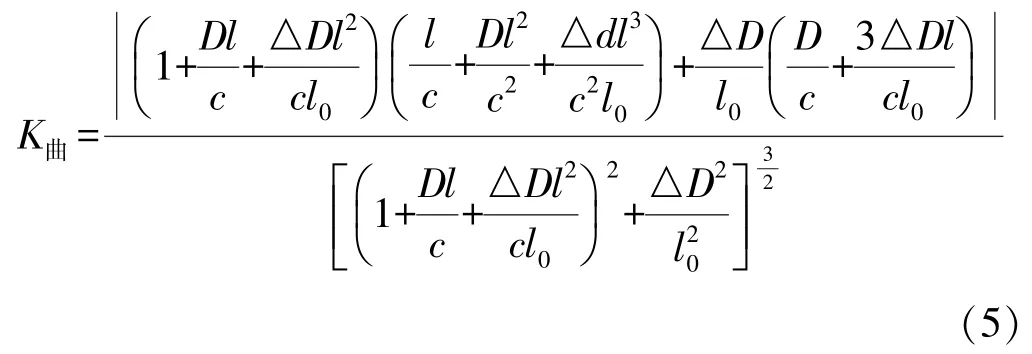
當l＝l0時，

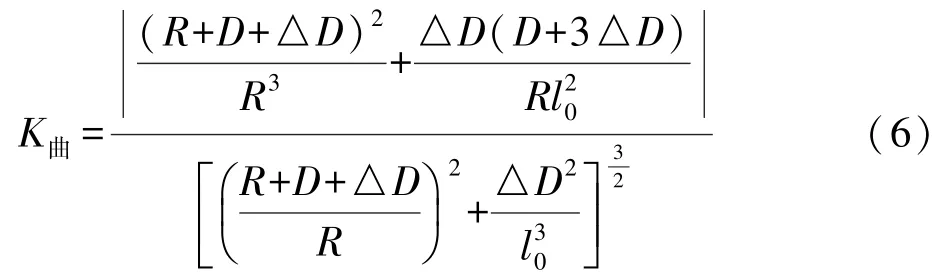
曲線的斜率為:

將式(2)代入式(6)，即得:

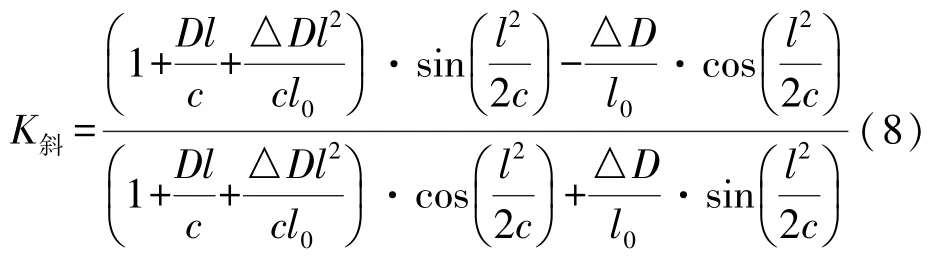
當l＝l0時，

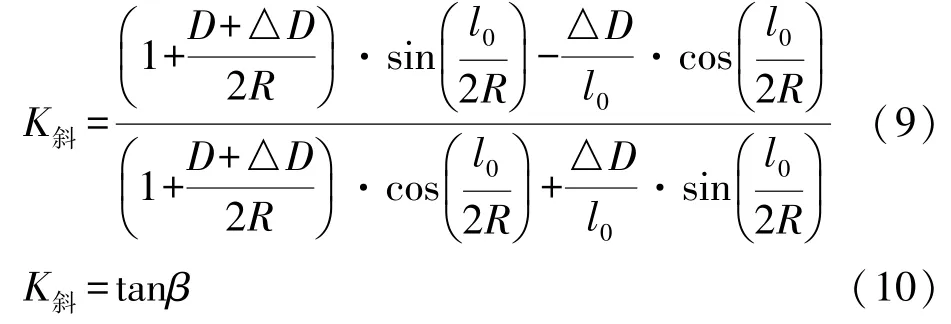
由公式(8)、(9)可分別計算出A、B兩點的切線角β1、β2，根據城市坐標即可計算出過A點和B點的切線方位角αA、αB。

如圖1所示，根據αB、αA可以求出曲線AB的轉向角θ。

由文獻[2]得曲線AB上任一點的切線角為:

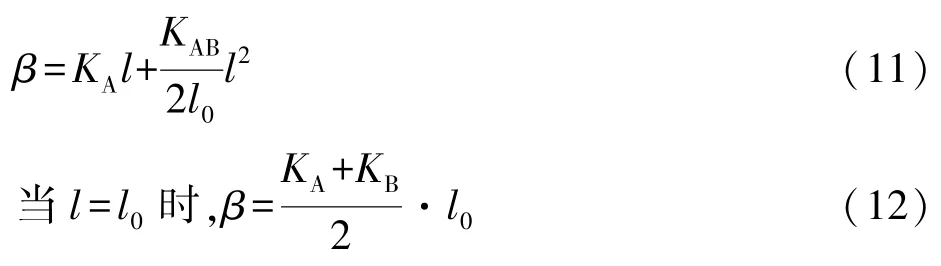
式中，l0為曲線AB的弧長，KA為曲線起點的曲率，KB為曲線終點的曲率，l為曲線上任一點距A點的弧長，KAB＝KB－KA。由式(11)可得曲線上任一點在城市坐標系中的切線方位角α，計算公式為:

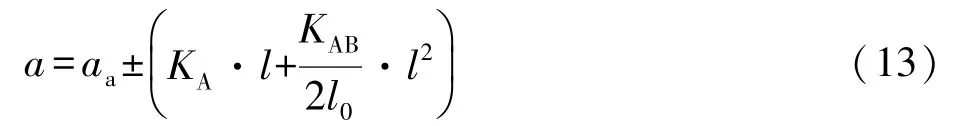
因為

將式(13)代入式(14)，積分即得曲線AB上任一點的城市坐標[5，6]:

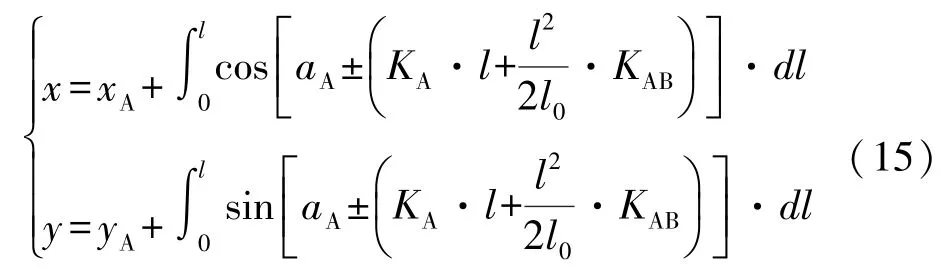
式中xA、yA為曲線起點A在城市坐標系中的坐標。

3 解算曲線要素

由式(15)可以看出，xA、yA、αA為曲線起點的城市坐標和方位角，為已知數據，KA、KB、l0為未知數。

由圖1可以看出，曲線AB的轉向角θ即為曲線AB在B點的切線角βB。

由式(12)即得:

式中，θ為弧度。

KA、KB、l0的解算采用逐漸趨近的方法。第一步:首先用公式(5)、(6)解算出A點近似曲率K′A，再代入式(16)求得K′B，l0暫由 AB的直線長代替；代入式(15)求得B點的近似坐標(x′B，y′B)；用B點近似坐標(x′B，y′B)和A點坐標xA、yA計算邊長與(xA，yA)、(xB，yB)計算的邊長進行比較，修改l0值；將修正值再代入式(15)反復計算，直到兩次計算的l0值滿足精度要求為止。

第二步:計算B′點距離過B點平行于AJ直線的垂距，利用該垂距修正A點的曲率半徑。我們可以將該垂距作為A點兩次不同曲率半徑計算B點y值的差值。下面推導曲率修改后的計算公式。

將A點作為坐標原點，A－DJ為x軸，則:

用級數將dy展開[4]

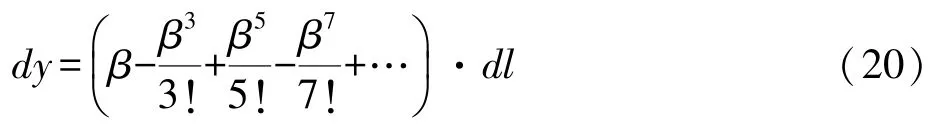
取其第一項，將式(18)代入式(20)，得

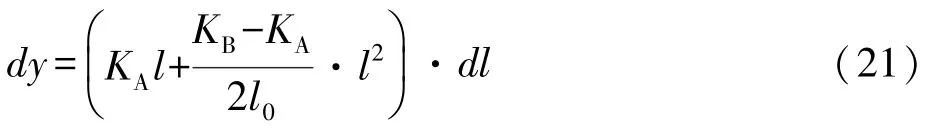
積分得

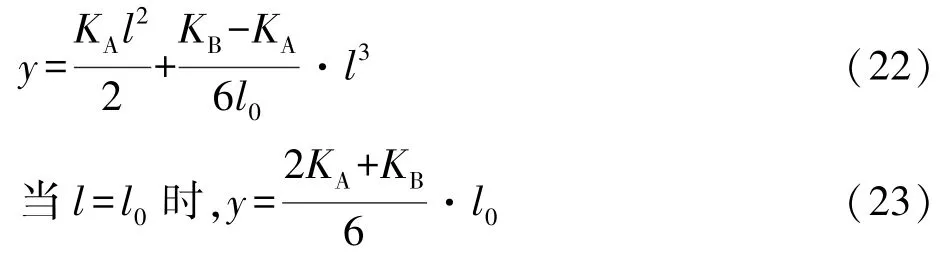
當KB曲率不變，△y引起KA曲率的變化量為

將y值的差數△y代入式(24)，即可求出KA的修正值。代入式(17)即得出新的K′B值，再進入第一步計算。

這樣進行反復計算，直到A點坐標與B點坐標計算的邊長與A點坐標與B′點坐標計算的邊長差值，及B′點到AB直線的垂距同時達到精度要求，計算即結束。

4 計算實例

上面式(15)的積分計算利用有積分功能的計算器(如CASIOfx－4800、fx－5800等)很容易計算。

舉例說明，道路JD1ZH邊線寬65 m，JD5HZ邊線寬40 m，中線為緩和曲線，曲線要素為:R＝250 m，LS1＝LS2＝110 m，內邊線緩和段加寬值為0.8 m，αZH－JD4＝77°48′14″，αHZ－JD4＝192°54′54″，算得A、B、A′、B′4點的坐標分別為436.754，計算AB曲線、A′B′曲線的要素。

用式(8)計算各點斜率，用式(10)計算切線方位角:

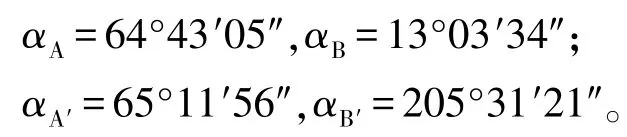
用切線方位角算出轉向角:

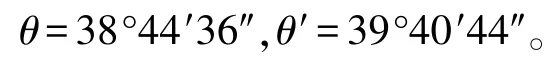
做好上述相關計算后，利用編制的計算程序即可算得:

[1]李嘉.公路設計百問[M].北京:人民交通出版社，2003，149～150

[2]工廠建設測量手冊[M].北京:測繪出版社，1990，388～390

[3]耿新田，秦延波.緩和曲線加寬邊線的解算[J].城市勘測，2008(1)

[4]同濟大學數學教研室.高等數學[M].北京:高等教育出版社，1993，180～217

[5]李全信.緩和曲線平行線的長度計算及坐標法測設[J].工程勘察，1996(3)

[6]李全信.線路中邊樁坐標計算的通用Causs－Legendre公式[J].工程勘察，2002(3)

The Method of Transition Curve Stretching for Change Width

Tian HaiYong，Geng XinTian
(Luoyang Planning＆Architectural Design Co.，Ltd.Luoyang 471000，China)

The sideline of the city－road was complex at the cross of Transition Curve.The change of width involve a lot of design procedure.This texts would expound the means and resolvent.

City－road；Transition Curve；Sideline Essential；Change Width；connecting line

1672－8262(2010)04－123－03

P258

B

2009—09—30

田海勇(1966—)，男，高級工程師，主要從事城市測繪技術管理工作。