基于博弈論的移動Ad hoc網絡入侵檢測模型

李奕男 錢志鴻 劉 影 張 旭

(吉林大學通信工程學院 長春 130025)

1 引言

隨著計算機網絡技術的不斷深入發展，移動計算設備和移動通信設備的廣泛應用，給人們在信息資源的利用和共享帶來了巨大的便利。移動Ad hoc網絡(MANET)是由一組帶有無線收發裝置的移動終端組成的多跳、臨時性自治系統，通過傳輸范圍有限的移動節點間的互相協作和自我組織保持網絡的互聯和數據傳輸。Ad hoc網絡具有無中心控制的分布性、動態變化的拓撲結構和多跳的路由結構等特性，已經廣泛的應用于軍事通信、災難救助和臨時應急會議通信等應用環境[1]。

Ad hoc網絡技術擁有廣闊的應用前景，但是由于它的無線通信信道的完全開放性和網絡拓撲結構頻繁變化缺乏穩定性，使得Ad hoc網絡更容易受到從被動監聽到主動扮演、消息重放、篡改報文和拒絕服務等各種安全威脅和攻擊[2]，因此移動Ad hoc網絡入侵檢測系統(IDS)就成為網絡安全方案的第二道防火墻。

移動Ad hoc網絡與現有的固定網絡相比有很大的差異，因此那些在傳統計算機網絡中已經廣泛應用的安全機制不再適用于移動Ad hoc網絡。入侵檢測系統的主要作用就是對整體網絡進行全面監控，實時檢測是否發生了入侵事件，并根據已有的安全策略對入侵事件進行判斷和響應。但是現有的入侵檢測手段還很有限，當攻擊者改變攻擊策略時，入侵檢測系統反應明顯滯后。同時，入侵檢測系統本身報警數量大、誤報率高的問題也很突出，使得檢測結果并不完全可信。本文將博弈理論引入到移動Ad hoc網絡的入侵檢測系統中，針對多攻擊節點和不同強度的攻擊源，建立一個非協作博弈入侵檢測模型。通過引入博弈論模型，建立攻防雙方博弈模型，本文論證了該博弈存在一個納什均衡，能夠實現網絡整體安全性的定量分析。仿真實驗表明該模型通過較小的代價換取整體網絡的安全運行，具有良好的性能指標，證明了該方法的正確性和可行性。

針對攻防雙方不對稱的網絡安全問題，Musman和Ding Yong[3,4]等人提出了靜態映射型入侵響應模型。該模型是指按一定的原則對攻擊進行分類，并用人工的方式將每一次報警映射到一個預先定義好的相應措施上。靜態映射型入侵響應很大程度上解決了人工響應長、負擔大的問題，但是當系統狀態發生變化，如網絡拓撲結構和網絡負載發生變化時，原有的響應措施將不再適應。在此基礎上，Carver和Ragsdale[5,6]等人在2000年提出了通過考慮IDS自身的誤報警率和以往響應方式的成功率來自動調整響應映射。這種動態自適應方法部分解決了響應措施的適應性問題，但是因為沒有考慮響應的代價，使得有時響應會得不償失。2002年Lee和Fan[7]等人提出了基于系統收益的入侵檢測響應模型，在綜合計算操作代價、響應代價和損失代價的基礎上選擇適當的應對策略。這種收益模型未能將不同系統遭受同一攻擊的損失不同區別開來，收益考慮的不全面。Foo和Wu[8]提出了根據IGraph圖法的基于系統收益的入侵響應和容忍模型，對系統可能的入侵路徑進行描述，然后根據入侵可能造成的系統損失和響應代價選擇響應措施。這種方法非常復雜不易實現，實用性不高。Lye和Wing[9]使用統一和隨機博弈對系統中的攻防雙方關系進行了描述和推理，證明了博弈理論對入侵檢測和響應的適用性。Xu[10]等人通過博弈理論框架來對他們提出的DDOS防御系統的性能進行分析，引導防御系統的調整。

2 移動Ad hoc網絡入侵檢測博弈模型

2.1 博弈論與網絡入侵和響應

對于分布式網絡的入侵響應而言，響應者所期望的結果或者所采取的行動，不只取決于其自身的行為(策略)，還應取決于入侵者和檢測系統的行為(策略)，而博弈論正是研究這種策略互相依存的理論。博弈論是研究競爭條件決策分析的科學，它研究的典型問題是若干個利益沖突者在同一環境中進行決策以求自己的利益得到滿足[11]。在網絡入侵和響應的過程中，入侵者的目的就是對網絡發起進攻，非法獲得網絡信息，影響正常的網絡服務；防御響應一方就是要通過實施安全策略保證網絡的正常服務。因此，入侵者和響應者之間的博弈是利益沖突的博弈，雙方都希望能夠最大化自己的利益，攻防雙方之間強調個人的理性。因此，入侵者和響應者之間的利益是完全對立的，網絡入侵和響應的過程是一個非合作、完全信息、有限次重復的對抗性博弈。

2.2 博弈模型

博弈問題有5個要素：局中人，策略空間，概率分布，信息集，效用函數。

定義 假設Ad hoc網絡中有N個節點(n=1,…,N)，則基于博弈的Ad hoc網絡入侵檢測模型如下：

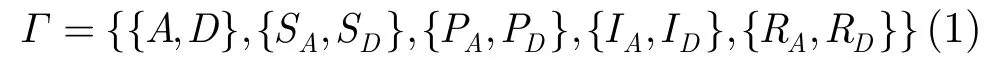
局中人：式(1)中{A, D}表示局中人，A表示網絡攻擊方，即網絡入侵者；D表示網絡防御方，即IDS的響應的決策者。

策略空間：式(1)中{SA,SD}表示局中人的策略空間，SA表示攻擊方的策略，SD表示防御方的策略。概率分布：式(1)中{PA, PD}表示探測器的概率分布矩陣，其中

信息集：式(1)中{IA,ID}表示攻擊方和防御方的信息集，信息集的維數由攻擊方采用的攻擊方式數決定。

效用函數：式(1)中{RA,RD}表示博弈模型的效用函數，代表階段博弈結束后，攻防雙方可能得到的收益集合。

2.3 模型存在納什均衡的證明

根據納什定理[12]：在一個有n個博弈方的博弈G={S1, S2,…,Sn;u1, u2,…,un}中，如果n是有限的，且Si是有限集(i=1,2,…,n)，則該博弈至少存在一個納什均衡。即每一個有限策略博弈都至少有一個混合策略納什均衡。

本模型攻防雙方的信息集維數是有限的，因此對應的策略型博弈也是有限的。根據納什均衡的存在條件，任意有限策略型博弈至少存在一個策略納什均衡。博弈中局中人都是理性的，攻防雙方只有在達到納什均衡的策略下，才能使收益最大化，也即局中人的最佳選擇。

3 仿真結果與分析

為了驗證本論文提出模型的準確性，選用了NS-2[13]軟件對模型進行仿真。實驗中引入了兩種實驗場景：(1)正常的具有入侵檢測系統的AODV路由協議；(2)引入了基于博弈論的入侵檢測的改進AODV路由協議。通過測量系統的檢測率、誤檢測率、路由包開銷和平均延遲4個主要參數指標來真實反映模型系統的安全性和穩定性。具體實驗參數設置如表1所示。實驗結果如圖1所示。

從圖1(a)和圖1(b)的仿真結果可以看出，隨著網絡中惡意節點數目的增加，大規模入侵事件的發生，IDS會產生大量警報，造成警報泛洪，從而會占用大量的通信帶寬，影響正常的網絡通信，網絡的整體性能呈現下降趨勢。本文提出的入侵檢測模型既可以提高準確率，又能夠緩解網絡擁塞的狀況。實驗證明其具有很高的檢測率，達到90%以上，誤檢率保持在10%以下，證明了方法的有效性。

表1 NS-2參數設置

從圖1(c)的仿真結果可以看出，本模型計算量少，給系統帶來的路由開銷小，占用帶寬少，節省了網絡資源。從圖1(d)中可以發現本模型計算時間短，檢測效率高，非常適宜移動Ad hoc網絡。

4 結論

本文提出了一種基于博弈論Ad hoc網絡入侵檢測模型，將攻防雙方的網絡入侵和響應的過程抽象成一個非合作、完全信息、有限次重復的對抗性博弈。在雙方的博弈過程中，尋求納什均衡，使局中人進行最佳選擇。通過實例分析和實驗可以看出，該模型能夠使IDS在響應后的收益得到保證，并且最優解穩定可靠。

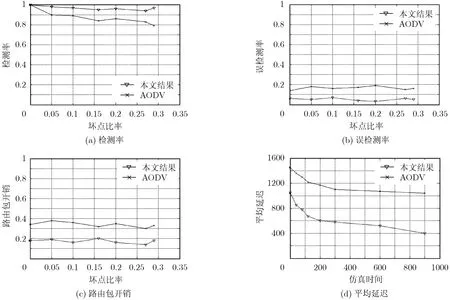
圖1 采用博弈論的入侵檢測的仿真結果

[1] 朱建明, Srinivasan Raghunathan. 基于博弈論的信息安全技術評價模型[J]. 計算機學報, 2009, 32(4): 828-834.Zhu Jian-ming and Srinivasan Raghunathan. Evaluation model of information security technologies based on game theoretic[J]. Chinese Journal of Computers, 2009, 32(4):828-834.

[2] Ryu Y U and Rhee H S. Evaluation of intrusion detection systems under a resource constraint. ACM Transactions on Information and Systems Security, 2008, 11(4): 20.1-20.24.

[3] Musman S and Flesher P. System or security managers’adaptive response tool [C]. DARPA Information Survivability Conference and Exposition 2000, Hilton Head, USA, 2000,Vol.2: 1056-1060.

[4] 丁勇, 虞平, 龔儉. 自動入侵響應系統的研究[J]. 計算機科學，2003, 30(10): 160-166.Ding Yong, Yu Ping, and Gong Jian. A study of automated intrusion response systems [J]. Computer Science, 2003,30(10): 160-166.

[5] Carver C, Hill J M, and Surdu J R. A methodology for using intelligent agents to provide automated intrusion response[C].The IEEE Systems, Man, and Cybernetics Information Assurance and Security Workshop, West Point, NY, 2000:110-116.

[6] Ragsdale D, Carver C, and Humphries J, et al.. Adaptation techniques for intrusion detection and intrusion response system[C]. The IEEE Int’l Conf on Systems, Man, and Cybernetics at Nashville, Tennessee, 2000: 1398-1406.

[7] Lee W, Fan W, and Miller M, et al.. Toward cost-sensitive modeling for intrusion detection and response [J]. Journal of Computer Security, 2002, 10(1/2): 5-22.

[8] Foo B, Wu Y, and Mao Y, et al.. ADEPTS: adaptive intrusion response using attack graphs in an E-commerce environment[C]. Int’l Conf on Dependable Systems and Networks (DSN’05), Washington, 2005: 139-146.

[9] Lye K and Wing J M. Game strategies in network security[C].The 2002 IEEE Computer Security Foundations Workshop,Copenhagan, Denmark, 2002: 71-86.

[10] Xu J and Lee W. Sustaining availability of Web services under distributed denial of service attacks [J]. IEEE Transactions on Computer, 2003, 52(4): 195-208.

[11] [美]艾里克·拉斯繆森. 王暉等譯. 博弈與信息博弈論概論. 北京: 北京大學出版社, 2003: 385-417.

[12] 董武世, 孫強, 柯宗武, 陳年生. 基于博弈論的Ad hoc網絡功率控制模型[J]. 武漢理工大學學報, 2009, 31(17): 114-122.Dong Wu-shi, Sun Qiang, Ke Zong-wu, and Chen Nian-sheng.Power control model based on game theory in Ad hoc networks[J]. Journal of Wuhan University of Technology,2009, 31(17): 114-122.

[13] Ns2 network simulation[OL]http ://www.isi.edu/nsnam/ns ,2009.