一種壓縮感知重構(gòu)算法

甘 偉 許錄平 蘇 哲

(西安電子科技大學(xué)電子工程學(xué)院 西安 710071)

1 引言

近年來出現(xiàn)了一種新穎的理論——壓縮感知[1,2](Compressed Sensing，CS)，它突破了傳統(tǒng)的奈奎斯特采樣定理，實(shí)現(xiàn)了采樣方式的轉(zhuǎn)變即從信號(hào)采樣轉(zhuǎn)變成信息采樣。CS理論有3個(gè)核心問題[3]：信號(hào)稀疏變換、觀測矩陣設(shè)計(jì)和恢復(fù)重構(gòu)算法。其中恢復(fù)重構(gòu)算法直接關(guān)系到重構(gòu)精度的大小，運(yùn)算時(shí)間的長短，決定著CS理論是否切實(shí)可行。一些學(xué)者致力于壓縮感知的恢復(fù)重構(gòu)問題提出了貝葉斯[4](BCS)，匹配追蹤[5](MP)，正交匹配追蹤[6](OMP)和分段正交匹配追蹤[7](StOMP)算法。為了提高運(yùn)算速度，另一些學(xué)者另辟蹊徑提出了梯度追蹤算法[8](GP)，但其精度較低。在GP的基礎(chǔ)上，Blumensath等人為了提高重構(gòu)精度引入了共軛方向和弱閾值原子選擇策略，提出分段弱閾值共軛梯度追蹤算法[9,10](StWCGP)，但重構(gòu)精度仍不夠理想。

針對(duì)StWCGP重構(gòu)精度比較低的缺點(diǎn)，本文在其方向和輸出上進(jìn)行改進(jìn)，明確地給出了停止迭代準(zhǔn)則。改進(jìn)后的算法稱為分段弱閾值修正共軛梯度追蹤算法(Stagewise Weak selection Modifying approximation Conjugate Gradient Pursuit,StWMCGP)。仿真結(jié)果表明StWMCGP能夠有效地提高重構(gòu)精度。

2 CS模型

CS理論指出，只要信號(hào)是可壓縮的或在某個(gè)變換域是稀疏的，那么就可以用一個(gè)與變換基不相關(guān)的觀測矩陣將變換所得的高維信號(hào)投影到一個(gè)低維空間上，然后通過求解一個(gè)優(yōu)化問題從這些少量的投影中以高概率重構(gòu)出原信號(hào)。在CS模型中并不是直接測量信號(hào)f本身，而是將信號(hào)f投影到觀測矩陣上得到觀測向量y。用矩陣表示：

式中y是M×1的觀測向量，Φ是M×N(M＜＜N)的觀測矩陣。其中信號(hào)f為長度為N的離散實(shí)值信號(hào)且在基ψ=[ψ1, ψ2,…,ψN]上是稀疏的即

式中x是N×1的系數(shù)向量且僅有k＜＜N個(gè)非零系數(shù)，ψ是N×N的稀疏矩陣。將式(2)代入式(1)得

式中A=ΦψT

為CS信息算子，其列向量稱為原子。因觀測維數(shù)M遠(yuǎn)遠(yuǎn)小于信號(hào)維數(shù)N,所以無法直接從y的M個(gè)觀測值中解出信號(hào)f。由于式(3)中x是稀疏的，這就為求解信號(hào)f提供了可能。根據(jù)信號(hào)稀疏分解理論中的稀疏分解算法，可以通過求解式(3)的逆問題解得x,然后將x代入式(2)，求得信號(hào)f。CS理論重構(gòu)問題的實(shí)質(zhì)就是在已知觀測向量y和觀測矩陣Φ的條件下，如何快速、準(zhǔn)確地重構(gòu)出信號(hào)f。

3 StWMCGP算法

3.1 傳統(tǒng)的StWCGP算法

由于OMP應(yīng)用于大尺度問題時(shí)，它所需的存儲(chǔ)空間很大且其運(yùn)算速度不夠理想，為了提高OMP的運(yùn)算速度、減少存儲(chǔ)空間，Blumensath等人提出了方向追蹤算法[8]。其流程如下：

步驟1 初始化：r0=y，x0=0，Γ0={}。

步驟2 for n=1; n=n+1直到停止條件滿足為止。

(1)gn=ATrn?1；

(2)原子下標(biāo)選取原則：in=argimax|gni|；

(3) 下標(biāo)集更新：Γn=Γn?1∪in；

(4)計(jì)算方向向量：dΓn；

(5) cn=AΓndΓn；

其中Γn表示第n次迭代時(shí)算法已選取的原子其下標(biāo)所組成的集合；AΓn表示矩陣A的子矩陣，且該子矩陣僅由那些位于下標(biāo)集Γn中的下標(biāo)所對(duì)應(yīng)的原子組成；同理：表示x的子向量，且該子向量僅由那些位于下標(biāo)集Γn中下標(biāo)所對(duì)應(yīng)的元素組成；rn表示第n次迭代時(shí)的殘余量；的元素其下標(biāo)位于集合Γn?1內(nèi)的與向量的元素完全相同，其余的為0。

StWCGP是在方向追蹤算法的框架下將第n次迭代時(shí)的方向向量取為并將原子選擇策略變?yōu)椋簗|}。其中：α表示閾值參數(shù)(α≤1)，Γ=ng表示梯度，與是G共軛的，即與的內(nèi)積為0，GΓn=的關(guān)系類似于

由于StWCGP的方向向量只取了一個(gè)與當(dāng)前方向共軛的方向，并且其輸出并不是第n次迭代時(shí)方程：=xy的最小二乘解，因此StWCGP的重構(gòu)精度并不理想。

3.2 針對(duì)StWCGP算法的改進(jìn)

StWMCGP流程如下：

步驟1 初始化：r0=y，x0=0，Γ0={}。

步驟2 for n=1；=+1 nn直到Γn中的原子下標(biāo)個(gè)數(shù)大于2k 時(shí)停止迭代。

(1)gn=ATrn?1；

(2)原子下標(biāo)選取原則：set = {i :| gi|≥ para×max |gj|} ；

(3)下標(biāo)集更新：ΓΓ?=1[set]nn；

(4) If(n=1)(n=1；n=2時(shí)都要經(jīng)過特殊處理)

(b)Γ=nncA

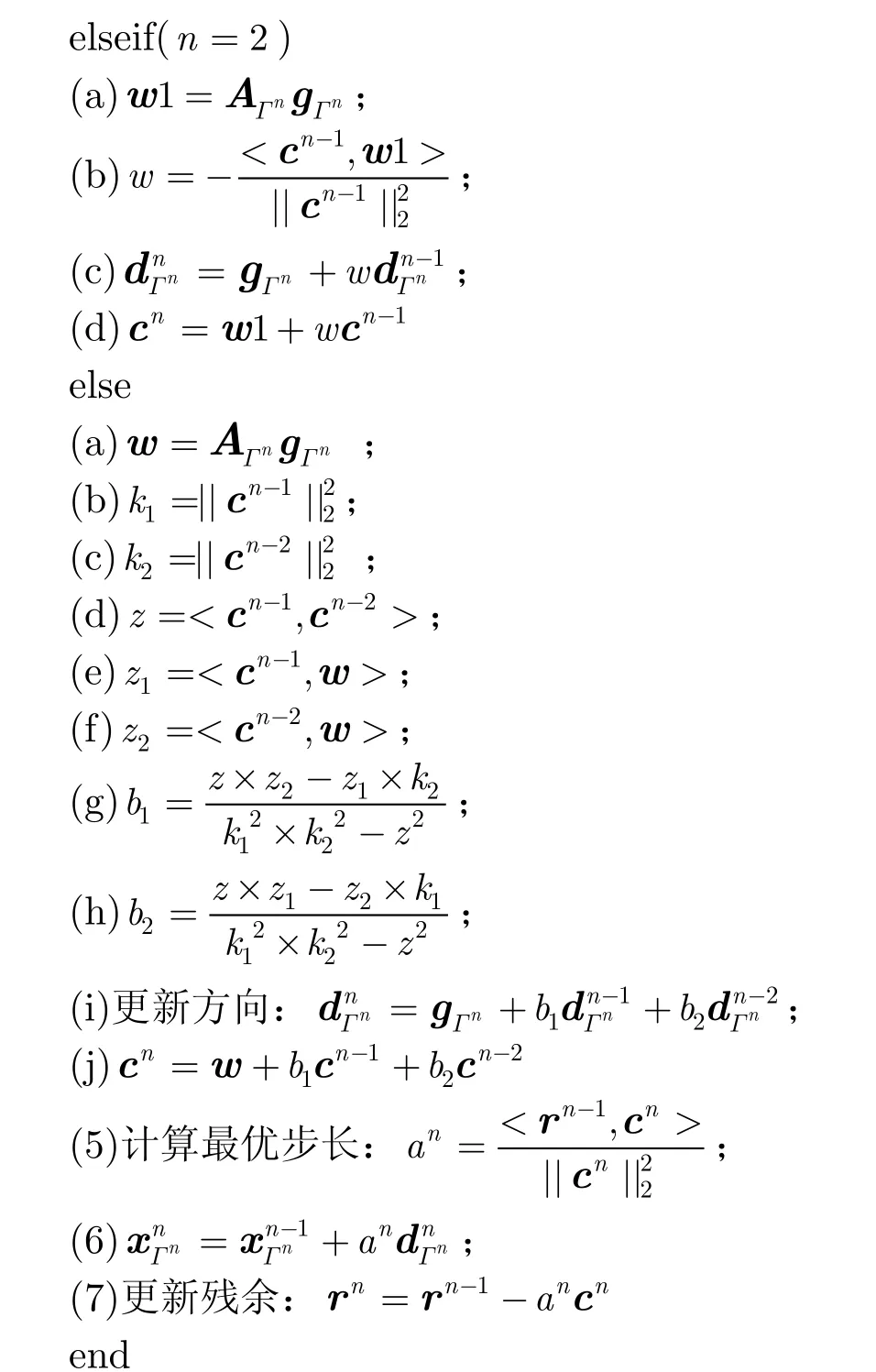
步驟3 由于Step2得到的集合Γn中可能有相同的元素，所以首先剔除集合Γn中相同的元素，得到新的集合Γn，然后采用最小二乘法反求x，此時(shí)x用x表示即

因?yàn)楫?dāng)Γn中的元素個(gè)數(shù)大于等于2k 時(shí)，Γn以很高概率包含x全部非零元素的下標(biāo)[11]。故文中將停止迭代準(zhǔn)則定義為：當(dāng)Γn中的元素個(gè)數(shù)大于等于2k 時(shí)停止迭代，其中k 代表稀疏度。由于實(shí)際中對(duì)一個(gè)稀疏信號(hào)重構(gòu)時(shí)，稀疏度是未知的，因此使用本算法首先需要對(duì)稀疏度進(jìn)行估計(jì)。本文中所有試驗(yàn)都將稀疏度k估計(jì)成N/3(經(jīng)驗(yàn)值)。

文中取兩個(gè)與當(dāng)前方向共軛的方向，是因?yàn)橄啾热?個(gè)共軛方向來講，其精度要高，僅增加了2次矩陣和向量的乘積，并且其共軛方向所對(duì)應(yīng)的系數(shù)b1，b2沒有涉及到矩陣運(yùn)算，只需在算法流程中進(jìn)行一次特殊處理。若取3個(gè)或3個(gè)以上的共軛方向，其共軛方向所對(duì)應(yīng)的系數(shù)就會(huì)涉及到矩陣的運(yùn)算，會(huì)增加計(jì)算復(fù)雜度。輸出采用x代替原來的，是因?yàn)椴皇亲钚《私狻?/p>

4 試驗(yàn)結(jié)果及分析

4.1 StWMCGP與StWCGP對(duì)稀疏信號(hào)重構(gòu)的比較

采用StWCGP和StWMCGP對(duì)長度為N=300，k=30的稀疏信號(hào)進(jìn)行重構(gòu)，觀測值數(shù)目M取150，信息算子A的各原子是從M維空間的單位球上均勻采樣而得。

由圖1(a)可以看出原稀疏信號(hào)用StWCGP在上述條件下進(jìn)行重構(gòu)，其中有3個(gè)位置不能重構(gòu)并且有些位置的圓心和十字心不重合，即這些位置沒有被精確重構(gòu)。由圖1(b)可以看出StWMCGP在同樣的條件下能對(duì)原稀疏信號(hào)實(shí)現(xiàn)精確重構(gòu)。證實(shí)了StWMCGP比StWCGP的重構(gòu)精度高。

圖1 StWCGP與StWMCGP對(duì)稀疏信號(hào)的重構(gòu)比較

4.2 不同算法精確重構(gòu)所需觀測值數(shù)目比較

從M維空間的單位球上均勻采樣得到信息算子A的各原子，以1維k 稀疏，長度為N=400的信號(hào)f為例，來測試同一稀疏度下不同算法要實(shí)現(xiàn)精確重構(gòu)對(duì)觀測值數(shù)目M(M＜N)的要求。重構(gòu)信號(hào)用來表示，當(dāng)時(shí)，重構(gòu)信號(hào)與信號(hào)f重合沒有視覺差異，認(rèn)定算法實(shí)現(xiàn)了精確重構(gòu)，其中0.004從大量的試驗(yàn)中獲得。

對(duì)同一稀疏度k，依次采用MP，StOMP-FAR[7]，StOMP-FDR[7]，BCS，StWMCGP對(duì)信號(hào)f進(jìn)行重構(gòu)，記錄下剛好精確重構(gòu)時(shí)的M，其中MP的最大迭代次數(shù)maxIter設(shè)為10000次；StOMP-FDR算法中最大迭代次數(shù)S=30，參數(shù)q=0.9；BCS中參數(shù)sigma=y的方差/100；StWMCGP中參數(shù)para=0.98。StOMP-FAR中的最大迭代次數(shù)S=10、參數(shù)q=M/(NS)(1?k/N)，式中M表示A的行數(shù)，N表示A的列數(shù)，k是稀疏度，S是最大迭代次數(shù)。

從圖2可知：對(duì)于長度為N=400的信號(hào)當(dāng)稀疏度小于120時(shí)，StWMCGP實(shí)現(xiàn)精確重構(gòu)所需的觀測值數(shù)目最少且比MP，StOMP-FDR所需的觀測值個(gè)數(shù)少20%，比BCS，StOMP-FAR少3%。證實(shí)了相同的觀測值個(gè)數(shù)條件下，StWMCGP的重構(gòu)精度最高。綜上可知：實(shí)際應(yīng)用中采用StWMCGP對(duì)信號(hào)進(jìn)行重構(gòu)是理想的選擇。

圖2 精確重構(gòu)時(shí)稀疏度k與觀測值數(shù)目M之間的關(guān)系曲線

4.3 StWMCGP算法對(duì)2維圖像的處理

本實(shí)驗(yàn)以圖像Mondrian為例其大小為512×512。為了與以往經(jīng)典算法進(jìn)行對(duì)比，仍然采用小波基“symmlet8”，將Mondrian在該基下進(jìn)行展開。采用多尺度CS[4]來對(duì)該圖像進(jìn)行重構(gòu)，其中粗尺度j0設(shè)為4，細(xì)尺度j設(shè)為6，信息算子A的各原子是從M維空間的單位球上均勻采樣而得。圖3(a)是原圖像；圖3(b)是采用小波變換得到的圖像，所用樣本數(shù)K=4096；圖3(c)是采用StOMP-FDR進(jìn)行多尺度重構(gòu)后的圖像，所用樣本數(shù)為K=2713，參數(shù)q=0.9，最大迭代次數(shù)S=30；圖3(d)是采用StOMP-FAR進(jìn)行多尺度重構(gòu)后的圖像，所用樣本數(shù)K=2713，參數(shù)q=0.4M/NS ，最大迭代次數(shù)S=30；圖3(e)是采用BCS進(jìn)行多尺度重構(gòu)后的圖像，所用樣本數(shù)K=2713，參數(shù)sigma= y的方差/100；圖3(f)是采用StWMCGP進(jìn)行多尺度重構(gòu)后的圖像，所用樣本數(shù)K=2713，參數(shù)para=0.95。各個(gè)算法的運(yùn)算時(shí)間和重構(gòu)精度見表1，其中重構(gòu)精度以相對(duì)誤差作為參考：其中f代表原圖像信號(hào)，f代表重構(gòu)信號(hào)。

圖3 不同算法對(duì)Mondrian的重構(gòu)比較

由表1可知：參數(shù)para=0.9時(shí)StWMCGP的運(yùn)算時(shí)間最短，此時(shí)其重構(gòu)精度與StOMP-FAR相當(dāng)，參數(shù)para=0.95時(shí)StWMCGP的重構(gòu)精度最高，此時(shí)的運(yùn)算時(shí)間與BCS相當(dāng)。StWMCGP對(duì)于不同參數(shù)para運(yùn)算時(shí)間和重構(gòu)精度不同，主要在于參數(shù)para越大，StWMCGP每次迭代所選原子就越少，那么錯(cuò)選原子的概率就會(huì)降低，迭代次數(shù)就會(huì)增多，這樣便增加了重構(gòu)精度但也增加了運(yùn)算時(shí)間；相反參數(shù)para越小，每次迭代所選原子就越多，那么選錯(cuò)原子的概率就會(huì)增加，迭代的次數(shù)就會(huì)減少，這樣便減少了運(yùn)算時(shí)間但也降低了重構(gòu)精度。所以在處理具體問題時(shí)，可通過選擇參數(shù)para來決定是增加重構(gòu)精度還是提高運(yùn)算速度。由表1和圖3可知：小波變換過于平滑且存在偽邊緣，重構(gòu)精度最差。用StOMP-FDR重構(gòu)效果也比較差；而用StOMPFAR，BCS，StWMCGP重構(gòu)從視覺上來講沒有太大差異，但StWMCGP的重構(gòu)精度最高。

5 結(jié)論

針對(duì)StWCGP重構(gòu)精度比較低的特點(diǎn)本文提出了StWMCGP，仿真結(jié)果表明該算法的重構(gòu)精度比StWCGP，MP，StOMP-FDR高，也比StOMPFAR，BCS略高；并在重構(gòu)精度可接受的情況下，通過調(diào)節(jié)參數(shù)還能提高運(yùn)算速度。

表1 不同算法運(yùn)算時(shí)間和重構(gòu)精度(相對(duì)誤差)

[1] Candès E, Romberg J, and Tao Terence. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[3] 石光明，劉丹華, 等. 壓縮感知理論及研究進(jìn)展[J]. 電子學(xué)報(bào)，2009, 37(5): 1070-1081.Shi Guang-ming and Liu Dan-hua, et al.. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081.

[4] Ji Shi-hao, Xue Ya, and Carin L. Bayesian compressive sensing[J]. IEEE Transactions Signal Processing, 2008, 56(6):2346-2356.

[5] Mallat S and Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[6] Tropp J and Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655-4666.

[7] Donoho D L, Tsaig Y, Drori I, and Starck J L. Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit. (Preprint, 2007) http:// www.dsp.ece.rice.edu/cs.

[8] Blumensath T and Davies M E. Gradient pursuits[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2370-2382.

[9] Blumensath T and Davies M E. Stagewise weak gradient pursuits. Part I Fundamentals and numerical studies.(Preprint, 2008) http://www.dsp.ece.rice.edu/cs.

[10] Blumensath T and Davies M E. Stagewise weak gradient pursuits. Part II Theoretical properties. (Preprint, 2008)http://www.dsp.ece.rice.edu/cs.

[11] Needell D and Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[OL]. 2007, http:// www. math. ucdavis. edu/～vershynin/papers/ROMP. pdf .