基于直方圖插值的均值移動小尺寸目標跟蹤算法

陳建軍 安國成 張索非 吳鎮揚

①(東南大學信息科學與工程學院 南京 210096)②(中國科學院軟件所人機交互技術與智能信息處理實驗室 北京 100190)

1 引言

視覺跟蹤技術自動檢測和跟蹤視頻序列中的目標，估計目標的運動參數和運動狀態。其在智能視頻監控、友好人機交互、基于內容的視頻檢索和壓縮、視頻會議和大型活動安防等領域中應用廣泛。

在遠距離室外視頻監控和點光源跟蹤等應用中都會遇到小尺寸目標跟蹤的問題[1]。有時也會把大尺寸目標分成多個小區域，分別跟蹤各區域的低維運動參數(如位移)，再將所有跟蹤結果融合起來估計目標整體的高維運動參數(如位移、尺寸和旋轉等)[2]。小尺寸目標包含的像素非常少，而其外表特征又很容易發生變化，所以很難用傳統的方法來跟蹤它們。近幾年，研究人員提出了很多小目標的檢測和跟蹤算法[3,4]。Formont等人[3]使用非線性最優濾波器，提出了基于自適應相關的小目標跟蹤算法。Wang等人[4]研究了海面上小尺寸運動目標的檢測和跟蹤問題。他們把背景相減法和對稱差分法結合起來檢測目標，使用均值移動和卡爾曼濾波來跟蹤目標。

近幾年，均值移動算法在視覺跟蹤中得到廣泛應用[5?12]，其原理簡單，實時性能優越。均值移動是在1975年由Fukunaga等人[5]在非參概率密度估計中求解概率密度的極值問題而提出，當時并沒有受到人們的重視。直到1995年，Cheng對均值移動迭代算法加以推廣，并應用于聚類分析中[6]，引起研究人員的關注。Comaniciu在將均值移動算法應用于視頻目標跟蹤方面做了大量工作，提出了魯棒高效的均值移動視覺跟蹤算法[7]。隨后對均值移動算法的研究基本是在他提出框架下進行的。近年來，有學者在跟蹤特征的選擇，直方圖單元的劃分等方面對其加以改進。Bajramovic等人[8]采用多種不同特征，把各種特征的直方圖加權組合作為跟蹤線索，使用均值移動和信賴域優化方法跟蹤目標。Li等人應用均值移動算法的聚類功能自適應劃分顏色空間，并用獨立分量分析(ICA)對每個單元內的顏色分布進行建模[9]。Chu等人使用最大模糊熵高斯聚類算法將觀測點加入到跟蹤窗中，并把Kalman濾波與均值移動算法相結合來快速跟蹤目標[10]。Li等分別使用背景加權直方圖和顏色加權直方圖來表示目標模型和候選目標，可以自適應地獲得目標尺寸，通過由粗到細的方法實現均值移動尋找全局極大值點，減少了所需的迭代次數[11]。

本文使用均值移動算法來跟蹤小尺寸目標。論文首先對均值移動算法在跟蹤小尺寸目標中計算權值時容易出現的除以零問題進行了分析，并指出了其一般處理方法所導致的跟蹤中斷問題；然后將Parzen窗密度估計方法加以改進，并用來對候選目標區域的直方圖進行插值；本文采用Kullback-Leibler距離來度量目標模型和候選目標的相似性，增加了度量的可分辨性，提高了算法的跟蹤精度和魯棒性。論文在多段視頻中跟蹤目標，結果表明，本文提出的算法可以有效地跟蹤只有6×12個像素的小目標。

2 均值移動算法跟蹤小尺寸目標的主要問題

2.1算法跟蹤中斷問題

均值移動在當前幀中跟蹤目標時，需要按照下式[7]迭代計算新位置y1

其中xi是以y0為中心，h為帶寬的核窗內的像素坐標；g(?)為核函數的影子函數；這里權值ωi的計算公式為

其中qu和pu(y0), u=1,…, m分別為目標模型和y0處候選目標的直方圖；b(xi)是點xi所在直方圖單元的指示函數。

可見均值移動算法需要把目標模型和候選目標的相應直方圖單元qu和pu(y0)相除來計算權值ωi。小尺寸目標包含的像素很少，因此其直方圖中只有很少單元有非零值，絕大部分的數值都為零。當pu取值為零時，就會出現除以零問題。文獻中的一般處理方法是[7]：如果像素xi所對應的直方圖單元pu=0，則將其權值設置為零，即ωi=0。在跟蹤過程中，受外部環境變化和目標自身運動等因素的影響，目標顏色值會發生變化，從而引起候選目標直方圖分布的變化。當對于核窗內所有像素xi，qu和pu(y0)的非零單元都不重疊時，即qu* pu(y0)=0,u=1,…,m，得到的所有權值ωi都為零。這樣式(1)就是零除以零運算，計算的目標新位置為奇異值，從而導致跟蹤中斷。

2.2 跟蹤目標丟失問題

在均值移動跟蹤算法中，目標模型與候選目標之間的相似性度量函數非常重要，它決定了在計算新位置時各個像素的權值大小。目前常用的均值移動算法[7,8]把Bhattacharyya系數作為相似性度量函數：

可以看出在Bhattacharyya系數中，目標模型和候選目標的作用是平等的。但是在跟蹤過程中，目標模型是固定的(如果不更新模板)，而候選目標區域卻是時刻變化的。所以把目標模型和候選目標的作用等同起來是不合適的，會降低算法的跟蹤精度和魯棒性，從而導致丟失跟蹤目標。另外Bhattacharyya系數還有辨別能力弱，計算量按樣本數量的平方增長等缺點[12]。

3 基于直方圖插值的改進算法

3.1 直方圖插值

式中c為歸一化常數，δ(?)為Kronecker delta函數，b()是點所在直方圖單元的指示函數。

如前所述，小尺寸目標的像素少，易使候選目標與目標模型不匹配，導致跟蹤中斷。一些傳統的數值處理手段和模板更新等可以在一定程度上解決這個問題。但是模板更新面臨著更新時機難確定，易把背景像素引入模板中，算法實現復雜等問題。本文使用一種簡單有效的直方圖插值方法來解決這個問題。本文用Parzen窗法對候選目標的直方圖進行插值。Parzen窗法是一種常用的非參概率密度估計方法，其由Parzen于1962年提出[13]。對于n個d維訓練樣本U={u1,u2,…,un}，Parzen窗密度估計法為[14]

其中?(?)是非負窗函數；hn是窗口尺寸。

可以看出原Parzen窗法沒有利用插值直方圖單元u周圍單元的信息，所以原Parzen窗法不能直接應用到本文的直方圖插值處理中。本文對原算法進行改進，得到新的基于Parzen窗的直方圖插值處理方法為

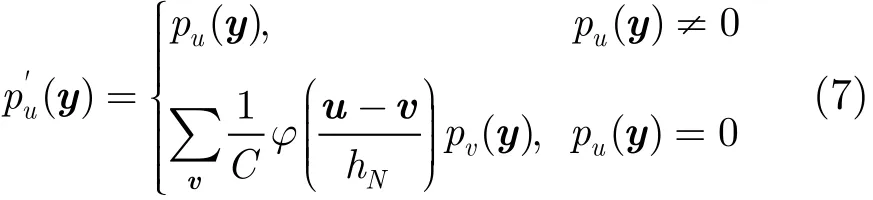
其中v是窗?(?)中所包含的直方圖單元的索引值；hN是插值窗函數的帶寬；C是歸一化系數，其是要保證所以有C=

經過直方圖插值處理的結果如圖1所示。本文選擇在歸一化rg顏色空間中建立直方圖，其中rg劃分的單元數為64×64。圖1(a)是視頻序列中的一幀圖像以及目標區域(6×12)。圖1(b)是目標區域的直方圖，可見由于目標包含的像素很少，只有極少直方圖單元有非零值。圖1(c)是使用改進直方圖插值方法得到的直方圖。可以看出，原非零值單元的數值未發生變化，而這些單元附近的原零值單元有了較小數值。這樣既沒有對真實直方圖的數值分布產生很大影響，又給目標顏色區域的單元賦予了一定數值，有效地解決了權值計算中的除以零問題。

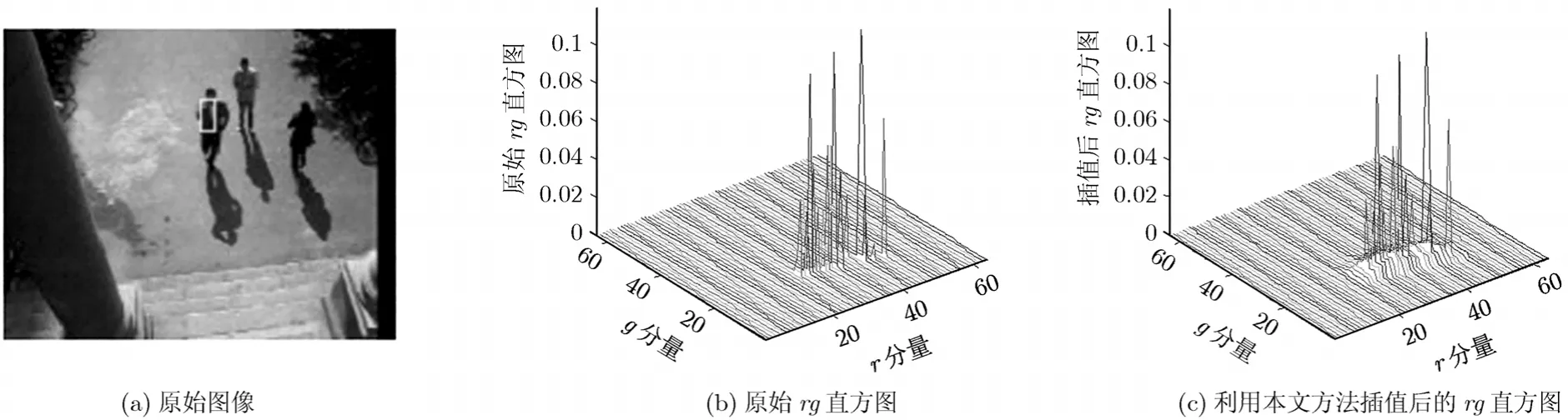
圖1 直方圖插值處理結果

3.2 相似性度量函數

建立了目標模型和候選目標的顏色直方圖，就可以度量兩者之間的相似性。相似性度量函數的選擇非常重要，其直接影響著算法的跟蹤精度和魯棒性。本文采用Kullback-Leibler距離代替Bhattacharyya系數來度量兩者之間的相似性，即有

用Bhattacharyya系數和Kullback-Leibler距離來度量不同距離的結果如圖2所示。假設qu是服從均值為10，方差為1的高斯分布；而(y)是均值從0變到10，方差為1的高斯分布。圖中橫坐標為(y)的均值，縱坐標為兩者之間的距離。可以看出隨著兩個分布越來越接近，Bhattacharyya系數反映了兩者的相似程度，因此其逐漸增大；Kullback-Leibler距離是度量兩者之間的區別，所以其逐漸減小。后者比前者的變化范圍大，這就意味著其有更強的辨別能力，可以更好地區分目標模型和候選目標。

3.3 跟蹤算法

圖2 兩個分布之間的不同距離度量

其中權值ωi的計算公式為

式(9)右邊的前兩項是常數，與y的值無關，因此要使ρ(y)最小，只要使等式右邊的第3項最大。可以看出該項是在給各像素xi賦予了權值ωi之后，基于核函數k(?)估計的y處的概率密度，因此可以用均值移動算法來計算ρ(y)的極值點。ρ(y)不斷迭代從當前位置y0移動到新位置y1，就能夠以最快的速度收斂到極值點，這里的新位置迭代公式為

其中g(x)=?k'(x)，這里假設k(x)在x∈[0,∞)上的導數總是存在。

新算法與傳統均值移動算法的主要區別在于權值ωi的不同(式(2)和式(10))。在跟蹤過程中，目標模型是由檢測或手工標注得到的，通常比較準確，因此其直方圖中目標顏色分量較多，對應直方圖單元的數值比較大，非目標顏色單元的數值較小。對還沒有跟蹤到目標真實位置的候選目標區域而言，情況恰恰相反，其包含的背景區域相對較多，因此目標顏色分量對應直方圖單元的數值較小，而非目標顏色分量對應單元的數值較大。因此由式(10)計算的權值總體上是目標區域像素的權值大于1，而非目標區域像素的權值小于1。而傳統均值移動算法在計算權值時要在式(10)的基礎再做開方運算，這樣會減小目標區域像素的權值，增大非目標區域像素的權值，縮小權值的變化范圍。這樣就不能很好地區分目標和非目標區域，影響算法的跟蹤精度。另一方面，新權值無需做開方運算，減少了算法的計算量。

本文選擇Epanechnikov核，則y1的計算公式可以簡化為

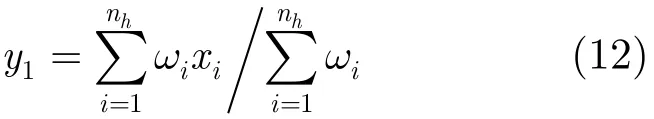
在給出以上準備工作之后，將本文提出的基于直方圖插值處理和新型度量函數的均值移動小尺寸目標跟蹤算法的主要流程總結如下：

給定目標模型的顏色直方圖{qu}；目標在上一幀中的位置y0。

(1)初始化目標在當前幀中的位置y0，并計算以y0為中心的候選目標的核顏色直方圖{pu(y0)}；

(2)通過檢查候選目標{pu(y0)}與目標模型{qu}是否有非零單元重疊來判斷兩者是否匹配：如果匹配轉到步驟(4)繼續跟蹤；否則轉到步驟(3)進行直方圖插值處理；

(3)用式(7)對候選目標的直方圖{pu(y0)}進行插值處理，得到插值后的直方圖{(y)}；0

(4)根據新型權值計算式(10)計算各像素的權值{ωi}, i=1,…,nh；

(5)按照位置更新公式(12)計算候選目標的新位置y1；

(6)判斷如果‖y1－y0‖＜ω，則停止迭代，并令y0＝y1，輸出目標在當前幀中的位置，讀入下一幀，開始新的跟蹤；否則，賦值y0＝y1，返回到步驟(1)，繼續迭代跟蹤。

4 實驗結果

本文所提算法在多段視頻中進行測試，這里給出部分結果。rg顏色空間被劃分為64×64個單元；直方圖插值選擇高斯窗，窗函數帶寬hN為10；算法的最大迭代次數為15次；迭代終止門限ω為1個像素。初始幀中的目標真實位置是由手工標注的。

表1給出了基本均值移動算法(Traditional Mean Shift，TMS)和本文的基于直方圖插值的均值移動算法(Histogram Interpolation-based Mean Shift，HIMS)對視頻序列的總體跟蹤性能。表中列出了3段視頻序列的跟蹤結果。目標的真實位置由手工標注。在每幀中對目標區域標注3次，然后求其平均值作為真實值。如果連續兩次標注的誤差超過某個閾值(標注誤差)，則重新標注該幀圖像。X誤差和Y誤差分別表示在X，Y方向上的誤差。在每幀中，如果跟蹤的目標中心落在手工標注的目標區域內，則認為跟蹤成功，否則認為跟蹤失敗。整段視頻的跟蹤率定義為全部成功跟蹤的幀數除以該序列的總幀數，即

表1 算法跟蹤的總體性能比較

從表中可以看出：除序列OurSeq_001的Y方向平均誤差之外，本文所提的HIMS算法對所有序列跟蹤的X，Y方向誤差的均值和標準差都小于TMS算法。這說明HIMS比TMS跟蹤的更加準確，而且跟蹤更加穩定，算法魯棒性更高。HIMS的跟蹤率也明顯高于TMS。

4.1 跟蹤中斷問題

序列OurSeq_001共有751幀，每幀大小為160×120，目標尺寸為8×16。目標有轉圈、停留、轉身等動作，而且運動到樹蔭區域。圖3給出了兩種算法的跟蹤結果。TMS在第175，253和532幀時跟蹤中斷，在第541，550，570，587和711幀時丟失目標。HIMS能夠一直跟蹤目標。圖4是TMS和HIMS的跟蹤誤差。圖中橫坐標是幀標號，縱坐標是歐氏距離誤差(像素)。圖中實線和虛線分別是TMS算法和HIMS算法的跟蹤誤差(后面同)。TMS跟蹤失敗的次數較多，多次重新開始跟蹤，相當于進行模板更新。但其在中斷幀處產生非常大的誤差，而且在后續幀中的誤差也變化較大。HIMS的跟蹤誤差大多在5個像素以內，而且比較穩定，有效地解決了除以零運算問題，提高了算法的魯棒性。

4.2 跟蹤目標丟失問題

CAVIAR項目[15]視頻是監控類視頻，主要用于目標行為識別和分析。序列Fight_OneManDown(FOMD)中跟蹤目標出現在第168幀到436幀共269幀中，每幀大小為384×288，目標尺寸為14×16。目標與他人打斗，并將對方打倒在地，然后逃竄。目標運動較快，動作幅度較大，而且目標上衣顏色與地面顏色非常接近，因此跟蹤難度很大。圖5給出了兩種算法的跟蹤結果。TMS在第181，297，436幀時丟失目標。HIMS可以始終跟蹤目標。圖6給出了TMS和HIMS的跟蹤誤差。在第296幀之前，HIMS跟蹤的更加準確；之后目標直線快速奔跑，兩種算法的跟蹤精度差別不是很明顯。

4.3 算法整體性能驗證

序列OurSeq_002既有多次跟蹤中斷，也有多次丟失跟蹤目標，因此其可以用來驗證直方圖插值和新型相似性度量函數的總體性能。序列共有683幀，目標出現在第196幀到第524幀共329幀中，每幀大小為160×120，目標尺寸為6×12。目標在光照有較大變化的區域內行走，且有部分遮擋。圖7給出了TMS和HIMS的跟蹤結果。由于目標的尺寸非常小，而且光照變化較大，TMS在第219，311，331，367，384，387，425和471幀跟蹤中斷，在第295，302，478，500和520幀丟失跟蹤目標；HIMS可以一直跟蹤目標。圖8給出了兩種算法的跟蹤誤差。可以看出，HIMS的跟蹤誤差基本都在5個像素以內；TMS算法多次發生跟蹤中斷和丟失跟蹤目標，因此其跟蹤誤差波動較大。

圖3 對序列OurSeq_001的跟蹤結果，依次是第53，291，541，570，587，711幀

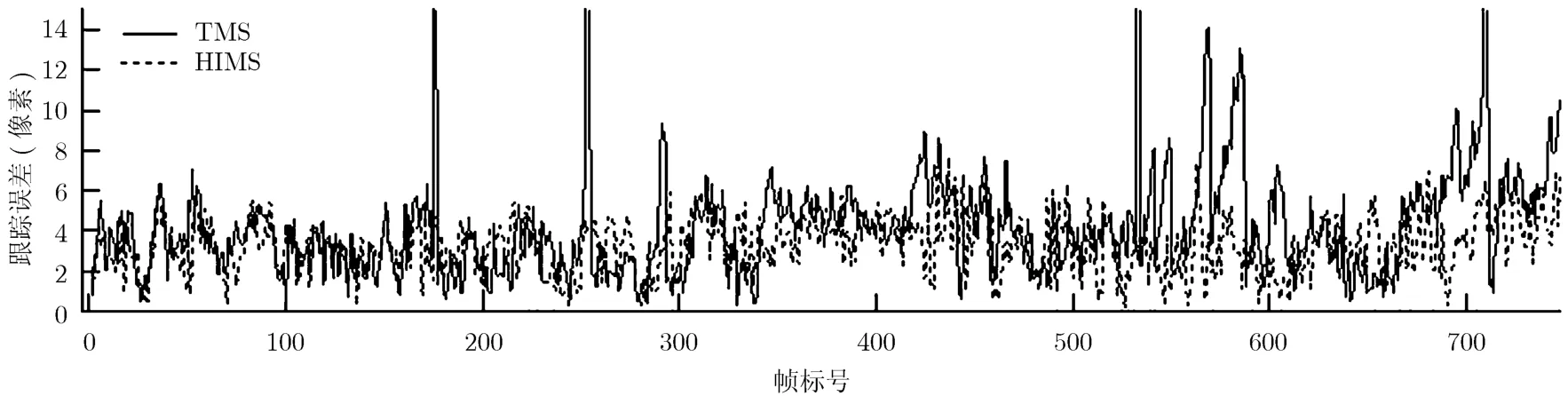
圖4 對序列OurSeq_001的跟蹤誤差

圖5 對序列FOMD的跟蹤結果，依次是第181，265，297，436幀

圖6 對序列FOMD的跟蹤誤差

圖7 對序列OurSeq_002的跟蹤結果，依次是第219，295，302，478，500，520幀

圖8 對序列OurSeq_002的跟蹤誤差

5 結論

本文提出了一種基于直方圖插值處理的均值移動小尺寸目標跟蹤算法。論文分析了均值移動算法權值計算中的除以零問題和其一般處理方法，以及其所導致的跟蹤中斷問題。論文提出在候選目標與目標模型不匹配時，對候選目標的直方圖進行插值處理來增加其非零單元數，然后再用均值移動進行跟蹤。此外論文還選用Kullback-Leibler距離來度量目標模型和候選目標的相似性。實驗結果表明，本文所提算法可以有效地跟蹤小尺寸目標，算法的跟蹤精度也有一定提高。

[1] Kaewtrakulpong P and Bowden R. A real time adaptive visual surveillance system for tracking low-resolution colour targets in dynamically changing scenes [J]. Image and Vision Computing, 2003, 21(10): 913-929.

[2] Han B and Davis L S. Probabilistic fusion-based parameter estimation for visual tracking [J]. Computer Vision and Image Understanding, 2009, 113(4): 435-445.

[3] Formont S, Laude V, and Refregier P. Small target tracking on image sequence using nonlinear optimal filtering [C].Signal and Data Processing of Small Targets, 1995. San Diego,CA, USA, SPIE, 1995, 2561: 299-307.

[4] Wang L, Hu S, and Zhang X. Detecting and tracking of small moving target under the background of sea level [C]. The 9th International Conference on Signal Processing, ICSP'2008,Beijing, China, 2008: 989-992.

[5] Fukunaga K and Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1):32-40.

[6] Yizong C. Mean shift, mode seeking, and clustering [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1995, 17(8): 790-799.

[7] Comaniciu D, Ramesh V, and Meer P. Kernel-based object tracking [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564-577.

[8] Bajramovic F, Gr C, and Denzler J. Efficient combination of histograms for real-time tracking using mean-shift and trust-region optimization [C]. The 27th Symposium on German Association for Pattern Recognition, DAGM2005,Vienna, Austria, Springer Verlag, 2005, 3663: 254-261.

[9] Li P. An Adaptive Binning Color Model for Mean Shift Tracking [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(9): 1293-1299.

[10] Hongxia C and Wang K. Target tracking based on mean shift and improved kalman filtering algorithm [C]. IEEE International Conference on Automation and Logistics, ICAL'09. Shenyang, China, 2009: 808-812.

[11] Li S X, Chang H X, and Zhu C F. Adaptive pyramid mean shift for global real-time visual tracking [J]. Image and Vision Computing, 2010, 28(3): 424-437.

[12] Yang C, Duraiswami R, and Davis L. Efficient mean-shift tracking via a new similarity measure [C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR '2005. San Diego, CA, United states,2005: 176-183.

[13] Parzen E. On estimation of a probability density function and mode [J]. Annals of Mathematical Statistics, 1962, 33(3):1065-1076.

[14] Shen H and Yan X. Probability density estimation over evolving data streams using tilted Parzen window [C]. IEEE Symposium on Computers and Communications, ISCC'2008,Marrakech, 2008: 585-589.

[15] CAVIAR: EU funded project, IST 2001 37540, URL:http://homepages.inf.ed.ac.uk/rbf/CAVIAR/(2004).