基于排隊時延和丟包率的擁塞控制

謝 鈞 俞 璐 金鳳林

①(解放軍理工大學指揮自動化學院 南京 210007)

②(解放軍理工大學通信工程學院 南京 210007)

1 引言

擁塞控制是保證網絡穩定運行的重要手段，其基本方法是發送方根據從網絡獲得的擁塞反饋信息調整發送速率。網絡鏈路可為發送方提供顯式或隱式的擁塞指示，TCP及其各類改進算法通常不需要鏈路提供顯式的擁塞指示。如果路由器不主動提供顯式的擁塞指示，發送源只能利用丟包事件和往返時延/排隊時延作為反饋信息。擁塞控制算法按照采用的擁塞指示信息可分為基于丟包和基于時延的擁塞控制。基于丟包的擁塞控制算法除當前的TCP(Reno)外，還有HS-TCP[1]，E-TCP[2]，CUBIC[3]等，而基于時延的擁塞控制算法主要有FAST TCP[4]，TCP Vegas[5]，BIC-TCP[6]，文獻[7]等。

作為擁塞反饋，與丟包率相比，排隊時延本身就是多比特信息，通常更易測量，因此基于時延的模型通常能比基于丟包信息的模型獲得更加平滑的吞吐量[4]。另外，基于排隊時延的擁塞控制算法可避免或盡量減少網絡中丟包事件的發生，起到一定的擁塞避免的作用。在基于時延的擁塞控制算法中，近年來提出的FAST TCP充分發揮了利用排隊時延作為反饋信息的上述優點，在大帶寬-時延積的網絡中可獲得穩定的流動態性，對不同RTT(Round-Trip Time)的異構流具有加權成比例公平性。由于FAST TCP的優良特性，近年來出現了大量相關研究[8?11]。FAST TCP以排隊時延作為擁塞量度，控制發送速率使各流在瓶頸鏈路緩存中的分組維持在一個適當的數目，從而各異構流公平共享瓶頸帶寬。但FAST TCP存在一個難以克服的問題，即當路徑中的路由器緩存不夠大時，共享瓶頸鏈路的流在到達平衡點前會遭遇丟包。此時FAST仍然要采用類似AIMD的算法，從而失去穩定的流動態性和成比例公平性[4]。在高速網絡中，由于技術或成本的原因，路由器很可能只有小的緩存[12?14]。另外當與其它基于丟包的擁塞控制算法(如：Reno)共存時，不可避免會因為這些流擠占帶寬而導致丟包。因此，對丟包事件的特殊處理使得FAST TCP在理論上很完美但在實際有背景流的條件下卻不能獲得理想的性能。文獻[11]對此有所改進，但以損失一定的公平性和反應速度為代價。

研究表明，時延和丟包之間的相關性很弱，很難利用時延準確預測丟包[15]。即僅利用排隊時延不能完全避免丟包，一旦丟包，排隊時延就不再增長，這時利用排隊時延作為擁塞度量已不能有效控制發送速率。因此本文提出了一種基于丟包率和排隊時延的擁塞控制模型，采用雙模控制方法，在瓶頸路由器上有足夠緩存時，盡可能發揮用排隊時延作為擁塞度量的優點，盡量避免丟包，使各流獲得穩定的動態性和成比例公平性。而當瓶頸路由器上沒有足夠緩存時，丟包率較大時，模型以丟包率為擁塞度量，使各流仍能獲得與不丟包情況下相近的流特性。該模型在這兩種模式的切換中仍能保持穩定性，實現平滑過渡。

2 基于丟包率和排隊時延的擁塞控制算法

2.1 模型的設計思路

作為擁塞度量，雖然排隊時延比丟包率有更多的優勢，但僅利用排隊時延并不能完全避免丟包。在網絡不發生丟包或者丟包較少時，選擇排隊時延作為擁塞度量能獲得穩定的流動態性，而當丟包較大時，選擇排隊時延已不能正確反應網絡擁塞情況，必須對丟包事件做出反應。因此，需要在這兩種工作模式間尋找一種平滑過渡的方式，兩種情況下算法在平衡點、穩定性和公平性上要盡可能相近，同時在切換過程中仍能保持流的穩定性。

無論是基于丟包率還是基于排隊時延，都不乏高效穩定的成熟模型，可選擇合適的模型使其在新系統的兩種模式下分別發揮作用。但模型的選擇不僅要考慮各自的性能，更重要的是兩種模型結合的可行性。為保證新模型不同工作模式下的平衡點具有統一的公平性，兩種模型的平衡點最好具有相同的公平性，例如同為“max-min”公平或成比例公平。此外，系統還要滿足以下條件：假設模型A的平衡點是[x1, x2,...,xN]，N是流個數，模型B的平衡點是[y1, y2,...,yN]，為保證模型的穩定性，應限制xi/yi=k, i=1, 2,...,N ，k是與i無關的常數。

綜合以上考慮，本文選擇基于時延的FAST TCP模型和修改了的基于丟包率的Kelly模型，兩個模型都具有高效穩定的特點，并且平衡點處吞吐量都符合或近似符合成比例公平。本文模型在文中稱為KFAST。

FAST TCP假定鏈路緩存有能力容納所有流的冗余分組，在平衡時每個流在鏈路緩存保持一定數目的冗余分組。其窗口w調整的遞推公式為

其中加權系數γ∈(0, 1]用來調整窗口變化的平滑程度，αi用來控制冗余分組的參數，N是流個數，qi(t)是流i在第t個調整時刻測量的排隊時延，di是流i的傳播時延(往返)，di+qi(t)為流i的往返時延。

FAST TCP平衡點處發送速率具有x?=α/ii的形式，即平衡時刻流i在路徑緩存中共維護αi個冗余分組，其吞吐量符合αi加權的比例公平。文獻[16]證明了該模型在忽略反饋時延，單瓶頸鏈路條件下的平衡點具有全局漸近穩定性。

Kelly模型[17]是一種經典的基于速率等式的擁塞控制模型，其速率調整的遞推公式為

pi(t)是網絡給出的反饋，θi, ηi分別是調整速率和公平性參數。Kelly模型本身沒有規定反饋的具體形式，可以是丟包信息，也可以是排隊時延。選擇不同的反饋，可以得到具有不同平衡點和公平性的模型。

在單瓶頸鏈路條件下，Kelly模型在平衡點處吞吐量符合ηi加權的成比例公平，多瓶頸鏈路情形下，只要流獲得的網絡反饋等于流途經所有鏈路上的反饋之和，平衡點處吞吐量也符合ηi加權的比例公平。如果流獲得網絡反饋等于途經所有鏈路上的最大反饋，則平衡點處可獲得符合max-min公平的吞吐量，如MKC[18]。以丟包率為反饋，單瓶頸鏈路，各流具有相同反饋時延條件下Kelly模型的全局漸近穩定已由文獻[18]證明。

本文要設計的是基于窗口等式的源算法，為此對Kelly模型做相應修改，并在此后描述本文模型時用t表示第t個時段，而非時刻。修改的Kelly模型中窗口調整的遞推公式為pi(t)和qi(t)分別是流i在時段t結束時刻測得的丟包率和排隊時延，di是流i的傳播時延(往返)，參數βi用于控制平衡時各流的丟包率。與Kelly模型不同，這里的pi(t)是源測得的丟包率，而不是網絡提供的顯式擁塞指示。當丟包率較小時，各流丟包率可以近似等于流途經的各鏈路丟包率之和。因此在丟包率較小時，多鏈路情形下平衡點處各流的吞吐量近似符合βi加權的比例公平。平衡點處的發送速率都具有=β/的形式，除了擁塞度量不同外，i這一點與FAST TCP具有相同的形式。

由上可見，FAST TCP與修改后的Kelly模型在平衡點處發送速率具有相似的形式，吞吐量也近似符合相同的公平性，這些都為它們的有效結合提供了保證。

除了選擇合適的模型外，還要確定兩種工作模式的切換方式。為保證平衡點的全局漸近穩定，在每種參數和網絡條件下都只能有唯一平衡點，同時保證在有限時間之內，系統將不再需要在兩種模式之間切換，并可持續地工作于一種模式之下。實際上，這種兩種工作模式下的控制問題屬于雙模控制問題，其穩定性研究頗具難度。本文選擇了一種實現上較為簡單的切換模式，即優選兩個模型更小的改變量作為新模型的改變量。實驗表明，這種切換方式保證了系統的穩定性。在理論上，本文給出了簡化情形下平衡點的唯一性和穩定性分析。

2.2 模型的數學描述

不考慮反饋時延的情形下，流個數記作為N，流i在時段t內的窗口大小記作為wi(t)，則本文模型為

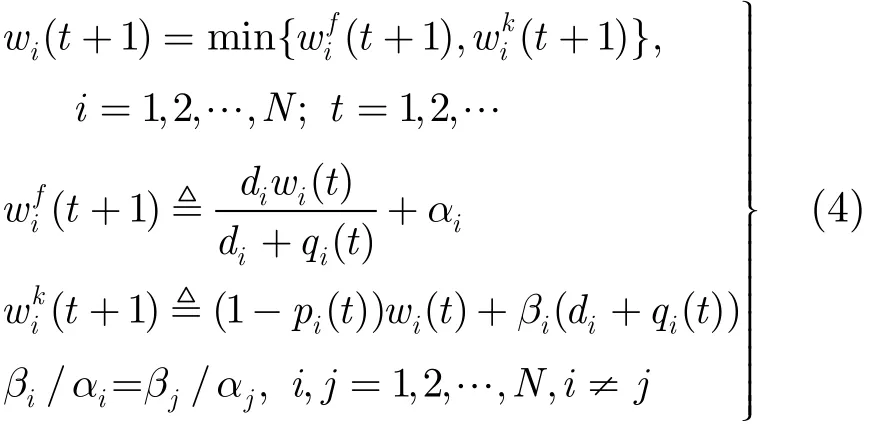
di是流i的傳播時延(往返)，pi(t)和qi(t)分別是流i在時段t結束時刻測得的丟包率和排隊時延，每個流都是一個RTT調整一次。 由于各流的RTT不同，因此它們的調整周期并不相同。

對于單瓶頸鏈路情形，各流共享同一個鏈路，假定鏈路在選擇數據包進行丟棄以及排隊服務策略時對各個流是公平的，那么各流獲得的丟包率和排隊時延都相等。則式(4)中的pi(t)和qi(t)可分別記作為p(t)和q(t)。進一步地，如果單瓶頸鏈路情形下各流具有相同的傳播時延d，則p(t)和q(t)可通過下式計算。

其中L是鏈路的緩存大小，l(t)是時段t結束時刻的隊列長度，C是鏈路帶寬。

對式(5)，式(6)做簡單的解釋，流在時段t的開始時刻根據式(4)調整窗口大小，把窗口里的分組發完之后開始等待，一直到收到第1個分組的ACK以后進入時段t+1。時段t發出的第1個分組的排隊時間是由時段t?1結束時刻鏈路緩存中的隊列長度l(t?1)決定的，那么第1個分組的往返時延就是d+q(t?1)，也就是說時段t持續的時間長度是d+q(t?1)。在此期間內，流向鏈路共發送了個分組，鏈路轉發了C(d+q(t?1))個分組，鏈路的緩存可以存放L?l(t?1)個分組，鏈路共有能力處理C(d+q(t?1))+L?l(t?1)=Cd+L 個分組。如果流發出的分組個數超過了鏈路能處理的分組個數，在時段t的結束時刻，緩存被充滿，并且發生丟包，即得到式(5)。

在不發生丟包的情形下，時段t期間，鏈路本來存放了l(t?1)個包，流向鏈路共發了個包，鏈路轉發了C(d+q(t?1))個包，所以時段t的結束時刻的隊列長度l(t)應該等于l(t?1)+?C(d+q(t?1))=?Cd ，即得到式(6)。

實驗結果表明式(4)定義的系統平衡點具有全局漸近穩定性，然而理論分析只能給出簡化情形下的一些結論。

定理1 設單瓶頸鏈路帶寬為C緩存為L，各流具有相同的傳播時延d。忽略反饋時延，并假設各流享有相同的排隊時延和丟包率，則

由于在FAST TCP模型達到平衡時，流i在鏈路緩存中保留αi個冗余分組[4]。當時，鏈路緩存有能力容納所有流的冗余分組，流可以達到式(7)定義?的?平衡?點。如果L，那么由式(7)定義的w,p, q 將不再是平衡點，丟包不可避免，那么FAST TCP和Kelly模型中哪一個平衡點的丟包率更小，該平衡點就會成為系統的平衡點。

關于平衡點的全局漸近穩定性，本文給出了單瓶頸鏈路單流條件下的結論，如定理2所述。

定理2 設單瓶頸鏈路帶寬為C，緩存大小為L，只有一個流，則

(1)當L≥α，系統的平衡點

是全局漸近穩定的。

(2)當L＜α，

(a)當(α?L)/α≤β/(C +β)，系統的平衡點

是全局漸近穩定的。

(b)當(α?L)/α＞β/(C +β)，系統的平衡點

是全局漸近穩定的。

限于篇幅，定理1和定理2的完整證明在此略去。

3 仿真實驗

3.1 NS-2仿真

本文用NS-2對KFAST進行了仿真，并對KFAST的有效性和性能進行了驗證。

在仿真實現中，用最小RTT來估計傳播時延，與文獻[4]的方法相同。算法的速率控制基本上是基于窗口的。但考慮到突發分組會使大RTT流比小RTT流在鏈路上遭遇更大的排隊時延，導致不公平性，因此在實現中窗口內分組不是連續發送的，而是根據RTT/W計算窗口內分組發送的間隔，定時發送窗口內的分組。為避免不同速率源在瓶頸鏈路獲得不同的丟包率，而導致不公平性，與文獻[2]類似對實際設置的發送間隔時間進行了隨機擾動(以RTT/W為均值的負指數分布)。

仿真實驗的網絡拓撲如圖1所示。分組的大小1000 byte，鏈路緩存管理采用棄尾算法。

3.2 單瓶頸鏈路

實驗1 網絡拓撲如圖1(a)所示。αi=400分組，βi=40分組/s，i=1, 2, 3，瓶頸鏈路緩存L=1000分組，帶寬C=100 Mb/s=12500分組/s。流1從開始時刻一直持續到600 ms，流2在100 ms進入，500 ms離開，流3在200 ms進入，400 ms離開。在200 ms之前，鏈路緩存(L=1000)大于各流冗余分組個數之和(α1+α2=800)，因此鏈路沒有丟包。在流3進入以后，各流冗余分組個數之和變成了α1+α2+α3=1200，大于鏈路緩存，因此出現丟包。一旦流3離開，鏈路又恢復到無丟包的狀態。 各流吞吐量以及丟包率隨時間的變化如圖2所示。其中圖2(b)還顯示了從300 ms到400 ms(系統處于平衡時)的累積丟包率。可以看出，算法在無丟包和有丟包情況下都能獲得穩定、公平的流特性。當流比較少，鏈路緩存足夠大時，算法在盡可能不丟包的前提下使各流獲得盡可能大的帶寬，并公平共享瓶頸帶寬(與各流的RTT無關)。而當流比較多，鏈路緩存不能滿足要求時，算法在維持一定丟包率的前提下，使各流獲得與無丟包情況下相近的性能。

3.3 多瓶頸鏈路

實驗2 如圖1(b)所示，αi=200分組，βi=40分組/s，i=1, 2, 3, 4，3段鏈路b1b2, b2b3, b3b4均有緩存L=500分組，帶寬C=100 Mb/s=12500分組/s，在3段鏈路處分別有α1+α2=400＜L,α1+α3=400＜L,α1+α4=400＜L ，因此每條鏈路上都沒有丟包。

各流的吞吐量變化如圖3所示(各鏈路丟包率均為0)。可見當鏈路緩存足夠大時，模型與FAST TCP的行為相似，獲得穩定的流特性和成比例公平性。

圖1 實驗中的網絡拓撲

圖2 單瓶頸鏈路實驗1的結果

圖3 實驗2的結果

實驗3 如圖1(b)所示，αi=60分組，βi=40分組/s，i=1, 2, 3, 4，3段鏈路b1b2, b2b3, b3b4均有緩存L=60分組，帶寬C=100 Mb/s=12500分組/s。對于流1，假設它在每一段鏈路上的冗余分組都近似相等。那么，在3段鏈路處緩存(L=60)都小于冗余分組之和(60+60/3=80)，系統達到平衡時，3段鏈路上都會有丟包，每個流都會穩定在有丟包的平衡點，考慮到在這種參數條件下，修改的Kelly模型平衡時的丟包率遠小于FAST TCP有丟包條件下的平衡時的丟包率，因此4個流都應該穩定在修改的Kelly模型的平衡點。各流的吞吐量、丟包率及累計丟包率隨時間的變化如圖3所示。

實驗4 如圖1(b)所示，αi=40分組，βi=40分組/s，i=1, 2, 3, 4，3段鏈路b1b2, b2b3, b3b4帶寬均為C=100 Mb/s=12500分組/s，b1b2, b3b4緩存為L1=L3=200分組，b2b3緩存為L2=40分組。顯然，在3段鏈路處分別有α1+α2=80＜L1，α1+α3=80＞L2，α1+α4=80＜L3，在系統達到平衡時，第2段鏈路b2b3會有丟包，則途經該鏈路的流1和流3會丟包。流2和流4沒有丟包，應該穩定在FAST TCP的平衡點。流3丟包，且由于(α1+α3?L2)/(α1+α3)＞(β1+β3)/(C +β1+β3)，由定理1流3應該穩定在修改的Kelly模型的平衡點。流1分別經歷了有丟包和無丟包的鏈路，因此可能穩定在有丟包的平衡點，也可能穩定在無丟包的平衡點，根據調整規則，它會選擇穩定在數值較小的平衡點。考慮到α1=α3，如果流1穩定在有丟包率的平衡點，那么因為流1和流3丟包率相同，因此其平衡點也應該相同，那么流1在鏈路b2b3應該分得近似一半帶寬的吞吐量，因為3段鏈路帶寬相等，流1在其他兩段鏈路上也會分得接近一半帶寬，這顯然將產生矛盾，因此流1只能穩定在FAST的平衡點。由于它經歷3段鏈路，它的時延至少是流2的2倍，所以它能分得的帶寬不會超過鏈路帶寬的1/3。各流的吞吐量、丟包率及累計丟包率隨時間的變化如圖5所示。

在實驗2至實驗4中，雖然參數設置不同，導致丟包情況各不相同，但3個實驗中的吞吐量曲線比較接近。由此可見，在多瓶頸鏈路條件下，無論是無丟包、有丟包，還是部分流有丟包的情況，算法都能獲得相近的公平性和穩定的流特性。

4 結束語

本文提出的基于丟包率和排隊時延的TCP擁塞控制模型采用雙模控制的方法，在瓶頸路由器有足夠緩存時充分發揮排隊時延作為擁塞度量的優點，盡量避免丟包，使各流獲得穩定的動態性和成比例公平性。而當瓶頸路由器沒有足夠緩存，丟包率較大時，模型以丟包率為擁塞度量，使各流仍能獲得與不丟包情況下相近的流特性。該模型在兩種情況的切換中保持穩定的流特性，實現平滑過渡。文獻[19]提出了一種組合排隊時延和顯式擁塞標記作為擁塞度量的FAST TCP改進算法，但該算法需要路由器提供顯式的擁塞指示，而本文算法不需要路由器的顯式支持。

圖4 實驗3的結果

圖5 實驗4的結果

[1] Floyd S. High Speed TCP for large congestion windows.Internet draft draft-floyd-tcp-highspeed-02.txt, work in progress, http://www.icir.org/floyd/hstcp.html, 2003,February.

[2] Gu Y, Towsley D, and Hollot C V, et al.. Congestion control for small buffer high speed networks. Proceedings of IEEE INFOCOM 2007, New York, May 2007: 1037-1045.

[3] Ha S, Rhee I, and Xu L. CUBIC: a new TCP-friendly high-speed TCP variant. ACM SIGOPS Operating Systems Review, 2008, 42(5): 64-74.

[4] Wei D X, Jin C, and Low S H, et al.. FAST TCP: Motivation,architecture, algorithms, performance. IEEE/ACM Transactions on Networking, 2006, 14(6): 1246-1259.

[5] Mo J and Walrand J. Fair end-to-end window-based congestion control. IEEE/ACM Transactions on Networking,2000, 8(5): 556-567.

[6] Xu L S, Harfoush K, and Rhee I. Binary increase congestion control for FAST long distance networks. Proceedings of IEEE INFOCOM 2004, Hong Kong, March 2004: 796-805.

[7] Chen M Y, Zhang J S, and Murthi M N, et al.. Delay-based TCP congestion avoidance: A network calculus interpretation and performance improvements. Computer Networks, 2009,53(9): 1319-1340.

[8] Belhaj S and Tagina M. VFAST TCP: An improvement of FAST TCP. Proceedings of the Tenth International Conference on Computer Modeling and Simulation, IEEE Computer Society, Los Alamitos, CA, USA, 2008: 88-93.

[9] Zhang H, Peng L, and Fan B, et al.. Stability of FAST TCP in single-link multi-source network. Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, IEEE Computer Society, Los Angeles,California, USA, 2009: 369-373.

[10] Zhou J, Zhao F, and Luo Z. Parameter tuning of FAST TCP based on Lyapunov function. Proceedings of the 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, IEEE Computer Society, Wuhan,China, 2008: 738-742.

[11] Yuan C, Tan L S, and Lachlan L H, et al.. A generalized FAST TCP scheme. Computer Communications, 2008, 31(14):3242-3249.

[12] Appenzeller G, Keslassy I, and McKeown N. Sizing router buffers. Proceedings of ACM SIGCOMM 2004, Portland,Aug. 2004: 281-292.

[13] Goringsky S, Kantawala A, and Turner J S. Link buffer sizing:A new look at the old problem. IEEE Symposium on Computers and Communications (ISCC 2005), Murcia,Cartagena, Spain, June 2005: 507-514.

[14] Enachescu M, Ganjali Y, and Goel A, et al.. Part III: routers with very small buffers. ACM SIGCOMM Computer Communication Review, 2005, 35(3): 83-59.

[15] Martin J, Nilsson A, and Rhee I. Delay-based congestion avoidance for TCP. IEEE/ACM Transactions on Networking,2003, 11(3): 356-369.

[16] Wang J, Wei D X, and Low S H. Modeling and stability of FAST tcp. Proceedings of IEEE INFOCOM 2005, Miami, FL,March 2005: 938-948.

[17] Kelly F P, Maulloo A K, and Tan D K H. Rate control for communication networks: Shadow prices, proportional fairness and stability. Journal of Operations Research Society,1998, 49(3): 237-252.

[18] Zhang Y, Kang S, and Loguinov D. Delay-independent stability and performance of distributed congestion control.IEEE/ACM Transactions on Networking, 2007, 15(5):838-851.

[19] Chen M Y, Fan X Z, and Murthi M N, et al.. Normalized queueing delay: congestion control jointly utilizing delay and marking. IEEE/ACM Transactions on Networking, 2009,17(2): 618-631.