無線傳感器網絡分布式一致時間同步協議的收斂分析及加速設計

李 立 劉勇攀 楊華中 汪 蕙

(清華大學電子工程系清華信息國家實驗室 北京 100084)

1 引言

時間同步協議是傳感器網絡的研究熱點之一。早期的全網時間同步協議多是集中式的，如傳感器網絡時間同步協議[1](Timing-sync Protocol for Sensor Networks，TPSN)等。它們由根節點發起同步，通過建立全網路由來傳播同步消息。接收到同步消息的節點根據消息中攜帶的時間信息調整本地時間，最終使全網節點都與根節點的時間同步。集中式時間同步協議存在以下幾個缺點。(1)可擴展性差。新加入的節點需要等待路由建立后才能開始同步。(2)抗毀性差。一旦同步路由出現中繼節點失效的情況，部分節點將由于接收不到同步消息而失去同步。(3)同步誤差會沿同步路由累積[2]。距離根節點的跳數越多，誤差越大。(4)同步路由的建立和周期性維護會消耗大量的能量和帶寬資源。

近年來出現了分布式的時間同步協議[3?8]，它們不需要建立全網路由來分發同步消息，從而避免了集中式協議的上述缺點。在文獻[3]提出的同步協議中，節點估計自己與根節點的時間相位差，并利用分布式融合使全網節點與根節點保持時間同步。由于文獻[3]中的同步協議依賴于根節點提供網絡參考時間，它在抗毀性方面存在問題。一旦根節點失效，需要重新選出根節點并與之建立同步。基于分布式一致的全網時間同步(Distributed Consensus Time Synchronization, DCTS)協議[4?8]通過鄰居節點間的信息融合，使全網節點的時間都同步到一個虛擬的時間，避免了根節點失效所帶來的全網重新同步的問題。由于DCTS依賴于擴散來傳遞同步信息，導致其收斂速度慢于集中式同步協議，這是制約其在網絡中廣泛使用的一個瓶頸。現有提高DCTS收斂速度的方法主要是構造二階迭代矩陣[6]，這種方法的缺點在于需要計算全網鄰接矩陣的特征值來確定迭代矩陣的參數，而大規模網絡的鄰接關系通常難以獲得。此外，傳感器節點的處理器也沒有計算大規模矩陣特征值的能力。

本文通過將DCTS的迭代過程映射到馬爾可夫鏈的狀態轉移過程來分析其收斂特性，推導出DCTS在循環網中的收斂速度決定于網絡規模與節點鄰居數的比值，并通過仿真實驗證實該結論對于節點近似均勻分布的規則網絡(類均勻規則網)和節點近似均勻分布的非規則網絡(類均勻網)也成立。此外，DCTS在類均勻網的收斂速度還受到節點鄰居數分布的影響。基于此，本文提出通過調整網絡鄰居數分布來加速DCTS的分布式算法。仿真結果表明該算法能有效提高DCTS在類均勻網中的收斂速度。

本文結構安排如下：第2節介紹DCTS的數學模型；第3節基于馬爾可夫鏈分析DCTS的收斂特性；第4節提出基于鄰居數分布調整的DCTS加速算法；第5節通過仿真對加速算法的效果加以驗證；最后給出了全文的總結。

2 DCTS的數學模型

節點vi的本地時間ci(t)可用一階線性方程ci(t)=fi?t+pi表示，其中fi和pi分別是vi的晶振頻率以及初始相位，t是真實世界時間。由于不同節點的頻率存在細微差別(典型值為1～100 ppm)，所以即使所有節點同時開機，它們的本地時間也會隨著時間推移出現偏差，這就是需要時間同步協議的原因。

DCTS包括本地估計、交換和更新同步信息3個步驟。這里的同步信息，可以是節點的本地時間[4]，也可以是節點估計的虛擬參考時間的頻率和相位[5]，但無論交換何種同步信息，其一致性操作都是一樣的。由于本文的重點在于分析和加速一致性同步的收斂，所以不區分這些同步信息，統一把它們視為節點的時間信息ti。

DCTS的執行過程可以描述為：每個節點通過與鄰居節點交換時間信息，把自己下一時刻的時間信息更新為自己及鄰居節點當前時間信息的加權和。于是，節點vi本地時間信息的迭代更新過程可以用數學模型式(1)來表示，其中m為迭代次數，Ni為vi的鄰居節點集合，wij表示vi更新時間信息時節點vj對應的權重。

一個網絡可以用圖的方式表示為N(V,E)，其中V={v1,v2,…,vn}表示節點集合，E對應于節點間的單跳通信鏈路集合E={(i,j)}。假設網絡是強連通的，節點間的通信雙向可達。令t(m)=(,,…,)為網絡節點在m時刻的時間信息向量，W為一階更新迭代矩陣，DCTS的迭代過程可用矩陣形式(2)來表示

3 基于馬爾可夫鏈的DCTS的收斂特性分析

文獻[3]曾將算法的迭代過程映射到馬爾可夫域，導出了算法收斂速度與網絡邊連通度、根節點鄰居數和網絡規模等參數的關系。由于網絡邊連通度需要知道全網鄰接關系才能獲得，且難以通過節點的本地調整加以改變，所以文獻[3]中的結論無法用于設計分布式的DCTS加速算法。本文采用馬爾可夫鏈的相關理論來分析DCTS算法的收斂特性與其他網絡參數間的關系。

3.1 DCTS的收斂性

首先把DCTS的迭代過程映射為馬爾可夫鏈的狀態轉移過程。映射關系如式(3)，其中網絡中的節點對應于馬爾可夫鏈的各個狀態S={s1,s2,…,sn}，為區別于迭代矩陣W，用P表示馬爾可夫鏈的轉移概率矩陣。

在強連通且節點數有限的網絡中，DCTS迭代映射得到的馬爾可夫鏈MN是有限不可約遍歷鏈。根據馬爾可夫鏈的相關理論可知，存在正整數k，使Pk＞0，且limm→→Pm=1πT，其中π是馬爾可夫鏈MN的唯一穩態分布，是滿足1Tπ=1的正列向量。由式(4)可知，隨著迭代次數增加，各節點的時間信息將趨于一致，即達到同步。

文獻[4]在設計迭代矩陣W時，要求wij=wji。此時W是雙隨機的，馬爾可夫鏈有均勻穩態分布π=(1/n,1/n,…,1/n)T，各節點最終收斂到初始時間信息的平均值11Tt(0)/n。文獻[7]中的迭代矩陣定義如式(5)所示，其中di表示節點vi的度，即鄰居節點數。下面的分析都基于迭代矩陣式(5)進行。

在非規則網絡中，節點的鄰居數各不相同，迭代矩陣式(5)不滿足雙隨機條件，節點收斂到它們初始時間信息的加權平均值為

3.2 DCTS收斂速度的分析

DCTS中節點的時間信息達到同步等效于其映射的馬爾可夫鏈MN收斂到穩態。由于MN遍歷，且時間可逆(對于MN的任意兩個狀態sisj，有πipij=πipji)，MN的轉移概率矩陣P的特征值滿足1=λ1＞λ2,…,λn＞?1。MN的收斂速度取決于矩陣P的模第二大特征值λ*=max(λ2,|λn|)，其收斂所使用的迭代次數為m=1/logk(1/λ*)[9]。

時間可逆的馬爾可夫鏈，其轉移概率矩陣的模第二大特征值滿足Cheeger’s不等式[10]，即1-2Φ≤λ≤1?Φ2/2，其中Φ稱為馬爾可夫鏈的導通系數，可用式(7)計算。S*是馬爾可夫鏈所有狀態的一個子集，其穩態分布之和滿足πi∈(0,1/2]。

循環網中DCTS收斂速度的界 首先分析DCTS在圖1所示的循環網C中的收斂速度。循環網是規則的，每個節點有相同鄰居數，設為d。根據式(5)可知在循環網中，DCTS的迭代矩陣W的所有非零元素都等于1/(d+1)，且映射得到的馬爾可夫鏈MC有均勻穩態分布。于是，式(7)可簡化為式(8)，其中|C(S*,)|表示連接節點子集合S*和其補集S*的割邊數，|S*|表示集合S*所包含的節點個數。

循環網的最小割邊數與所選擇的節點子集S*的

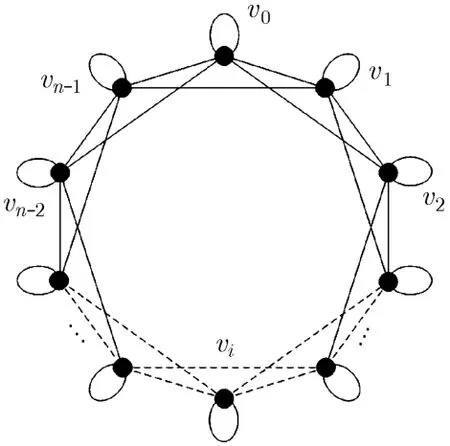
圖1 循環網C

大小有關，可具體表示為式(9)，其中S+表示給定集合大小為|S+|時所選擇的有最小割邊數的節點子集。

當網絡規模較大時，d/n和d2/8n2趨近于0，λ*趨近于1，收斂速度m≈1/(1-λ*)[9]。DCTS在循環網中的收斂速度可近似表示為式(11)，說明DCTS在循環網中的收斂速度與網絡規模與節點鄰居數的比例n/d相關。

3.3 類均勻網中DCTS的收斂速度分析

3.2 節得到了循環網中DCTS收斂速度與網絡規模和鄰居數的關系。由于實際的傳感器網絡不會是循環網，所以需要分析DCTS在更一般的網絡結構中的收斂速度。

3.3.1 類均勻網的定義 傳感器網絡可以采用在監測區域里均勻布置節點的方式構成。假設監測區域為矩形。把整個監測區域劃分為若干個等面積的小矩形，在每個小矩形的頂點布置一個傳感器節點，得到如圖2中虛線所示的格子形網絡。由于布置時的偏差或是受到外力的影響，實際網絡的節點不會如格子形網絡中那樣整齊排列。給圖2中每個節點的位置隨機加上一個正的偏移向量(向量的模小于格子形網絡中相鄰節點距離的一半)，得到如圖2中實線所示的“類均勻網”。這里的“類均勻”是指監測區域單位面積內的節點個數基本相等。

圖2 均勻網絡和類均勻網絡

當節點的傳輸半徑一定時，位于網絡邊緣的節點的鄰居數少于位于網絡中心的節點，類均勻網是非規則的。假設通過調整傳輸半徑，使網絡中的每個節點都有相同的鄰居數，可以得到類均勻“規則”網。如果類均勻“規則”網中所有的節點都有d個鄰居，它稱為d-規則的。類均勻網和類均勻規則網比循環網具有更一般的傳感器網絡形態。

3.3.2 類均勻網中DCTS的收斂速度 首先測試DCTS在類均勻d-規則網中的收斂速度。比較下面兩種情形：(1)鄰居數d不變，網絡規模n增加；(2)網絡規模和鄰居數同比例增加，即保持n/d不變。圖3(a)標出了DCTS使節點時間的相對誤差小于10?6所需要的迭代次數的比較。仿真結果表明式(11)中的結論在類均勻規則網中也成立。隨著網絡規模的增加，僅保持鄰居數d不變會導致DCTS的收斂迭代次數近似線性地增加；而保持n/d不變可以使收斂速度維持在一個相對穩定的值。

隨后本文在4個規模為100的類均勻網中測試了DCTS的收斂速度。測試結果如圖3(b)和圖3 (c)所示，其中也同時標出了每個網絡中鄰居數分布的均值和標準差。可以看到，由于類均勻網中節點的鄰居數不同，鄰居數分布的均值和方差會共同影響DCTS的收斂速度。當鄰居數分布標準差較小、網絡近似于規則時，節點鄰居數的均值決定DCTS的收斂速度(圖3 (b))。反之，當節點鄰居數相差較大時，鄰居數分布的方差也會影響DCTS的收斂速度(圖3 (c))。

4 DCTS加速算法

第3節的分析和實驗結果表明，節點的鄰居數分布會影響DCTS在類均勻網中的收斂速度。由于傳感器節點可以動態地調整其無線收發機的發射半徑來增加或減少鄰居節點，所以可以通過改變節點的鄰居數分布來加速DCTS收斂。

4.1 算法描述

加速算法包括初始化和分布式鄰居數調整兩部分。初始化部分負責為每個節點構造本地鄰居表。其執行過程描述如下：(1)節點vi設置發射半徑為最低等級，發送“請求鄰居消息”，其中包括發送節點ID和當前發射半徑等級；(2)節點vj如果是首次接收到來自vi的“請求鄰居消息”，則按照“請求鄰居消息”中的發射半徑等級調整發射功率，回復“請求鄰居應答消息”，報告自己的ID；(3)當節點vi接收到vj回復給自己的“請求鄰居應答消息”，在鄰居表中記錄下該節點的ID，及與其通信所需要的發射半徑；(4)節點vi提高發射半徑，重復步驟(1)-步驟(4)直至發射半徑等級到達最大。初始化完成后，本地鄰居表中的鄰居節點按照其與vi通信所需的發射半徑等級升序排列。由于隨著節點發射半徑的調整，鄰居數也會相應改變，用“當前鄰居數”表示節點vi在當前發射半徑下的鄰居數。

圖3 收斂速度比較

分布式鄰居數調整部分的目標是減小節點間鄰居數的差異和增加網絡的平均鄰居數。前者是為了減少節點鄰居數的差異對收斂速度的不利影響。算法1描述了一種分布式調整算法，可以在保持網絡平均鄰居數不變的情況下，減小網絡中節點鄰居數的差異。

算法1 DCTS的分布式鄰居數調整算法1(DCTS-ACC1)

(1)所有節點設置周期性同步定時器和初始發射半徑R；

(2)當節點vi的同步定時器被觸發時，廣播“同步請求消息”，設置同步應答定時器；

(3)接收到“同步請求信息”的節點vj回復“同步應答消息”，報告節點ID，時間信息tj和當前鄰居數dj；

(4)節點vi接收“同步應答消息”，保存其中的ID信息，時間信息和鄰居數信息。當同步應答定時器被觸發時，

(a)基于式(1)調整本地時間信息ti；

(b)比較鄰居節點的當前鄰居數，找到最大和最小值dmax和dmin。若|dmax-dmin|≥Δ，執行步驟(c)；否則不做鄰居數調整；

(c)發送“鄰居調整消息”給當前鄰居數最大/最小的節點vmax/vmin，通知其減少/增加一個鄰居節點。

(5)接收到“鄰居調整消息”后，節點vmax/vmin查詢鄰居表，調整發射半徑以減少/增加一個鄰居節點。

算法1通過不斷減小/增加鄰居節點中的最大/最小鄰居數，使不同節點的鄰居數越來越接近，從而減小全網節點的鄰居數差異。由于鄰居數必須是整數，所以算法1不能保證各個節點的鄰居數收斂到同一個值(這取決于網絡調整前總的鄰居數)。當本地鄰居數之差小于給定閾值Δ時，就停止鄰居數的調整。在算法1中，由于當某節點增加鄰居時必有另一節點同時減少相等數目的鄰居，所以網絡總的鄰居數和平均鄰居數保持不變。

當鄰居數分布的方差減小后，網絡鄰居數均值將決定DCTS的收斂速度。從加速算法收斂的角度出發，需要提高網絡鄰居數均值。算法2把節點的鄰居數都增加到本地鄰居數的最大值。通過迭代，節點的鄰居數都收斂到網絡調整前的最大鄰居數。

算法2 DCTS的分布式鄰居數調整算法2(DCTS-ACC2)

(1)所有節點設置周期性同步定時器和初始發射半徑R；

(2)當節點vi的同步定時器被觸發時，廣播“同步請求消息”，設置同步應答定時器；

(3)接收到“同步請求信息”的節點vj回復“同步應答消息”，報告本地節點ID，時間信息tj和當前鄰居數dj；

(4)節點vi接收“同步應答消息”，保存其中的ID信息，時間信息和鄰居數信息。當同步應答定時器被觸發時，

(a)基于式(1)調整本地時間信息ti；

(b)比較鄰居節點的當前鄰居數，找到最大值dmax。若當前鄰居數di≠dmax，執行步驟(c)；否則不做鄰居數調整；

(c)查詢鄰居表，調整發射半徑使鄰居數達到dmax。

算法1僅減小了節點鄰居數差異對DCTS收斂速度的影響，而算法2在消除了節點鄰居數差異的同時還增加了鄰居數均值，所以會有更好的加速效果。但是，算法1在增加部分節點發射半徑的同時減小了另一部分節點的發射半徑，而算法2則提高了網絡中大部分節點的鄰居數和發射半徑，所以對網絡平均發射半徑和能耗的影響會大于算法1。

4.2 有效加速鄰居比

由于鄰居數調整算法的加速效果和網絡平均發射半徑及能耗互為制約，那么對于規模一定的類均勻規則網而言，是否存在較優的鄰居數，能在有效加速DCTS收斂的同時也不過多地增加網絡平均發射半徑和能耗。

當循環網的規模一定時，由式(11)可知DCTS的收斂速度與鄰居數成反比。也就是說，當鄰居數較小時，增加它可以顯著減少DCTS的收斂迭代次數；而隨著鄰居數的增加，迭代次數的減少速度開始變慢，此時再持續增加鄰居數的加速效果不明顯。

用加速閾值vthd表示當鄰居數增加1時，DCTS所減少的收斂迭代次數。定義“有效加速鄰居比”如下。

定義1 在規則網絡中，有效加速鄰居比feff為滿足加速閾值vthd的最小鄰居數和網絡規模的比值。

令式(11)中迭代次數的下限為f(d)，其關于鄰居數d的一階導數的絕對值為|f'(d)|=n/ d2。|f'(d)|反映了隨著鄰居數變化，循環網中DCTS收斂迭代次數下界的變化速度。當減少量開始少于閾值vthd時，當前的鄰居數與網絡規模的比就是有效加速鄰居比的下界。同理可以得到有效加速鄰居比的上界，如式(12)所示。

表1列出了當vthd為1和10時，不同規模循環網中有效加速鄰居比的上下界和均值。當給定閾值時，隨著網絡規模增加，有效加速鄰居比的上下界以及均值都呈下降趨勢，且下降速度逐漸變慢。

表1 vthd=1,10時的有效加速鄰居比的上、下界及均值

5 實驗結果

為了驗證本文提出的加速算法的加速效果，基于Matlab平臺進行了網絡仿真實驗。相關參數設置如下：監測區域面積為100×100 m2，傳感器節點構成類均勻網，網絡規模為36-400，節點的初始傳輸半徑為20 m。

5.1 DCTS加速算法在類均勻網中的加速效果對比

圖4對比了當類均勻網的規模為100個節點時，初始和經過加速算法調整的DCTS的收斂速度。表2列出了加速調整前后網絡鄰居數分布的均值、標準差以及節點平均傳輸半徑。其中，DCTS-ACC1算法的迭代次數約為調整前的75%，DCTS-ACC2的迭代次數約為調整前的50%。表2則表明，采用DCTS-ACC1算法時，網絡的平均傳輸半徑與調整前相當，而DCTS-ACC2由于增加了網絡中大部分節點的傳輸半徑，使全網平均發射半徑比調整前增加了約24%。

圖4 收斂速度對比

表2 加速調整前后的鄰居數分布和平均傳輸半徑

5.2 類均勻規則網的有效加速鄰居比

圖5(a)標出了在網絡規模為400個節點的類均勻d-規則網中，對應于不同鄰居數d，DCTS的收斂迭代次數。可以看出在網絡規模固定時，隨著鄰居數d增加，收斂迭代次數的減少量呈先大后小的趨勢，這與循環網的情況(式(11))一致。圖5(b)標出了當速度閾值vthd分別取1和10時，不同規模類均勻規則網的有效加速鄰居比。在兩種閾值下的有效加速鄰居比隨網絡規模變化的趨勢都與循環網類似，即隨著網絡規模增加，有效加速鄰居比逐漸減小并趨于穩定，大規模網絡的有效加速鄰居比趨于常數。

圖5 有效加速鄰居比

6 結束語

本文通過將DCTS迭代過程映射到馬爾可夫鏈的狀態轉移過程，研究其收斂和加速問題。從分析和仿真結果可以看出，DCTS在循環網和類均勻規則網中的收斂速度與網絡規模與鄰居數的比值有關；而在類均勻網中，節點的鄰居數分布也會影響DCTS的收斂速度。因此本文提出了通過調整節點鄰居數分布來加速DCTS收斂的分布式算法。仿真結果表明該算法可以有效提高DCTS的收斂速度，在100個節點的類均勻網中，算法DCTS-ACC1在沒有增加節點平均傳輸半徑的情況下將DCTS收斂迭代次數減少了約25%。此外，為避免過度增加鄰居數而消耗較多的傳輸能量，引入了“有效加速鄰居比”以確定類均勻規則網的較優加速鄰居數，并利用給定的速度閾值和網絡規模推導出循環網有效加速鄰居比的上下界。仿真結果表明，類均勻規則網的有效加速鄰居比隨網絡規模的增加逐漸減小并趨于穩定，變化趨勢類似于循環網。

[1] Ganeriwal S, Kumar R, and Srivastava M B. Timing-sync protocol for sensor networks. Proceedings of the First International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 2003: 138-149.

[2] Sommer P and Wattenhofer R. Symmetric clock synchronization in sensor networks. ACM Workshop on Real-World Wireless Sensor Networks, Glasgow, Scotland,2008: 11-15.

[3] Giridhar A and Kumar P R. Distributed clock synchronization over wireless networks: algorithms and analysis. Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, USA, 2006: 4915-4920.

[4] Li Q, Rus D. Global clock synchronization in sensor networks.IEEE Transactions on Computers, 2006, 55(2): 214-226.

[5] Schenato L and Gamba G. A distributed consensus protocol for clock synchronization in wireless sensor network. 46th IEEE Conference on Decision and Control, New Orleans, LA,USA, 2007: 2289-2294.

[6] Gang X and Kishore S. Second order distributed consensus time synchronization algorithm for wireless sensor networks.Global Telecommunications Conference, IEEE, New Orleans,LA, USA, 2008: 1-5.

[7] Sommer P and Wattenhofer R. Gradient clock synchronization in wireless sensor networks. International Conference on Information Processing in Sensor Networks,San Francisco, USA, 2009: 37-48.

[8] Gang X and Kishore S. Performance of distributed consensus time synchronization with gaussian delay in wireless sensor networks. Wireless Communications and Networking Conference, IEEE, Budapest, Hungary, 2009: 1-5.

[9] Boyd S, Diaconis P, and Xiao L. Fastest mixing Markov chain on a graph. Siam Review, 2004, 46(4): 667-690.

[10] Kannan R. Markov chains and polynomial time algorithms.35th Annual Symposium on Foundations of Computer Science, Santa Fe, New Mexico, USA, 1994: 656-671.