超磁致伸縮驅動器二維軸對稱非線性驅動位移模型及有限元分析*

譚先濤，楊斌堂，孟 光，徐彭有，楊德華

(1. 上海交通大學機械系統與振動國家重點實驗室，上海 200240；2.中國科學院國家天文臺南京天文光學技術研究所，南京 210042)

由于大口徑鏡面制造困難，目前世界上的大口徑天文光學望遠鏡方案均采用了拼接子鏡主動光學技術，采用六面體或者扇形子鏡拼接而成，并通過單個鏡面的精密控制來實現整體鏡面的協調一致。控制單個鏡面的微位移驅動器需要具有高精度、大行程以及大負載的技術要求。目前廣泛使用的微位移驅動包括電機驅動、液壓驅動、壓電驅動等驅動方式。電機驅動的機械式微位移驅動器存在著間隙、傳動誤差、摩擦損耗及爬行等現象，難以到達高精度的要求；液壓驅動的微位移驅動器分辨率較低、輸出負載能力較小、反應速度較慢；壓電驅動器具有高分辨率大承載等優點，但由于壓電應變量較小，難以實現大行程，并且需要高電壓驅動，發熱嚴重。超磁致伸縮驅動器(Giant Magnetostrictive Actuator，GMA)具有輸出位移和輸出力大、機械響應速度快等優點，在大型天文望遠鏡拼接子鏡的精密驅動控制方面具有潛在優勢。

GMA的核心部件為超磁致伸縮材料(Terfenol-D)棒。Terfenol-D作為一種稀土超磁致伸縮材料，具有非常復雜的電磁-結構-熱多物理場耦合特性，并且其材料屬性如相對磁導率、彈性模量等隨外加磁場、預壓應力以及溫度的變化而變化。建立精確的數學模型，并選用有限元計算方法對GMA進行仿真分析，從而優化GMA的結構和電磁性能，對提高GMA的輸出性能具有重要意義。

針對GMA的研究，Engdahl、Perez和Kannan[1-3]分別建立了描述其耦合特性的模型，但是都沒有考慮到材料屬性參數的非線性變化；Benatar[4]采用FEMLAB計算了耦合三維有限元模型，但也沒有考慮參數的非線性；趙章榮[5]引入Jiles-Atherton磁滯模型建立了三維動態有限元模型，但由于模型的強非線性，三維模型計算復雜，不易得到收斂結果。基于以上分析，并結合所設計驅動器實際工作環境，本研究采用Jiles-Atherton模型計算磁化強度M、磁致伸縮量λ和磁場強度H、預壓應力σ0之間的非線性關系，建立了二維軸對稱非線性有限元模型，并嘗試使用商用有限元軟件COMSOL 3.5實現了整個驅動器的電磁-結構全耦合分析。

1 超磁致伸縮驅動器二維軸對稱非線性位移模型

直動型超磁致伸縮驅動器的工作原理是由勵磁線圈通入電流產生電磁場，超磁致伸縮棒(Terfenol-D)在磁場作用下，由于內部磁疇的偏轉而產生伸縮變化，并由輸出頂桿輸出位移和力，驅動負載。

基于驅動器的軸對稱性質，采用二維軸對稱方式建立驅動器建立有限元模型，不僅可以保證求解的精度不下降，同時可以大大節省計算機資源。如圖1，為超磁致伸縮驅動器的結構模型。

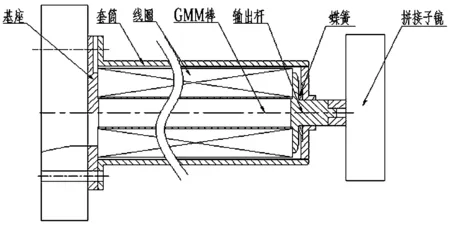
圖1 GMA結構示意圖Fig.1 Structure of a giant magnetostrictive actuator(GMA)

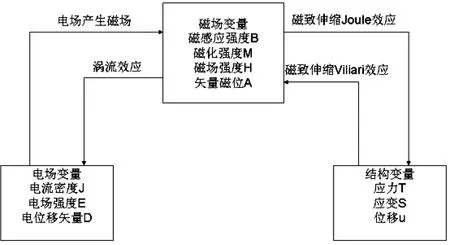
圖2 超磁致伸縮驅動器電磁場和機械應力場耦合關系Fig.2 Illustration of the couplings between electromagnetic field and mechanical stress field in a GMA

如圖2，驅動器中包含電磁—機械的雙向耦合。利用有限元方法分析超磁致伸縮驅動器的性能，實際上就是求解描述耦合物理場偏微分方程邊值問題。以下過程將首先建立電磁場和機械應力場的偏微分方程及其邊界條件，然后引入Jiles-Atherton模型描述Terfenol-D棒內的電磁—機械耦合特性。

1.1 超磁致伸縮驅動器的電磁場

驅動器工作在電磁場中，采用Maxwell方程組描述電磁場特性[6]：

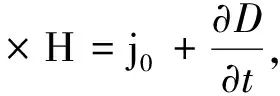
(1)

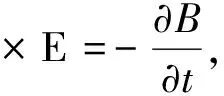
(2)

▽·D=ρ,

(3)

▽·B=0,

(4)

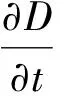
針對驅動器的軸對稱特性，使用磁矢量勢描述電磁場，則只有圓周方向分量Aφ≠0。

根據(1)可知：

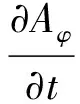
(5)

對上式兩邊同時乘以δAφ(δAφ表示Aφ的變分)，并在整個域內積分，可得積分弱解形式方程為：

▽×δAφ)tHdΩ+

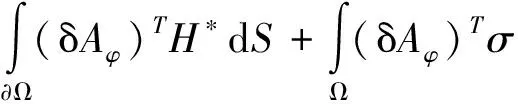
(6)

電磁場方程求解的初始和邊界條件為：

A|t=0=A0， ?ΩA∶A=A*

A|t=0=V0， ?ΩV∶V=V*

(7)

1.2 超磁致伸縮驅動器的機械應力場

根據牛頓第二定律，Terfenol-D棒內部力平衡方程為：

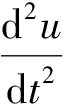
(8)

其中T為應力；b為體積力；u=[u,w]T；u、w分別表示徑向和軸向的位移。

應力-應變關系根據胡克定律有：

T=CS

(9)

其中C為剛度矩陣；S為應變向量。應變-位移關系為：

(10)

對式(8)兩端同時乘以δu，并在整個域內積分，可得積分弱解形式方程：

(11)

應力張量T由3部分組成[2]：機械應力分量Tmech；Maxwell應力張量Tm；預壓應力張量T0。其中：

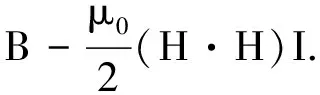
(12)

機械應力場方程求解的初始和邊界條件為：

(13)

1.3 GMM內的磁-結構耦合場

GMM中磁場H由線圈的源磁場Hs以及磁化產生的磁場HM組成[7]：

H=Hs+HM

(14)

式中HM=-▽φ,φ表示簡化磁標量位，則GMM中的磁場強度可表示為：

H=-▽φ+Hs

(15)

A E Clark在1980年提出了描述超磁致伸縮效應的線性壓磁方程：

S=T/YH+dH,

(16)

B=dT+μTH.

(17)

其中YH、d和μT分別表示Terfenol-D棒的彈性模量矩陣、壓磁系數矩陣和磁導率矩陣；上標H,T分別表示恒定磁場和恒定應力條件。

線性壓磁方程是在一定的外加偏置磁場和預壓力作用下，忽略磁滯非線性特性的基礎上得到的，能夠描述磁致伸縮和逆磁致伸縮效應，但不能反映材料的磁滯回特性。

Jiles和Atherton建立了J-A磁滯模型[8-9]，該模型基于微磁學理論和Weiss磁籌理論，表達式簡單，參數較少。本文采用J-A模型描述Terfenol-D棒的磁化過程。包含外加可變預應力σ0的J-A模型表達式為：

(18)

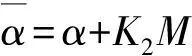
表1 預壓應力為8MPa，最大電流為8A時通過遺傳算法辨識出的J-A模型參數

壓磁方程中，總的應變是由彈性應變T/YH和磁致伸縮應變dH兩部分構成。磁致伸縮應變λ=dH根據二次疇轉模型可寫為：

(19)

式中M可以通過J-A模型，采用四階Runge-Kutta法計算求得。計算得到的M-H,λ-H，曲線如圖3。

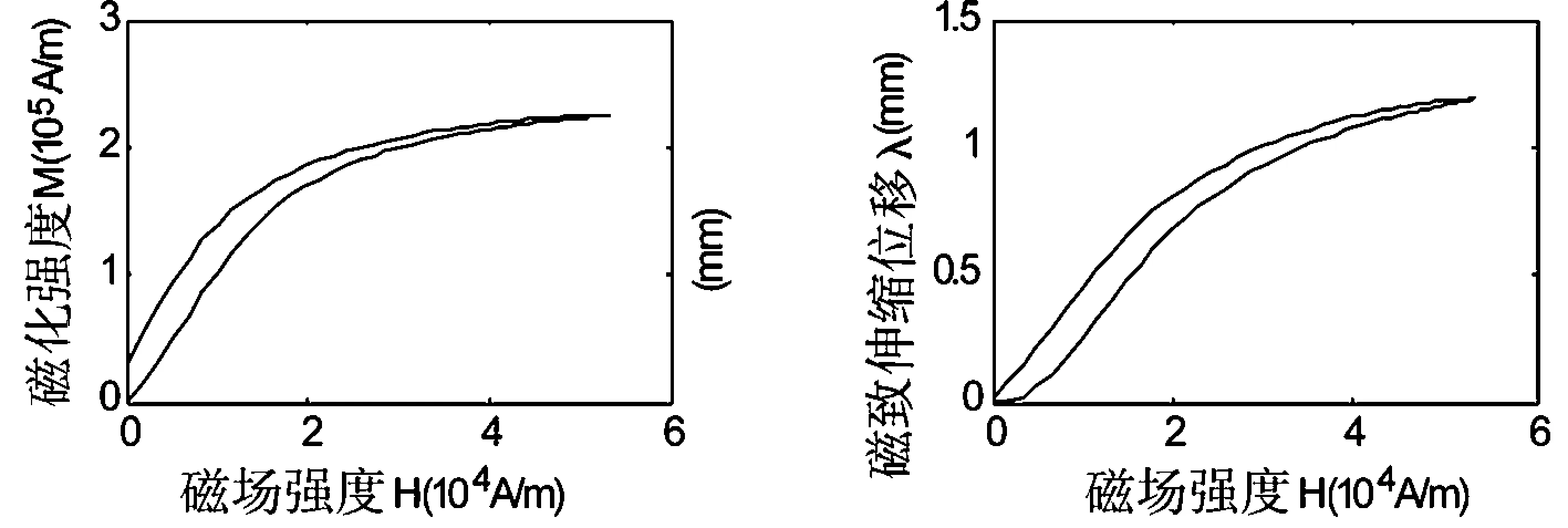
圖3 根據Jiles-Atherton磁滯模型計算得到的磁化強度、磁致伸縮量和磁場強度的函數關系Fig.3 The variations of magnetization and magnetostriction displacement with magnetic field intensity according to the Jiles-Atherton model

將上述獲得的M-H、λ-H關系寫成代數插值表達式，帶入(16)中可以得:

T=EHS-EHλ

(20)

磁致伸縮棒內的磁感應強度B可以通過B、H、M之間的關系獲得：

B=μ0(M+H)

(21)

(20)、(21)即為包含磁滯的非線性本構關系。

根據以上分析，(6)、(11)分別為電磁場和機械應力場的控制方程；(7)、(13)分別為兩個物理場的邊界條件。同時考慮(20)、(21)的本構方程式，采用有限元方法進行求解。

2 COMSOL Multiphysics 3.5求解及實驗結果比較

COMSOL Multiphysics是一款大型的高級數值仿真軟件。它基于偏微分方程組定義物理模型，具有很好的交互開發環境界面。COMSOL Multiphysics成功實現了任意多物理場、直接、雙向實時耦合。既可以直接選擇封裝的模塊來模擬某一類型的物理模型，也可以采用PDE(Partial Differential Equations)模塊來直接定義特殊的物理模型。基于超磁致伸縮材料獨特的磁-結構非線性耦合特性，在比較了常用的數值仿真軟件如ANSYS之后，最終選用了COMSOL Multiphysics 3.5作為解決超磁致伸縮材料非線性多物理場耦合問題的計算分析平臺。

在COMSOL Multiphysics3.5中，首先選擇模型的空間維度為2D軸對稱，然后設置3個物理環境：2D軸對稱應力-應變模型，變量{uor,w,p};2D軸對稱磁場模型，變量{Aphi}；2D弱解模型，變量{u1,w1,Vm}。輸入幾何模型之后，即可以設置參數、表達式、函數來定義物理環境常量及變量(材料參數、求解域參數、邊界設定等)。對于應力-應變模型和磁場模型，可以直接設置這些參數，而對于弱解模型，自定義的弱解表達式如表2。

表2 自定義的弱解形式方程式

其中，sr、sz、er、ez分別表示徑向和軸向的應力、應變；Br、Bz、Hr、Hz分別表示徑向和軸向的磁通量密度和磁場強度；rho_rod表示超磁致伸縮棒的密度；_w,_test分別表示弱解模式的名稱和試探函數。電磁場和應力場相互聯系的本構關系通過設置等式表達式的變量來實現。

如前所述，選擇了實驗最佳預壓應力σ0=8MPa，激勵源為一個760匝，線徑為1mm的銅線圈，電流施加方式為隨時間斜線增大到8A。

基于以上分析，對GMA進行全耦合計算，計算結果如圖4～6。由圖4、5可以看出，在電流強度為8A情況下，超磁致伸縮棒內部磁場強度大約為60KA/m，應變大約為1250ppm，并且在磁致伸縮棒兩端的應變要大于棒中間的應變，這主要是由于磁致伸縮棒兩端的磁場強度要略大于中心位置的磁場強度。

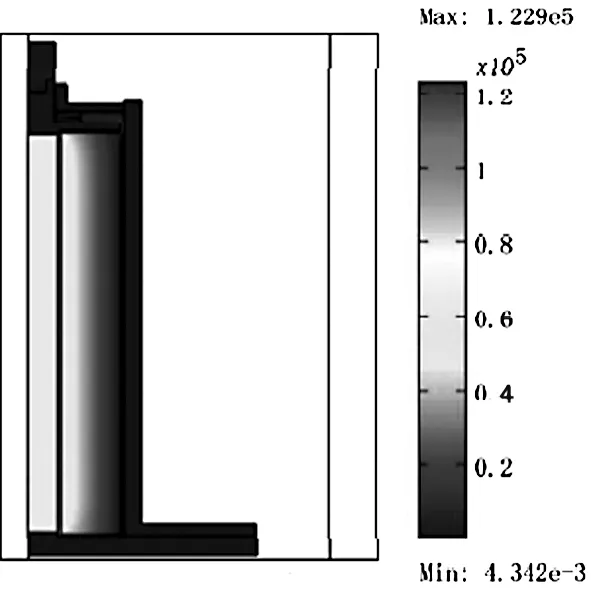
圖4 超磁致伸縮驅動器磁場強度分布計算結果Fig.4 Calculation result of the magnetic field intensity distribution in the GMA

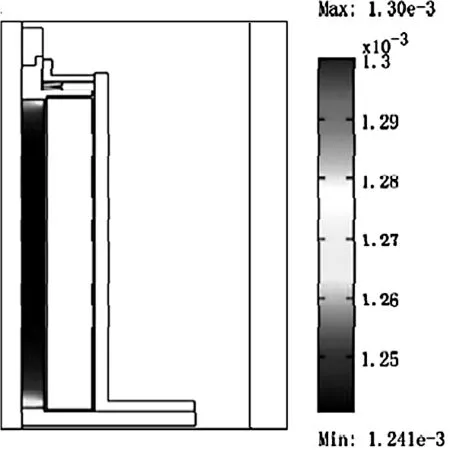
圖5 磁致伸縮棒內部應變分布計算結果Fig.5 Calculation result of the strain distribution in the GMM rod

分別選取磁致伸縮棒幾何中心點和驅動器輸出端面中點，通過COMSOL Multiphysics 3.5計算整個時間歷程的磁致伸縮棒內的磁場強度和驅動器的位移量，計算結果和實驗結果的對比如圖6。

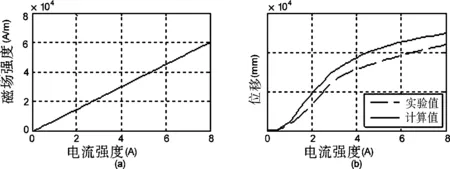
圖6 (a)激勵磁場強度和輸入電流強度之間的關系；(b)輸出位移和輸入電流強度之間的關系Fig.6 (a)Relation between excitation magnetic field intensity and input electric current; (b)Relation between output displacement and input electric current

由于所設計的超磁致伸縮驅動器工作在準靜態環境中，在此沒有考慮渦流損耗，所以電流強度和磁場強度呈線性關系；輸出位移量和試驗值具有相同的變化趨勢，最大誤差不大于10%。

3 結 論

本文根據Jiles-Atherton磁滯模型、二次疇轉模型以及應力-應變模型建立了不考慮渦流損耗的超磁致伸縮驅動器的二維軸對稱非線性有限元模型。通過分別建立機械應力場，電磁場的積分弱解方程，并采用Jiles-Atherton模型來描述兩場之間的耦合關系，在COMSOL Multiphysics 3.5 軟件中進行求解計算，得到的驅動器輸出位移和實驗數據進行了對比，發現誤差較小，說明了該方法的正確性和實用性。由于驅動電流的頻率變化對驅動器的輸出特性有巨大的影響，下一步的工作是研究在計及渦流損耗的情況下，驅動電流的頻率變化對輸出特性的影響。

[1]Engdahl G,Svensson L. Simulation of the magnetostrictive performance of Terfenol-D in mechanical devices[J].Appl Phys,1988,63(8)：3924-3926.

[2]J L Perez-Aparicio,H Sosa. A continuum three-dimensional,fully coupled,dynamic,non-linear finite element formulation for magnetostrictive materials[J].Smart Material and Structure,2004,13(3):493-502.

[3]Kannan Kidambi Srinivasan.Galerkin Finite Element Scheme for Magnetostrictive Structures and Composites[M].Department of Mechanical Engineering, University of Maryland,1997.

[4]Benatar J G,Flatau A B.FEM implementation of a magnetostrictive transducer[J].Smart Structures and Materials,Proceedings of SPIE,2005,5764:482-493.

[5]趙章榮，鄔義杰，顧建新，等.超磁致伸縮執行器的三維非線性動態有限元模型[J].浙江大學學報(工學版)，2008，42(2)：204-208.

Zhao Zhangrong, Wu Yijie,Gu Jianxin,et al.Three-dimensional nonlinear dynamic finite element model for giant magnetostrictive actuators[J].Journal of Zhejiang University(Engineering Science),2008，42(2)：204-208.

[6]趙凱華，陳熙謀.電磁學下冊[M].高等教育出版社，1985，6：793-795.

[7]MAGSOFT Corporation.ATILA Finite Element Analysis for Piezoelectric and Magnetostrictive Structures.User’s Manual,2003,34.

[8]Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(1-2):48-60.

[9]Jiles D C,Atherton D L.Theory of the magnetization process in ferromagnets and its application to the magnetomechanical effect[J].Phys D:Appl Phys,1984,17(6):1265-1281.