鋼鐵污水 TOT項目實物期權法定價案例研究＊

肖 明,張建紅

(1.北京科技大學經濟管理學院北京100083;2.首鋼技術研究院北京100043)

鋼鐵污水 TOT項目實物期權法定價案例研究＊

肖 明1,張建紅2

(1.北京科技大學經濟管理學院北京100083;2.首鋼技術研究院北京100043)

結合鋼鐵污水 TOT項目投資大,工期長,不確定因素多等特點,通過用Black-Scholes定價模型和二項式定價模型,分別進行實例分析,認為鋼鐵水務 TOT項目融資中二項式期權定價模型是一種可資借鑒的評估經營權價格的方法,并簡要分析了實物期權法的局限性和應用建議。

污水 TOT項目;實物期權定價法;Black-Scholes定價模型;二項式定價模型

近年來BOT、TOT模式在國際城市水務行業應用很多,在工業水務行業也有應用,但在國內工業水務行業才剛剛起步。TOT項目經營權價格問題是轉讓協議能否達成的關鍵。

20世紀90年代后期,期權定價理論出現,理論研究者應用實物期權的思想,探討經營權估價的新方法,即期權定價模型,這種方法至今還未實際應用于 TO T項目經營權的評估過程中,是一種新的理論和方法。

一、實物期權法

期權是一種特殊的合約協議,它規定持有者在給定日期或該日期之前的任何時間有權利以固定價格買進或賣出某種資產。期權只有權利而沒有義務,這種權力和義務的不對稱性實際上提供了一種保險的可能。在存在不確定性的條件下,期權是有價值的,而且不確定性越大,期權的價值就越大。如果資產含有期權,那么資產的風險越大,其價值可能也越大。

所謂實物期權,寬泛地說,是期權概念的現實選擇權,是與金融期權相對應的概念。實物期權方法為企業管理者提供了在不確定性環境下進行戰略投資決策的思路,實物期權的一般形式包括放棄期權、擴展期權、收縮期權、選擇期權、轉換期權、混合期權、可變成交價期權以及隱含波動率期權等等。

實物期權的核心思想就是:投資項目的價值不僅來自項目預測的現金流量,還來自于項目的成長機會。用實物期權的方法對投資項目進行評價,投資項目的價值可以分成兩個部分:一部分是不考慮項目期權價值的價值,這正是傳統投資決策方法中的凈現值 N PV;另一部分是投資項目的期權價值 P,因此,引入實物期權理論以后,投資項目的價值可用擴展凈現值 EN PV表示為:EN PV=N PV+P[1]。

實物期權分析方法提供了一種新的項目估價方法,實物期權分析并不是傳統方法的替代物。它將現金流量貼現當作結構單元,并允許根據需要將決策樹綜合進一個更復雜的框架,該框架可以為分析者和決策者提供更有意義的信息。實物期權是動態的戰略決策過程,為作出基于項目評價的“行與不行”的決策提供了很有價值的信息,其中對這些項目進行的評價并不只是為了突出自己的價值,而且也是為了突出和在同一投資組合中的其他競爭項目相比其所具有的相對優點,適用于對投資量大,周期長,階段性強,波動性大的項目進行評價。也就是說,項目價值不只是由當前現金流決定的,而主要是由未來變化決定的。不確定性足夠大的項目,存在或有投資決策的項目以及需要戰略修正的項目一般都可以采用實物期權法進行評價。

二、實物期權法在水務 TOT項目中的應用

水務項目在利用 TOT方式融資時,投資者通過階段的投資,在初期通過較小的投資獲得在以后各階段擴大或縮小投資的權力,進一步確定最佳的退出時機與方式。這就意味著從實物期權的角度看,水務 TOT項目的價值由未來增長期權的可能性帶來,而不是由當前現金流決定的,并且項目在實施過程中要能根據環境等不確定性因素的變化,進行修正和調整項目的經營發展策略。這樣,用實物期權在水務 TOT項目中進行決策就能使投資者在項目順利進行時獲得最大的收益,同時在項目出現不利時可以使投資者的損失降到最小[1]。

若期權只能在某一日(到期日)實施,則稱這種期權為歐式期權,反之,稱為美式期權。一般而言,投資項目中的實物期權屬于可提前執行的美式期權。然而實踐中由于水務 TOT項目合作協議(合約)的約定或相關監管部門的規定,TOT項目中的實物期權大多數不能提前執行,從而呈現歐式期權特征的情況。在這種情況下,在實踐中可以方便地使用B-S模型或二項式模型計算水務TOT項目的實物期權價值。

三、案例分析

某特大型鋼鐵公司集中污水處理廠投資成本的現值為29 000萬元,市場波動率為σ2=25%,目前市場無風險利率為 Kf=2.90%。該公司實行“主輔分離”,該污水廠擬實行 TOT模式融資,預期今后25年現金流的現值為30 000萬元。

(一)B-S期權定價模型分析

在期權定價的研究中,最著名的是由美國經濟學家Black和Scholes所提出的著名的布萊克-斯克爾斯方程,即B-S期權定價模型[1],其表達式為:

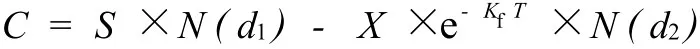
式中:C為買入期權價值;S為當前股票價格,對應項目的標的資產現值;X為投資成本或者執行價格,對應項目的投資額;Kf為年無風險利率;T為距期滿日的時間。

式中:σ為標的資產未來現金流的年度波動率;N(dl)為位于 d l的標準正態分布值;N(d2)為位于d2的標準正態分布值。對適用于期權問題的項目,B-S模型是計算期權值的最簡單的方法。利用實物期權進行水務 TOT項目投資決策時,確定實物期權參數是關鍵的步驟。該 TOT項目采用實物期權法定價所需的參數可確定為:到期期限為 T=25年;執行價格為總的投資額29 000萬元,即 X=29 000萬元;標的資產的價值為 S=30 000萬元;假定市場波動率為σ2=25%;取無風險利率為 Kf=2.90%。將這些參數帶入B-S期權定價模型中計算得:

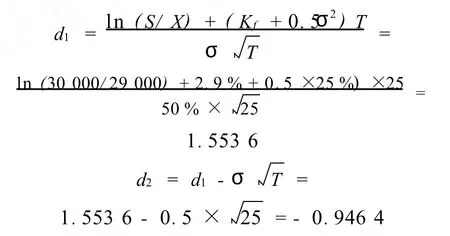
查標準正態分布表得:

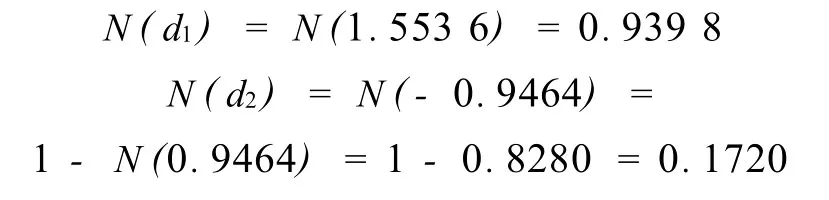
項目的價值為:

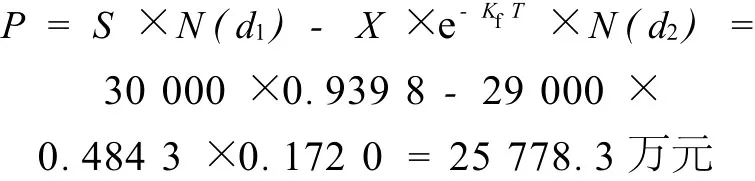
按照傳統的現金流量評價方法,取無風險利率為2.90%,此污水處理項目的收益凈現值為:

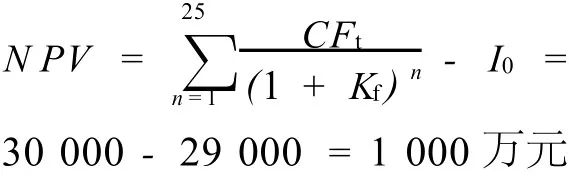
則本項目的投資的潛在價值即擴展凈現值為:

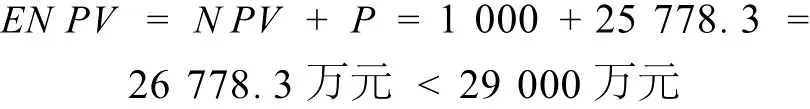
所以,用B-S期權定價模型對該 TOT項目進行評價時,投資者很可能覺得會賠本,因此投資者可能會放棄對該項目進行投資。

(二)二項式模型

二項式模型是目前應用最為廣泛的實物期權估值方法之一。二項式模型是用風險中性定價方法進行定價的。風險中性定價方法假設所有投資者都是風險中性的,在風險中性的經濟環境中,投資者并不要求任何的風險補償或風險報酬,這樣就不需要估計各種風險補償或風險報酬,省略了對風險定價的復雜內容,投資的期望收益率恰好等于無風險利率,投資的任何盈虧經無風險利率的貼現就是它們的現值[2]。

二項式模型以對基礎資產價值變化的一種簡單描述為基礎,即假定在每個時間段,基礎資產價值的變化只能取兩個可能結果中的一個:上升某個百分點或下降某個百分點。比如:假定基礎資產初始價值為V,t0為期初,t1為第一期,t2為第二期,t3為第三期。在每期結束時,前一期的資產價值均可能變化為兩種結果中的一種。在第一個時間段結束后,它要么向上變為Vu,要么向下變為Vd;在此基礎上,當第二個時間段結束后,資產價值變化結果為Vu2、Vud中的一個,或者為Vud、Vd2中的一個;依此類推。這樣的資產價值變化過程可以延伸到多個時間段。于是,這種變化形成了資產價值變化網絡。見圖1[2]。

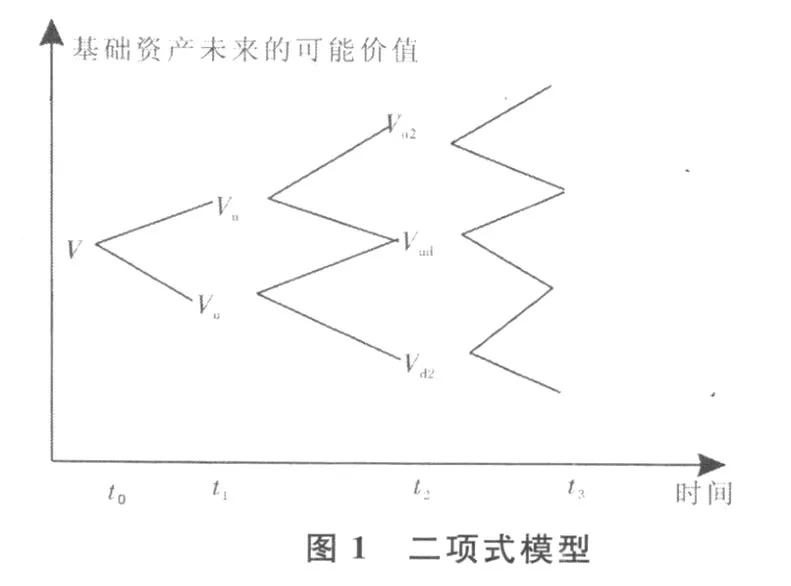
可用風險中性概率的方法來解決用于計算期權值的二項式矩陣。風險中性概率方法的基本方法論涉及了用風險中性概率調整貫穿矩陣的現金流以適應風險,并將現金流以無風險利率進行貼現。不管被估價的期權如何,代表標的資產價值的二項式矩陣有相同的特性,并且可以通過下面討論的方程將其描述出來。向上和向下指數,u和d是標的資產波動率的函數,見如下公式:

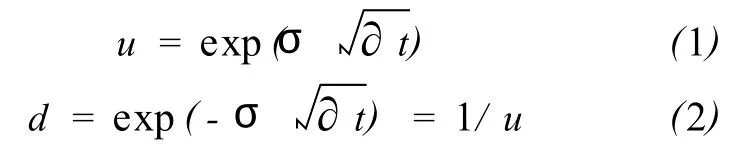
式中:σ為標的自由現金流收益的自然對數的標準差所代表的波動率。

風險中性概率,p的定義如下:

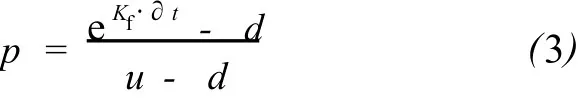
風險中性概率與目標概率不同,風險中性概率僅是一個數學中間物,這一數學中間物可以用無風險利率貼現現金流。

用于構筑二項式樹和計算期權值的輸入參數是:σ,Kf,S,X,T和 ,其中σ是波動指數,Kf是無風險利率,S是標的資產價值的當前值,X是行使期權的成本,?t是被選中用于計算的步長。

事實上,每一個項目中都存在放棄期權。當凈現值(N PV)很少但損失可能會較大時,這一期權是格外有價值的。隨著盈利的不確定性變明確,如果盈利不誘人的話,可以在沒有遭受重大損失的情況下,較早放棄這一項目。可以通過立即廉價出售項目資產或者盡可能地預先安排收縮期權來將損失降到最低點。如果期望收益(標的資產價值)低于項目可挽救價值,即執行價格,這一期權的或有決策應是放棄這一項目[2]。

對于本項目,輸入參數如下:標的資產價值 S=30 000萬元;投資成本 X=29 000萬元;距期滿日的時間 T=25年;標的資產未來現金流的年度波動性σ=50%;無風險年收益率 Kf=2.90%;時間增量步長?t=5年。

其計算實物期權參數,向上指數為

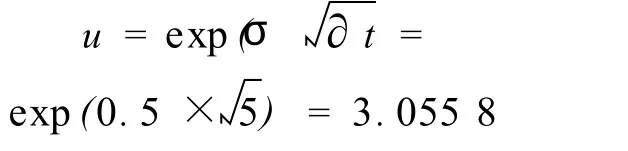
向下指數為:

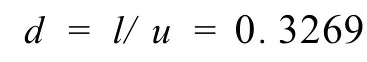
風險中性概率為:

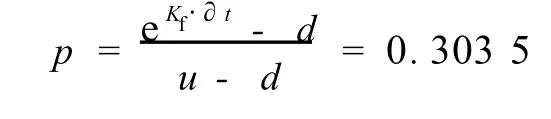
建造二項式樹并且計算每一節點處的資產價值。建造一個二項式樹,未來25年的時間增量步長為5年,利用該步長來計算期權使用壽命內的資產價值。從左邊第一個節點的開始 S開始,將其與向上指數和向下指數相乘,分別得到第一個時間步長的Su(30 000×3.055 8=91 765.04萬元)和 Sd(30 000×0.326 9=9 807.615萬元)。向右移動,繼續按類似的方式計算出二項式樹的每個節點的Su和Sd直到最后一時間步長。每一節點的頂端值代表這一節點的資產價值。見圖2。

用向后歸納法計算出二項式樹每一節點的實物期權值。

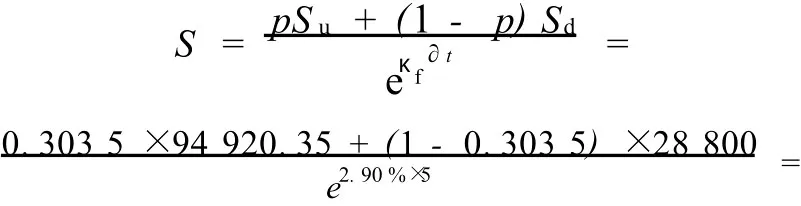
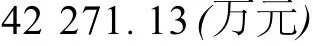
圖2顯示了用向后歸納法得出的二項式樹每一節點的實物期權值(底部數字表示)。每一節點代表所得到的最大價值。在每節點可以選擇放棄期權從而獲得對應的資產凈值(標下劃線的數字)或繼續保持這一期權直到它期滿。最后,使用上述的方法一直進行到時間步長為零完成期權估算的二項式樹。

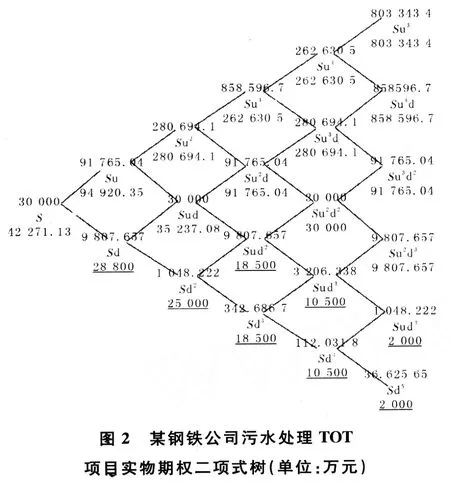
解析結果,基于現金流量貼現法并沒有考慮靈活性因素的項目收益是30 000萬元,但投資成本是29 000萬元,這樣該項目的凈現值僅為相對較小的1 000萬元。然而,實物期權分析卻顯示項目的總價值為42 271.13萬元,由于放棄期權的存在,產生了13 271.13萬元的附加值。因此,由于放棄期權的出現,該項目的凈現值是原來的13倍多。

(三)結果分析

對B-S模型和二項式模型估價的結果進行比較,結果見表2。

表2 B-S模型和二項式模型估價的比較

B-S模型提供了不需要將期權壽命分成時間增量的閉合式分析解答,最適合于只能在到期日執行的看漲期權。

二項式是目前應用最為廣泛的實物期權估值方法之一,需對期權壽命進行分解。當方程中的時間增量增加后,二項式解答將接近B-S模型的結果。五個或者六個時間增量就足夠了,并且最后的實物期權值與B-S的解答極不相同。與包含在估算大量輸入參數中的許多錯誤相比,模型框架中的時間增量對最終期權值的影響是無關緊要的[2]。

二項式期權在每節點可以選擇放棄期權從而獲得對應的資產凈值或繼續保持這一期權直到它期滿。正是由于放棄期權的存在,二項式期權一般比B-S模型要多產生一定的的附加值。

實物期權法集中分析項目的不確定性因素,用概率的語言表述現金流的計算范圍,計算簡潔。然而某些參數比較抽象,如σ,而且未來各年可能都不一樣。目前,其實用性還有待進一步研究[3]。

四、結論與建議

第一,相對B-S模型而言,使用二項式模型估價對水務 TO T投融資雙方更為公平合理,但要把握參數的合理選取。

第二,應充分了解實物期權本身所存在的局限性,如模型本身的假設條件,標的資產價格和其價格變化標準差不易準確獲取,標的資產缺乏市場流通性,非系統性風險等。對于這些局限性,需要決策者提高企業基礎性管理水平,通過學習與實踐,在提高理論水平的基礎上,積累必要的經驗來加以克服。

第三,管理層是實物期權價值能否實現的關鍵。如果一些項目本身 N PV是負的,在做出投資決策時,管理層考慮到了項目的期權價值,決定予以項目投資。但在實際執行中,卻不能根據信息的變化,及時做出進一步預測,那么該期權價值將無法得到實現。即使開始看來是正確的決策,最后也可能失敗。因此應謹慎運用實物期權方法,而應代之以科學決策,防止項目評估中因為高估期權價值而造成的投資失誤。

[1] 劉 巍,張雪平.實物期權在BOT水電項目投資中的應用[J].技術經濟,2007,26(12):74-77.

[2] 馬冬鳴.項目估價的實物期權應用模型研究[D].北京:北京科技大學,2008.

[3] 龍 敏.高速公路經營權估價理論與方法綜述[J].重慶交通大學學報:社科版,2007,7(3):23-25.

Study on Pricing with Real Option Approach for Wastewater TOT Project of Steel-making Enterprise

XIAO Ming,ZHANG Jian-hong
(1.School of Economics and Management,Beijing University of Science and Technology,Beijing 100083,China;2.Shougang Research Institute of Technology,Beijing 100043,China)

It’s very important to p rice the valuation of management rights of TOT project for right decision to invest TOT project.Considering with some traits in wastewater TOT project of Steel-making enterprise,such as huge investment,long term of construction and many uncertain aspects,analyzing a real case disting uishingly with Black-Scholes model and the binomial p ricing model,this paper concludes that the binomial p ricing model is a competent app roach to p rice the valuation of management rights of wastewater TOT project for Steel-making enterprise.A t last,it analyses the limitations of ROA(Real Option App roach)tersely and gives some advice.

wastewater TOT project;ROA;Black-Scholes model;the binomial p ricing model

F2

A

10.3963/j.issn.1671-6477.2010.01.012

2009-06-20

肖 明(1963-),男,蒙古族,內蒙古通遼市人,北京科技大學經濟管理學院財務與會計系教授,博士,博士生導師,主要從事公司財務與會計理論研究;張建紅(1982-),男,湖北省天門市人,碩士,首鋼技術研究院工程師,主要從事水務技術與項目管理研究。

國家自然科學基金“基于模糊測度的鋼鐵產品環境影響評價理論與方法研究”(70672102)

(責任編輯 易 明)