重視情境教學　調動學生思維

杜修鵬

數學的發展一再證明:“問題是數學的心臟。”這么說,數學的發展過程就是不斷提出問題解決問題的過程。數學教育的核心是培養學生解決數學問題的能力。那么教師如何合理運用問題教學呢?創設問題情境,巧妙設置疑問,激發學生的認知潛能,實際上即為問題的提出、分析和解決的過程。在中學數學的教學中，情境教學因其能有效提高課堂效率，培養學生認知能力、主動學習能力、分析問題解決問題能力而倍受廣大數學教師的鐘愛。

一.對情景教學的理解

在實際問題的情景下，模仿數學家思維活動過程，挖掘數學認識動機、內在聯系以及知識的產生和發展的情節為主體的教學手段是新課標要求下一種全新的教學模式。在運用這種教學方法的過程中必須注意以下幾點：第一，構造思維活動的情節時，以探索啟發為主不一定是遵守形式邏輯規則的嚴格思維，而是運用合理的推理和擬真推理進行教學；第二，設計教學活動過程必須聯系學生的情感、意志、水平，使學生在興奮狀態下經歷潛伏——存疑——豁然開朗的過程（也就是提出問題——試一試——不斷嘗試中增強信心）——下決心證明——得到正確結果的過程；第三，構成活動情節的類型有：（1）概念的形成過程；（2）方法的思考過程；（3）結果的探究過程。教學上應按這樣的過程去設計教法，才能達到數學情境教學的目的。

二.實施情境教學的具體做法

數學情境教學的實施大致可以用如下框圖進行：

下面就以勾股定理一課為例加以說明。

1.創設問題情境

是指根據日常生活的實際問題、數學趣味問題等，挖掘出一個數學問題。如在講授勾股定理時，設置問題情境：相傳2500年前，畢達哥拉斯有一次在朋友家做客時，發現朋友家的用磚鋪成地面中反映了直角三角形三邊的某種數量關系。（出示圖形）你能發現什么？

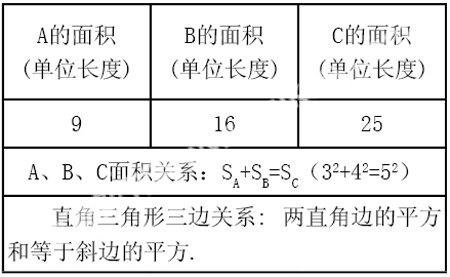
問題1：.A、B、C的面積有什么關系？

2.嘗試學習

是指在教師的指導下，通過自己的嘗試，探究問題的解決。嘗試的目的是讓學生自己動手動腦，以主動的姿態參與學習知識的全過程。學生通過觀察可以得出結論。

結論1：S_A+S_B=S_C

問題2：等腰直角三角形的三邊之間有什么關系？（學生思考作答）

結論2：兩直邊的平方和等于斜邊的平方。

3.深入探究

是指學生處于嘗試學習的時候，可能會遇到一些疑問，為了幫助學生克服這些疑問，教師可以設置相關的問題，學生通過探究，得到新的結論。

問題3：任意一個直角三角形三邊之間是否有上面的關系？（出示圖形）

這時學生的思維又一次被調動起來，頭腦處于興奮狀態，進入解決問題的高潮。

4.解決問題

這是情境教學的最后階段，是整節課的高峰期。處于興奮狀態的學生自己動腦、動手去解決他們想解決而未解決的問題，因而思維特別活躍，對問題急于弄個水落石出。因而教師此時應用鼓勵的目光和語言去幫助學生，使他們順利解決問題。通過上面的探究過程，可得結論：如果直角三角形的兩直角邊長分別為a,b,斜邊長為c,那么a²+b²=c²

三.情境教學在數學教學中的意義

根據多年的教學情況看，使用情境教學法至少有如下好處：

1、數學情境教學一開始就提出了對全堂課起關鍵作用的、學生自己能夠解決的、富有挑戰性的問題，激發學生的濃厚學習興趣并以積極的態度去解決所提出的問題，這就形成了“要求學習”的情境，為后面課的展開奠定了良好的基礎。

2、創設了問題情境。問題是思維的出發點，有了問題才會去思考，對學生來說提出一些他們想解決而未解決的、富有挑戰性、趣味性的問題更能激發學生的向心力，促使他們積極思考。

3、從實施過程來看，全體學生真正做到了動手、動腦、動口，積極參與教學的全過程，從不自覺到自覺地發揮了他們的思維能力和創造能力。

4、在教學中使以學生為主體教師為主導的教學原則得到了很好的貫徹。學生的學習是主動的學習，始終貫穿著學生的自主活動，充分發揮了學生在學習過程中的主體作用。讓學生真正成為學習的主人，使他們去探索、去發現、去獲取，其結果使教學系統中的教與學控制在最佳狀態——學困生在練習中及時得到幫助，中等以上的學生也有進一步發揮的機會，從而教師更能從中了解學生的實際情況并及時調節教學環節。

5、數學情境教學重視發展學生的思維訓練，能讓學生越學越聰明。情境教學強調概念的形成過程、解題的分析思考過程和規律的揭示過程，常把學生的思維集中到問題的探索研究上來，就是連差生也容易想進去，學進去，從中嘗到思考的樂趣。逐步愛上數學，真正做到把興趣還給學生，把魅力還給數學。

6、數學情境教學重視調動學生的非智力因素，為學生建立了一個良好的心理環境。在學習中最活躍的成份是興趣，而情境教學恰好提供了培養興趣的基地。當學生解決了他們想解決而未解決的問題時，經教師的表揚會產生一種愉悅的心境，享受成功帶來的快樂，這對培養學生對數學的興趣毫無疑問是有積極意義的。

（作者聯通：717300陜西省子長縣齊家灣中學）