基于非負(fù)稀疏編碼的位置細(xì)胞反饋環(huán)路學(xué)習(xí)模型

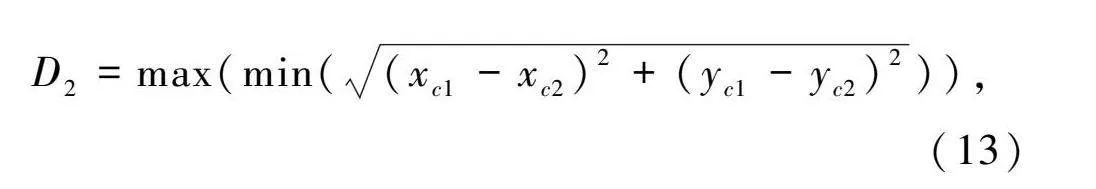
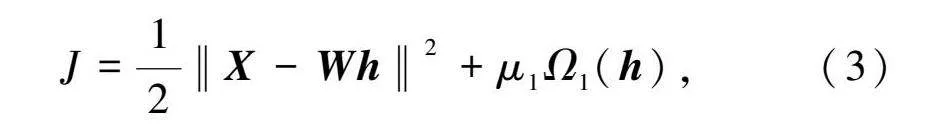
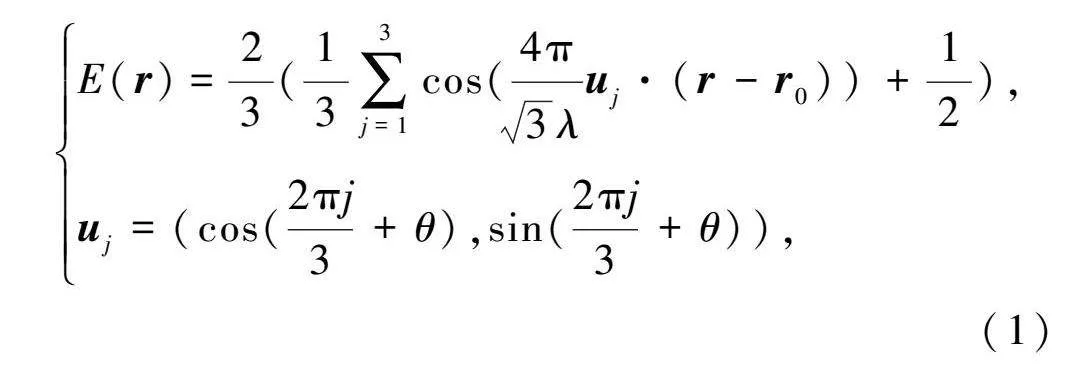
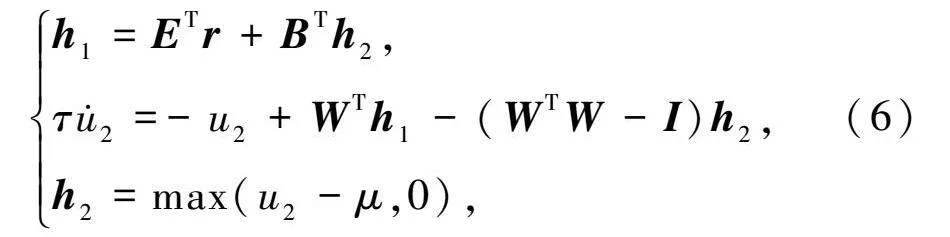
摘要： 為了探究大腦導(dǎo)航編碼的神經(jīng)機(jī)制，聚焦內(nèi)嗅皮層與海馬體之間的神經(jīng)連接進(jìn)行模型研究。生理學(xué)證據(jù)顯示，內(nèi)嗅皮層與海馬體之間存在顯著的反饋回路連接，兩者的空間編碼細(xì)胞在導(dǎo)航行為中表現(xiàn)出高度關(guān)聯(lián)性。基于這一基礎(chǔ)，建立了反饋循環(huán)網(wǎng)絡(luò)模型，將內(nèi)嗅皮層的柵格細(xì)胞與弱空間細(xì)胞作為網(wǎng)絡(luò)輸入，連接到海馬體的位置細(xì)胞與顆粒細(xì)胞，并采用非負(fù)稀疏編碼進(jìn)行學(xué)習(xí)。實(shí)驗(yàn)結(jié)果表明：該反饋學(xué)習(xí)模型可以快速捕獲細(xì)胞的空間調(diào)諧特性，僅使用弱空間細(xì)胞作為輸入，也可以通過(guò)反饋環(huán)路學(xué)習(xí)到海馬位置細(xì)胞對(duì)空間的單峰選擇性，說(shuō)明反饋編碼機(jī)制在優(yōu)化空間表示中發(fā)揮著關(guān)鍵作用。總之，該模型可能是大腦導(dǎo)航系統(tǒng)生成精確空間編碼的重要細(xì)胞機(jī)制之一。

關(guān)鍵詞： 內(nèi)嗅皮層； 海馬體； 柵格細(xì)胞； 位置細(xì)胞； 反饋循環(huán)； 非負(fù)稀疏編碼

中圖分類號(hào)： TP301

文獻(xiàn)標(biāo)志碼： A

文章編號(hào)： 1671-6841（2025）01-0031-09

DOI： 10.13705/j.issn.1671-6841.2023188

A Place Cell Recurrent Loop Learning Model Based on

Non-negative Sparse Coding

REN Menghui^1，2， WANG Dongshu^1，2

（1.School of Electrical and Information Engineering，Zhengzhou University， Zhengzhou 450001， China;

2.Innovation Center of Intelligent Systems，Longmen Laboratory， Luoyang 471000， China）

Abstract： To explore the neural mechanisms of brain navigation encoding， focus was placed on the neural connections between the entorhinal cortex and the hippocampus for model research. Physiological evidence showed that significant feedback loop connections existed between the entorhinal cortex and the hippocampus， with the spatial encoding cells of both being highly correlated in navigational behavior. Based on this foundation， a feedback loop network model was established， where grid cells and weak spatial cells from the entorhinal cortex were taken as network inputs， connected to place cells and granule cells in the hippocampus， and non-negative sparse coding was employed for learning. Experimental results indicated that the feedback learning model could rapidly capture the spatial tuning properties of these cells. Even when only weak spatial cells were used as inputs， the hippocampal place cells′ unimodal selectivity to space could be learned through the feedback loop， suggesting that the feedback encoding mechanism played a key role in optimizing spatial representation. In summary， the model might be one of the important cellular mechanisms for generating precise spatial encoding in the brain′s navigation system.

Key words： entorhinal cortex; hippocampus; grid cell; place cell; feedback loop; non-negative sparse encoding

0引言

文獻(xiàn)［1］發(fā)現(xiàn)大鼠海馬體中部分神經(jīng)元的放電模式隨著大鼠在環(huán)境中的位置而發(fā)生規(guī)律性變化，表明了這些神經(jīng)元對(duì)空間位置信息高度敏感，因此被稱為“位置細(xì)胞”，其放電場(chǎng)稱為“位置野”。文獻(xiàn)［1］指出，位于大腦海馬體中的位置細(xì)胞是動(dòng)物構(gòu)建認(rèn)知地圖的基礎(chǔ)，因此涉及空間感知和導(dǎo)航的大腦區(qū)域引起了計(jì)算神經(jīng)科學(xué)家的廣泛關(guān)注。

鄭 州 大 學(xué) 學(xué) 報(bào) （理 學(xué) 版）第57卷第1期任夢(mèng)輝，等：基于非負(fù)稀疏編碼的位置細(xì)胞反饋環(huán)路學(xué)習(xí)模型

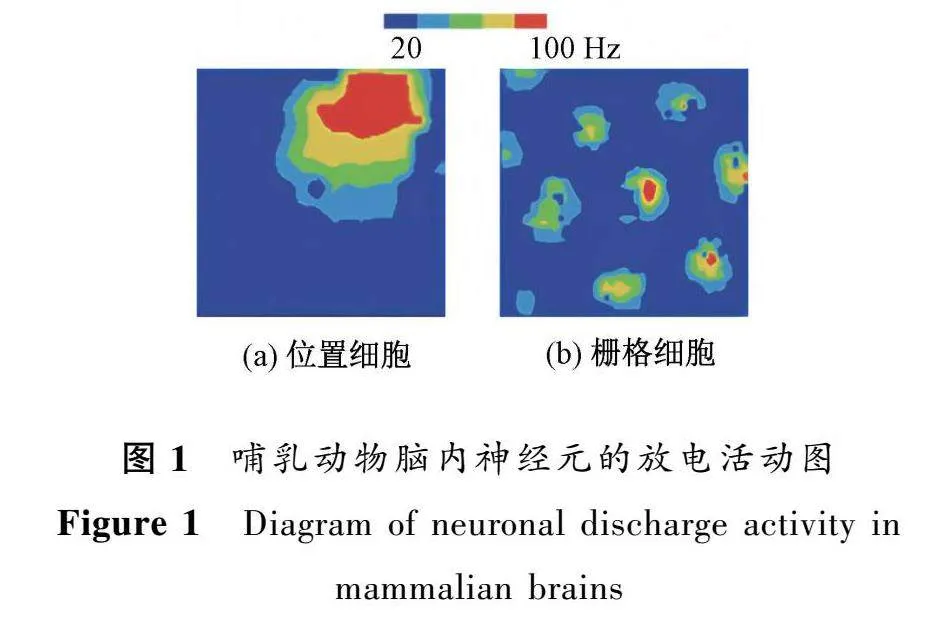
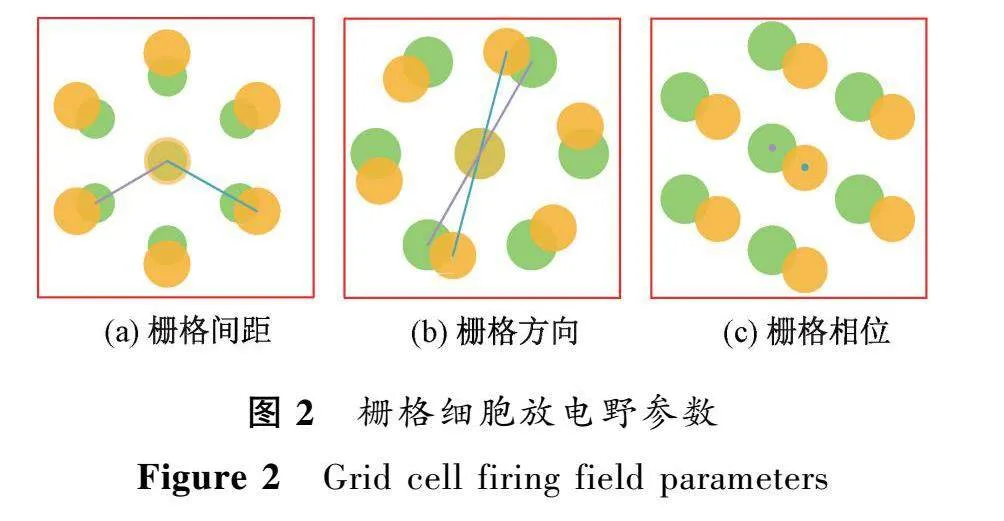
在海馬體中，每個(gè)位置細(xì)胞通常在小環(huán)境中表現(xiàn)單一的位置野^［2］（圖1（a）），相鄰的位置細(xì)胞對(duì)不同的空間信息具有選擇特性，因此海馬體中的位置細(xì)胞群對(duì)整個(gè)環(huán)境具有表征作用，可以實(shí)現(xiàn)對(duì)空間位置的精確編碼。然而，與位置細(xì)胞不同，海馬體齒狀回中的顆粒細(xì)胞具有多個(gè)離散的放電位置，沒(méi)有明確的空間周期性^［3］。這可能與顆粒細(xì)胞參與的神經(jīng)網(wǎng)絡(luò)環(huán)路有關(guān)。內(nèi)嗅皮層位于顳葉并與海馬體相鄰，其中也包含多類對(duì)空間信息具有不同編碼特性的神經(jīng)元，如具有結(jié)構(gòu)化特性的柵格細(xì)胞^［4］和僅具有空間選擇性但沒(méi)有結(jié)構(gòu)化排列的弱空間細(xì)胞^［5］。柵格細(xì)胞在多個(gè)區(qū)域形成穩(wěn)定的六邊形放電野（圖1（b）），每個(gè)放電野位于正六邊形柵格的頂點(diǎn)，因此被稱為“柵格細(xì)胞”。內(nèi)嗅皮層中柵格細(xì)胞的這種周期性空間放電模式可以用柵格間距、柵格相位和柵格方向等參數(shù)來(lái)描述（圖2所示）。

研究顯示，包含柵格細(xì)胞和弱空間細(xì)胞在內(nèi)的內(nèi)嗅皮層輸入是海馬體的主要輸入來(lái)源^［6］。為了解釋基于柵格細(xì)胞連接產(chǎn)生位置細(xì)胞的機(jī)制，研究人員提出了多種數(shù)學(xué)和計(jì)算模型。文獻(xiàn)［7］首先提出平移轉(zhuǎn)換模型，通過(guò)柵格細(xì)胞的位移來(lái)編碼頭部方向信息，并結(jié)合柵格圖的空間周期性來(lái)生成位置細(xì)胞。但是該模型難以解釋多峰和異形位置野的生成。文獻(xiàn)［8］建立了吸引子網(wǎng)絡(luò)模型，允許柵格圖根據(jù)頭部方向作平移變換，但對(duì)細(xì)胞動(dòng)力學(xué)和突觸可塑性的建模不足。文獻(xiàn)［9］提出一體化神經(jīng)網(wǎng)絡(luò)模型，利用神經(jīng)網(wǎng)絡(luò)以柵格細(xì)胞和頭部方向細(xì)胞作為輸入來(lái)產(chǎn)生位置細(xì)胞，但是由于網(wǎng)絡(luò)結(jié)構(gòu)復(fù)雜，解釋性不足。

文獻(xiàn)［10］研究發(fā)現(xiàn)，稀疏編碼可以優(yōu)化生成視覺(jué)皮層中簡(jiǎn)單細(xì)胞的視接收野。文獻(xiàn)［11］研究證實(shí)，稀疏編碼可以解釋大腦多個(gè)區(qū)域內(nèi)廣泛存在的稀疏神經(jīng)元響應(yīng)。然而，尚未有研究將具有非負(fù)約束的稀疏編碼應(yīng)用于基于內(nèi)嗅皮層-海馬體反饋環(huán)路的網(wǎng)絡(luò)模型中。本文構(gòu)建了一個(gè)內(nèi)嗅皮層-海馬體反饋循環(huán)網(wǎng)絡(luò)學(xué)習(xí)模型，其中使用內(nèi)嗅皮層作為輸入，同時(shí)對(duì)神經(jīng)元響應(yīng)和連接權(quán)重添加非負(fù)約束，并研究了在此模型中引入非負(fù)稀疏編碼對(duì)學(xué)習(xí)位置細(xì)胞特性的效果。

1實(shí)驗(yàn)原理及方法

1.1實(shí)驗(yàn)環(huán)境

在1m×1m的二維環(huán)境中，將其離散為32×32的網(wǎng)格，用1 024×1的矢量表示整個(gè)環(huán)境空間。環(huán)境中智能體的任意位置用r表示，r是一個(gè)1 024×1的矢量，其中僅有一個(gè)元素非零。在這個(gè)32×32網(wǎng)格中，有一個(gè)格子被標(biāo)記為黑色，表示智能體的位置。每個(gè)格子代表環(huán)境中的一個(gè)離散位置，而整個(gè)網(wǎng)格則代表了整個(gè)環(huán)境空間。

1.2柵格細(xì)胞模型

柵格細(xì)胞的計(jì)算模型主要包括振蕩干涉模型、連續(xù)吸引子網(wǎng)絡(luò)模型和自適應(yīng)模型三大類^［12］。其中振蕩干涉模型^［13］是目前公認(rèn)的主流和經(jīng)典模型。振蕩干涉模型的核心思想是通過(guò)柵格細(xì)胞中多個(gè)空間定向的振蕩器相互干涉和疊加，產(chǎn)生定位的六邊形空間圖譜。這一模型可以解釋柵格細(xì)胞六邊形放電野的生成機(jī)制，也與動(dòng)物實(shí)驗(yàn)結(jié)果高度吻合。具有代表性的振蕩干涉模型包括文獻(xiàn)［14］提出的雙軸模型、文獻(xiàn)［15］提出的擴(kuò)展振蕩模型等，這些模型通過(guò)調(diào)節(jié)各個(gè)參數(shù)在不同條件下產(chǎn)生不同尺度的柵格圖。因此，振蕩干涉模型在解析柵格細(xì)胞空間編碼和生理機(jī)制上發(fā)揮著核心作用。

本文采用振蕩干涉模型的柵格細(xì)胞作為內(nèi)嗅皮層的輸入，

E（r）=23（13∑3j=1cos（4π3λu·（r-r））+12），

u=（cos（2πj3+θ），sin（2πj3+θ）），（1）

式中：E（r）表示網(wǎng)格細(xì)胞在r=（x，y）位置處的響應(yīng)；λ表示柵格間距；u是一個(gè)單位向量；r=（x，y）表示柵格相位；θ表示柵格方向。柵格細(xì)胞響應(yīng)被歸一化為［0，1］。由于正六邊形的周期性，柵格方向位于［0，π/3）內(nèi)，沿坐標(biāo)軸的相位小于柵格間距，0≤x，y≤λ。由公式（1）建立的柵格細(xì)胞模型如圖3所示。

大量的電生理實(shí)驗(yàn)研究顯示，柵格細(xì)胞的間距范圍一般在30～100cm。其中，文獻(xiàn)［16］于2022年發(fā)現(xiàn)柵格間距之間存在離散的聚類分布，不同聚類之間的間距比值約為1.4。因此，本研究在建立柵格細(xì)胞模型時(shí)，選取網(wǎng)格間距的最小值為30cm，比例系數(shù)選擇接近實(shí)驗(yàn)值的1.4，柵格間距個(gè)數(shù)為4。該參數(shù)選擇既可以保證模擬柵格細(xì)胞空間編碼范圍包括智能體行為相關(guān)的大部分尺度，同時(shí)也符合實(shí)驗(yàn)觀測(cè)到的柵格空間表示的模塊化和對(duì)數(shù)關(guān)系特征。基于分布參數(shù)的設(shè)定構(gòu)建了柵格細(xì)胞模型，并研究了柵格參數(shù)的稀疏性對(duì)模型學(xué)習(xí)位置細(xì)胞空間特征的影響。

假設(shè)有N個(gè)不同的柵格間距，那么柵格間距的分布為30cm， 42cm，…，30×1.4^N-1cm。對(duì)于每種柵格間距都有不同的柵格方向，本文以均勻采樣的方式從［0，π/3）范圍內(nèi)為柵格細(xì)胞模型選擇六個(gè)方向。假設(shè)每種柵格間距有N個(gè)不同的柵格方向，那么柵格方向的分布為0，π/3N，…，（N-1）π/3N。通常，柵格細(xì)胞的相位小于柵格間距，能保持放電野的連續(xù)性和正六邊形結(jié)構(gòu)，有效編碼空間信息。相位大于柵格間距會(huì)導(dǎo)致放電野跳躍到下一個(gè)周期，破壞空間編碼特性，影響導(dǎo)航和認(rèn)知地圖的形成。因此本文選擇六個(gè)柵格相位。假設(shè)沿坐標(biāo)軸有N和N個(gè)相位，分別以均勻采樣方式從［0，λ）范圍內(nèi)選取柵格相位。例如，沿x軸的相位分布為0，λ/N，…，（N-1）λ/N。因此，柵格細(xì)胞數(shù)N可以表示為

N=NNNN，（2）

如圖3顯示了不同柵格參數(shù)的柵格細(xì)胞模型。

1.3弱空間細(xì)胞模型

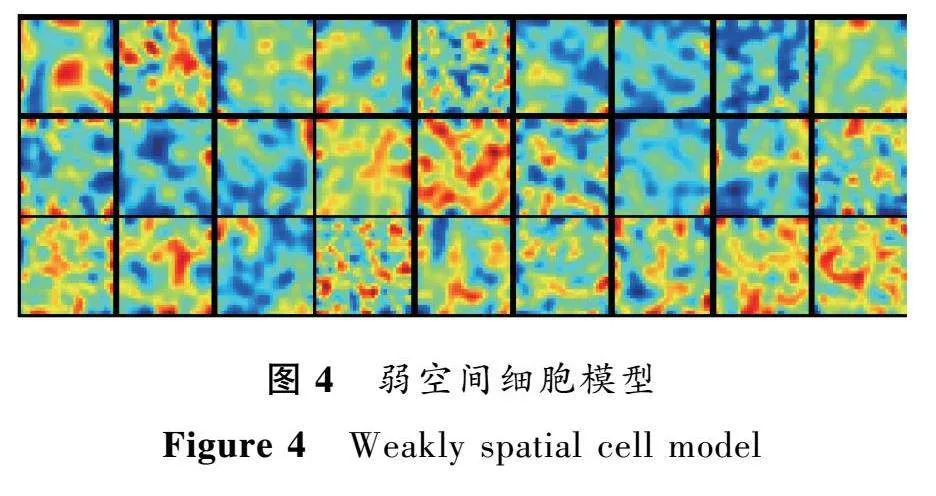
除了具有明確正六邊形排布的柵格細(xì)胞，內(nèi)嗅皮層中還包含對(duì)空間信息具有響應(yīng)但沒(méi)有明確放電野結(jié)構(gòu)的神經(jīng)元，這類神經(jīng)元被統(tǒng)稱為“弱空間細(xì)胞”。2017年，文獻(xiàn)［17］通過(guò)對(duì)海馬體區(qū)神經(jīng)活動(dòng)的多點(diǎn)電生理記錄，發(fā)現(xiàn)弱空間細(xì)胞對(duì)驅(qū)動(dòng)海馬體位置細(xì)胞的形成起關(guān)鍵性調(diào)控作用。

本文使用文獻(xiàn)［5］的方法對(duì)弱空間細(xì)胞進(jìn)行建模，如圖4所示。

1.4非負(fù)稀疏編碼

編碼稀疏性是神經(jīng)系統(tǒng)對(duì)信息進(jìn)行高效壓縮編碼的重要原則之一。文獻(xiàn)［18］明確提出稀疏編碼理論，并指出稀疏表示可以產(chǎn)生簡(jiǎn)單細(xì)胞的視覺(jué)特征。最近的研究表明，海馬區(qū)神經(jīng)元對(duì)空間位置具有高度稀疏的編碼分布^［19］。因此，本文在模型中添加編碼稀疏性約束，優(yōu)化每個(gè)神經(jīng)元對(duì)位置信息的稀疏響應(yīng)分布。這種稀疏性約束可能有助于生成更符合實(shí)際的位置細(xì)胞編碼模式。

稀疏編碼通過(guò)尋找感覺(jué)輸入的線性表示，以最小化重構(gòu)誤差解決最優(yōu)特征表示，即使用最少的神經(jīng)元表示輸入，實(shí)現(xiàn)對(duì)輸入的最佳重構(gòu)。稀疏編碼的目標(biāo)函數(shù)可以表示為

J=12‖X-Wh‖²+μΩ（h），（3）

其中：X表示輸入向量；W表示權(quán)重矩陣；h表示稀疏編碼的結(jié)果；Ω（h）表示稀疏性懲罰項(xiàng)；μ是衡量重構(gòu)誤差和稀疏性的參數(shù)。在神經(jīng)網(wǎng)絡(luò)中，W表示網(wǎng)絡(luò)層間的連接權(quán)重，h表示神經(jīng)元響應(yīng)，Wh項(xiàng)表示模型重構(gòu)。通過(guò)求解目標(biāo)函數(shù)的最小值，得到權(quán)重連接矩陣W以及輸入的稀疏表示h。應(yīng)用梯度下降法得到動(dòng)力學(xué)方程和學(xué)習(xí)規(guī)則，

h·=WT（X-Wh）-μΩ（h），

ΔW∝〈（X-Wh）hT〉，（4）

通常Ω（·）選擇絕對(duì)值函數(shù)。在神經(jīng)網(wǎng)絡(luò)中，使用閾值和局部競(jìng)爭(zhēng)方法來(lái)實(shí)現(xiàn)

τu·=-u+WTX-（WTW-I）h，

h=max（u-μ，0），如果u>0，

min（u+μ，0），如果u<0，（5）

式中：I表示單位矩陣；τ表示時(shí)間常數(shù)；u類似于細(xì)胞的膜電位，本文取值為10mV；μ表示閾值（非負(fù)稀疏常數(shù)），取0.3，限制W和h非負(fù)。

1.5內(nèi)嗅-海馬反饋環(huán)路模型

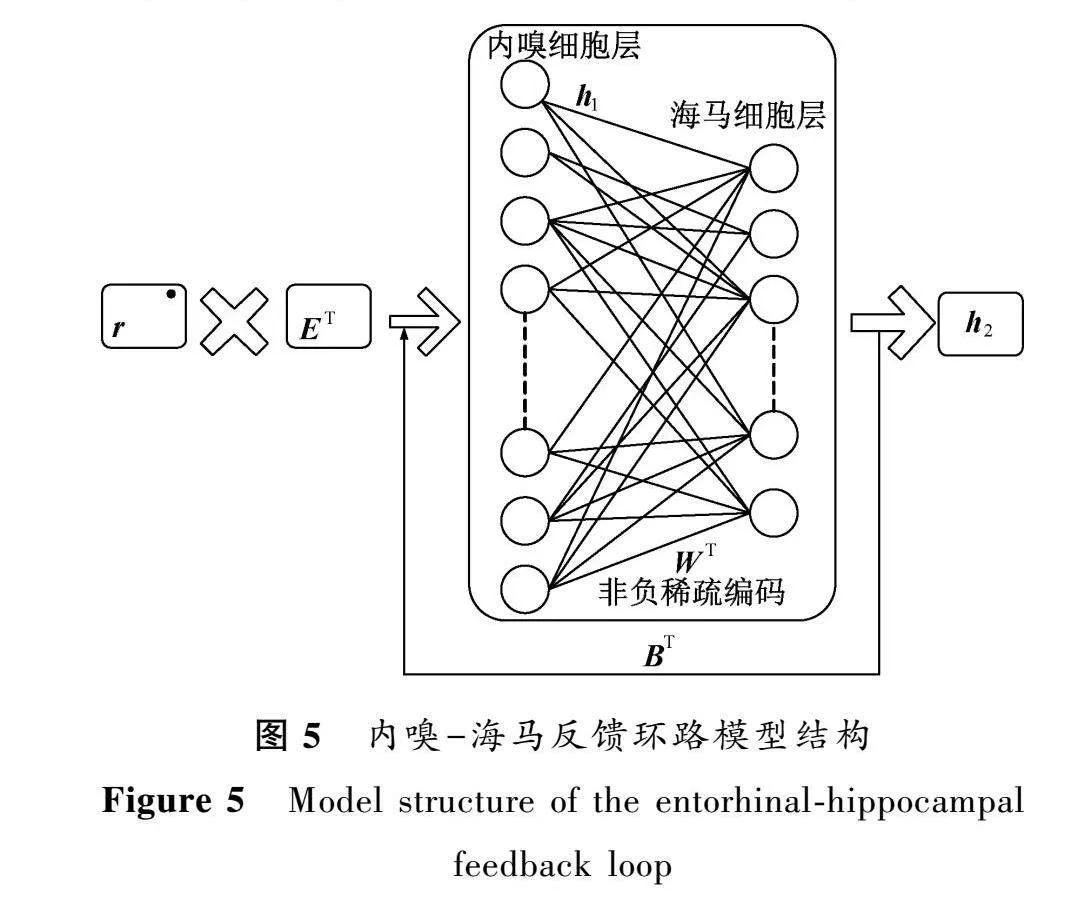
本文提出了一種基于雙層神經(jīng)網(wǎng)絡(luò)的反饋模型，用于產(chǎn)生和學(xué)習(xí)內(nèi)嗅細(xì)胞和海馬細(xì)胞的激活。該模型根據(jù)給定空間位置，在內(nèi)嗅細(xì)胞層生成位置野響應(yīng)，并將其作為輸入傳遞到海馬細(xì)胞層。然后，海馬細(xì)胞層的神經(jīng)元響應(yīng)再以非負(fù)的形式反饋給輸入細(xì)胞層，影響其位置野的學(xué)習(xí)過(guò)程，如圖5所示。

模型中：r表示空間位置；E表示神經(jīng)網(wǎng)絡(luò)中所有內(nèi)嗅細(xì)胞的放電野；h表示內(nèi)嗅細(xì)胞響應(yīng)；B表示海馬細(xì)胞層到內(nèi)嗅細(xì)胞層的反饋連接矩陣。基于公式（5），可以獲得該模型的動(dòng)力學(xué)方程

h=ETr+BTh，

τu·=-u+WTh-（WTW-I）h，

h=max（u-μ，0），（6）

式中：τ表示海馬細(xì)胞的時(shí)間常數(shù)，本文取值為0.8ms；μ表示海馬細(xì)胞的激活閾值；（WTW-I）表示海馬細(xì)胞間的循環(huán)連接，通過(guò)局部競(jìng)爭(zhēng)算法可有效解決稀疏編碼的問(wèn)題。其中海馬細(xì)胞響應(yīng)h和連接權(quán)重矩陣W被限制為非負(fù)。

前饋連接權(quán)重矩陣W和反饋連接權(quán)重矩陣B的學(xué)習(xí)規(guī)則相似。首先定義誤差為輸入h與利用W和輸出h重構(gòu)的h′之差，然后根據(jù)Hebb學(xué)習(xí)規(guī)則對(duì)權(quán)重矩陣進(jìn)行更新。前饋連接權(quán)重矩陣的學(xué)習(xí)規(guī)則為

ΔW=α（h-Wh）hT，（7）

反饋連接權(quán)重矩陣的學(xué)習(xí)規(guī)則為

ΔB=β（h-Bh）hT，（8）

式中：α和β分別為前饋連接矩陣和反饋連接矩陣的學(xué)習(xí)率，本文取值分別為0.03和0.0003。

使用模型動(dòng)力學(xué)方程得到的海馬細(xì)胞響應(yīng)，由于存在細(xì)胞間的循環(huán)連接，本文采用反向相關(guān)方法擬合海馬位置細(xì)胞的位置野，

Q=hr+hr+…+hrh+h+…+h，（9）

式中：Q表示海馬細(xì)胞，r，r，…，r表示隨機(jī)采樣的n個(gè)位置，為了能夠有足夠多的數(shù)據(jù)支撐，本文取值為10⁵，h，h，…，h表示對(duì)應(yīng)位置的海馬細(xì)胞響應(yīng)。

為了表征學(xué)習(xí)到的位置細(xì)胞對(duì)環(huán)境空間的表征程度，需要獲得位置野的中心和半徑，對(duì)位置野進(jìn)行函數(shù)擬合，

G（r）=χe^{-ln5‖r-r^}‖R^，（10）

式中：χ表示振幅；r^表示放電場(chǎng)中心，R^表示放電場(chǎng)半徑。擬合誤差定義為擬合殘差與位置野比值的平方，

MES=（∑（ETr-Wh）/∑ETr）²。（11）

學(xué)習(xí)到的位置細(xì)胞可能具有單個(gè)或多個(gè)放電位置和噪聲，須對(duì)位置細(xì)胞進(jìn)行篩選：1） 擬合誤差小于15%；2） 半徑大于5cm。

1.6空間表征均勻性度量指標(biāo)

為了表征模型提取空間特征對(duì)空間的覆蓋程度，設(shè)置了兩個(gè)度量指標(biāo)。第一個(gè)指標(biāo)是每個(gè)選取的空間位置距離其最近的位置野中心的距離為

D=min（（p-x）²+（p-y）²），（12）

式中：（p，p）表示環(huán)境中任意一點(diǎn)；（x，y）表示對(duì)應(yīng)位置最近的位置野中心。如果D存在較大的值，說(shuō)明環(huán)境中存在某些區(qū)域未被位置野覆蓋到。因此，可以通過(guò)觀察D的分布來(lái)判斷位置細(xì)胞對(duì)環(huán)境的覆蓋程度。

由于位置選取具有隨機(jī)性，所以設(shè)置第二個(gè)度量指標(biāo)，每個(gè)位置野中心與其最近的另一個(gè)位置細(xì)胞的位置野中心之間距離的最大值為

D=max（min（（x-x）²+（y-y）²）），（13）

式中：（x，y）和（x，y）分別表示兩個(gè)不同的位置野中心坐標(biāo)。如果D較小，可能是由于位置細(xì)胞聚集在一小部分區(qū)域。因此需要聯(lián)合這兩個(gè)指標(biāo)才能準(zhǔn)確地判斷位置細(xì)胞對(duì)環(huán)境的表征程度。

2分析與討論

2.1實(shí)驗(yàn)結(jié)果

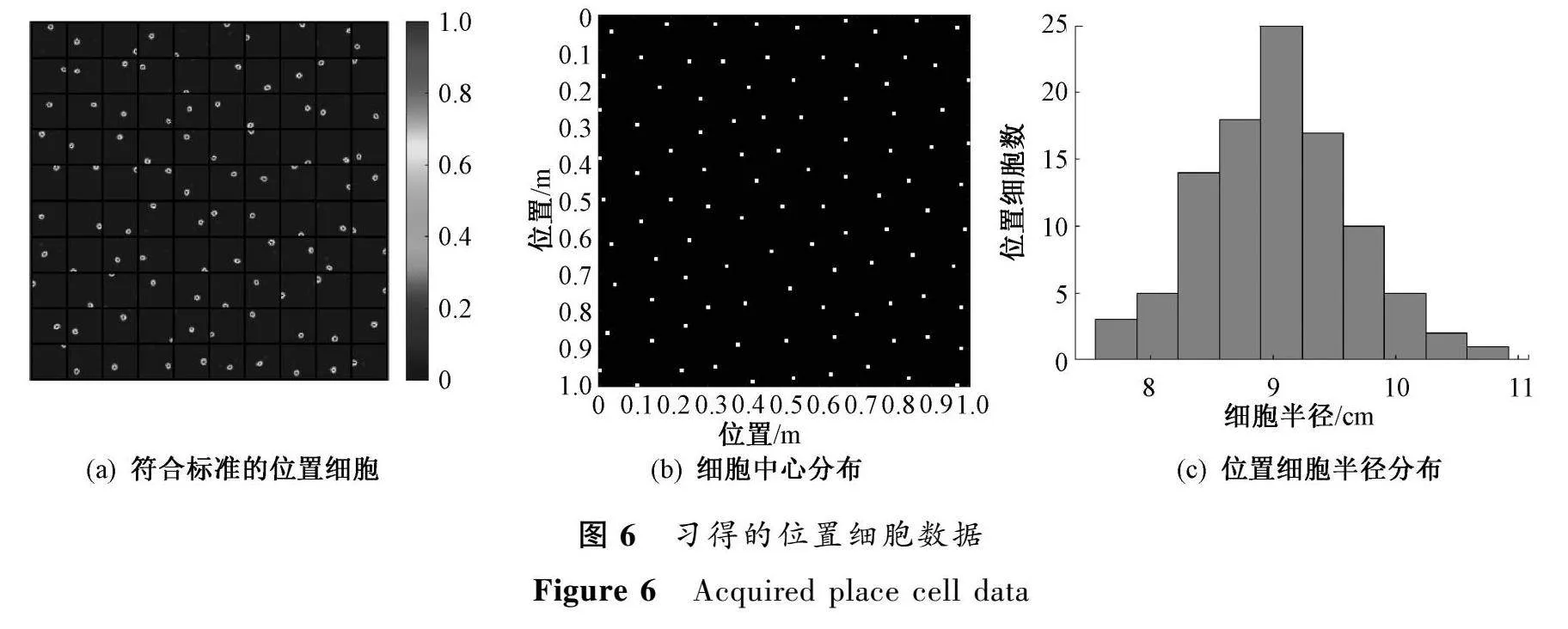
研究中，經(jīng)過(guò)3 000次的訓(xùn)練，使用多個(gè)間距和方向的柵格細(xì)胞作為內(nèi)嗅輸入，在內(nèi)嗅-海馬反饋環(huán)路模型中，使用非負(fù)稀疏編碼獲得了海馬區(qū)域的位置細(xì)胞響應(yīng)，且所有位置細(xì)胞均符合標(biāo)準(zhǔn)，如圖6（a）所示。由圖6（b）中位置細(xì)胞中心在環(huán)境中的分布可以看出，經(jīng)過(guò)反饋環(huán)路的內(nèi)嗅-海馬模型學(xué)習(xí)之后，位置細(xì)胞能夠相當(dāng)均勻地覆蓋整個(gè)環(huán)境。每個(gè)位置細(xì)胞都擁有獨(dú)特的空間選擇性放電模式，這驗(yàn)證了反饋環(huán)路網(wǎng)絡(luò)模型可以學(xué)習(xí)并生成對(duì)環(huán)境具有完整空間編碼的神經(jīng)元。

較小的位置細(xì)胞中心距離意味著更可靠和有效的學(xué)習(xí)結(jié)果，這反映了位置細(xì)胞對(duì)環(huán)境的覆蓋更為均勻。具體地，位置細(xì)胞中心距離越小，說(shuō)明環(huán)境中的每個(gè)位置都更接近某個(gè)位置細(xì)胞的中心，能夠被位置細(xì)胞很好地覆蓋。這表示位置細(xì)胞作為整體時(shí)，可以很好地對(duì)環(huán)境進(jìn)行編碼，而沒(méi)有遺漏的區(qū)域。位置細(xì)胞半徑對(duì)實(shí)驗(yàn)結(jié)果的影響主要體現(xiàn)在空間分辨率上，半徑越小，每個(gè)位置細(xì)胞的感受野越小，對(duì)空間位置的編碼就越精細(xì)，空間分辨率越高，但半徑太小會(huì)導(dǎo)致需要更多的位置細(xì)胞才能完全覆蓋環(huán)境，所以半徑大小需要達(dá)到最優(yōu)化。因此，小的位置細(xì)胞中心距離和適中的半徑大小都意味著位置細(xì)胞對(duì)空間的有效編碼，反映了模型的良好學(xué)習(xí)效果。

在構(gòu)建的內(nèi)嗅-海馬反饋循環(huán)網(wǎng)絡(luò)模型中，研究了學(xué)習(xí)到的位置細(xì)胞的位置野半徑分布情況。通過(guò)提取所有位置野數(shù)據(jù)，并用二維高斯函數(shù)進(jìn)行擬合，結(jié)果如圖6（c）所示。統(tǒng)計(jì)分析結(jié)果顯示，位置野半徑主要分布在8cm到10cm之間。這是因?yàn)椴捎玫膶W(xué)習(xí)環(huán)境為1m×1m的小環(huán)境，所以表現(xiàn)出較小的半徑值。

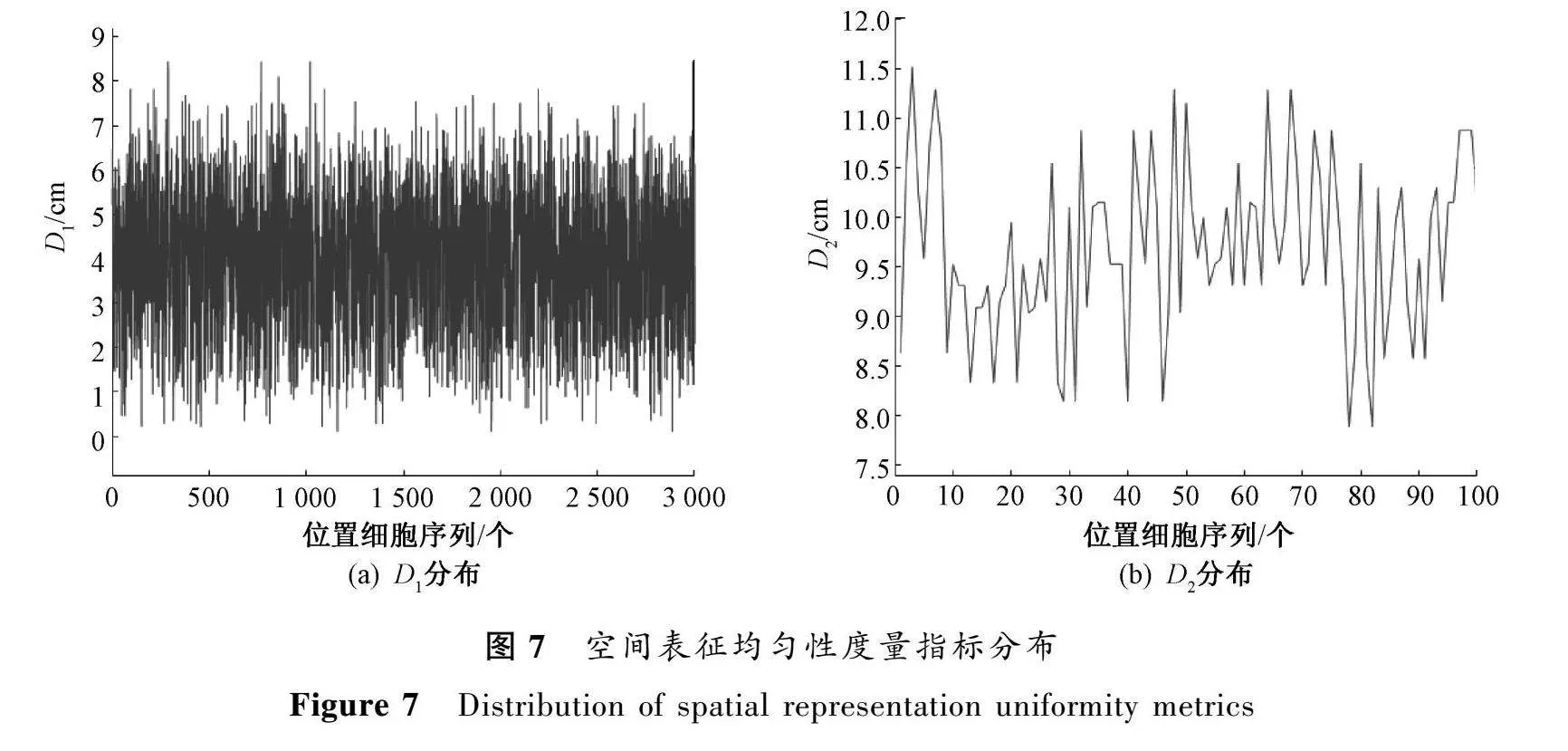
為了探究位置細(xì)胞對(duì)環(huán)境的表征程度，分別計(jì)算得到D和D的分布情況，如圖7所示。

由圖7可以看出，每個(gè)位置與其最近的細(xì)胞中心之間的距離最大值為8.45cm，平均值為4.02cm；最近的位置細(xì)胞中心之間距離的最大值為11.82cm，平均值為9.70cm。這些實(shí)驗(yàn)結(jié)果表明，通過(guò)內(nèi)嗅-海馬反饋環(huán)路學(xué)習(xí)模型學(xué)習(xí)之后，能夠生成有效表征環(huán)境的位置細(xì)胞。同時(shí)也印證了所構(gòu)建模型的可靠性和有效性。

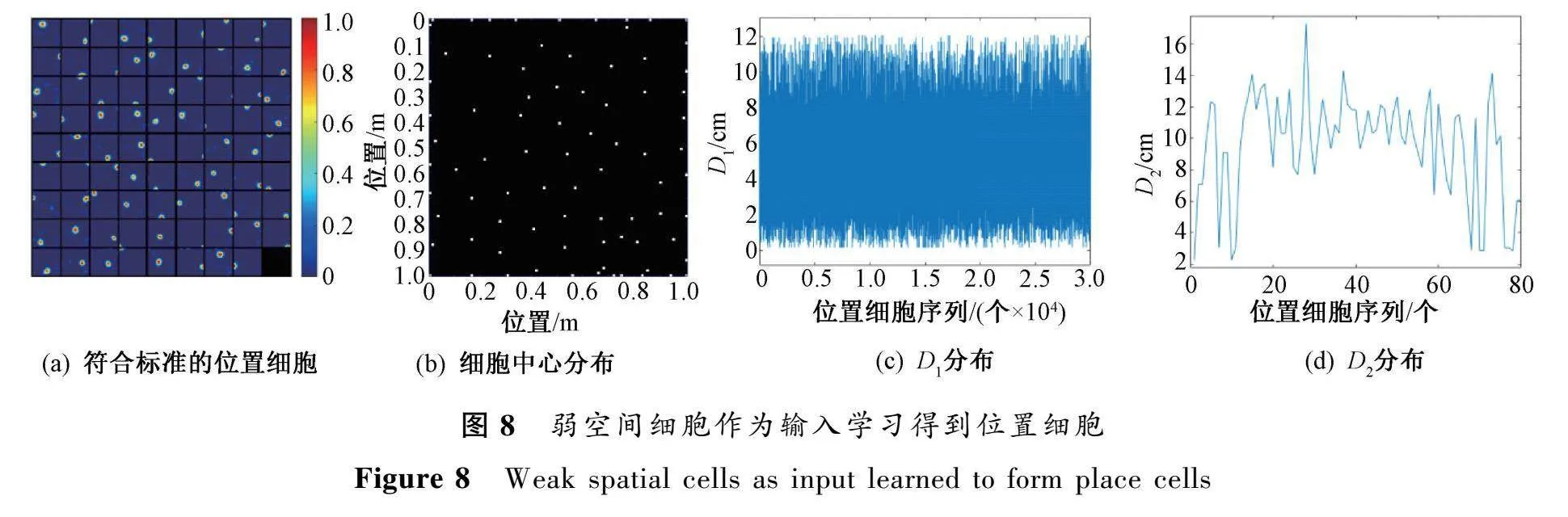
弱空間細(xì)胞的輸出是環(huán)境中每個(gè)位置對(duì)應(yīng)的激活值。當(dāng)僅使用弱空間細(xì)胞作為內(nèi)嗅輸入，研究發(fā)現(xiàn)，模型仍然能夠?qū)W習(xí)到具有單峰位置野的位置細(xì)胞，且對(duì)空間環(huán)境具有一定的表征作用，如圖8所示，分別記錄了符合標(biāo)準(zhǔn)的位置細(xì)胞、細(xì)胞中心分布以及D和D分布情況。該結(jié)果與實(shí)驗(yàn)證據(jù)一致^［20］，即由于弱空間細(xì)胞的存在，導(dǎo)致位置細(xì)胞在發(fā)育過(guò)程中早于柵格細(xì)胞出現(xiàn)。

盡管弱空間細(xì)胞的放電野與柵格細(xì)胞的周期性模式有明顯不同，但實(shí)驗(yàn)結(jié)果表明，弱空間細(xì)胞仍可為基于稀疏編碼的內(nèi)嗅-海馬回路模型提供充足的空間信息，使模型能夠準(zhǔn)確解碼內(nèi)嗅細(xì)胞的響應(yīng)并生成精確的空間表示。與僅使用柵格細(xì)胞作為內(nèi)嗅輸入相比，D和D的最大值有所增加，這是因?yàn)槿蹩臻g細(xì)胞本身所含空間信息較少，導(dǎo)致最終學(xué)習(xí)到的位置細(xì)胞數(shù)量減少。當(dāng)僅以弱空間細(xì)胞作為輸入時(shí)，學(xué)習(xí)到的位置細(xì)胞的放電野的平均值為11.87cm，標(biāo)準(zhǔn)差為1.67cm，明顯大于僅用柵格細(xì)胞輸入學(xué)習(xí)所得到的半徑。因此，盡管弱空間細(xì)胞可提供空間信息，但如果僅依賴弱空間細(xì)胞作為輸入，會(huì)降低海馬位置表示的空間分辨率。

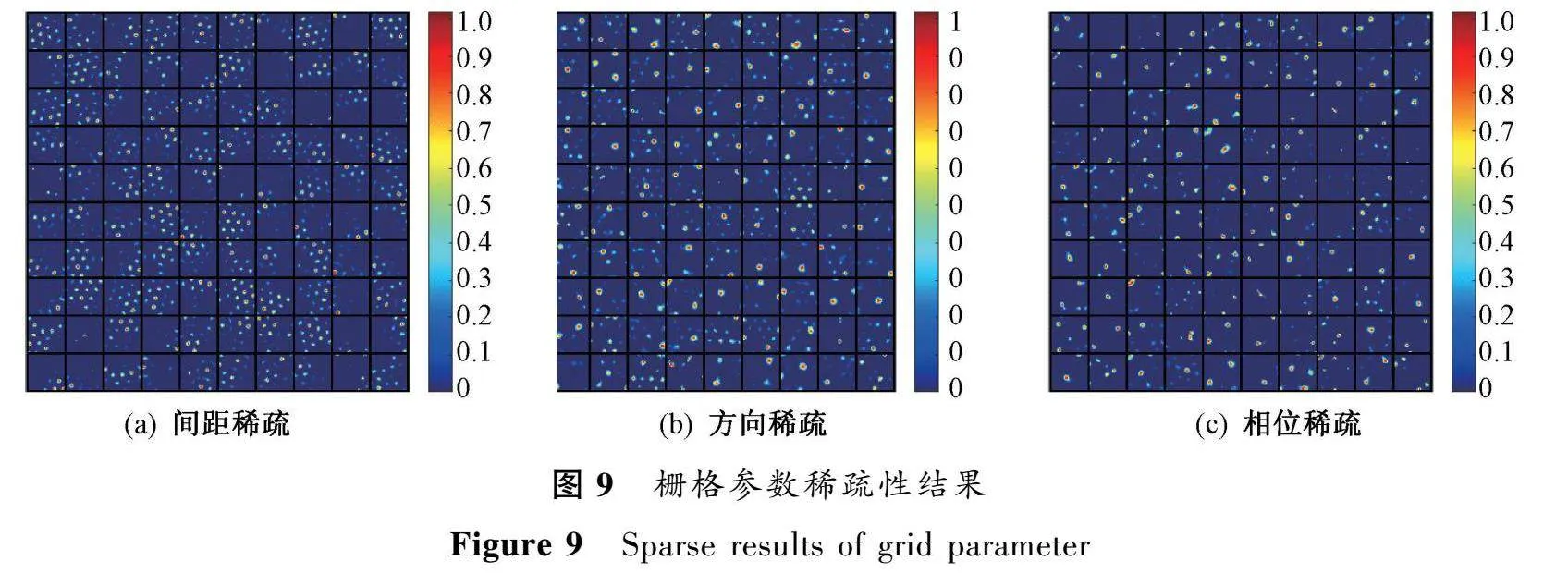
2.2柵格參數(shù)稀疏性對(duì)學(xué)習(xí)位置細(xì)胞的影響

當(dāng)輸入給海馬體的柵格細(xì)胞只有單一尺度和方向時(shí)，學(xué)習(xí)到的位置細(xì)胞會(huì)出現(xiàn)多個(gè)不連續(xù)的放電場(chǎng)。為了探究本文所提模型的可用性，單獨(dú)控制了柵格細(xì)胞的三個(gè)關(guān)鍵參數(shù)。實(shí)驗(yàn)結(jié)果如圖9所示。結(jié)果顯示，當(dāng)模型控制單一參數(shù)進(jìn)行位置細(xì)胞學(xué)習(xí)時(shí)，都產(chǎn)生了不同數(shù)量的多峰位置細(xì)胞，這是因?yàn)椋簴鸥駞?shù)的稀疏性導(dǎo)致覆蓋空間的柵格細(xì)胞不足，位置細(xì)胞難以對(duì)空間建立精確表達(dá)；柵格方向的減少會(huì)降低空間的方向信息，導(dǎo)致位置細(xì)胞對(duì)不同方向的選擇能力降低；參數(shù)稀疏會(huì)降低輸入獨(dú)特性，難以學(xué)習(xí)到獨(dú)特的位置表達(dá)。同時(shí)，柵格參數(shù)稀疏化后產(chǎn)生多峰響應(yīng)，說(shuō)明柵格結(jié)構(gòu)的完整性是實(shí)現(xiàn)單峰空間選擇性的必要條件。此外，這也可能是大腦齒狀回中多峰細(xì)胞（顆粒細(xì)胞）產(chǎn)生的原因之一。

2.3稀疏性驅(qū)動(dòng)選擇性位置野生成

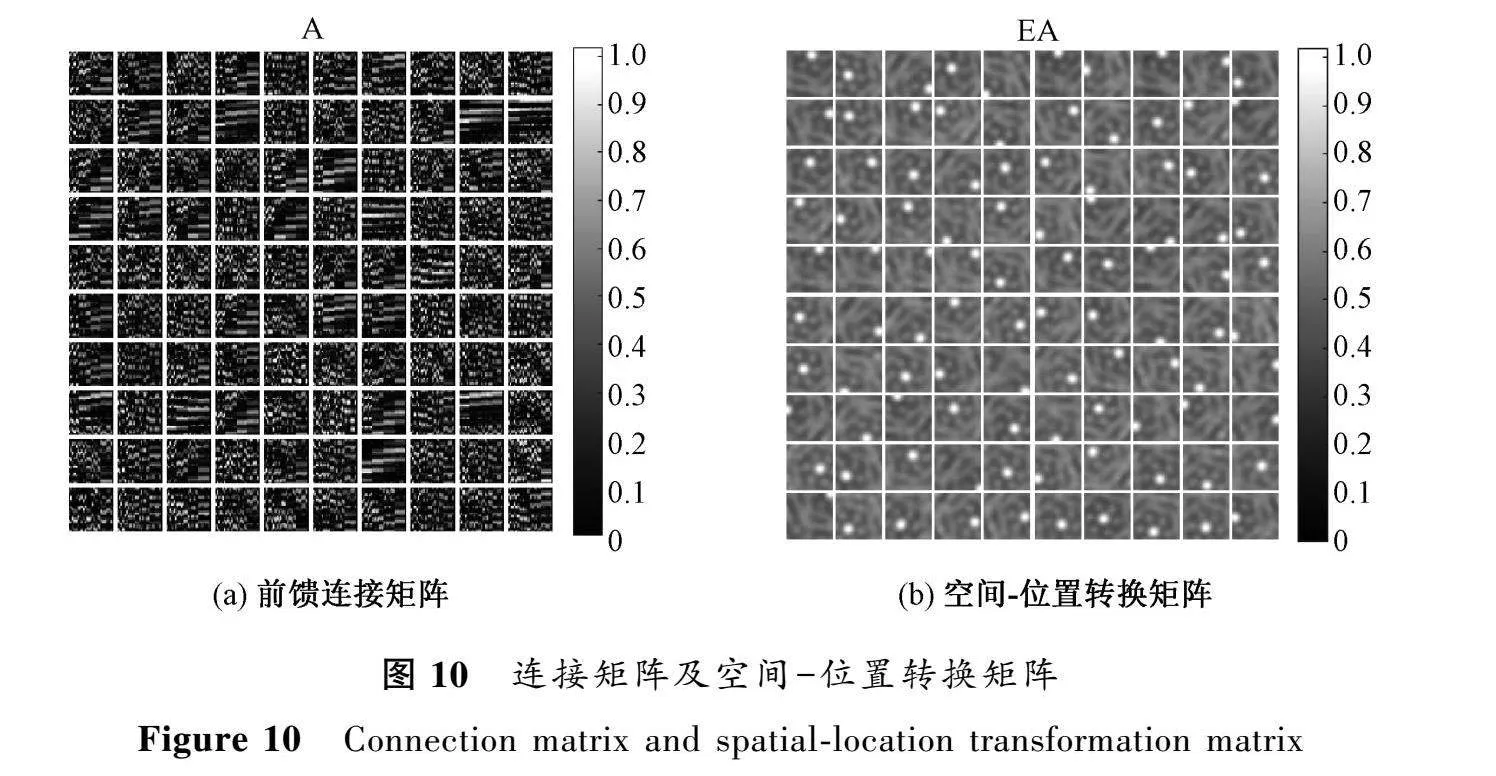
在構(gòu)建的編碼學(xué)習(xí)模型中，研究發(fā)現(xiàn)僅僅通過(guò)設(shè)定神經(jīng)元響應(yīng)的稀疏性約束就可自發(fā)地學(xué)習(xí)到空間選擇性細(xì)胞。具體來(lái)說(shuō)，每個(gè)位置細(xì)胞只選擇連接部分的特定柵格細(xì)胞，而不同位置細(xì)胞選擇的柵格細(xì)胞各不相同。這種稀疏連接方式形成了所學(xué)習(xí)的空間-位置轉(zhuǎn)換矩陣，每個(gè)位置細(xì)胞對(duì)應(yīng)矩陣中的一個(gè)空間子圖，如圖10所示。

早在1953年，研究人員發(fā)現(xiàn)同類細(xì)胞受到刺激后會(huì)抑制相鄰細(xì)胞的放電野的激活^［17］，這種抑制機(jī)制被認(rèn)為是腦區(qū)實(shí)現(xiàn)精確編碼的重要細(xì)胞機(jī)制之一。本文設(shè)計(jì)模型沒(méi)有添加額外的競(jìng)爭(zhēng)抑制機(jī)制，稀疏編碼本身實(shí)現(xiàn)了位置細(xì)胞之間的抑制作用。結(jié)果顯示，這種基于稀疏表示的學(xué)習(xí)機(jī)制可以自發(fā)產(chǎn)生單峰空間響應(yīng)模式。該結(jié)果表明，編碼稀疏性約束是生成腦區(qū)空間細(xì)胞選擇性的可能原因，為進(jìn)一步探索記憶形成和空間表示的神經(jīng)計(jì)算機(jī)制提供了重要啟發(fā)。

2.4模型魯棒性對(duì)比實(shí)驗(yàn)

在實(shí)際工作中，不可避免地存在各種噪聲，所以測(cè)試模型對(duì)不同強(qiáng)度噪聲的魯棒性非常關(guān)鍵。現(xiàn)有研究很少關(guān)注空間學(xué)習(xí)模型在噪聲環(huán)境下的表現(xiàn)。因此，本研究通過(guò)在模型的輸入部分引入不同強(qiáng)度的高斯噪聲來(lái)測(cè)試所提出模型在不同輸入噪聲條件下的魯棒性。本部分分別測(cè)試了均值為0.015、0.025和0.03，標(biāo)準(zhǔn)差均為0的高斯噪聲對(duì)學(xué)習(xí)位置細(xì)胞的影響，實(shí)驗(yàn)結(jié)果如圖11所示。

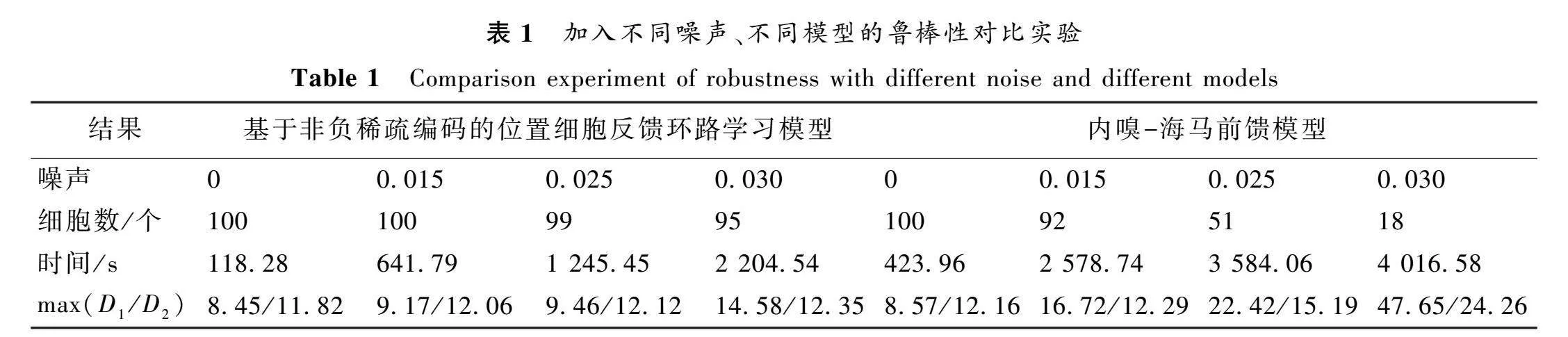
圖11中，分別顯示了細(xì)胞中心分布和符合標(biāo)準(zhǔn)的位置細(xì)胞數(shù)。結(jié)果表明，當(dāng)加入噪聲的標(biāo)準(zhǔn)差為0.015時(shí)，模型學(xué)習(xí)到的所有位置細(xì)胞仍符合標(biāo)準(zhǔn)，說(shuō)明此噪聲水平下模型未受顯著影響。隨著噪聲標(biāo)準(zhǔn)差升至0.025，學(xué)習(xí)后僅有一個(gè)位置細(xì)胞不符合標(biāo)準(zhǔn)。當(dāng)噪聲標(biāo)準(zhǔn)差達(dá)到0.030時(shí)，有五個(gè)位置細(xì)胞出現(xiàn)問(wèn)題。盡管存在個(gè)別不合格的細(xì)胞，不同水平噪聲條件下模型學(xué)習(xí)到的位置細(xì)胞整體上仍能較為均勻地表示環(huán)境空間。這說(shuō)明模型對(duì)不同強(qiáng)度的噪聲都具有較好的魯棒性。此外，與前饋模型的比較實(shí)驗(yàn)（見(jiàn)表1）也顯示，本模型對(duì)噪聲的抵抗力更強(qiáng)。

實(shí)驗(yàn)中，分別統(tǒng)計(jì)了不同噪聲強(qiáng)度對(duì)模型學(xué)習(xí)到的符合標(biāo)準(zhǔn)的位置細(xì)胞數(shù)、所需時(shí)間以及空間表征指標(biāo)D和D的最大值。實(shí)驗(yàn)結(jié)果顯示，當(dāng)不存在噪聲時(shí)，兩種模型學(xué)習(xí)到的位置細(xì)胞數(shù)沒(méi)有明顯差異，但本文所提模型所需的學(xué)習(xí)時(shí)間更短，能夠更快地提取空間信息，因此具有更高的工作效率。且隨著噪聲強(qiáng)度的增加，本文所提模型更優(yōu)于內(nèi)嗅-海馬前饋模型，主要體現(xiàn)在以下幾個(gè)方面。

首先，在各種強(qiáng)度噪聲條件下，所提模型學(xué)習(xí)到的位置細(xì)胞數(shù)均多于內(nèi)嗅-海馬前饋模型，說(shuō)明其對(duì)噪聲的抵抗力更強(qiáng)，可以在噪聲環(huán)境下依然學(xué)習(xí)到較多符合標(biāo)準(zhǔn)的位置細(xì)胞。

其次，內(nèi)嗅-海馬前饋模型的學(xué)習(xí)時(shí)間隨噪聲增強(qiáng)而快速增加，但本文所提模型學(xué)習(xí)時(shí)間增長(zhǎng)較慢。這表明反饋機(jī)制可以更高效地處理噪聲干擾。

最后，所提模型中反映空間覆蓋均勻性的D和D最大值均低于內(nèi)嗅-海馬反饋模型，且所提模型中D和D的最大值隨噪聲增加而緩慢增大。尤其在高噪聲（均值為0.03）下，內(nèi)嗅-海馬前饋模型的D和D嚴(yán)重惡化，而本文所提模型依然保持較低水平。

綜上，從學(xué)習(xí)到的位置細(xì)胞數(shù)量、學(xué)習(xí)時(shí)間和空間表征幾個(gè)方面綜合比較，充分證明了本文所提模型比海馬-內(nèi)嗅前饋模型對(duì)不同強(qiáng)度的噪聲具有更強(qiáng)的魯棒性。這驗(yàn)證了反饋機(jī)制在提高模型抗干擾能力方面的優(yōu)勢(shì)。反饋連接廣泛存在于海馬回路中，海馬回路的反饋調(diào)節(jié)在處理環(huán)境變化方面起重要作用。本研究表明，所提模型不僅有利于空間學(xué)習(xí)，也使學(xué)習(xí)到的空間表示對(duì)噪聲更有魯棒性，這為理解反饋機(jī)制在海馬回路處理環(huán)境變化中的生理學(xué)作用提供了計(jì)算模型證據(jù)。

3結(jié)論

本文提出的基于非負(fù)稀疏編碼的位置細(xì)胞反饋環(huán)路學(xué)習(xí)模型，能夠快速捕捉空間信息，并高效學(xué)習(xí)得到位置細(xì)胞，均勻地表征空間環(huán)境。當(dāng)僅有弱空間細(xì)胞作為內(nèi)嗅皮層的輸入時(shí)，所提模型能夠很好地發(fā)揮作用，學(xué)習(xí)到足夠的位置細(xì)胞來(lái)充分地表征空間位置。通過(guò)控制輸入柵格細(xì)胞模型參數(shù)的稀疏性，能夠得到類似于齒狀回中的顆粒細(xì)胞，具有多個(gè)不規(guī)則的放電野。對(duì)比實(shí)驗(yàn)結(jié)果顯示，所提模型具有更強(qiáng)的抗干擾能力，在學(xué)習(xí)得到位置細(xì)胞表征環(huán)境空間特征方面具有更高的效率。

參考文獻(xiàn)：

［1］AERY JONES E A， GIOCOMO L M. Neural ensembles in navigation： from single cells to population codes［J］. Current opinion in neurobiology， 2023， 78： 102665.

［2］ORMOND J， O′KEEFE J. Hippocampal place cells have goal-oriented vector fields during navigation［J］. Nature， 2022， 607（7920）： 741-746.

［3］ZHANG X M， SCHLGL A， JONAS P. Selective routing of spatial information flow from input to output in hippocampal granule cells［J］. Neuron， 2020， 107（6）： 1212-1225.

［4］SORSCHER B， MEL G C， OCKO S A， et al. A unified theory for the computational and mechanistic origins of grid cells［J］. Neuron， 2023， 111（1）： 121-137.

［5］LIAN Y B， BURKITT A N. Learning spatiotemporal properties of hippocampal place cells［J］. eNeuro， 2022， 9（4）： ENEURO.0519-ENEURO.0521.

［6］WANG J R. The interplay between grid and place cell networks and contextual inputs［C］∥2022 2nd International Conference on Bioinformatics and Intelligent Computing. New York：ACM Press， 2022：247-252.

［7］SOTO F A， NARASIWODEYAR S. Improving the validity of neuro imaging decoding tests of invariant and configural neural representation［J］. PLoS computational biology， 2023， 19（1）： e1010819.

［8］VAFIDIS P， OWALD D， D′ALBIS T， et al. Learning accurate path integration in ring attractor models of the head direction system［J］. eLife， 2022， 11： e69841.

［9］LIU Z W， WAN G C， PRAKASH B A， et al. A review of graph neural networks in epidemic modeling［EB/OL］.（2024-03-28）［2024-05-10］.https：∥arxiv.org/pdf/2403.19852v3.

［10］FANG M Y S， MUDIGONDA M， ZARCONE R， et al. Learning and inference in sparse coding models with Langevin dynamics［J］. Neural computation， 2022， 34（8）： 1676-1700.

［11］SRINIVASAN S， DASTE S， MODI M N， et al. Effects of stochastic coding on olfactory discrimination in flies and mice［J］. PLoS biology， 2023， 21（10）： e3002206.

［12］孟志林， 趙冬曄， 斯白露， 等. 基于哺乳動(dòng)物空間認(rèn)知機(jī)制的機(jī)器人導(dǎo)航綜述［J］. 機(jī)器人， 2023， 45（4）： 496-512.

MENG Z L， ZHAO D Y， SI B L， et al. A survey on robot navigation based on mammalian spatial cognition［J］. Robot， 2023， 45（4）： 496-512.

［13］CHEN Z Q， NASRALLAH A， ALEMOHAMMAD M， et al. Neuromorphic model of hippocampus place cells using an oscillatory interference technique for hardware implementation［J］. Neuromorphic computing and engineering， 2022， 2（4）： 044013.

［14］TRAUB R D， WHITTINGTON M A， CUNNINGHAM M O. Simulation of oscillatory dynamics induced by an approximation of grid cell output［J］. Reviews in the neurosciences， 2022， 34（5）： 517-532.

［15］HUANG X J， SONG Z G， XU J. Amplitude death， oscillation death， and stable coexistence in a pair of VDP oscillators with direct-indirect coupling［J］. Electronic research archive， 2023， 31（11）： 6964-6981.

［16］GARDNER R J， HERMANSEN E， PACHITARIU M， et al. Toroidal topology of population activity in grid cells［J］. Nature， 2022， 602（7895）： 123-128.

［17］BHASIN G， NAIR I R. Dynamic hippocampal CA2 responses to contextual spatial novelty［J］. Frontiers in systems neuroscience， 2022， 16： 923911.

［18］LUTHER K， SEUNG H S. Sensitivity of sparse codes to image distortions［J］. Neural computation， 2022， 34（7）： 1616-1635.

［19］NARDIN M， CSICSVARI J， TKAACˇG1IK G， et al. The structure of hippocampal CA1 interactions optimizes spatial coding across experience［J］. The journal of neuroscience， 2023， 43（48）： 8140-8156.

［20］ULSAKER-JANKE I， WAAGA T， WAAGA T， et al. Grid cells in rats deprived of geometric experience during development［J］. Proceedings of the national academy of sciences of the United States of America， 2023， 120（41）： e2310820120.