量子核判別分析算法

摘要： 核判別分析法通過核函數擴展了線性判別分析對非線性數據的處理能力，成為模式識別領域中一個重要的分支。然而，隨著數據的指數增長，經典核判別分析算法在提取特征時會消耗大量計算資源。針對這一問題，利用量子疊加性和并行性提出了一種量子核判別分析算法。首先，借助量子隨機存儲器技術與控制旋轉操作構造需要的類間矩陣和類內矩陣所對應的密度算子；然后，融入線性方程的求解思路并行獲取特征態。理論分析表明，所提算法與經典算法相比具有指數級加速。

關鍵詞： 量子機器學習； 非線性判別分析； 核函數； 特征提取； 量子厄米特鏈積； 相位估計

中圖分類號： TP3

文獻標志碼： A

文章編號： 1671-6841（2025）01-0061-06

DOI： 10.13705/j.issn.1671-6841.2023146

Quantum Kernel Discriminant Analysis Algorithm

KANG Rongcheng^1，2， YU Kai^1，2， ZHANG Xin³， LIN Song¹， GUO Gongde¹

（1.College of Computer and Cyber Security， Fujian Normal University， Fuzhou 350117， China;

2.Digital Fujian Environmental Monitoring Internet of Things Laboratory， Fujian Normal University， Fuzhou

350117， China; 3.College of Mathematics and Statistics， Fujian Normal University， Fuzhou 350117， China）

Abstract： Kernel discriminant analysis was an important branch in the field of pattern recognition which aimed to expand the ability of linear discriminant analysis to process nonlinear data by kernel function. However， with the exponential growth of data， the classical kernel discriminant analysis algorithm consumed a lot of computing resources in extracting features. To solve this problem， a quantum kernel discriminant analysis algorithm was proposed based on quantum superposition and parallelism. Firstly， the density operators corresponding to the desired between-class scatter matrix and within-class scatter matrix were constructed with quantum random access memory technology and controlled rotation operation. Then， the eigenstates were obtained in parallel by incorporating the solution idea of linear equation. Theoretical analysis showed that the algorithm could achieve exponential acceleration compared with the classical algorithm.

Key words： quantum machine learning; nonlinear discriminant analysis; kernel function; feature extraction; quantum hermitian chain product; phase estimation

0引言

線性判別分析是機器學習中常用的科學手段，然而在許多現實應用中，如人臉識別^［1］中涉及光照、角度等諸多因素時，線性方法不能完成任務，需非線性方法進一步處理與分析。核判別分析（kernel discriminant analysis，KDA）是非線性領域重要的算法之一，在數據降維和判別分類方面都有著廣泛應用。它利用核函數思想將線性判別分析（linear discriminant analysis，LDA）從線性領域擴展到非線性領域。這樣，KDA保持了線性判別分析能夠最大化蘊含分類信息的特征，克服了非線性數據降維后不同類別數據可能重疊的難題。然而，經典的核判別分析在提取特征（投影空間方向）時需要強大的計算力。特別是在大數據時代，經典核判別分析容易陷入計算困境。

量子機器學習是一種利用量子計算特性進一步優化傳統機器學習的新興研究方向。用于求解線性方程的Harrow-Hassidim-Lloyd（HHL）算法與經典算法相比實現了指數加速。在此基礎上，研究者們提出了解決模式分類和回歸模型等問題的量子算法^［2-6］，并提出了將量子計算與人工神經網絡相結合的量子神經網絡算法^［7-12］。作為機器學習的重要領域，數據降維^［13］在大數據時代顯得尤為重要，一些學者融入量子計算技術對此進行了探索。針對線性判別分析，Cong等^［14］利用量子模擬和厄米特鏈積技術相對于經典算法可以實現指數級加速的優點，提取一組可以獲得最優投影方向的量子態。Yu等^［15］利用線性組合避免了類間矩陣不可逆的影響，并以量子態的形式輸出降維數據，實現了平方級加速。

鑒于上述量子機器算法在計算速度上的優越性，本文對核判別分析算法進行了研究，提出一種量子核判別分析（quantum kernel discriminant analysis，QKDA）算法。所提算法主要基于相位估計和厄米特鏈積技術，并融入HHL求解思路獲得投影空間的特征向量。提取了主特征后就可以對原數據進行投影降維和對新數據進行分類，并且成本很低。與此同時，我們也給出了相應的電路圖。通過理論分析表明，本文算法相比于經典算法實現了指數加速。

1預備知識

1.1經典的核判別分析算法

核判別分析是一種利用核函數思想將線性判別分析擴展到非線性領域的分析方法。它既保持了線性判別分析能夠最大化蘊含分類信息的特征，又能對非線性數據進行處理。經典的核判別分析算法旨在返回最大化類間方差，最小化類內方差的投影特征方向。

考慮一個包含C種類別的數據集X=｛X，X，…，X｝，其中X（c=1，2，…，C）為每種類別的樣本集合。N為屬于類別c的樣本數，即N=∑Cc=1N。設樣本X∈R^D（i=1，2，…，N）映射到高維特征空間R～后為Φ（x），即x→Φ（x）∈R～，則在特征空間中的類內散度矩陣和類間散度矩陣分別為

S^Φ=∑Cc=1∑Nj=1［Φ（x^c）-μ^Φ］［Φ（x^c）-μ^Φ］^T，

S^Φ=∑Cc=1（μ^Φ-μ^Φ）（μ^Φ-μ^Φ）^T，

其中：μ^Φ=1N∑Nj=1Φ（x^c）為特征空間R～中第c類樣本的均值；μ^Φ=1N∑Ni=1Φ（x）為總的樣本均值；x^c為第c類樣本中的第j個樣本。設投影矩陣w=［w，w，…，w］（1≤d≤C-1），其中w（i=1，2，…，d）為N×1的列向量，則核判別分析的優化目標為maxJ（w）=（w^TS^Φw）/（w^TS^Φw）。其中特征向量w可由Φ（x），Φ（x），…，Φ（x）線性表示出，即w=∑Nj=1αΦ（x），系數矩陣為α=［α，α，…，α］。則優化問題可以轉化為

maxJ（α）=（α^TM～α）/（α^TN～α），（1）

M～=∑Cc=1（M-M）（M-M）^T，（2）

N～=∑Cc=1K（I-1）KT，（3）

其中：（M）=1N∑Nj=1K（x，x^c）（i=1，2，…，N）表示向量M的第i個分量;向量M的第i個分量為（M）=1N∑Nj=1K（x，x^c）（i=1，2，…，N）;K為N×N階矩陣，（K）=K（x，x^c）表示矩陣K第m行第n列的元素；I為N階單位矩陣；1為元素均為1/N的N階方陣。即將原本求解w∈R～的目標轉化為求解α∈R～。可以通過求解N～^－1M～矩陣的特征向量獲得。

1.2量子厄米特鏈積算法

量子厄米特鏈積是構造厄米矩陣連乘積相對應的密度矩陣的算法。它可以有效地實現k個標準N×N的厄米半正定矩陣連乘積［f（A）…f（A）］·［f（A）…f（A）］的密度算子形式，其中f，…，f是有泰勒級數收斂的函數，符號“”為共軛轉置。該過程的實現可以看作是量子求解線性方程（HHL算法），即實現矩陣運算x=A^-1b。因此，量子厄米特鏈積實現的一般步驟描述如下。

Step 1首先，初始化狀態ψ〉〈ψρ，ψ〉=∑T－1τ=0π（τ+1/2）Tτ〉，可以看作HHL算法的初始狀態，ρ=1N∑Ni=1i〉〈i可以看作是算法中的b〉，其中i〉為計算基。

Step 2矩陣A的特征向量表示為｛u〉｝^N，令｛λ〉｝^N為對應的特征值。然后在特征向量基｛u〉｝^N上對ρ進行分解，可以得到ρ=∑Nl，l′=1βu〉〈u，此處β表示ρ在該特征向量基下的系數。

Step 3先利用矩陣求冪技術在O（Xκ²/ε³）時間內獲得厄米算子A的指數化形式e^iAt，其中：O（X）為構造A的時間；t=O（κ/ε）；κ是矩陣的條件數（最大特征值與最小特征值的比值）；ε為容忍誤差。然后利用e^iAt作為受控酉算子在ρ上執行相位估計可得

ρ′=∑Nl，l′=1βλ〉〈λ×u〉〈u。

Step 4增加輔助寄存器處于狀態0〉〈0，并由λ〉〈λ寄存器分別控制，實現旋轉

ψ〉=1－G²f（λ）²0〉+Gf（λ）1〉。

不失一般性， G是一個階為O（min｛f（λ）^-1｝）的常數。有效執行該旋轉后，整個系統的狀態為

ρ″=∑Nl，l′=1βλ〉〈λu〉〈uψ〉〈ψ。

Step 5執行Step 3的逆操作，即逆相位估計，并丟棄存放特征值的寄存器，此時狀態為

ρ=∑Nl，l′=1βu〉〈uψ〉〈ψ。

Step 6在輔助量子比特上執行量子測量操作，獲得1〉〈1時，選擇合適的G，系統狀態為

ρ=∑Nl，l′=1ββf（λ）u〉〈uf（λ）=

f（A）I（f（A））。

利用幅度放大技術，可以在O（Xε³κ²maxf（λ）minf（λ））成功概率內完成這個步驟。進一步，用A作為矩陣， f作為函數，初態由ρ替換ρ，每次迭代j時，在ρ上使用A和f，重復上述步驟，直至獲得厄米半正定矩陣連乘積的密度算子形式。

2量子的核判別分析算法

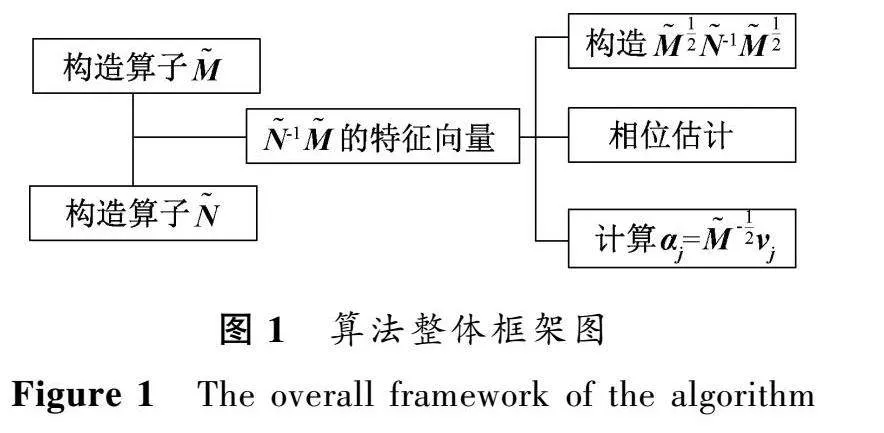
在本節中，我們設計了一個核判別分析算法的量子版本。算法的主要步驟如下：首先，構造算子M～和N～的量子形式；然后利用厄米特鏈積和相位估計求解特征值及其相應的特征向量；最終對投影向量提取所要求的主特征向量。算法的整體框架如圖1所示。

2.1制備階段

2.1.1構造算子M～

在我們的算法中，假設可以在量子隨機存取存儲器（quantum random access memory， QRAM）中通過量子訪問訓練向量數據^［16-17］。考慮具有N個樣本、C個類別的樣本集X=｛X，X，…，X｝，X（c=1，2，…，C）為樣本子集，每個樣本子集有N個D維樣本，即N=∑Cc=1N。

Step 1根據式（2）的計算，假設存在以下量子黑盒，

O（c〉i〉j〉0〉0〉）→

c〉i〉j〉‖K（x，x^c）‖〉K（x，x^c）〉，

假設K（x，x^c）〉已歸一化， O允許我們構造狀態

Ψ〉=O（1N∑Nj=1c〉i〉j〉0〉0〉）=

1N∑Nj=1c〉i〉j〉‖K（x，x^c）‖〉K（x，x^c）〉，

Ψ〉=O（1N∑Nj=1c〉i〉j〉0〉0〉）=

1N∑Nj=1c〉i〉j〉‖K（x，x^c）‖〉K（x，x^c）〉。

Step 2?;如果向量的范數形成了一個有效的可積分布，我們可以得到狀態

M〉=1N‖K（x，x^c）‖∑Nj=1c〉i〉j〉

‖K（x，x^c）‖〉K（x，x^c）〉，

M〉=1N‖K（x，x^c）‖∑Nj=1c〉i〉j〉

‖K（x，x^c）‖〉K（x，x^c）〉。

Step 3我們在M〉和M〉相對應的組件上應用減法器得到差分量M-M〉。在此基礎上，構造與M～成比例的密度矩陣

Ψ〉=N∑Cc=1c〉‖M-M‖〉M-M〉。

同樣，若向量的范數形成了一個有效的可積分布，我們可以得到狀態

Ψ〉=NA∑Cc=1‖M-M‖c〉‖M-M‖〉

M-M〉，

其中：A=∑Cc=1‖M-M‖²。

Step 4現在對Ψ〉中的第1個寄存器求偏跡，則第2個寄存器的密度矩陣為

M～〉=NA∑Cc=1‖M-M‖²M-M〉〈M-M。

由此，我們可以在時間O（log（ND））內構造厄米特算子M～。

2.1.2構造算子N～

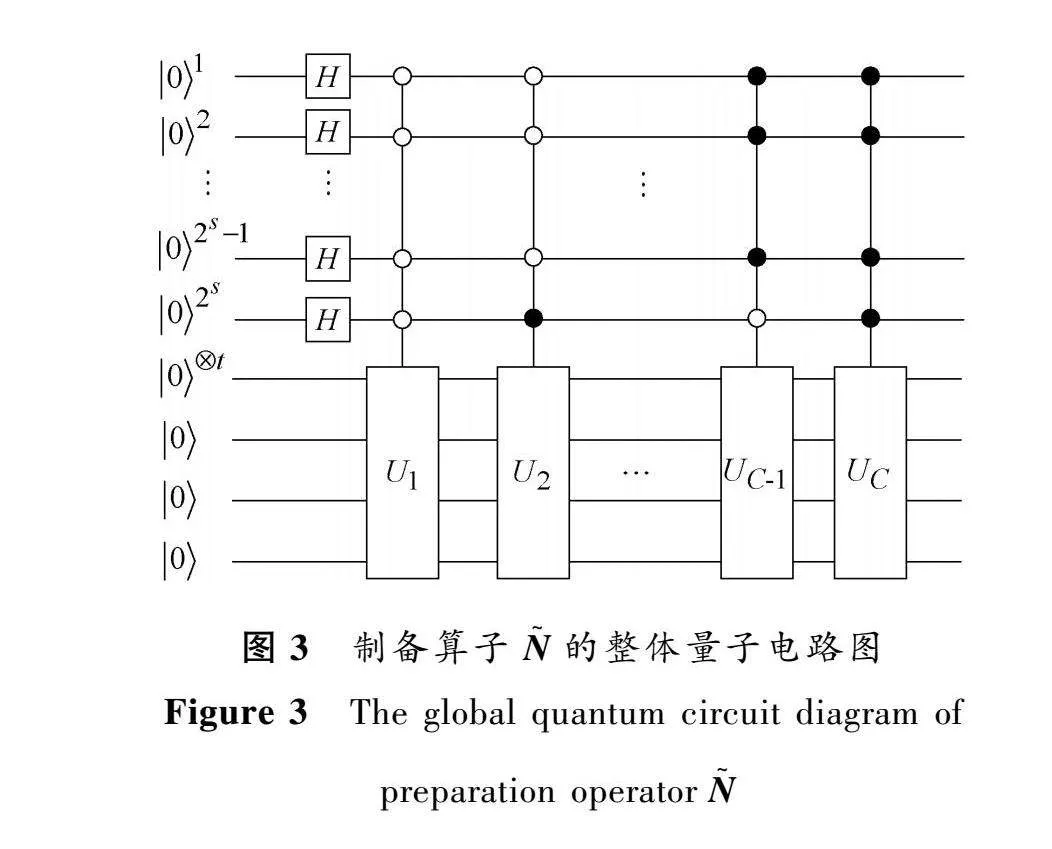
在量子形式下，可以將N～表示為矩陣的外積形式。制備算子N～的總體過程包含以下步驟。

Step 1初始化。準備初始量子態

φ⁰〉=0〉^s0〉^t0〉0〉0〉，

其中：s=logC；t=logN。

Step 2Hadamard操作。對量子態φ⁰〉的第一個寄存器執行H^s門操作，得到

φ¹〉=1C∑Cc=1c〉0〉0〉0〉0〉。

Step 3受控制備。將存儲t=logN個量子比特的第2個寄存器制備成均勻疊加態，即

0〉^t→1N∑Ni=1i〉。

設計一個酉操作U（c=1，2，…，C，表示類別），在寄存器2的控制下作用于寄存器3，可以實現

∑Ni=1i〉0〉IU1N∑Ni=1i〉1C∑Nj=1K（x，x^c）j〉，

其電路圖如圖2所示，由此我們可以得到狀態

φ²〉=1CN∑Cc=1c〉∑Ni=1i〉∑Nj=11CK（x，x^c）j〉0〉0〉，

其中：K（x，x^c）為兩個映射數據Φ（x）與Φ（x）點積的核函數值；C為歸一化常數，C=1/（‖K（x，x^c）‖）。

Step 4相位估計。利用哈密頓模擬技術獲得e^iFt，并將其作為受控酉算子，以φ²〉作為輸入執行相位估計，可以獲得

φ³〉=1CN∑Cc=1c〉∑Ni=1i〉∑Nj=11CK（x，x^c）

∑Np=1〈vj〉v〉λ〉0〉，

其中：λ為矩陣F的特征值；v為與特征值λ相應的特征向量。

Step 5受控旋轉。由寄存器4控制從狀態0〉旋轉為狀態rλ0〉+1-r²λ1〉，此時，系統的狀態變為

φ⁴〉=1CN∑Cc=10〉∑Ni=1i〉∑Nj=11CK（x，x^c）

∑Np=1〈vj〉v〉λ〉（rλ0〉+

1-r²λ1〉），

其中：r=O（minλ）為矩陣F的最小特征值。

Step 6對寄存器4執行逆相位估計，則整個系統狀態為

φ⁵〉=1CN∑Cc=10〉∑Ni=1i〉∑Nj=11CK（x，x^c）

∑Np=1〈vj〉v〉（rλ0〉+1-r²λ1〉）。

Step 7對第5個寄存器執行投影測量，執行酉操作I^tII0〉〈0，將量子態投影到0〉上，則剩下的量子系統狀態處于

φ⁶〉=1CN1N∑Cc=10〉∑Ni=1i〉

∑Nj=11CK（x，x^c）∑Np=1〈vj〉v〉rλ。

Step 8對寄存器1和3求偏跡，取跡之后得到N～的密度算子為

1CNN∑Ni，i′=1i〉〈i′∑Nj，j′=11C²K（x，x^c）K（x，x^c）

∑Np=1〈vj〉〈j′v〉r²λ。

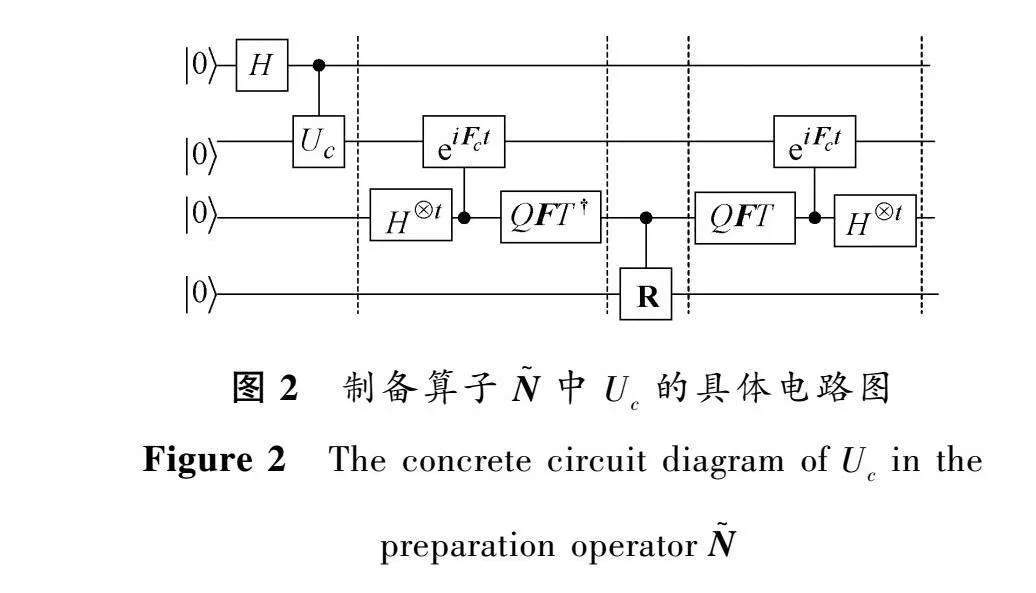
獲得N～過程的電路圖，如圖3所示。

2.2提取階段

根據經典核判別分析的知識，QKDA需要提取特征作為投影方向。本節將利用厄米鏈積技術、相位估計等技術完成投影向量的提取。

Step 1構建M～¹²N～^－1M～¹²。令α=M～^－12v，則公式（1）所表示的特征向量問題轉化為求解下面的特征值問題，

M～¹²N～^－1M～¹²v=λv，

其中：λ為M～¹²N～^－1M～¹²的特征值；v為與它對應的特征向量。對M～和N～應用實現厄米矩陣連乘積的方法在時間O（log（NN）k^3.5/ε³）內構造密度算子，

ρ=∑Dj=1λv〉〈v，

其中：λ與v分別為M～¹²N～^－1M～¹²的特征值和對應的特征向量；為了避免極小特征值情況下的指數復雜度，預先定義一個有效條件數k，并只考慮［1/k，1］范圍內的特征值來進行相位估計。

Step 2通過矩陣指數技術，可以得到e^-iρt，并且將它作為受控酉門對ρ進行量子相位估計來得到狀態的近似，

ρ′=∑jλv〉〈vλ〉〈λ，

測量λ〉系統O（d）次，以較大的概率測得d個最大的特征值，并獲得對應的主特征向量v。

3 計算α=M～^－12v。測得前d個特征值，以ρ′作為輸入，將e^-iM～-12t作為受控酉操作對ρ′進行相位估計得到狀態

∑jξ〈uv〉u〉ξ〉，

然后執行逆相位估計，可以得到

α〉=∑jξ〈uv〉u〉。

這樣就提取了主特征向量，可以借助這些特征完成對原始數據的投影，并對新數據進行投影分類。

3算法的復雜度分析

本節中，我們將對所提算法的時間復雜度進行分析。

在量子態制備階段，首先，利用量子隨機存儲器，我們在時間O（log（ND））內完成了對算子M～的制備。在制備算子N～的過程中，完成受控制備需要的時間復雜度為O（log（NN）），執行相位估計需要O（1/ε），得到相應的特征值和特征向量之后進行受控旋轉，其時間復雜度為O（1/ε），因此矩陣N～的制備總時間復雜度為O（log（NN）/ε²）。

特征向量的提取階段，在時間O（log（NN）k^3.5/ε³）內利用厄米特鏈積方法構建M～¹²N～^－1M～¹²的密度算子，通過矩陣指數技術得到相應的酉算子后作相位估計，找到M～¹²N～^－1M～¹²的主特征向量的時間復雜度為O（log（NN）/ε³），最后提取N～^－1M～的一個特征向量所需的時間復雜度為O（log（NN）k³/ε³），則提取前d個特征向量對應的時間復雜度為O（dlog（NN）k³/ε³）。

綜上可知，本文算法的總時間復雜度為O（d（log（ND）+log（NN）k^3.5/ε³））。在經典的核判別分析算法中，對于N個樣本和D維特征的數據集，計算這兩個散度矩陣的時間復雜度為O（ND）。求解廣義特征值問題的時間復雜度取決于散度矩陣的維度。假設散度矩陣的維度為m，通常情況下m≤min（N，D），求解廣義特征值問題的時間復雜度為O（m³）。通過對比可以發現，本文算法比對應的經典算法實現了指數加速。

4討論與總結

基于量子力學特性，本文提出了一種量子核判別分析算法，并給出了具體的電路圖。在數據量化階段，利用量子隨機存取存儲器和控制旋轉技術構造了相應的密度算子。然后，在求解線性方程思想的基礎上并行地得到了量子態。最后，通過測量和采樣得到了前d個特征值對應的特征向量，完成了特征提取。理論分析表明，本文算法與經典算法相比實現了指數加速。此外，本文算法可以作為一個子程序來構建更復雜的量子算法。

本文的主要創新之處在于針對經典核判別分析算法的問題提出了量子解決方案，這里借助厄米特鏈積、相位估計等現有相關技術和方法完成特征映射，降低所提量子算法的時間復雜度。然而，本文尚存在不足之處，主要在于缺少對算法的實驗論證。因為量子算法一般涉及一定量的量子比特完成控制和精度計算，然而現有的量子平臺只適合實現少量比特的算法模擬。因此，在現有技術下實現本文所提算法是有一定難度的，這也是目前大多數量子算法面臨的公共難題。如何利用少量量子比特完成同精度的計算，并且在現有量子平臺上進行實驗是我們接下來研究的重點。

參考文獻：

［1］袁欣瑞， 王海榮， 王振旭. 基于人臉識別和姿態估計的智能監考模型設計與應用［J］. 鄭州大學學報（理學版）， 2023， 55（3）： 41-49.

YUAN X R， WANG H R， WANG Z X. Design of intelligent invigilation model based on face recognition and pose estimation［J］. Journal of Zhengzhou university （natural science edition）， 2023， 55（3）： 41-49.

［2］XU L， ZHANG X Y， LIANG J M， et al. Variational quantum support vector machine based on Hadamard test［J］. Communications in theoretical physics， 2022， 74（5）： 055106.

［3］ZHANG R， WANG J， JIANG N， et al. Quantum support vector machine based on regularized Newton method［J］. Neural networks， 2022， 151： 376-384.

［4］ZHANG R， WANG J， JIANG N， et al. Quantum support vector machine without iteration［J］. Information sciences， 2023， 635： 25-41.

［5］KANEKO K， MIYAMOTO K， TAKEDA N， et al. Linear regression by quantum amplitude estimation and its extension to convex optimization［J］. Physical review A， 2021， 104（2）： 022430.

［6］CHEN M H， YU C H， GAO J L， et al. Quantum algorithm for Gaussian process regression［J］. Physical review A， 2022， 106： 012406.

［7］WEI S J， CHEN Y H， ZHOU Z R， et al. A quantum convolutional neural network on NISQ devices［J］. AAPPS bulletin， 2022， 32（1）： 1-11.

［8］LI Y C， ZHOU R G， XU R Q， et al. A quantum deep convolutional neural network for image recognition［J］. Quantum science and technology， 2020， 5（4）： 044003.

［9］MELKO R G， CARLEO G， CARRASQUILLA J， et al. Restricted Boltzmann machines in quantum physics［J］. Nature physics， 2019， 15（9）： 887-892.

［10］SHAO C P. Data classification by quantum radial-basis-function networks［J］. Physical review A， 2020， 102（4）： 042418.

［11］BEER K， BONDARENKO D， FARRELLY T， et al. Training deep quantum neural networks［J］. Nature communications， 2020， 11： 808.

［12］ALRIKABI H T S， ALJAZAERY I A， QATEEF J S， et al. Face patterns analysis and recognition system based on quantum neural network QNN［J］. International journal of interactivemobile technologies （iJIM）， 2022， 16（8）： 34-48.

［13］劉振鵬， 陳杰， 王仕磊， 等. 基于聚類和壓縮感知的高維數據發布算法［J］. 鄭州大學學報（理學版）， 2023， 55（2）： 63-69.

LIU Z P， CHEN J， WANG S L， et al. High dimensional data publishing algorithm based on clustering and compressed sensing［J］. Journal of Zhengzhou university （natural science edition）， 2023， 55（2）： 63-69.

［14］CONG I， DUAN L M. Quantum discriminant analysis for dimensionality reduction and classification［J］. New journal of physics， 2016， 18（7）： 073011.

［15］YU K， LIN S， GUO G D. Quantum dimensionality reduction by linear discriminant analysis［J］. Physica A： statistical mechanics and its applications， 2023， 614： 128554.

［16］PARK D K， PETRUCCIONE F， RHEE J KK. Circuit-based quantum random access memory for classical data［J］. Scientific reports， 2019， 9： 3949.

［17］ASAKA R， SAKAI K， YAHAGI R. Quantum random access memory via quantum walk［J］. Quantum science and technology， 2021， 6（3）： 035004.