基于GA優化神經網絡的變剛度復合材料板簧剛強度預測研究

關鍵詞：SMA驅動器;空間布置參數;BP神經網絡;遺傳算法;尋優效率

0 引言（Introduction）

為順應汽車低碳、輕量化[1]及智能化[2]的發展趨勢，將具有形狀記憶特性的鎳鈦合金絲（SMA）植入三維編織體中形成SMA驅動器，再將其模塊化并植入汽車鋼板彈簧中，可以在溫度激勵下實現變剛度驅動[3-4]。通過優化植入驅動器的性能和空間布置參數，可以得到最佳變剛度效果和強度，然而在SMA驅動器模塊化植入大型板式結構以實現工程應用的過程中，如何提高優化算法效率是首先要解決的問題。

目前，為了提高模塊化元件布設參數尋優算法的效率，相關學者嘗試將智能算法應用到模塊化元件布設參數的尋優中[5-6]，但上述智能算法在處理大型結構時，都會不可避免地遇到由于布設點的增加、驅動器數量增加等所導致的搜索點過多及目標函數值計算次數過多、時間較長的問題。

基于上述問題，本文提出了采用BP神經網絡[7]預測的方法代替傳統的對目標函數值進行直接計算的方法[8]，并針對BP神經網絡易收斂在局部極小值而得不到全局最優的缺點，進一步通過遺傳算法對BP神經網絡模型進行改善，以提高預測精度，進而提升對于大型板式結構中驅動器最優空間布置參數的尋優效率。

1BP神經網絡模型建立（Establishment of BPNeural Network model）

1.1 數據來源

鑒于篇幅所限，剛度和強度的詳細理論計算將在另一篇論文中深入闡述。但是，本文會引用相關的Matlab計算程序作為支持數據集。

1.2BP神經網絡基本原理

BP神經網絡（Back Propagation Neural Networks）是一種多層的前饋型神經網絡，由于其對誤差的調節是從輸出層逐步往回推進，因此又被稱為誤差反向傳播網絡。BP神經網絡一般由3個神經元層組成，分別為輸入層、隱藏層及輸出層。BP神經網絡通常采用全連接方式，同一層的神經元互不干擾，不同層之間的神經元通過權值等網絡結構參數實現非線性連接。傳統BP神經網絡算法具體分為以下兩個過程[9]。

第一階段是信號的正向傳播過程：將對象的特征信號經由輸入層開始正向傳遞，不同的自變量x1，x2，…，xi 對應不同的權重系數w1，w2，…，wj，為了使模型更好地收斂，引入偏置項自變量x0 為恒定值-1，對應的權重系數為θ，將所有的自變量乘以各自對應的權重系數后求和得到b，將b 經過激活函數處理后得到?（b），上一層神經元的輸出元又作為下一層的輸入，如此進行一系列非線性變換，經由隱藏層神經元傳遞到輸出層神經元，最后將得到的輸出信號與目標輸出信號進行誤差對比分析，若達不到條件，則轉入誤差的反向傳播過程。

第二階段是誤差的反向傳播過程：輸入層x1，x2，…，xi將信號經由隱藏層正向傳播到輸出層后，得到的預測輸出x1，x2，…，xi 與真實值x1，x2，…，xi 之間存在誤差，為了縮小預測輸出與真實輸出之間的誤差，將誤差從輸出層開始，按照正向傳播時的權重系數進行反向傳播，從而根據算法策略對權重系數進行修正。如此循環往復正反向傳播，權重系數得到不斷的更迭，直到前向傳播達到期望輸出，即誤差達到一個滿意值。此時，神經網絡模型完成訓練，可直接對其他樣本進行預測。

1.3BP神經網絡參數設置

BP神經網絡的輸入層是影響板簧剛強度的主要因素，用X 表示;輸出層是影響板簧靜態性能的主要因素，用Y 表示。其分別可以表示如下：

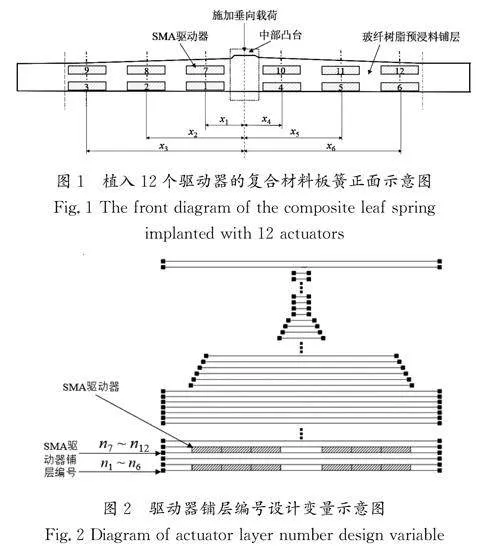
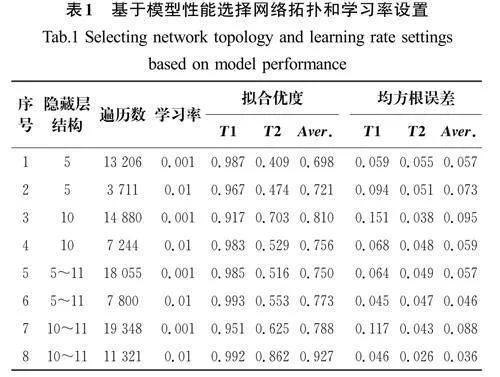
其中：x1，x2，…，x6 為驅動器在板簧中的橫坐標，植入12個驅動器的復合材料板簧正面示意圖如圖1所示。n1，n2，…，n12為驅動器在板簧厚度方向中鋪層的鋪層位置編號，驅動器鋪層編號設計變量示意圖如圖2所示。Δk 為板簧在通電前后的變剛度效果，稱其為第一目標（T1）;R 為板簧的結構強度比，稱其為第二目標（T2）。

在BP神經網絡模型中，輸入層各因素對輸出層各因素的影響程度取決于輸入層各影響因素的權重，通過BP神經網絡的自主學習能力，網絡不斷進行自我訓練和調節，使最終的網絡輸出值不斷逼近實際值。模型的訓練基于Pytorch深度學習框架，采用留出法（Holdout）進行驗證，將整個數據集隨機分成兩個部分，完整的數據集有8 000組，其中7 920組數據作為訓練集，80組數據作為測試集。使用SGD（隨機梯度下降策略）優化算法更新訓練數據中的網絡權重。損失函數采取均方誤差（MSE）來衡量訓練過程中預測值與真實值的匹配程度。隱藏層使用激活函數ReLU，輸出層使用線性激活函數。本文還考慮了網絡拓撲和學習率對模型性能的影響，并開發了幾種網絡模型，這些模型的隱藏層層數和神經元數量各不相同，根據經驗公式判定隱藏單元數的大概取值范圍，進而通過試錯法確定最佳網絡結構，經驗公式如下：

其中：n 為輸入層單元數量，m 為輸出層單元數量，α 為1～10的常數。

常見的回歸模型一般使用R2 系數和RMSE 評估回歸模型的性能。其中，R2 系數又稱擬合優度，通常被用來描述數據對模型擬合程度的好壞，表示自變量對因變量的解釋程度，值域在[0，1]之間，越接近1，說明回歸擬合效果越好。RMSE 為均方根誤差，它衡量了預測值與真實值之間的均方根差異，表示預測值與真實值之間的平均偏差程度。R2 系數和RMSE的計算公式如下：

為了獲得泛化性能良好的模型，需要合理設置完整遍歷數據集的次數，若遍歷次數過少，則有可能發生欠擬合（對于定性數據的學習不夠充分），若太多，則容易發生過擬合（泛化能力不足，在非樣本的數據上表現很差），所以本文引入提前停止功能，在每次遍歷結束后進行一次誤差檢查，如果200次遍歷中，某次迭代下誤差未得到1e-6的改善降低，便提前停止訓練。

1.4 訓練結果總結與討論

在訓練過程中，研究人員嘗試調整損失權重（各個目標損失在總損失中的占比），但是發現這類改變對于擬合效果的改善效果微乎其微，表明兩個輸出之間的任務關聯性較強，存在一定的依賴關系，所以網絡會自動適應重要性不同的任務。本文雖然通過加權求和得到總損失，但是不會考慮損失權重的影響，在BP神經網絡模型中將其設置為1∶1。輸入層神經元數量恒定為18個，輸出層神經元數量恒定為2個，由此對不同隱藏層的層數、不同隱藏層的神經元數量及不同學習率的模型進行了性能評估，基于模型性能選擇網絡拓撲和學習率設置如表1所示。

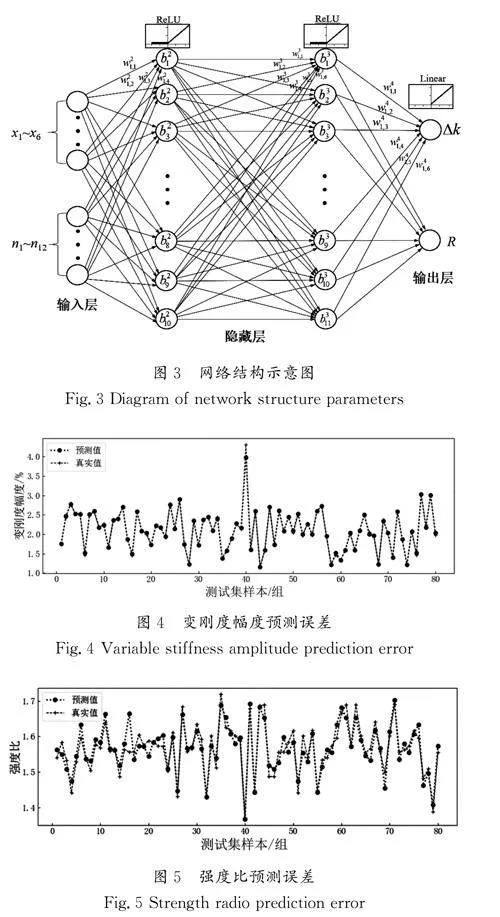
從表1中的數據可知，在經驗公式給出的范圍內，當學習率和隱藏層層數保持一致時，增加隱藏層神經元數量能夠在一定程度上提升網絡性能。通常，學習率越小，意味著極值點越不容易被忽略，但也可能導致進入局部極值點就收斂，并大幅降低收斂速度;學習率過大，意味著有可能找不到極值點，容易在最優解附近振蕩。由表1可知，學習率越大對本文所提網絡的性能改善效果越好，并且具有較快的訓練速度。綜上所述，表1中序號8的網絡結構和參數為最佳模型，其網絡結構示意圖如圖3所示，測試集中預測結果與真實值的對比如圖4和圖5所示。描述T1的預測效果的R2 系數達到了0.992，RMSE僅有0.046。描述T2的預測效果的R2 系數達到了0.862，RMSE僅有0.026。在本文中，T1作為主要目標，傳統BP神經網絡對其預測效果也比較理想，而對T2的預測效果則稍顯不足，因此還需對模型進行改進。

2 GA-BP 算法模擬分析（GA-BP algorithmsimulation analysis）

2.1 GA-BP算法概述

BP神經網絡中存在隱藏單元，雖然在訓練過程中采用了梯度下降的策略對權值進行更新，但是由于無法保證誤差全局最小，因此網絡的權值和閾值可能并非最優。盡管BP神經網絡模型已經具備一定的預測精度，但是為了更準確地預測板簧的靜態性能，本研究采用遺傳算法（GA）[10-11]替代梯度下降策略對BP神經網絡模型的權重和閾值進行優化。遺傳算法基于遺傳學的原理，以遺傳學為理論基礎，通過模擬群體中個體的選擇、交叉和變異等過程，逐步優化問題。引入GA優化BP神經網絡可以很好地解決在BP神經網絡中初始權重選擇范圍大、誤差無法獲取到全局最小值等問題，從而得到一個預測性能和精度更好的網絡模型[12]。

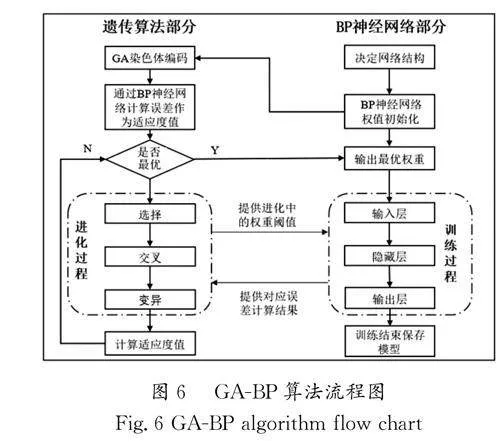
使用GA優化BP神經網絡分為以下3個部分：①BP神經網絡結構的確定;②使用GA進行權值訓練;③進行GA-BP神經網絡模型預測。在已經確定了神經網絡模型結構的基礎上，研究人員采用遺傳算法進一步優化BP神經網絡的權值和閾值，在此過程中，每個遺傳算法的個體均涵蓋網絡的所有權值和閾值，其適應度通過特定的適應度函數進行計算。遺傳算法通過選擇、交叉、變異等操作，篩選出最優適應度值的個體。BP神經網絡預測利用遺傳算法得到的最優個體分配網絡的初始權值和閾值，然后用這些數據訓練網絡，最終獲得預測模型的輸出。GA-BP算法流程圖如圖6所示，GA-BP優化步驟如下。

（1）染色體編碼。根據前文建立的變剛度復合材料板簧性能預測BP神經網絡，將其所有的權值和閾值作為染色體的基因片段，采用分段的實數編碼方式，每個染色體都是一個實數串。所有基因形成染色體向量V=[v1，v2，…，vk，…，vn]，其中[v1，v2，…，vk]是染色體的權重基因，[vk +1，…，vn ]是染色體的閾值基因。

（2）種群初始化。通過BP神經網絡權值和閾值隨機初始化生成對應種群規模的染色體數量。

（3）適應度函數構造。遺傳算法是通過適應度函數模擬大自然中的“適者生存”機制，因此適應度函數要能有效地指導整體優化方向，并且保證不會陷入局部最優或者搜索不收斂的情況。為提升BP神經網絡的泛化能力，在混合訓練中，本文以所有目標樣本的誤差平方和作為染色體個體的適應度值，以獲取更優的初始權值，其公式如下：

其中：yi 是BP神經網絡第i 個輸入特征下的板簧性能的期望輸出值，y^i 是第i 個輸入特征下的板簧性能的預測輸出值，N為目標樣本總數。

（4）選擇策略。遺傳算法的選擇策略有很多種，例如輪盤賭法和錦標賽法。本文中選擇輪盤賭法，具體而言，采用了基于適應度大小進行選擇的概率分配方法，其公式如下：

其中，Fi 為個體的適應度值。由于本文中適應度值代表的是期望輸出與預測輸出的誤差大小，因此該值越小越好，但在輪盤賭中適應度越大的個體，被選中的概率更高，因此在個體選擇之前，需要將適應度值進行轉換，本文進行了倒數處理。fi是轉換后的個體適應度值，pi 是每個個體在輪盤賭中被選擇的概率。

（5）交叉策略。由于本文采用實數編碼的方式對個體進行染色體編碼，交叉操作方法采用簡單的單點交叉方式，通過選擇策略篩選出的個體進行隨機配對，分成父代和母代，再通過隨機選擇交叉點進行基因交換。值得一提的是，為了更好地保證種群的多樣性，本文引入交叉概率，滿足條件則進行如上的單點交叉方式，不滿足條件則直接返回父代和母代。

2.2 參數設置

在已訓練好的網絡結構上，采用遺傳算法對權重進行更新迭代，搜索使目標損失最小的預測模型參數，鑒于本文的模型為多輸出類型，遺傳算法的適應度計算，即目標損失，是通過加權和的方式來確定的。對于變剛度復合材料板簧而言，變剛度效果為首要滿足目標，因此將權值設置成第一目標（變剛度效果）為0.6，第二目標（結構強度）為0.4。初始化時，設置迭代次數為1 000次，種群大小為300，選擇策略采取輪盤賭法，交叉策略采取單點交叉，交叉概率設置為0.95，變異概率為0.1，經過345次迭代后獲得最優結果，其中適應度變化曲線如圖7所示。

2.3 模型評估性能對比

為了更好地觀測預測效果與真實值的誤差，引入絕對誤差計算，公式如下：

其中：y^為預測輸出值，y 為真實輸出值。兩個目標的兩種方法預測誤差對比如圖8和圖9所示。

對比傳統BP神經網絡預測誤差和GA-BP神經網絡的誤差，評價指標結果如表2所示。

從表2中的數據可以看出，GA-BP神經網絡預測模型模擬的擬合優度為0.969，比傳統BP神經網絡預測模型提高了4.5%，均方誤差降低了50%，GA-BP神經網絡預測結果誤差較小，更接近期望目標值，優化效果明顯。

從圖8和圖9中可以看出，對于兩個目標而言，大部分誤差均處于±0.04范圍內，少數達到了±0.06以上，總體符合預測精度要求，并且在大部分測試樣本中，相較于傳統單一使用BP神經網絡模型，經過GA優化的BP神經網絡模型的預測結果誤差更小，更接近真實值，并且具有更準確的變剛度復合材料板簧性能預測結果。

2.4 優化速度對比

將擬合好的神經網絡模型導入Matlab中，與變剛度復合材料板簧的理論模型直接進行計算對比，綜合考慮優化目標變剛度效果和結構強度，對每個驅動器的空間布置參數進行遺傳算法尋優，分為傳統遺傳算法尋優（每次迭代種群中的個體目標值通過理論模型計算得到），GA-BP-GA算法尋優（每次迭代種群中的個體目標值通過預測模型得到）。在相同的計算機配置下優化效率對比如表3所示。

從表3中的數據可知，使用GA-BP神經網絡對個體進行預測代替傳統的對于目標函數值的直接計算，在單次目標值的計算中效率提高了172倍，在總體空間位置尋優中同樣大大提高了效率，優勢明顯。并且，尋優得到的驅動器空間布置參數完全一致，符合優化結果。在更大的板式結構中，隨著驅動器數量和可選位置的增加，尋優效率的提升效果將更加明顯。

3 結論（Conclusion

本文基于傳統智能算法尋優效率低的缺點，提出GA-BP 神經網絡方法，并針對變剛度復合材料板簧中驅動器的空間布置情況進行了分析，通過對比兩個方法對于性能目標的擬合優度和均方根誤差，相較于傳統BP神經網絡方法，經過GA優化的BP神經網絡預測模型的預測精度更高，均方根誤差和平均誤差更小，優化效果明顯，并且其多目標平均預測精度達到96.9%，滿足要求。此預測方法相較于傳統智能算法大大提升了空間位置的尋優效率，為大型板式結構的尋優效率的提升提供了有益的參考。