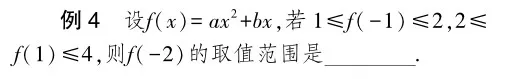高中數(shù)學試卷講評課教學策略探究

【摘要】試卷講評課在高中數(shù)學教學中至關(guān)重要.有效的講評方式，不僅能夠幫助學生在查缺補漏的過程中提升自我，完善知識體系，還有助于教師把握真實學情.基于此，文章在分析當前教學困境的基礎(chǔ)上，以試卷講評課教學應(yīng)遵循的原則出發(fā)，從錯因、思路、方法、變化等角度探討高中數(shù)學試卷講評課教學實踐策略，旨在為教師教學工作的設(shè)計提供參考，提高試卷講評課的質(zhì)量.

【關(guān)鍵詞】高中數(shù)學；試卷講評課；教學策略

引 言

考試能夠暴露出學生在平時學習中的不足之處，教師據(jù)此開展教學活動，引導學生反思，能夠幫助他們查缺補漏，及時糾正錯誤，提高學習成績.但從目前高中試卷講評課來看，教師講得“口干舌燥”，學生聽得“枯燥無味”的情況時有發(fā)生，傳統(tǒng)機械化的講評方式無法滿足學生發(fā)展需求.因此，教師需要結(jié)合學科特點以及學生的學習情況，積極探索新的試卷講評方法，避免學生游離于討論之外，增強學生的參與意識，幫助他們在過程中獲得深層發(fā)展.

一、高中數(shù)學試卷講評課教學面臨困境

（一）就題論題，忽視拓展

試卷講評的目的并非令學生明確自己的錯誤并進行改正，其深層作用是幫助學生明確一類題型的解題方法，養(yǎng)成良好的反思意識與反思習慣，避免日后出現(xiàn)類似的問題.但從目前的講評情況來看，大部分學生都認為在講評課中只要改正自己的錯誤，確保試卷中的題目正確即可，缺乏主動探索以及向上探索的意識，雖掌握基本的知識與技能，但遷移運用能力嚴重不足，如考查題型出現(xiàn)變化，大部分學生還是容易出現(xiàn)錯誤，從而無法發(fā)揮講評課的實際價值.

（二）興趣不足，效率較低

有效的講評課是查、評、講、練、思一體的課.在當前試卷講評課中，大部分學生都存在積極性不足的情況，即一令一動，缺乏思考問題的主動性，習慣依賴教師講授.出現(xiàn)此問題的原因一方面是由于學生對錯題抱有抵觸心理，在出現(xiàn)錯題時學習心態(tài)與學習自信容易受到影響，因此在講評期間可能會存在學習動力不足的情況.而另一方面，傳統(tǒng)“灌輸式”教學會導致學生發(fā)展受限，學生無法在課堂之中獲得豐富體驗，長期處于被動學習狀態(tài)下，主動性難以得到提升，整體教學質(zhì)量偏低.

二、高中數(shù)學試卷講評課教學應(yīng)遵循的原則

試卷講評課能夠讓學生在解題的過程中體會數(shù)學的抽象過程，把數(shù)學價值滲透到現(xiàn)實生活中，體會數(shù)學文化和數(shù)學思想，感悟數(shù)學魅力.數(shù)學試卷講評課在數(shù)學教育課程中不可或缺，教師在組織教學的過程中需要遵循以下原則，為提出符合講評課的教學設(shè)計理念，提供系統(tǒng)的理論指導.

（一）目標性原則

高中數(shù)學試卷講評并非單純地根據(jù)試卷中的錯題進行講解并開展教學活動.一堂有效的試卷講評課必須預設(shè)好合理、清晰的教學目標，建立在學生的最近發(fā)展區(qū)上，遵循目標性原則設(shè)計教學的內(nèi)容、方式、方法，保障學生能夠在目標的指引下完成相對應(yīng)的學習任務(wù)，在查缺補漏的同時實現(xiàn)拓展，進一步提高核心素養(yǎng).

（二）針對性原則

受外部因素影響，在學習中學生的知識生長點、認知能力與思維能力存在明顯的差異，在試卷講評過程中如未關(guān)注到這種差異性，可能會導致班級內(nèi)學生的學習差異逐漸增大.因此，在實踐中教師要遵循針對性原則，關(guān)注學生的實際學習情況，理性分析學生錯誤的成因，有針對性地開展教學，并將考核中經(jīng)常出現(xiàn)的類型作為重點，為學生進行講解，幫助他們在理解知識基礎(chǔ)上靈活的應(yīng)用，更好地發(fā)揮試卷講評課的價值與作用.

（三）激勵性原則

教師應(yīng)學會欣賞學生，善于點燃學生智慧的火花，激發(fā)其內(nèi)在的更大潛能.對于成績稍顯遜色的學生，教師還要善于挖掘他們的閃光點，帶領(lǐng)學生共同尋找失敗的原因，并鼓勵其克服困難，奮起直追，使學生能夠在贊揚中獲得滿足感，增進情感體驗，加強學習自信，從而順利提高學生參與試卷講評活動的積極性，提高整體教學質(zhì)量.

（四）拓展性原則

試卷講評的目的一方面是讓學生查缺補漏，及時調(diào)整自己在學習活動中存在的問題.而另一方面，強調(diào)讓學生把握知識的本質(zhì)，能夠靈活地應(yīng)用所學知識解決問題.因此，在講評課設(shè)計期間，教師需要遵循拓展性原則，在原有教學基礎(chǔ)上對內(nèi)容進行補充、優(yōu)化，為學生設(shè)計并提供豐富的題目類型，啟發(fā)學生通過一題多解、多題一解、變式訓練等方式更好地理解數(shù)學知識之間的內(nèi)部聯(lián)系與規(guī)律，從而在掌握知識與技能的同時，學會解決生活問題.

三、高中數(shù)學試卷講評課教學策略

如何才能提高試卷講評課堂的教學效率？怎樣講評能夠發(fā)揮教學最大效益，幫助學生重拾學習自信？是當前高中數(shù)學教師需要思考的重點問題.下面依據(jù)教學實踐，給出具體的教學策略.

（一）講錯因，讓學生迷途知返

以往直接向?qū)W生宣布答案，勒令學生進行改正的試卷講評方式，難以滿足學生發(fā)展需要，容易限制學生思維生長.在新的試卷講評課中，教師要強調(diào)學生的主體地位，以促進學生高階思維發(fā)展為目標，組織學生對試卷進行分析與討論，交流錯題病因，繼而通過錯因了解自己在知識學習中的薄弱之處，并進行有針對性的鞏固與復習，避免在后續(xù)學習中出現(xiàn)相同的錯誤.因此，在初始講評環(huán)節(jié)，教師要帶領(lǐng)學生共同分析錯題的癥結(jié)，明確錯誤的成因，探索避免錯誤的方法，讓學生“迷途知返”，為后續(xù)學習數(shù)學解題思路以及數(shù)學方法奠定基礎(chǔ).

以“直線的方程”試卷講評課為例.在學習該知識點時，學生需要在理解直線的傾斜角與斜率的基礎(chǔ)上，進一步探索如何用坐標和方程量化點和直線，把圖形的幾何特征轉(zhuǎn)化為代數(shù)表達式.通過對學生試卷的批閱與整理，教師發(fā)現(xiàn)大部分學生在解決這樣一道問題時出現(xiàn)了錯誤：

這樣，錯題即可被輕松化解.總結(jié)期間，教師要引導學生運用思維導圖的方式，梳理在使用直線的截距式方程求直線方程時可能會出現(xiàn)的三種情況，學會具體問題具體分析，避免因忽略截距為零而引發(fā)的解題錯誤.

（二）講思路，使學生柳暗花明

授人以魚不如授人以漁.在試卷講評期間讓學生改正錯誤并非終極目的，令學生建立數(shù)學知識之間的聯(lián)系，明確解題思路，在后續(xù)遇到類似問題時能夠從容應(yīng)對才是關(guān)鍵.因此，在教學期間教師要重點講試題題型的特點和解題的思路.引導學生思考試題考查的方向、數(shù)學知識之間的聯(lián)系以及便捷的解題方法，在解決這些問題后，能夠使學生更好地把握出題人的意圖，提高解決問題的質(zhì)量與效率.

以“平面向量的應(yīng)用”試卷講評課為例.余弦定理和正弦定理是學習的重要內(nèi)容，在練習中，大部分學生在選擇題上都出現(xiàn)了明顯的失誤，比如下題：

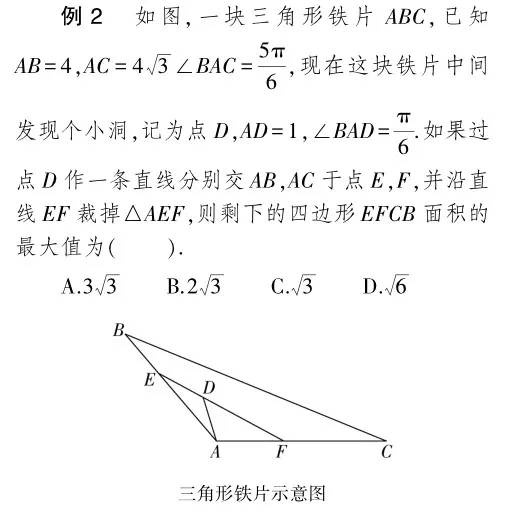
在解決這一問題時，大部分學生都表示按照常規(guī)的解題思路難以得出答案，因此耗費時間較長.對此，教師可以帶領(lǐng)學生探尋簡便的計算思路.本題考查了平面圖形面積的最值，為了簡便運算可以將其轉(zhuǎn)化為求三角形面積的最值問題，將“剩下的四邊形EFCB面積的最大值”轉(zhuǎn)化為“求△AEF面積的最小值”利用正弦定理及基本不等式即可解決.

這樣，學生通過補充練習能夠逐漸領(lǐng)悟“萬變不離其宗”的道理，在知識拓展、延伸的輔助下，通過一道題進而掌握一類題甚至幾類題，如此達到事半功倍的教學效果，有效提高教學質(zhì)量.

（三）講方法，幫學生精益求精

在數(shù)學的學習過程中，學生不僅要掌握基礎(chǔ)知識，更要形成解題思維和解題能力.而“一題多解”的方法能夠幫助學生提高思維能力和深化知識理解.因此，在試卷講評期間，教師不僅要關(guān)注學生容易出現(xiàn)錯誤的題目，還要關(guān)注一些解法多元、思路多樣的數(shù)學問題，帶領(lǐng)學生共同分析，嘗試探索多種解題方法，繼而通過順利解決問題，掌握數(shù)學思想方法在實際解題中的應(yīng)用，繼而幫助學生提高核心素養(yǎng)，使得他們實現(xiàn)精益求精，在不斷追尋真理、探索真相的過程中獲得發(fā)展.

以“二次函數(shù)與一元二次方程、不等式”試卷講評課為例.在本次練習中，教師在試卷上增加了關(guān)于一題多解的內(nèi)容，旨在幫助學生在掌握知識的基礎(chǔ)上，了解數(shù)學思想方法的使用，提高思維的靈活性與發(fā)散性.其中，有這樣一道問題：

例3 當0

除這種解題方法外，教師還可以在班級內(nèi)組織討論活動，引導學生交流：除了可以利用二次函數(shù)解決問題，還可以利用以往學習過的哪些知識解決此題？你認為哪種解題方式最為便捷？在問題的引導下，學生通過討論可能會發(fā)現(xiàn)，此題還有兩種解決方法，即觀察該函數(shù)的結(jié)構(gòu)，可用均值不等式求其最值以及通過求導得到函數(shù)的單調(diào)性，再將函數(shù)的極值與端點值進行比較，從而得到最值.

此外，教師需提醒學生用均值不等式求最值一定要注意三個前提條件，如果無法取到等號那么討論將失去意義.這樣，通過討論能夠幫助學生更好地建立數(shù)學知識之間的聯(lián)系，在探索中掌握一題多解的方法，增強自身解決問題的能力.

（四）講變化，令學生溯本求源

在以往試卷講評中，部分教師習慣側(cè)重對試卷內(nèi)題型的講解，并未進行拓展、連接，導致部分學生思維發(fā)展受到限制，無法抓住問題的本質(zhì)變化，喪失了試卷講評課的實際價值.為此教師在實際講評中不能就題論題，要借題發(fā)揮，善于將原題進行變形，對某知識點從多角度、多側(cè)面、多層次和不同的起點進行提問.讓學生在變式訓練中溯本求源，更好地理解數(shù)學的本質(zhì)，實現(xiàn)高階思維的發(fā)展.

以“基本不等式”試卷講評課為例.講評環(huán)節(jié)，教師選擇試卷中一道經(jīng)典的問題.

此題有兩種解法，即化分式不等式為一元二次不等式（注意分母不能為0），求出集合所表示的范圍，再利用集合知識進行運算，或是利用分類討論法解分式不等式，求出集合所表示的范圍，再利用集合知識進行運算.從解題方法中可以發(fā)現(xiàn)，對于任何分式不等式都是通過移項、通分等一系列手段，把不等式化為0再轉(zhuǎn)化為乘積不等式來解決的.為幫助學生能夠理解知識的本質(zhì)，教師可以對題目進行變化，設(shè)計以下一組變式練習，引導學生在規(guī)定時間內(nèi)解決：

根據(jù)所提供的題組能夠看出.變式1將條件與結(jié)論中嵌入對數(shù)，強調(diào)了方法變式.變式2條件中嵌入三角形，同時變二元線性約束條件為三元線性約束條件，將結(jié)論變?yōu)榉蔷€性目標函數(shù)，強調(diào)了知識變式.在解決以上問題的過程中，學生能夠進一步掌握解分式不等式和一元二次不等式的方法，意識到解分式不等式不能“亂去分母”，只有分母恒為正或恒為負時可去分母.類似地，教師還可以啟發(fā)學生自主依據(jù)變式特點自主設(shè)計問題，在班級內(nèi)進行交流，以此營造良好的討論氛圍，更好地幫助學生在試卷講評訓練中提高學習的自主性，掌握數(shù)學知識的本質(zhì)特點，達成相應(yīng)教學目標.

結(jié) 語

綜上所述，在新高考背景下，組織高中數(shù)學試卷講評教學是促進學生素養(yǎng)發(fā)展，幫助他們查缺補漏，提高問題解決能力的重要途徑.教師需要及時分析當前講評課中存在的問題，并結(jié)合學生的實際學習需求，帶領(lǐng)學生分析錯因，避免類似問題的發(fā)生，在探索中把握數(shù)學問題的解題思路，掌握便捷的數(shù)學思想方法，提高解題質(zhì)量，再根據(jù)不同變化形式靈活地應(yīng)用所學知識處理問題，繼而提高試卷講評課的質(zhì)量，幫助學生在主動參與中獲得深層發(fā)展.

【參考文獻】

[1]顏世芹.“合作學習模式”下的高中數(shù)學試卷講評課探究[J].數(shù)理化解題研究，2023（15）：20-22.

[2]王惠中.在“釋疑解惑”中提高高中數(shù)學試卷講評課的教學品質(zhì)[J].數(shù)學教學通訊，2022（36）：66-67，86.

[3]張禮明，余鐵青.高效開展高中數(shù)學試卷講評課的思考[J].河北理科教學研究，2022（3）：35-38，42.