立足單元整體教學，打造數學高效課堂

【摘要】本文以“因式分解”起始課為例，探討如何在單元整體教學框架下打造高效的數學課堂．通過創設生活情境、總結聯系和區別、借助辨析鞏固概念、在具體中探討方法和依據、繼續探究、動手操作提升思維以及引導回顧等教學環節，讓學生深刻理解因式分解的概念、方法和應用，同時培養學生的數學核心素養和思維能力．

【關鍵詞】單元整體教學；因式分解；高效課堂

1 引言

《義務教育數學課程標準（2022年版）》指出，整體把握教學內容，注重教學內容的結構化，重視單元整體教學設計，體現數學知識之間的內在邏輯關系.所以教師應重視對教學內容、教學內容之間、教學內容主線與相應核心素養發展之間的整體分析[1].筆者在一次教學活動中教授了“因式分解”，進行了單元整體教學的實踐與探索.

2 教學過程

2.1 創設生活情境，通過不同方法計算面積，感受“化積”的獨特作用

學校的實踐課上，老師要求同學們測量學校三處花圃的各邊長度，并計算它們的面積.如圖1所示，以下是同學們的測量結果，你能用不同的方法來計算面積嗎？

問題1 如何計算第一個花圃的面積？

學生1 面積這樣計算：3.7×2.8+3.7×5+3.7×2.2.

學生2 還可以這樣計算：3.7×（2.8+5+2.2）.

問題2 這兩種方法計算的面積相等嗎？哪一種更簡便？

學生齊答 相等，3.7×2.8+5+2.2更簡便.

問題3 如何計算第二個花圃的面積？

學生3 面積這樣計算：5.4 2 +2 ×5.4×4.6+4.6 2.

學生4 還可以這樣計算：5.4+4.62 .

問題4 這兩種方法計算的面積相等嗎？哪一種更簡便？

學生齊答 相等，5.4+4.62 更簡便.

問題5 如何計算第三個花圃？

學生5 面積這樣計算：5.52-2.52.

學生6 還可以這樣計算：（5.5+2.5）×（5.5-2.5）.

問題6 這兩種方法計算的面積相等嗎？哪一種簡便？

學生齊答 相等，5.5+2.5×（5.5-2.5）簡單.

問題7 這些方法更簡便的依據是什么？

學生7 3.7×2.8+3.7×5+3.7×2.2=3.依據是逆用乘法分配律ab+ac+ad=a（b+c+d）.

學生8 5.4 2 +2 × 5.4 × 4.6+4.6 2 =（5.4+4.62）的依據是逆用乘法的完全平方公式a2+2ab+b2=（a+b2）.

學生9 5.52-2.52=（5.5+2.5）×（5.5-2.5）的依據是逆用乘法的平方差公式a2-b2=a+ba-b.

設計意圖 以實際生活情境激發學生學習興趣，讓學生感受到運用數學知識解決生活問題的便捷性.學生在計算中逆運用乘法法則和公式，從數字運算的“化積”的過程向代數式運算的“化積”靠攏，具體感悟“化積”的依據[2].

2.2 分析特點

總結聯系和區別a（b+c+d）=ab+ac+ad ab+ac+ad=a（b+c+d）；

a±b2=a2±2ab+b2a2±2ab+b2=（a±b）2；

a+ba－b=a2－b2a2－b2=（a+b）（a－b）．

問題1 觀察以上三組等式，左邊一列三個等式從左往右看，都發生了怎樣的變形？

學生1 將幾個多項式乘積計算出來寫成右邊的一個多項式化.

問題2 這是我們學習過的整式的什么運算？

學生2 整式乘法.

問題3 觀察以上三組等式，對比左邊一列，右邊一列三個等式從左往右看，都發生了怎樣的變形？

學生3 都是將一個多項式化成了幾個整式的乘積.

師總結 像這樣把一個多項式寫成幾個整式的乘積的過程，叫作多項式的因式分解.

問題4 請思考因式分解與整式乘法有什么聯系和區別？

學生小組交流并總結歸納，如圖2所示.

教師口頭歸納，學生初步感知因式分解的基本方法（見圖3）.

設計意圖 在學生使用簡便方法計算面積的基礎上，類比整式乘法的特征，從形到數引導學生感悟逆運用乘法法則和公式的共同特點.從學生已有的知識經驗出發，建構因式分解的概念，初步建立因式分解的方法的知識框架[3].

2.3 借助辨析，鞏固概念

下列各式從左往右的變形，哪些是因式分解？

1x+2x－2=x22a2－4b2=a+2ba－2b3ab+ac+d=ab+c+d4x2－4x+4=x+2253x2z+6x3y=3x2z+2xy

師生活動 學生完成題目，教師引導歸納.

設計意圖 鞏固學生對因式分解概念的理解，進一步深化對因式分解和整式乘法的互逆關系的認識.

2.4 在具體問題中探討因式分解的方法和依據

學生搶答并總結如何尋找多項式的公因式，如圖4所示.

探究1 將6a3b－9a2b2c分解因式.

問題 你能把多項式的各項寫成公因式與另一個因式的積嗎？

總結 將多項式的每一項分別除以公因式，所得到的項就是另一個因式.

變式1 6a3b－9a2b2c+3a2b.

變式2 －6a3b－9a2b2c+3a2b.

設計意圖 通過問題串與變式的形式引導學生用提公因式法分解因式.

探究2 已知a+b=3，ab=2，求a2b+2a2b2+ab2的值.

練習 把x2+3x+c分解因式，得（x+1）（x+2），則c的值為 .

2.5 繼續探究，拓展思維

拓展1 已知長方形花壇面積為a2+a，一邊長為a+1，你能求出另一邊長嗎？

學生1 長方形的另一邊為（a2+a）÷（a+1）.

教師 你能算出結果來嗎？

學生2 將a2+a寫成aa+1，結果就是a.

教師 a2+a=a（a+1）這一步是在進行什么數學變形呢？

學生齊答 因式分解.

拓展2 你會解這樣的方程嗎？

學生 因為x2－2x=x（x－2），所以x（x－2）=0，所以x=0或2.

教師 這是逆運用整式乘法法則，即體現因式分解是整式乘法的逆變形，后續也會逆運用乘法公式.

設計意圖 引導學生在解決問題中“識別”和“運用”因式分解，進一步認識整式乘法與因式分解是互逆變形的．運用因式分解將學生不熟悉的一元二次方程分解為幾個熟悉的一元一次方程，初步感知“降次”，為后續學習作鋪墊[4].

2.6 動手操作 思維提升

數學實驗：如圖5所示，用1張A型紙片，2張B型紙片，3張C型紙片，拼成一個長為a+2b，寬為a+b的長方形，并根據拼圖的過程將多項式a2+3ab+2b2分解因式.

小組上臺展示拼圖結果，代表1展示部分法求圖形面積a2+3ab+2b2，代表2展示整體法求圖形面積a+2ba+b，代表3總結：a2+3ab+2b2=a+2ba+b.

教師 我們借助拼圖，用不同的方法求圖形面積得出等式a2+3ab+2b2=a+2ba+b，這就是我們今天學習的因式分解，這種方法將是我們今后要學習的十字相乘法.

個等式設計意圖 通過動手操作——拼圖，用不同的方法計算圖形面積，并將其蘊含的數形結合思想方法與因式分解的基本知識相關聯，完善知識基本框架.

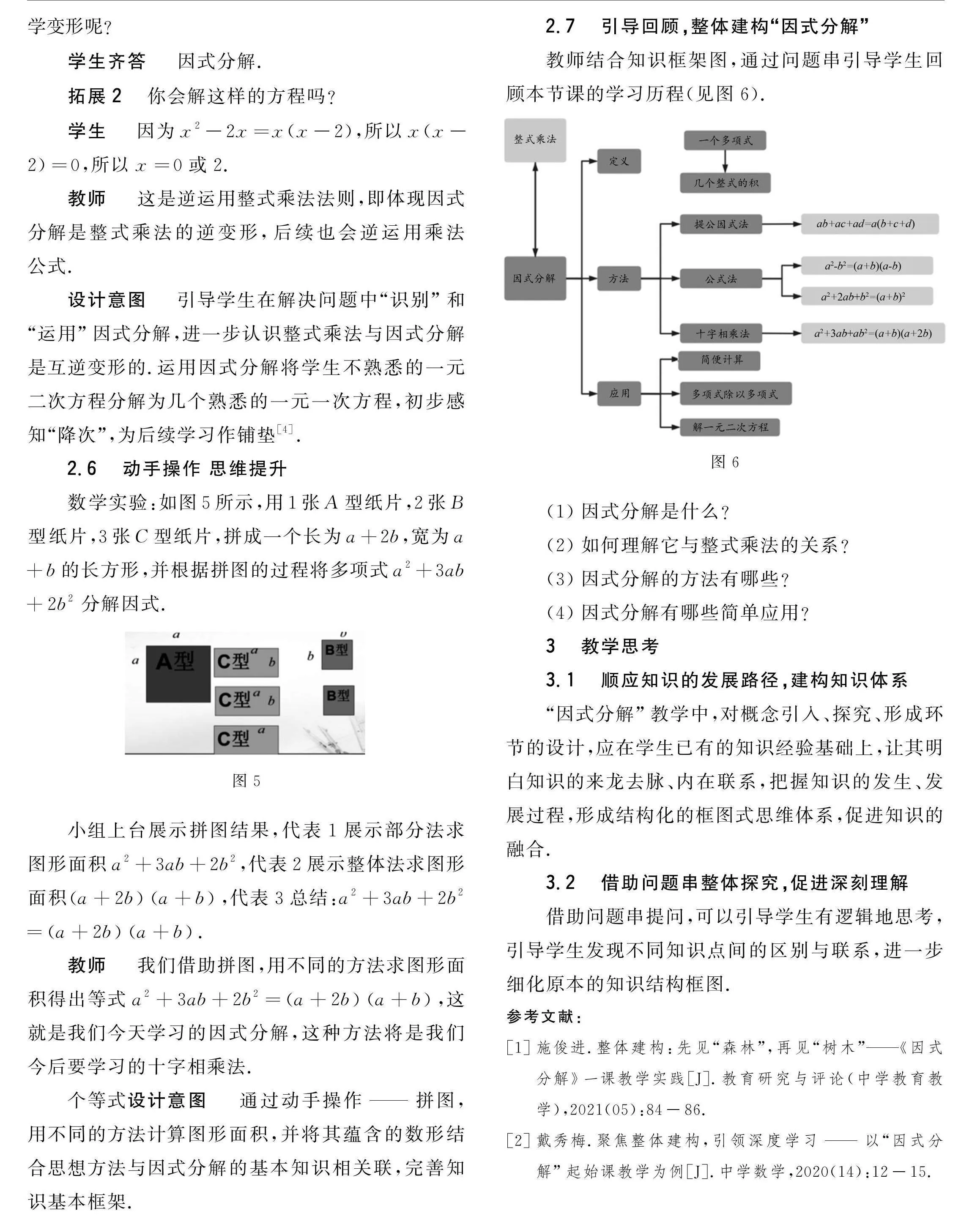
2.7 引導回顧，整體建構“因式分解”

教師結合知識框架圖，通過問題串引導學生回顧本節課的學習歷程（見圖6）.

（1）因式分解是什么？

（2）如何理解它與整式乘法的關系？

（3）因式分解的方法有哪些？

（4）因式分解有哪些簡單應用？

3 教學思考

3.1 順應知識的發展路徑，建構知識體系

“因式分解”教學中，對概念引入、探究、形成環節的設計，應在學生已有的知識經驗基礎上，讓其明白知識的來龍去脈、內在聯系，把握知識的發生、發展過程，形成結構化的框圖式思維體系，促進知識的融合.

3.2 借助問題串整體探究，促進深刻理解

借助問題串提問，可以引導學生有邏輯地思考，引導學生發現不同知識點間的區別與聯系，進一步細化原本的知識結構框圖.

參考文獻：

[1]施俊進.整體建構：先見“森林”，再見“樹木”——《因式分解》一課教學實踐[J].教育研究與評論（中學教育教學），2021（05）：84-86.

[2]戴秀梅.聚焦整體建構，引領深度學習——以“因式分解”起始課教學為例[J].中學數學，2020（14）：12-15.