堿金屬摻雜B0/ ? 18 團簇結構和特性研究

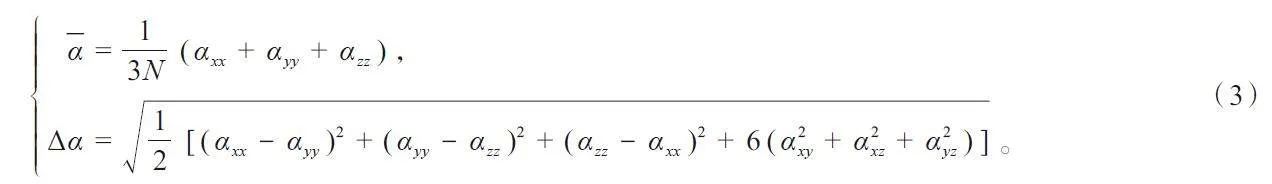
摘要：硼基納米材料因其獨特分子結構和化學鍵成為團簇科學研究的重點。基于卡利普索結構預測程序和密度泛函理論，在PBE0/6-311+G（d）水平下系統分析了堿金屬M2 （M=Li， Na， K）原子摻雜B0/ ? 18 團簇的結構和特性。結構搜索發現，所有全局極小結構均呈現管狀結構。除Li2B18 （C1 點群對稱）外，其他高對稱結構（D9d點群對稱）中2 個摻雜堿金屬原子均位居管兩側的對稱軸線上。基于全局極小結構的穩定性分析表明，K2B18 和Li2B?18 團簇在各自體系中擁有相對高的穩定性。電荷研究發現，摻雜體系中電荷從堿金屬M 原子向硼原子轉移。磁性分析表明，閉殼層電子結構體系（Li2B18、Na2B18和K2B18）總磁矩為0，開殼層電子結構體系（Li2B?1 8、Na2B?18 和K2B?18）分別擁有1 μB 的總磁矩。分析偶極矩和極化率發現，高對稱性結構對應的偶極矩和第一超極化率為0。此外，基于Multiwfn 軟件，擬合出了體系的光電子能譜、紅外譜和拉曼譜。最后，討論了體系的溫度和熱力學參數（定容熱容Cv和標準熵S）之間的關系。

關鍵詞：結構預測；卡利普索；密度泛函理論；特性

中圖分類號：O6 文獻標志碼：A 文章編號：1000-582X（2024）11-120-11

硼是一種典型的缺電子元素，具有原子半徑小、電離能高、配位數大等特點，硼及其化合物表現出明顯不同的結構、化學成鍵和物理化學性質，成為目前團簇科學的研究重點[1-3]。廣泛的理論和實驗研究發現，小尺寸和中等尺寸硼團簇，陽性、中性和陰性分別在硼原子數n<16、20 和25 范圍內呈現平面和類平面結構[4-8]。隨著團簇尺寸增大，陸續發現了碗狀、管狀、籠狀和富勒烯型結構的硼基納米材料[4，7，9-11]。眾多研究發現，利用原子摻雜方式可有效調控硼團簇的結構及各種特性，為尋找新穎構型和特性的納米材料提供了方向[12-21]。例如：不同金屬M（M=Al、Rh、Ir、Co、Ru 和Ta）摻雜B0/ ? 8 、B0/ ? 9 、B0/ ? 10 和B18團簇后形成的平面輪狀結構[12-15]，Al 摻雜B0/ ? 9 和B0/ ? 10 后的傘狀結構[16]，Co 摻雜B16 后的鼓型結構[17]，B20 團簇中摻雜Li、Na、K、Mg 和Ca 后形成的雙環狀結構[18]，Ti 和Sc 摻雜B22 后的籠狀[19]，2 個Li 原子摻雜B24 后的三環管狀[20]，FeB18 及FeB20 呈現的富勒烯型結構等[21]。總之，金屬原子摻雜硼基納米材料表現出的高對稱性、高穩定性和優異特性為設計新穎結構和特性的硼基納米團簇提供了方向。

B0/ ? 18 團簇結構已被實驗和理論驗證，2 種團簇均擁有C3v 點群對稱結構[22-23]。目前，眾多科研工作者已對金屬原子摻雜B0/ ? 18 團簇進行了深入研究[24-30]。Li 等[24]基于實驗的光電子能譜和量子化學計算，研究確定了CoB?1 8 團簇的全局極小為Co 位居三角形B?18 團簇內部的平面結構。化學鍵分析發現，Co 原子和周圍的硼原子之間形成很強的共價鍵相互作用。受平面結構CoB?1 8 團簇啟發，基于第一性原理計算，Li 等[25]對Ni 摻雜B?18團簇的結構和特性進行了研究，得到了同CoB?18 結構相似的C2v點群平面構型，其中Co 原子位居B7環的中心。Jian 等[26]通過實驗測得了RhB?18 團簇的全局極小為鼓狀（D9d點群對稱）和類平面（Cs點群對稱）結構，并從理論上對2 個結構的特征進行了分析，為5d、6d、鑭系和錒系原子摻雜硼基納米材料的研究提供了方向性指導。最近，基于卡利普索結構預測程序，Li 等[27]、Jin 等[28]和Tian 等[29]分別對Mo、Al 和Mg 原子摻雜中性和陰性B0/ ? n （n=10～20）團簇的結構和電子特性進行了系統研究，分別發現了一系列平面、類平面、半夾心、鼓狀和管狀結構。其中，MoB18的全局極小呈現鼓狀結構，其高穩定性主要來源于Mo-4d 和B-2p 軌道之間電子的雜化及B18 結構中的B-B σ 鍵作用[27]。高穩定性AlB?18 具有C2v 點群對稱的環狀平面結構。化學鍵分析表明，其穩定性主要來源于高的HOMO-LUMO 能隙和2 個芳香性的π 鍵[28]。管狀MgB18 高穩定性來源于Mg 原子和B18管之間的相互作用[29]。李成剛等[30]對過渡金屬釩原子摻雜B?18 團簇的結構和電子特性進行了研究，通過卡利普索結構搜索程序和密度泛函理論（density functional theory， DFT），優化得到了VB?18 團簇，其結構由一個管和位于管上方的B2單元構成；分析了電荷轉移和成鍵特性，并擬合出了體系的光電子能譜、紅外和拉曼光譜。除了單原子摻雜B0/ ? 18 團簇外，最近陸續報道了雙原子摻雜B0/ ? 18 團簇的研究[15，31]。例如，基于DFT，Pham 等[15]對2 個4d 和5d 過渡金屬原子摻雜B0/ ? 18 團簇的結構和特性進行了研究。結果發現，摻雜結構呈現陀螺構型，其中2 個摻雜原子分別位居B18管兩側的對稱軸上。Dong 等[31]對2 個堿金屬Na 原子摻雜B0/ ? 18 團簇進行了研究。摻雜體系的結構相對原硼團簇發生了較大改變，分別形成了具有高對稱性（D9d點群對稱）的管狀結構，其中2 個B9環構成管，2 個摻雜的Na 原子分別在管外側的對稱軸上。兩者的區別主要在原子之間Na-B 和B-B 鍵長和相互作用。該研究為金屬摻雜硼基管狀結構的研究提供了重要參考。本文中，基于Na2B0/ ? 18 團簇研究的策略，首先通過卡利普索結構預測程序和DFT，對M2B0/ ? 18（M=Li， Na， K）團簇的結構和特性進行了系統研究。在獲得全局極小結構的基礎上，分析了摻雜體系的穩定性、電子、光譜和熱力學特性。通過對比同族堿金屬原子摻雜B0/ ? 18 硼基材料的結構和特性變化規律，為堿金屬原子摻雜硼基納米材料的實驗和理論研究提供理論基礎和依據。

1 計算方法

結構搜索工作在吉林大學馬琰銘教授課題組研發的基于粒子群優化算法的卡利普索結構預測程序（crystal structure analysis by particle swarm optimization，CALYSPO）基礎上進行[32-33]，對體系的全局極小和低能異構體結構進行搜索。眾多科研工作者已對該程序進行過廣泛驗證[34-39]。程序運行大致如下：1）基于不同的自旋多重度（2s+1=2，4，6），選用PBE（Perdew-Burke-Ernzerhof）泛函和低精度的3-21G 基組；2）根據研究對象，設置對應參數及程序運行的代數和步長；3）運行程序，得到一定量的初始結構（結構的個數由設置的代數和步長決定）；4）從初始結構中選取能量差超過0.3 eV 的50 個結構，再選用高精度的PBE0 泛函和6-311+G（d）基組進行優化[40-41]，最終確定體系的全局極小和低能異構體結構。整個優化過程在Gaussian09 程序下進行[42]。為了確定全局極小結構的合理性，利用ORCA 下的B3LYP-D3/def2-TZVP 方法對PBE0/6-311+G（d）下的全局極小和低能異構體結構進行了重新優化[43]。

2 結果討論

2.1 結構

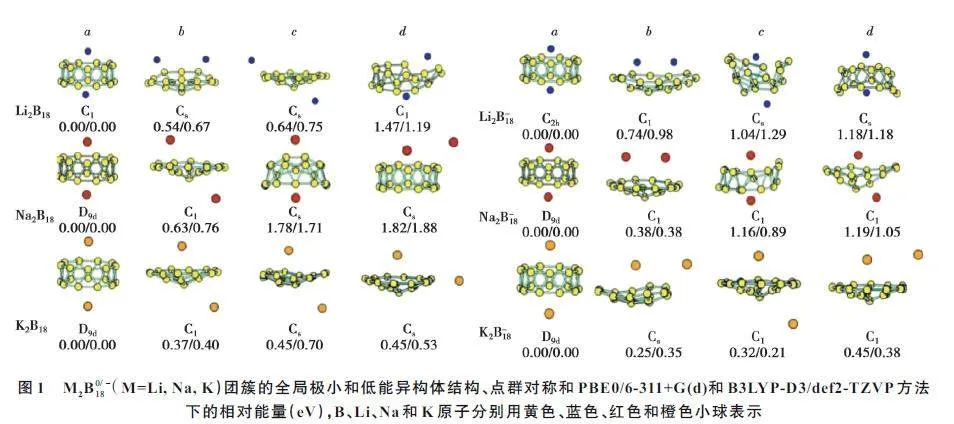
基于Gaussian 下的PBE0/6-311+G（d） 和ORCA 下的B3LYP-D3/def2-TZVP 方法，確定了B0/ ? 18 和M2B0/ ? 18（M=Li， Na， K）團簇的全局極小和低能異構體結構，具體結果見圖1。圖1 中，a、b、c 和d 分別表示PBE0/6-311+G（d）水平下能量從高到低的結構排列。首先，每個團簇中自旋多重度最低時（2s+1=2）的能量最大，本文的研究均在自旋多重度為2s+1=2 下進行。其次，B0/ ? 18 和Na2B0/ ? 18 團簇的全局極小結構同已報道的構型完全相同[22-23，31]，再次證明了本研究中采用的計算方法的合理性。第三，雖然不同方法下前4 個結構的能量出現反轉，但是，2 種方法下的全局極小結構完全相同（能量最大）。第四，所有摻雜體系完全重構了B0/ ? 18 團簇的C3v點群對稱的類平面結構，均呈管狀結構。除Li2B18 中摻雜的2 個Li 原子分別位居管對稱軸線的異側外，其他團簇中，2 個M原子均位居管對稱軸線上，呈現高對稱D9d點群對稱結構。不同管狀結構之間的差異在于M-B和B-B 鍵之間的鍵長大小和相互作用強弱不同，具體參數見圖2 和表1。

由圖2 可知，隨著摻雜原子序數增大，M-M 和M-B 原子之間的距離增大，上下各環中B-B 之間的間距變大，而上下環之間的B-B 距離變小。同時，相對于中性體系，陰性體系下M-M和M-B原子之間間距較小，上下各環中B-B之間間距較小，上下環之間的B-B間距較大。最后，表1 中Wiberg 鍵級的計算結果同鍵長相對應，同類別體系下，原子間鍵長越長，鍵能越小。

2.2 穩定性

對體系的穩定性可通過HOMO-LUMO 能隙（Egap）、平均結合能（Eb）和摻雜能（Ed）分析，其中，Eb和Ed公式如下。

式中，E 為各團簇對應的能量值，計算結果見表1。K2B0/ ? 18 團簇在各自體系中的平均結合能最大，說明K-B 鍵比Li-B 和Na-B 的鍵強，不易被破壞。從Ed和Egap數據發現，K2B18和Li2B?1 8 團簇的能量值較大，意味著K2B18和Li2B?18 團簇在各自體系中的穩定性較高。

2.3 電子特性

2.3.1 電荷轉移

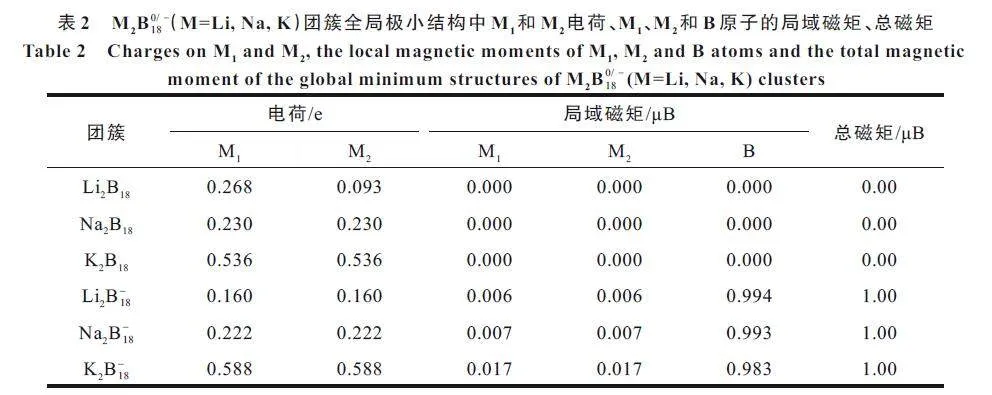
采用PBE0 泛函和6-311+G（d）基組對M2B0/ ? 18（M=Li， Na， K）團簇全局極小結構進行了自然布局（naturalpopulation analysis， NPA）分析，結果見表2。數據發現，2 個M原子均帶正電，所有B 原子均帶負電，說明摻雜體系中電荷從M 原子向B 原子轉移，此特征符合電負性大小關系（B 原子：2.04 eV；Li、Na、K 原子：1.0、0.93、0.83 eV）[44]。而且，對于本研究體系，隨著摻雜原子序數增大，轉移的電荷數增加。

2.3.2 磁性分析

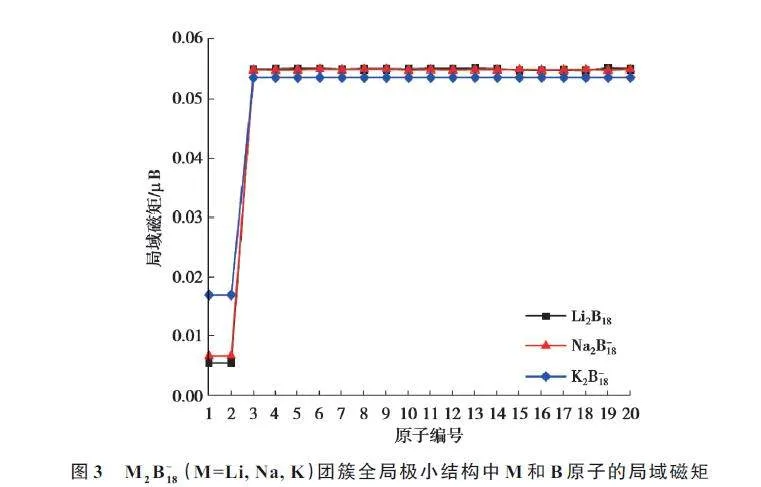
閉殼層體系（Li2B18、Na2B18和K2B18）的每個軌道上均填充2 個電子，電子兩兩配對，總自旋磁矩為0，即發生了“磁矩猝滅”現象，體系不具有磁性。而開殼層體系（Li2B0/ ? 18 、Na2B0/ ? 18 和K2B0/ ? 18 ）中，電子占據不同的α 和β軌道，對應的電子占據數分別為（49，48）（57，56）和（65，64），電子在α 軌道上的占據數比在β 軌道數上的占據數多1 個。由于每個軌道對應一個玻爾磁子，因此，上述體系均擁有1 μB 的總磁矩。此外，圖3 給出了摻雜體系中每個原子的局域磁矩，對比發現，同一體系中，2個堿金屬原子的局域磁矩均相等，所有硼原子的局域磁矩也均相等。而且，每個原子的局域磁矩均為正值，意味著M和B 原子對總磁矩起增強作用，總磁矩主要來自于B 原子局域磁矩的貢獻。此外，對于M2B?18 （M=Li， Na， K）體系，隨著摻雜原子序數增大，摻雜原子的局域磁矩也增大。主要有以下3 個原因：首先，從結構上看，由于電子角動量的對稱性，高對稱性結構（C2h， D9d，D9d 點群對稱）團簇對稱位置上M 原子的局域磁矩相同。對稱性的升高會減小電子帶寬，增強原子的局域磁矩。其次，從轉移電荷數量分析，電荷轉移數越多，原子之間的磁性越強，原子的局域磁矩越大。最后，從原子間鍵長來看，Li、Na、K 原子與周圍B 原子間的距離分別為0.254 1、0.273 7、0.303 6 nm，鍵長越短，說明原子間軌道的波函數交疊越大，電子越多參與成鍵，磁性越低。因此，Li 原子具有較小局域磁矩，K 原子具有較大局域磁矩。

2.3.3 偶極矩和極化性質

偶極矩表征物質分子中正負電荷的分布情況及運行規律，是判斷物質是否存在極性及度量團簇極性大小的常用方法之一。一般說來，偶極矩的大小和對稱性有密切關系，對稱性越高，偶極矩越小。偶極矩μ 計算公式如下。

式中，μX、μY 和μZ 分別表示X、Y、Z 軸方向上的偶極矩分量。由表3 發現，高對稱性結構（D9d點群對稱）的偶極矩為0，而低對稱性Li2B18 （C1 點群對稱）團簇的偶極矩為0.277 Debye（μX=?0.129， μY=?0.143， μZ=0.139）。其中，Y 軸方向上正負電中心偏移距離最大，X 軸方向上正負電中心偏移距離最小，意味著Y 軸對偶極矩的貢獻大，X 軸對偶極矩的貢獻小。

極化率表征體系對外場的響應。本節計算了各向同性平均極化率α、單個原子平均極化率-α和各向異性極化率Δα。

式中：αxx、αyy 和αzz 分別為張量對角元；N 代表團簇尺寸，具體計算結果見表3。首先，陰性體系的平均極化率大于中性體系的平均極化率。而且，該值隨著摻雜原子序數的增大而增大。其中，平均極化率越小說明團簇結構結合越緊密，原子間的相互作用越強，形變程度越小。相反地，K2B?18 的平均極化率最大，說明其在外場作用下最難保持原有的電子云形狀，形變程度最大，非線性光學效應強，易被外場極化。總體系的形變程度大小為：K2B?18>Na2B?18>Li2B?18>K2B18>Na2B18>Li2B18。各向異性極化率表征團簇在外電場中的響應程度，值越大說明體系構型越易受到外場影響。計算結果發現，K2B?18 擁有最大的各向異性極化率，對外場的響應最強，最易受到外場的影響。最后，類似于偶極矩，高對稱結構的第一超極化率β 為0，低對稱Li2B18 團簇具有較大的第一超極化率，說明其具有較強的非線性光學響應。

2.4 光譜特性

2.4.1 光電子能譜（photoelectron spectroscopy， PES）為了輔助全局極小結構的實驗表征，基于廣義的庫普曼定理[45]，利用Multiwfn 軟件[46]，擬合出了B?1 8 和M2B?18 （M=Li， Na， K）團簇在0～6 eV 的PES，擬合結果見圖4。其中，所有峰均采用0.2 eV 高斯半寬進行模擬，每個能譜圖中的第一個峰值所對應的電子結合能為團簇負離子的垂直解離能（vertical detachment energies，VDE），后面的峰對應于來自較低能量軌道躍遷。首先，B?1 8 團簇光電子能譜的理論擬合譜和實驗譜符合很好[23]，說明擬合的M2B?18 （M=Li， Na， K）團簇光電子能譜是可靠的，該軟件的合理性在前期的工作中已得到驗證[3，30，34-35]。Li2B?18 團簇的光電子能譜有4 個明顯的尖峰，分別位于2.06、2.90、3.77、5.71 eV 處。Na2B?18 團簇的光電子能譜有4 個明顯的尖峰，分別位于1.7RAXrpdWicUe2RBQ2DoQnyOfGNTjHiRIR4saSCy89CTk=1、2.72、3.52、5.42 eV 處。K2B?18 團簇的光電子能譜有5 個明顯的尖峰，分別位于1.22、2.49、3.22、5.06、5.96 eV 處。

2.4.2 紅外（IR）和拉曼（Raman）光譜

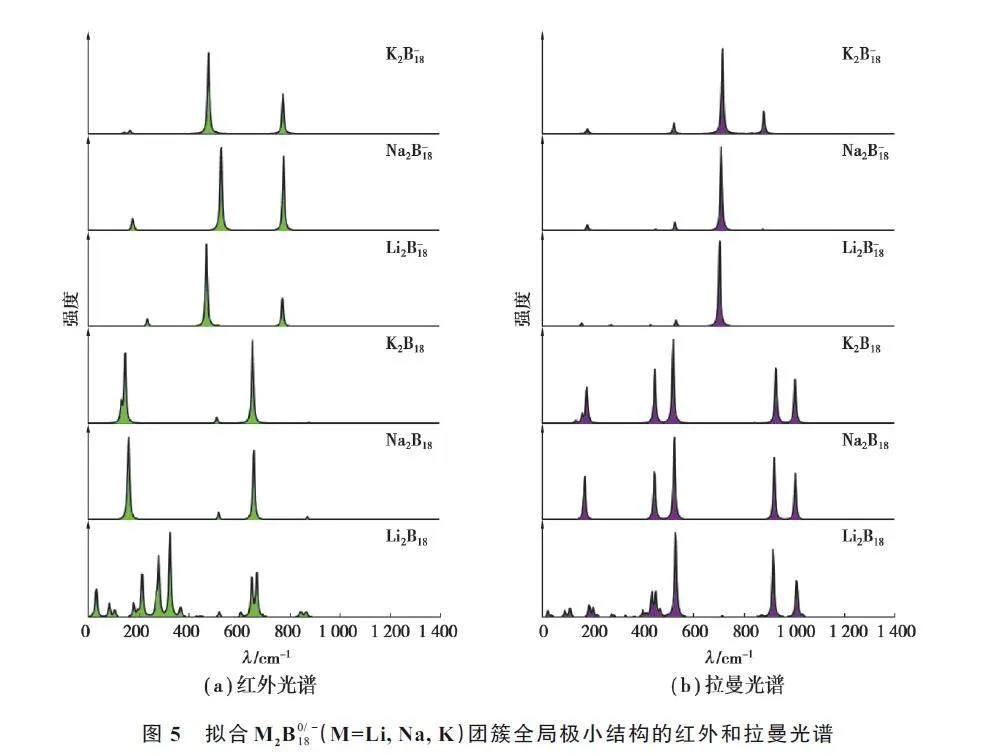
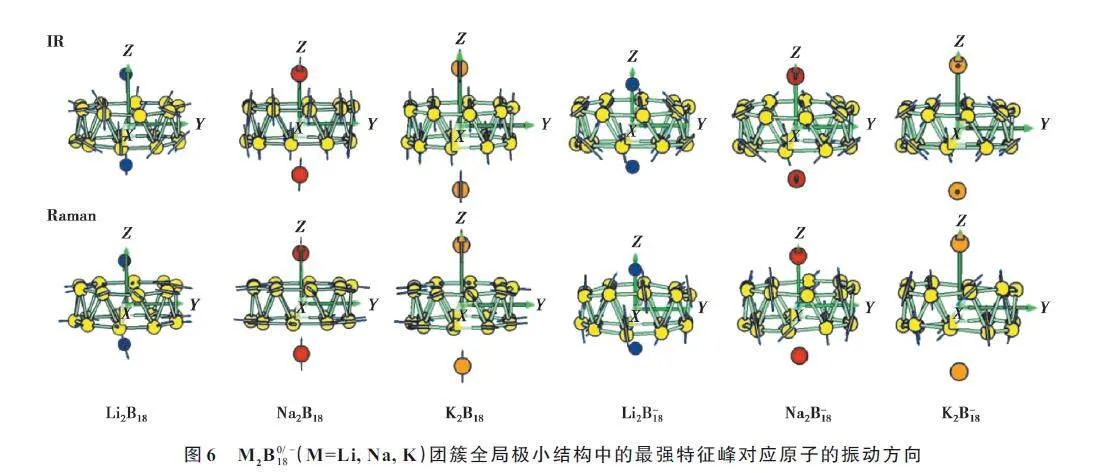
基于全局極小結構，利用Multiwfn 軟件，擬合出了M2B0/ ? 18（M=Li， Na， K）團簇對應的IR 譜和Raman 譜（圖5）。由于同族原子的摻雜，所有體系的振動模式均為54 個。主要特征峰集中在0～1 400 cm?1，陰性團簇最強特征峰對應的頻率高于中性團簇最強特征峰對應的頻率，即多了一個電子后，最強振動峰對應的頻率發生了藍移。Li2B18 團簇中IR 譜的最強特征峰位于327.82 cm?1 處，表現為2 個Li 原子和臨近B9 環間的搖擺振動；Raman 譜的最強特征峰位于527.80 cm?1處，表現為所有原子的呼吸振動模式。對比發現，Na2B18和K2B18團簇的IR 和Raman 最強特征峰振動模式完全相同：IR 譜的最強特征峰（164.46 cm?1和149.87 cm?1）對應2 個Na（K）沿Z 軸的上下往復振動，而所有硼原子的振動和Na（K）原子的振動相反；Raman 譜的最強特征峰（522.43 cm?1和517.53 cm?1）的振動為管中所有硼原子的呼吸振動，而2 個Na（K）原子幾乎保持靜止。對于陰性體系，M2B?18 團簇的IR 譜的最強特征峰分別位于473.67、530.56 和481.04 cm?1 處，表現為所有硼原子的左右搖擺振動；Raman 譜的最強特征峰分別位于702.23、708.75 和712.78 cm?1 處，表現為所有硼原子以XOZ 平面為對稱面的伸縮振動模式。其中，上述2 個最強特征峰振動中的摻雜M（M=Li， Na， K）原子幾乎保持靜止不動。總的來看，陰性團簇較中性團簇的IR 和Raman 譜最強特性峰頻率高，即多了一個電子后，IR 和Raman 最強振動峰對應的頻率發生了藍移。此外，團簇在低頻段內紅外活性好，在高頻段內拉曼活性好。

通過圖6 中不同IR 和Raman 主要特征峰對應原子的振動模式看，每個特征峰產生的原因在于原子的不同振動方向和振幅，而且振動模式和對稱性有關。

2.5 熱力學性質

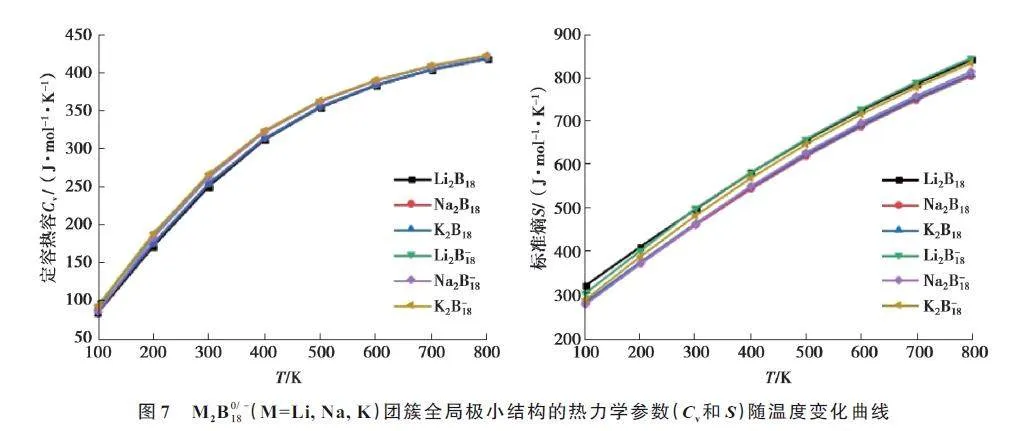
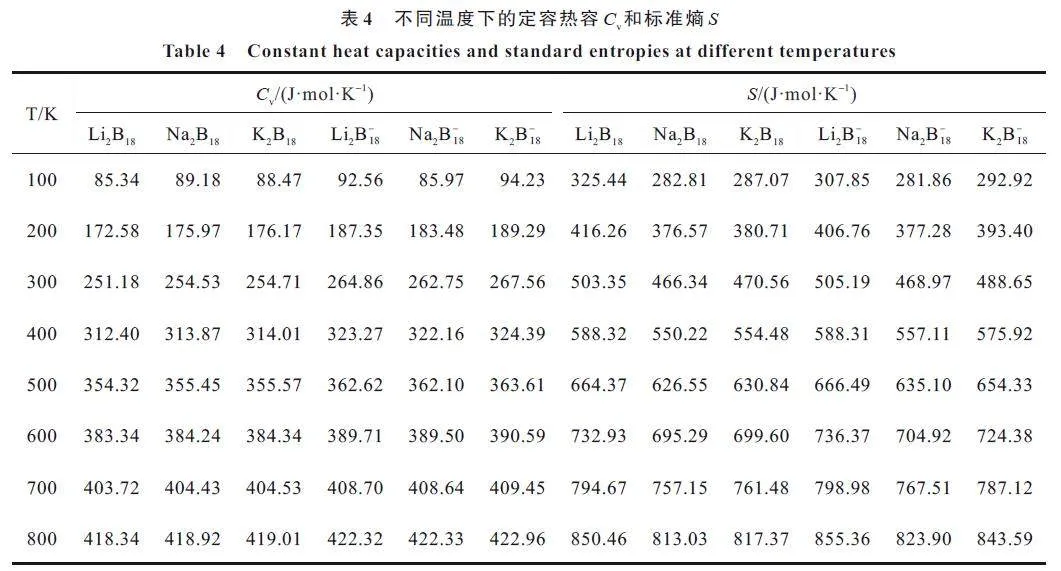
為了探究M2B0/ ? 18（M=Li， Na， K）團簇中溫度對定容熱容Cv 和標準熵S 的影響，分別計算了不同溫度T（100、200、300、400、500、600、700、800 K）下的定容熱容Cv和標準熵S。從表4 和圖7 發現，隨著溫度的升高，定容熱容Cv 和標準熵S 增加。從增加的趨勢看，Cv 和T 之間存在二次函數關系，S 和T 之間存在近似線性關系，具體函數關系如下：

Cv =? 13.968 9 + 1.075 4T ? 6.756 6 × 10? 4T 2， （4）

S = 270.261 8 + 0.753 8T。（5）

式中，對應的測定系數R2分別為0.999 1 和0.992 9。

3 結束語

基于第一性原理計算，系統研究了M2B0/ ? 18（M=Li， Na， K）體系的結構、穩定性、電子、光譜和熱力學性質。結構優化發現，所有摻雜體系均呈現管狀構型，Li2B18 （C1點群對稱）中2 個Li 原子位居管異側不同位置，其他結構（D9d點群對稱）中2 個M 原子位居管兩側對稱軸上。穩定性方面，K2B18和Li2B?18 團簇在各自體系中擁有相對高的穩定性。電荷轉移分析表明，電荷從堿金屬原子向硼原子轉移。而且，隨著摻雜原子序數增大，電荷轉移數增加。對于開殼層電子結構體系（1 μB 的總磁矩），隨著摻雜原子的原子序數增大，摻雜原子的局域磁矩增大。高對稱性結構對應的偶極矩和第一超極化率為0，Li2B18團簇（較大第一超極化率）具有較強的非線性光學響應。K2B0/ ? 18 團簇（較大平均極化率和各向異性極化率）對外場的響應最強，最易受到外場的影響。光譜分析發現，體系的振動模式均為54 個，主要特征峰集中在0～1 400 cm?1，陰性團簇最強特征峰對應的頻率高于中性團簇最強特征峰對應的頻率。熱力學特性方面，定容熱容和標準熵隨著溫度升高而增加，定容熱容和溫度之間存在二次函數關系，標準熵和溫度之間存在近似線性關系。

參考文獻

［ 1 ］ 石勝云， 溫良英， 曹嬌， 等. CO 和Cl2在TiO2（110）表面的吸附行為[J]. 重慶大學學報， 2019， 42（8）： 50-58.

Shi S Y， Wen L Y， Cao J， et al. Adsorption of both CO and Cl2 on TiO2（110） surface[J]. Journal of Chongqing University， 2019，42（8）： 50-58.（in Chinese）

［ 2 ］ 柳楊璐， 劉婷婷， 潘復生. 基于第一性原理的鎂合金合金相及固溶體研究進展[J]. 重慶大學學報， 2018， 41（10）： 30-44.

Liu Y L， Liu T T， Pan F S. Research progress on intermetallic compounds and solid solutions of Mg alloys based on firstprinciplescalculation[J]. Journal of Chongqing University， 2018， 41（10）： 30-44.（in Chinese）

［ 3 ］ 李成剛， 申梓剛， 崔潁琦， 等. V2Si–/0n （n=8～17）團簇幾何結構、穩定性及特性分析[J]. 重慶大學學報， 2024， 47（5）： 122-132.

Li C G， Shen Z G， Cui Y Q， et al. Geometric structures， stabilities and properties of V2Si–/0n （n=8～17） clusters[J]. Journal ofChongqing University， 2024， 47（5）： 122-132.（in Chinese）

［ 4 ］ Piazza Z A， Hu H S， Li W L， et al. Planar hexagonal B36 as a potential basis for extended single-atom layer boron sheets[J].Nature Communications， 2014， 5： 3113.

［ 5 ］ Chen Q， Wei G F， Tian W J， et al. Quasi-planar aromatic B36 and B-36 clusters： all-boron analogues of coronene[J]. Physical Chemistry Chemical Physics， 2014， 16（34）： 18282-18287.

［ 6 ］ Wang L S. Photoelectron spectroscopy of size-selected boron clusters： from planar structures to borophenes and borospherenes[J]. International Reviews in Physical Chemistry， 2016， 35（1）： 69-142.

［ 7 ］ Kiran B， Bulusu S， Zhai H J， et al. Planar-to-tubular structural transition in boron clusters： B20 as the embryo of single-walledboron nanotubes[J]. Proceedings of the National Academy of Sciences of the United States of America， 2005， 102（4）： 961-964.

［ 8 ］ Oger E， Crawford N R M， Kelting R， et al. Boron cluster cations： transition from planar to cylindrical structures[J].Angewandte Chemie （International Edition）， 2007， 46（44）： 8503-8506.

［ 9 ］ Duong L V， Pham H T， Tam N M， et al. A particle on a hollow cylinder： the triple ring tubular cluster B+27[J]. Physical ChemistryChemical Physics， 2014， 16（36）： 19470-19478.

［10］ Pham H T， Duong L V， Tam N M， et al. The boron conundrum： bonding in the bowl B30 and B36， fullerene B40 and triple ringB42 clusters[J]. Chemical Physics Letters， 2014， 608：295-302.

［11］ Zhai H J， Zhao Y F， Li W L， et al. Observation of an all-boron fullerene[J]. Nature Chemistry， 2014， 6（8）： 727-731.

［12］ Li W L， Romanescu C， Galeev T R， et al. Transition-metal-centered nine-membered boron rings： M?B9 and M?B-9 （M = Rh， Ir）[J]. Journal of the American Chemical Society， 2012， 134（1）： 165-168.

［13］ Romanescu C， Galeev T R， Li W L， et al. Aromatic metal-centered monocyclic boron rings： Co?B-8 and Ru?B-9[J].Angewandte Chemie （International Edition）， 2011， 50（40）： 9334-9337.

［14］ Galeev T R， Romanescu C， Li W L， et al. Observation of the highest coordination number in planar species： decacoordinated Ta?B-10 and Nb?B-10 anions[J]. Angewandte Chemie International Edition， 2012， 51（9）： 2101-2105.

［15］ Tan Pham H， Nguyen M T. Formation of the M2Bq 18 teetotum boron clusters with 4d and 5d transition metals M = Rh， Pd， Ir，and Pt[J]. The Journal of Physical Chemistry A， 2019， 123（38）： 8170-8178.

［16］ Galeev T R， Romanescu C， Li W L， et al. Valence isoelectronic substitution in the B-8 and B-9 molecular wheels by an Al dopant atom： umbrella-like structures of AlB-7 and AlB-8[J]. Journal of Chemical Physics， 2011， 135（10）： 104301.

［17］ Popov I A， Jian T， Lopez G V， et al. Cobalt-centred boron molecular drums with the highest coordination number in the CoB16-cluster[J]. Nature Communications， 2015， 6： 8654.

［18］ Ariyarathna I R. Ground and electronically excited states of main-group-metal-doped B20 double rings[J]. The Journal of Physical Chemistry A， 2022， 126（4）： 506-512.

［19］ Celaya C A， Buendía F， Miralrio A， et al. Structures， stabilities and aromatic properties of endohedrally transition metal doped boron clusters M@B22， M = Sc and Ti： a theoretical study[J]. Physical Chemistry Chemical Physics， 2020， 22（15）： 8077-8087.

［20］ Dong X， Jalife S， Vásquez-Espinal A， et al. Li2B24： the simplest combination for a three-ring boron tube[J]. Nanoscale， 2019， 11（5）： 2143-2147.

［21］ Tam N M， Pham H T， Duong L V， et al. Fullerene-like boron clusters stabilized by an endohedrally doped iron atom： B（n）Fewith n = 14， 16， 18 and 20[J]. Physical Chemistry Chemical Physics， 2015， 17（5）： 3000-3003.

［22］ Tai T B， Tam N M， Nguyen M T. Structure of boron clusters revisited， Bn with n =14-20[J]. Chemical Physics Letters， 2012，530： 71-76.

［23］ Sergeeva A P， Averkiev B B， Zhai H J， et al. All-boron analogues of aromatic hydrocarbons： B-17 and B-18[J]. Journal of Chemical Physics， 2011， 134（22）： 224304.

［24］ Li W L， Jian T， Chen X， et al. The planar CoB-18 cluster as a motif for metallo-borophenes[J]. Angewandte Chemie（International Edition）， 2016， 55（26）： 7358-7363.

［25］ Li H R， Tian X X， Luo X M， et al. Heteroborospherene clusters Nin ∈ B40 （n = 1-4） and heteroborophene monolayers Ni2 ∈ B14with planar heptacoordinate transition-metal centers in η7-B7 heptagons[J]. Scientific Reports， 2017， 7： 5701.

［26］ Jian T， Li W L， Chen X， et al. Competition between drum and quasi-planar structures in RhB-18： motifs for metalloboronanotubesand metallo-borophenes[J]. Chemical Science， 2016， 7（12）： 7020-7027.

［27］ Li P F， Du X D， Wang J J， et al. Probing the structural evolution and stabilities of medium-sized MoB0/–n clusters[J]. The Journalof Physical Chemistry C， 2018， 122（34）： 20000-20005.

［28］ Jin S Y， Chen B L， Kuang X Y， et al. Structural and electronic properties of medium-sized aluminum-doped boron clusters AlBn and their anions[J]. The Journal of Physical Chemistry C， 2019， 123（10）： 6276-6283.

［29］ Tian Y H， Wei D H， Jin Y Y， et al. Exhaustive exploration of MgBn （n = 10-20） clusters and their anions[J]. Physical ChemistryChemical Physics， 2019， 21（13）： 6935-6941.

［30］ 李成剛， 申梓剛， 田浩， 等. VB-18 團簇幾何結構及電子特性研究[J]. 分子科學學報， 2022， 38（4）： 321-327.

Li C G， Shen Z G， Tian H， et al. Study of the geometric structure and electronic properties of VB-18 cluster[J]. Journal ofMolecular Science， 2022， 38（4）： 321-327.（in Chinese）

［31］ Dong X， Das A， Liang W Y， et al. Stable global tubular boron clusters in Na2B18 and Na2B–18[J]. RSC Advances， 2019， 9（8）：4665-4670.

［32］ Wang Y C， Lv J， Zhu L， et al. CALYPSO： a method for crystal structure prediction[J]. Computer Physics Communications，2012， 183（10）： 2063-2070.

［33］ Wang Y C， Miao M S， Lv J， et al. An effective structure prediction method for layered materials based on 2D particle swarmoptimization algorithm[J]. Journal of Chemical Physics， 2012， 137（22）： 224108.

［34］ Li C G， Cui Y Q， Li J J， et al. Probing the structural， electronic and spectral properties of a NbB-20 cluster[J]. Molecular Physics，2021， 119（10）：1910744.

［35］ Li C G， Li H J， Cui Y Q， et al. A density functional investigation on the structures， electronic， spectral and fluxional propertiesof VB20? cluster[J]. Journal of Molecular Liquids， 2021， 339：116764.

［36］ Li C G， Cui Y Q， Tian H， et al. Structures， electronic and thermodynamic properties of NiB2n （n=7 – 11） and their anions： atheoretical study[J]. International Journal of Quantum Chemistry， 2022， 122：e26921.

［37］ Li C G， Cui Y Q， Tian H， et al. Quantum chemistry study on the structures and electronic properties of bimetallic Ca2-dopedmagnesium Ca2Mgn （n=1-15） clusters[J]. Nanomaterials， 2022， 12（10）：1654.

［38］ Li H X， Cheng K G， Wang J C， et al. Probing the structural evolution， electronic and vibrational properties of anionic sodiumdopedmagnesium clusters[J]. Computational Materials Science， 2023， 226： 112212.

［39］ Zhao Y R， Xu Y Q， Chen P， et al. Structural and electronic properties of medium-sized beryllium doped magnesium BeMgnclusters and their anions[J]. Results in Physics， 2021， 26： 104341.

［40］ Becke A D. Density-functional thermochemistry. III. The role of exact exchange[J]. The Journal of Chemical Physics， 1993， 98（7）： 5648-5652.

［41］ Krishnan R， Binkley J S， Seeger R， et al. Self-consistent molecular orbital methods. XX. A basis set for correlated wavefunctions[J]. The Journal of Chemical Physics， 1980， 72（1）： 650-654.

［42］ Frisch M J， Trucke G W， Schlegel H B， et al. Gaussian 09[M/CD]. Revision C.01. Wallingford CT： Gaussian Inc.， 2009.

［43］ Neese F. The ORCA program system[J]. WIREs Computational Molecular Science， 2012， 2（1）： 73-78.

［44］ 周公度， 段連運. 結構化學基礎[M]. 北京： 北京大學出版社， 2002： 1-10.

Zhou G D， Duan L Y. Structural chemistry basis[M]. Beijing： Peking University Press， 2002： 1-10.（in Chinese）

［45］ Tozer D J， Handy N C. Improving virtual Kohn-Sham orbitals and eigenvalues： application to excitation energies and staticpolarizabilities [J]. The Journal of Chemical Physics， 1998， 109（23）： 10180-10189.

［46］ Lu T， Chen F W. Multiwfn： a multifunctional wavefunction analyzer[J]. Journal of Computational Chemistry， 2012， 33（5）：580-592.

（編輯 呂建斌）

基金項目：國家自然科學基金資助項目（11904328，12104416）；河南省高等學校重點科研項目計劃（21A460023）；鄭州師范學院本科教學改革研究項目（JXGG-20773）。