電-水耦合系統雙線性加權最小二乘狀態估計

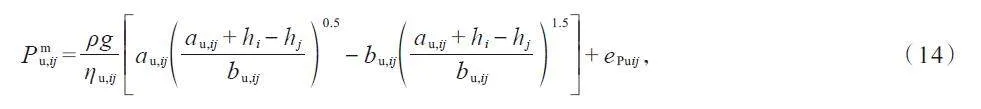
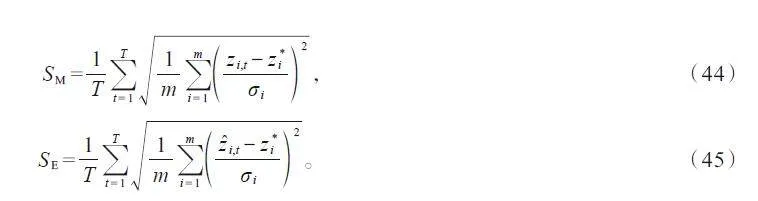
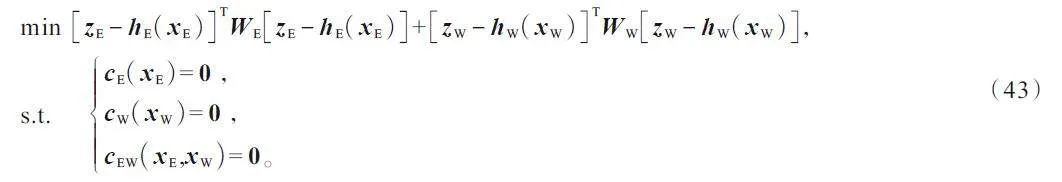
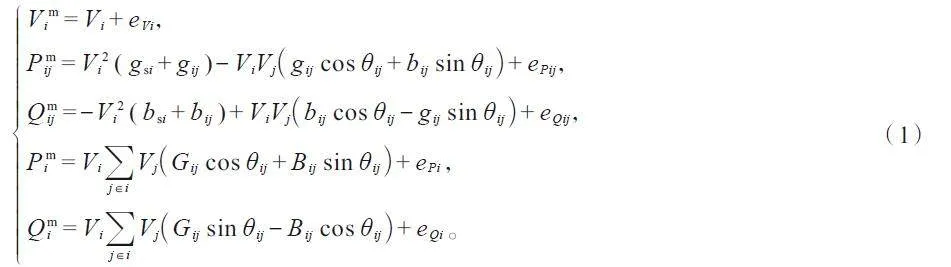
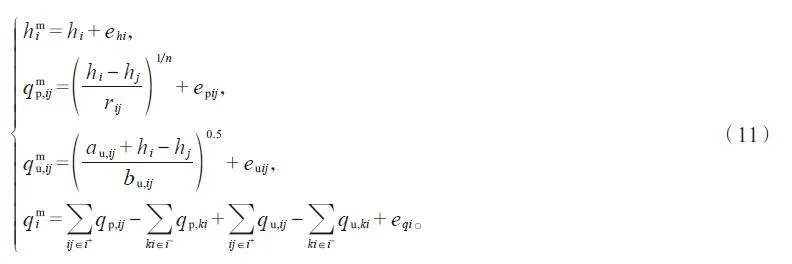
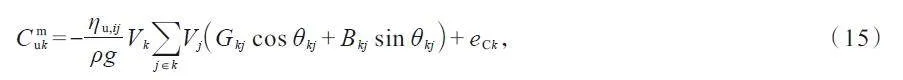
摘要：多能流狀態估計是能源互聯網的重要研究領域。目前，關于電-水耦合系統狀態估計的研究剛起步，還存在對水網工況適應性差、對電-水耦合信息利用不充分等問題。為此，提出一種考慮管道摩阻系數修正的水網雙線性最小二乘（weighted least square，WLS）狀態估計方法，并進一步基于水泵虛擬測量構造電-水耦合信息雙向傳遞，提出適用于電-水耦合系統分立運行、協同運行和聯合運行的雙線性WLS 狀態估計方法。用11 節點水網及其與IEEE-14 節點、IEEE-118 節點電網耦合形成的2 個電-水耦合系統驗證了所提雙線性WLS 估計的有效性。算例結果證明了水網狀態估計中修正管道摩阻系數的必要性與雙線性WLS 估計方法在計算效率與小流量水網適應性方面的優越性，以及協同估計與聯合估計在提升電網/水網狀態估計精度、數據一致性與可觀性方面的有效性。

關鍵詞：能源互聯網；狀態估計；電力系統；水網；最小二乘；雙線性估計

中圖分類號：TM732 文獻標志碼：A 文章編號：1000-582X（2024）11-065-16

能源互聯網以電力、天然氣、熱力系統等多種能源系統互聯互通形成的綜合能源系統（integrated energysystem，IES）為物理載體，以多能互補、開放共享為基本特征，近年來逐漸發展成為能源領域的前沿方向[1]。能源互聯網中多能流系統的高效協同運行與控制需要利用數據采集與監控（supervisory control and dataacquisition，SCADA）系統提供的量測數據，并通過狀態估計來提供完整、可靠、準確的多能流模型與狀態數據來實現。

目前，多能流狀態估計已成為能源互聯網的重要研究內容。國內外學者以電網狀態估計為基礎，結合多能流耦合特性，開展了大量關于多能流狀態估計的研究[2]，涉及電-氣IES[3-5]、電-熱IES[6-8]和電-氣-熱IES[9-10]等多種耦合系統。其中，文獻[3]和文獻[8]是較早關注多能流狀態估計的研究，基于加權最小二乘（weightedleast squares，WLS）方法分別實現了電-熱和電-氣IES 的狀態估計；此后，在多能流狀態估計領域進一步出現加權最小絕對值估計[6]、基于交替方向乘子法的分布式狀態估計[9]等方法。

不僅電-氣、電-熱和電-氣-熱之間存在耦合關系，電網與水網之間也有密切關聯。電力生產需要大量取水，水的取用、處理和輸送需要消耗大量電力（電力驅動水泵耗能占比最大，據統計中國2015 年僅泵取地下水消耗的電能就高達45 800 GW·h[11]）。在能源互聯網背景下，盡管已有大量關于電-水耦合系統潮流[12]、最優潮流[13]及協同調度[14]的研究，但關于電-水耦合系統狀態估計的研究才剛剛起步[15]。

電-水耦合系統狀態估計以電網和水網狀態估計為基礎，需要重點處理電-水耦合環節帶來的新問題。電網狀態估計最早由Scheweppe 教授于20 世紀70 年代提出[16]，目前已有十分成熟的理論和方法；水網狀態估計在很大程度上借鑒了電網的研究思路，也針對水力狀態估計、水質估計、泄漏檢測等特殊問題形成了一系列水網狀態估計方法。與電網類似，水網狀態估計同樣以WLS 估計為基礎[17-22]，分別以節點水頭[18]、環路修正流量[19]為狀態變量，基于節點流量平衡方程[20]或環能量方程[21]建立水網的WLS 估計模型，Bargiela[22]特別針對小流量工況討論了WLS 估計的收斂性問題。可見，無論是電網、水網還是各種IES，最基本且應用最廣泛的狀態估計方法都是WLS 估計，Moazeni 等[15]同樣報道了基于WLS 估計實現電-水耦合系統狀態估計。然而，電網和各種IES 的WLS 估計本質上都是非線性非凸優化問題，存在收斂性問題及全局尋優困難問題[23]。為此，Gomez-Exposito 等[24]提出電網狀態估計的雙線性WLS 方法，通過引入輔助量測量和輔助狀態變量，將原非線性WLS 問題轉化為2 個線性WLS 問題（即“雙線性化”）和一個非線性變換過程；之后，該方法進一步發展為考慮等式約束的雙線性估計方法[25]和雙線性抗差估計方法[26-27]。隨著能源互聯網的發展，雙線性估計方法也從電網狀態估計進一步推廣應用于電-氣IES[28]、電-熱IES[29]及電-氣-熱IES[9]的多能流狀態估計。

如前所述，文獻[15]是目前僅有的關于電-水耦合系統狀態估計的專題研究，但還存在以下局限：1）方法本質上是求解水網和電網2 個非線性WLS 估計問題，難以克服非線性WLS 模型固有的收斂性問題和全局尋優困難；2）僅將水泵功率用于電網狀態估計而未考慮水泵功率對水網狀態估計的作用，對電-水耦合信息的利用并不充分；3）為電網和水網的狀態估計問題的順序求解，未討論耦合系統運行管理模式對狀態估計的影響；4）采用Hazen-Williams（H-W）公式[30]描述管道水頭損失，而H-W 公式對流態及管道粗糙度有一定限制。這些影響了文獻[15]的工程適用性。

水網及電-水耦合系統量測方程的非線性導致其狀態估計是一個非線性WLS 問題，因此，文中將應用雙線性估計的基本思想，研究適用于水網和電-水耦合系統狀態估計的雙線性估計方法。需要指出，熱網含水力和熱力2 個部分，涉及熱網雙線性估計方法的研究（如文獻[9]與文獻[29]），對水網的雙線性化有一定參考意義。但是，熱網水力工況平穩，水壓和流量變化不大，而水網工況取決于水負荷，變化幅度大，對管道方程的適用性要求更高；此外，水網通常需要配置水泵來補償水頭損失，而現有的關于熱網、電-熱IES[6-8，29]及電-氣-熱IES[9-10]狀態估計的研究均未涉及水泵。

文中的主要工作如下：1）提出水網與電-水耦合元件量測方程的雙線性化方案；2）為保證管道方程對水網水力工況的適應性，提出考慮管道摩阻系數修正的水網雙線性WLS 估計方法；3）為適應電-水耦合系統的不同運營模式，提出以水泵虛擬量測實現電-水耦合信息雙向傳遞的雙線性協同估計和聯合估計方法。分別用水網和2 個不同規模電-水耦合系統算例驗證所提雙線性WLS 估計方法的有效性。

1 電-水耦合系統的量測方程

電-水耦合系統量測方程由電網、輸配水網與電-水耦合環節3 部分量測方程組成。電網量測方程以經典交流潮流方程為基礎，以下重點說明輸配水網與電-水耦合環節的量測方程。

1.1 電網的量測方程

考慮電網量測數據為SCADA 系統提供的節點電壓幅值、支路有功/無功功率及節點注入有功/無功功率，以節點電壓為狀態變量，電網量測方程為[23]：

式中：上標m 表示量測量，下標i、j 表示節點i 和節點j，下標ij 表示支路ij；Vi和V mi 分別為節點i 電壓模值及其量測；θij=θi-θj為支路ij 兩端節點電壓相角差；Pmij 與Qmij 分別為支路ij 的有功與無功量測；Pmi 與Qmi 分別為節點i注入有功和無功量測；gij和bij分別為支路ij 的串聯電導和電納；gsi和bsi分別為節點i、j 的對地電導和電納；Gij和Bij分別為節點導納矩陣中節點i、j 對應的電導和電納；j∈i 表示與節點i 直接連接的節點集合；eVi、ePij、eQij、ePi與eQi分別表示下標量測量對應的量測誤差。

記節點電壓模值和相角分別為V = [V1 ，…，VNE ]T、θ = [θ1 ，…，θNE - 1 ]T（下標E 表示電網，上標T 表示轉置，NE為節點總數，平衡節點相角設為0），則電網狀態變量為xE = [V T ，θT ]T，式（1）可記為

zE = hE （ xE ） + eE， （2）

式中：hE（·）表示電網量測函數；zE和eE分別表示電網量測量及其誤差向量。

1.2 水網的量測方程

1.2.1 水網的元件模型

輸配水網又稱給水管網[30] （簡稱水網），主要包含管道、水泵等元件，用節點水頭和支路流量來刻畫其穩態水力特性。文中考慮圓管滿流，管道沿程水頭損失為

Δhp = rqnp， （3）

式中：下標p 表示管道；Δhp為管道兩端節點的水頭差；qp為管道流量；r 和n 分別為管道摩阻系數和水力指數。摩阻系數與管道材質、幾何參數及水流流態等多個因素有關。采用Darcy-Weisbach（D-W）公式時，n=2，摩阻系數為

r =fl/2gdA2 ， （4）

式中：g 為重力加速度；l、d 和A 分別為管道的長度、內直徑和斷面面積；f 為管道摩擦系數，取決于水流流態、管道粗糙度等多個因素。

目前，國內外學者提出了多種計算摩擦系數的方法，其中，Colebrook-White（C-W）公式是適用性及精度最高的公式之一，為

式中：ε 為管壁當量粗糙度；Re 為雷諾數。

雷諾數是表征流態的重要參數，圓管滿流的雷諾數計算為

Re =4qp/πvd， （6）

式中，v 為水的運動粘滯系數。

C-W 公式實質是關于摩擦系數的隱函數。為簡化摩擦系數的計算，水力學分析中通常采用近似顯函數[30]、Moody 曲線[31]等方法。對于處于紊流態（Re>4 000）的較光滑圓管滿流，可用H-W 公式來進一步簡化計算[30]：

f =13.16gd 0.13/C 1.852HW q0.148p。（7）

式中：CHW 為管道的H-W系數（與管道材料、老化程度、斷面橫截面積等參數有關的經驗常數）。

基于H-W公式的管道水頭損失為：

Δw9l4ov0Dne+Hv/WDq+QOPw==hp =（10.67l/C 1.852HW d 4.87）q1.852p 。（8）

沿用式（3）的一般表達，則式（3）中n=1.852，摩阻系數為：

r =10.67l/C 1.852HW d 4.87 。（9）

如前所述，現有關于水網及電-水耦合網絡狀態估計的研究大多采用H-W公式，而H-W公式的適用性有限，可能會影響狀態估計的精度。為此，文中提出基于D-W公式的水網狀態估計方法。考慮到狀態估計對計算時間要求高而C-W公式的計算量較大，因此，筆者采用文獻[32]的經驗計算方法。

水泵通過增加水流壓力來克服管道的摩擦阻力，是實現水流加壓輸送以滿足用戶水壓需求的重要元件。文中采用以下揚程方程[32]來描述水泵的水力特性

Δhu = a - bq2u， （10）

式中：下標u 表示水泵；Δhu 為水泵揚程（水泵兩端節點的水頭差）；qu 為水泵流量；a 和b 分別為水泵關斷水頭和阻力系數，一般通過廠家提供的揚程曲線擬合得到。

1.2.2 水網的量測量及量測方程

與電網類似，輸配水網同樣通過水力SCADA 系統來獲取相關量測數據，典型量測包括節點水頭、管道/水泵流量及節點注入流量[33]。以節點水頭為狀態變量，由管道方程（式（3））、水泵方程（式（10））及節點流量連續性定律，可得量測方程

式中：hi和hmi 分別為水網節點i 水頭及其量測；qp，ij 和qmp，ij 分別為管道ij（即首末節點為i、j 的管道）流量及其量測；rij為管道ij 摩阻系數；qu，ij 和qmu，ij 分別為水泵ij 流量及其量測；au，ij和bu，ij分別為水泵ij 的水力參數；qmi 為節點i注入流量量測；ij∈i+、ki∈i- 分別表示以節點i 為起點及終點的支路集合；ehi、epij、euij與eqi分別表示下標對應的量測誤差。

需要特別指出，采用H-W 公式時，式（11）中摩阻系數rij 為經驗常數；而采用D-W 公式時，由于rij 隨管道流量變化，而管道流量是水頭差的函數（參見式（3）～（6）），管道流量量測函數是關于管道兩端節點水頭的復雜函數。為簡化狀態估計模型同時兼顧狀態估計的精度，基于文獻[32]的經驗計算方法，提出一種考慮摩阻系數修正的水網狀態估計方法。

與電網類似，水網量測方程（式（11））同樣可記為

zW = hW （ xW） + eW， （12）

式中：下標W表示水網；xW = h = [ h1 ，…，hNW ]T為水網水頭向量，NW 為水網節點總數；hW（·）表示水網量測函數；zW 和eW 分別表示水網量測量及其誤差向量。

1.3 電-水耦合環節的量測方程

電力驅動水泵將電能轉化為提升水頭所需的機械能，是最主要的電-水耦合元件。水泵所消耗的功率[15]為

式中：ρ 為水的密度；ηu為水泵功率和效率。

顯然，根據式（13）的電-水耦合關系，水泵流量及水頭量測可參與電網的狀態估計，而水泵功率量測也可以參與水網的狀態估計。文獻[15]僅考慮前者，文中同時考慮2 種情形，以充分利用耦合環節的量測信息。

假設水泵接入水網節點i、j，由式（10）及（13），可構造如下水泵功率量測方程

式中：Pmu，ij 和ePuij分別為水泵ij 的功率量測及其誤差；ηu，ij為水泵ij 的效率。

若水泵ij 由電網節點k 供電，則水泵功率以節點有功負荷形式參與節點k 的有功功率平衡。文中以水泵流量與揚程的乘積（即quΔhu）作為虛擬量測，則有

式中，C muk 和eCk分別為水泵虛擬量測量及其誤差。

設水泵ij 的流量及水頭量測為服從正態分布的獨立隨機變量，即qmu ～ N （μq ，σ 2q ），水頭量測hmi ～ N （ μi ，σ 2i ）、hmj ～ N （μj ，σ 2j ），則揚程Δhmu ～ N （μj - μi ，σ 2i + σ 2j ）。

以Cu=quΔhu作為虛擬量測，則虛擬量測量的方差為

D （qu Δhu ） = D （qu ） D （Δhu ） + D （qu ） E2 （Δhu ） + D （Δhu ） E2 （qu ）， （16）

式中，E（·）和D（·）分別為期望和方差算子。

代入流量及揚程的均值和方差，有：

D （qu Δhu ） = σ 2q （σ 2i + σ 2j ） + σ 2q （ μj - μi ） 2+ （σ 2i + σ 2j ） μ2q。（17）

取流量及水頭表計量測精度作為標準差，并假設水泵量測水頭量測表計的精度一致，則有σi=σj=σh；用流量/水頭量測值來近似其期望，則虛擬量測量方差為：

D （qu Δhu ） ≈ 2σ 2q σ 2h + σ 2q （hmj- hmi） 2+ 2 （σh qmu） 2。（18）

顯然，式（14）與（15）可記為

zuP = huP （ xW） + euP， （19）

zuC = huC （ xE ） + euC， （20）

式中：zuP和euP分別表示水泵功率量測及其誤差向量；zuC和euC分別表示水泵虛擬量測量及其誤差向量；huP（·）和huC（·）分別表示水泵功率及虛擬量測量對應的量測函數。

2 雙線性最小二乘狀態估計原理

2.1 加權最小二乘估計

電網、水網及電-水耦合系統的量測方程均可寫為

z = h （ x） + e， （21）

式中：x、z 和e 分別為狀態變量、量測量及量測誤差向量。

假設各量測量為服從正態分布且相互獨立的隨機變量，基于極大似然估計的狀態估計等價于求解如下WLS 問題[23]。

min [ z - h （ x） ]TW [ z - h （ x） ]， （22）

式中：W為權重矩陣，通常取 W = diag{σ -2i }（σi為第i 個量測量的標準差，diag{·}表示對角陣）。

問題（22）可轉化為如下正則方程的迭代求解[23] （通常稱為高斯-牛頓法）

G（k ）Δx（k ） =[ H（k ） ]TW [ z - h （ x（k ） ） ]， （23）

式中：上標（k）表示第k 次迭代；H 為h（x）的雅可比矩陣，G=HTWH 稱為增益矩陣；Δx 為x 的修正量。顯然，當h（x）為線性函數時，G 為常系數矩陣，求解正則方程無需迭代。

考慮電網/水網的零注入約束及電-水耦合方程時，狀態估計建模為含等式約束的WLS 問題，基于高斯-牛頓法同樣可以轉化為類似式（23）的正則方程的迭代求解，詳見文獻[23]。

2.2 雙線性WLS 估計

對于電網、水網或者電-水耦合系統，WLS 估計本質上都是非線性非凸優化問題，應用高斯-牛頓法可能存在收斂問題及全局尋優困難。為此，文獻[24]提出雙線性WLS 估計方法，其基本思想是通過設置輔助變量將非線性量測函數線性化，從而將非線性的WLS 原問題轉化為2 個線性WLS 問題的順序求解。為簡化表述，下面以不含等式約束的WLS 問題為例說明雙線性WLS 估計的基本原理，等式約束雙線性估計方法詳見文獻[25]。

假設通過引入適當的輔助變量和變換關系，原量測方程（21）可轉化為

z = By + e， （24）

u = f （ y）， （25）

u = Cx + eu， （26）

式中：y 和u 為輔助變量；f（·）為u 和y 之間的變換關系；eu為u 的量測誤差；B 和C 分別表征z、y 及u、x 之間線性變換關系的系數矩陣。

式（24）與式（26）為2 組線性量測方程，式（25）為一組非線性變換。相應地，雙線性估計包含以下3 個階段[24]。

1）以y 為輔助狀態變量，求解式（24）對應的線性WLS 問題，得到y 的估計值y?，即

Gb y? = BTWz， （27）

式中：Gb=BTWB 為式（24）對應的增益矩陣。可以證明，y 的協方差矩陣cov （ y） = G-1b 。

2）計算u 的估計值u? 及權重矩陣Wu為

式中：F 為f（·）的雅可比矩陣；F ? 為F 在y? 處的取值。

3）以u 為輔助量測量，求解式（26）對應的線性WLS 問題，得到x 的估計值x?，即

Gc x? = CTWuu?， （29）

式中：Gc=CTWuC 為式（26）對應的增益矩陣。

對于含等式約束的WLS 模型，應用雙線性方法時需要引入輔助狀態變量將等式約束線性化，并在上述3個階段線性WLS 估計及非線性變換中增廣拉格朗日乘子。

3 電-水耦合系統量測方程的雙線性化

雙線性狀態估計的關鍵在于量測方程的雙線性化，即如何構造輔助變量y、u 實現量測方程的線性化。關于電網的雙線性化已有諸多研究[24-25]，以下重點說明水網及電-水耦合環節的雙線性化方案。下文分別用下標E、W表示電網與水網對應的相關矩陣（例如，用yE、yW 分別表示電網與水網對應的y，余類推）。

3.1 電網量測方程的雙線性化

采用文獻[24]的輔助變量設置方案，取

則有：yE = [U T ，K T ，LT ]T（U、K 和L 分別為Ui、Kij和Lij構成的列向量）。

需要指出，一般來說，yE 的維度大于電網WLS 原問題的狀態變量xE = [V T ，θT ]T，某些情況下可能影響狀態估計的可觀性，這也是雙線性估計方法的固有缺陷。

以節點電壓平方的對數（即αi=2lnVi）及電壓相角為電網狀態變量（即xE = [ αT ，θT ]T），則可以按式（31）設置式（26）中的輔助量測向量uE。

因此，取第一階段水網的輔助狀態向量yW = [ hT ，MT ，N T ]T（h、M、N 分別為節點水頭hi 及支路輔助變量Mp，ij、Nu，ij 構成的列向量），即可將水網原始量測方程zW=hW（xW）+eW（式（12））轉化為線性量測方程zW=BWyW+eW（BW 為水網對應的B 矩陣）。文中以節點水頭為水網狀態變量xW，取各支路水頭差（即Δhij=hi-hj）形成輔助量測向量uW（即取uW=[hT，ΔhT]T），則uW 與xW 之間滿足第三階段所需的線性變換關系，且由水網的節點-支路關聯矩陣即可方便地獲取式（26）中系數矩陣CW。此外，由式（33）可知，管道和水泵的水頭差分別滿足：

由式（35）可導出第二階段所需uW 與yW 之間的非線性變換關系。

不難發現，雙線性估計第一階段以zW 為量測、yW 為輔助狀態向量，第三階段以uW 為輔助量測、xW 為狀態向量，而常規WLS 估計以zW 為量測、xW 為狀態向量；由于yW 及uW 的維度取決于水頭測點數、支路流量測點數及節點流量測點關聯的支路數，其維度可能超過節點數，導致雙線性估計冗余度損失，從而影響雙線性估計的精度甚至可觀性。后文將結合算例具體說明這一問題（參見5.1.2 節）。

3.3 電-水耦合環節量測方程的雙線性化

電-水耦合環節量測方程包含水泵功率量測方程（式（14））和虛擬量測方程（式（15））。其中，虛擬量測方程本質上是節點功率方程，按式（30）設置輔助變量即可實現量測方程的線性化。對于水泵功率量測方程，在輔助變量Nu，ij的基礎上，進一步補充變量Tu，ij：

Tu，ij = （au，ij + hi - hj ） 1.5。（36）

則式（14）轉化為如下線性量測方程：

與3.2 節所述水網的線性化類似，取水泵水頭差作為輔助量測量，則由式（36），有

Δhu，ij = au，ij - T 2 3u，ij 。（38）

可見，式（35）第二式和式（38）即為電-水耦合環節輔助狀態變量與輔助量測量之間的非線性變換關系。

需要指出，由于電-水耦合環節的量測方程并不獨立構成狀態估計模型，因此無須專門針對電-水耦合環節形成雙線性狀態估計所需的y 和u。

4 電-水耦合系統狀態估計的3 種模式及其雙線性估計方法

考慮電-水耦合系統不同的運行管理模式，文中提出分立估計、協同估計和聯合估計3 種狀態估計模式。

4.1 分立估計

分立估計不考慮電網與水網之間的耦合關系，適用于電網與水網分立運行的傳統模式。在該模式下，電網和水網分別獨立進行狀態估計，兩者之間不進行數據交互。

根據電網和水網的量測方程（式（2）、式（12）），考慮零注入約束，分立估計模式下電網和水網的WLS 估計模型分別為：

min [ zE - hE （ xE ） ]TWE[ zE - hE （ xE ） ]，s.t. cE （ xE ） = 0 ；（39）

min [ zW - hW （ xW） ]TWW[ zW - hW （ xW） ]，s.t. cW （ xW） = 0 。（40）

式中：WE和WW分別為電網與水網量測量的權重矩陣；cE（·）和cW（·）分別對應零注入節點的節點功率和流量函數。

顯然，式（39）與式（40）所示的WLS 問題均可應用高斯-牛頓法（以下稱為常規WLS 估計）或者雙線性估計方法進行求解。由于電網與水網獨立估計，常規估計和雙線性估計均可并行求解2 個WLS 問題。

采用雙線性估計方法時，2 個網絡的基本計算步驟同式（27）～（29），此時只需根據3.1 節與3.2 節所述的電網/水網的雙線性化方案，分別代入2 個網絡對應的系數矩陣B、C 及非線性變化關系f（·）進行3 個階段的計算即可。計算過程中，需要將零注入等式約束線性化（線性化方法與節點功率/流量量測方程相同），并在3 個階段的計算中增廣拉格朗日乘子。

需要指出，對于水網狀態估計，若采用H-W 公式，管道摩阻系數為常數且流量量測方程形式較為直觀（參見式（11）），但其適用性有限；采用D-W公式時，由于摩阻系數與雷諾數（管道流量）的函數關系，管道流量量測方程的形式將十分復雜。為簡化水網狀態估計的計算同時兼顧狀態估計模型的精確性，筆者基于文獻[32]的摩擦系數計算方法提出考慮摩阻系數修正的水網狀態估計方法。以雙線性狀態估計為例，所提水網狀態估計步驟如下。

步驟1：輸入水網基礎數據（包括管道/水泵數據、拓撲數據和量測數據等）及收斂精度ε；按定壓節點水頭初始化各節點水頭x（ k ）W （k=0）。

步驟2：根據管道直徑、長度和H-W系數等基本數據，由式（9）按H-W公式計算管道摩阻系數rij。

步驟3：由3.2 節所述水網輔助變量yW 和uW 的設置方案，計算水網系數矩陣BW、CW。

步驟4：求解雙線性估計第一階段的線性WLS 模型，即由（27）計算yW 的估計值y?W。

步驟5：進行雙線性估計第二階段的非線性變換，即由（28）計算uW 的估計值u? W 及權重矩陣Wu。

步驟6：求解雙線性估計第三階段的線性WLS 模型，即由（29）解得水網各節點水頭的估計值x?W。

步驟7：若||x?W - x（ k ）W ||∞ ≤ ε，則結束計算并轉步驟10；否則，令k=k+1，x（ k） W = x?W。

步驟8：根據節點水頭和管道摩阻系數rij，由式（3）與式（6）計算管道流量及雷諾數。

步驟9：應用文獻[32]所述經驗方法，根據管道雷諾數計算管道摩擦因子fij，再由式（4）計算摩阻系數rij，返回步驟3。

步驟10：輸出水網狀態估計結果。

由以上計算步驟可見，步驟3～6 為雙線性估計的計算步驟，而步驟7～9 體現對管道摩阻系數的修正。因此，用高斯-牛頓法計算步驟替換步驟3～6 即得到考慮摩阻系數修正的水網WLS 估計方法，而去掉步驟7～9，則退化為基于H-W模型的水網雙線性估計方法。

4.2 協同估計

與分立估計類似，協同模式下電網和水網狀態估計由各自的調度中心負責運行，區別在于該模式下2 個網絡會交互耦合環節信息。具體來說，水網向電網傳遞水泵虛擬量測量（流量與揚程量測乘積）及其方差，而電網向水網傳遞水泵功率量測及其方差。

協同估計模式下，電網量測方程包含電網原有量測方程（式（2））及水泵虛擬量測方程（式（20））構成，而水網量測方程由水網原有量測方程（式（12））及水泵功率量測方程（式（19））構成。因此，2 個網絡的協同估計WLS 模型分別為：

min [ zE - hE （ xE ） ]TWE[ zE - hE （ xE ） ]+[ zuC - huC （ xE ） ]TWuC[ zuC - huC （ xE ） ]，s.t. cE （ xE ） = 0;（41）

min [ z ] W - hW（ x ） WTWW[ z ] W - hW（ x ） W + [ z ] uP - huP（ x ） WTWuP[ z ] uP - huP（ x ） W ，s.t. cW（ x ） W = 0。（42）

式中：WuC為水泵虛擬量測量的權重（取為虛擬量測量方差的倒數）；WuP為水泵功率量測的權重。

可見，協同估計在分立估計WLS 模型基礎上擴展了與水泵相關的量測方程。當水泵缺乏流量和揚程量測時，電網協同估計模型（41）退化為分立估計模型（39）；而當水泵缺乏功率量測時，水網協同估計模型（42）則退化為分立估計模型（40）。

與分立估計類似，同樣可以采用常規WLS 方法或者雙線性估計方法進行協同估計。對于雙線性協同估計方法，說明以下幾點：

1）與電網分立估計模型（39）比較，協同估計模型（41）擴展了水泵虛擬量測方程（式（20））但不會引入新的輔助量測量和輔助狀態變量，y 和u 的設置同3.1 節的yE和uE。

2）與水網分立估計模型（40）比較，協同估計模型（42）擴展了水泵功率量測方程（式（37））并引入新的輔助狀態變量Tu，ij，因此需要對3.2 節所述水網輔助狀態向量yW 進行擴展，取yW = [ hT ，MT ，N T ，T T ]T（T 為Tu，ij構成的列向量），u 的設置同3.2 節的uW。

3）對水網進行協同估計時，若考慮管道摩阻系數的修正，同樣可采用與上述方案類似的迭代修正策略。

需要特別指出，文獻[15]本質上也是電-水耦合系統的協同狀態估計，但該文需要根據水網狀態估計結果計算水泵功率并傳遞給電網，順序求解水網與電網的狀態估計。與文獻[15]不同，文中的協同估計僅需要傳遞水泵量測信息，電網和水網的狀態估計仍可并行處理，提高了狀態估計的效率。此外，文獻[15]僅考慮在電網狀態估計中利用水泵量測數據，而文中通過電網與水網量測方程的擴展，實現了水泵量測數據的雙向利用，特別是當水網缺乏水泵相關量測時，由電網向水網傳遞水泵功率量測數據將有利于提高水網量測的冗余度并提升水網狀態估計的性能。

4.3 聯合估計

聯合估計適用于電-水耦合系統由統一調度中心負責運行的場景，是電網與水網的一體化估計。統一調度中心同時接收2 個網絡的量測數據，聯合估計的WLS 模型為：

式中，cEW（·）表示電-水耦合約束，對應式（13）的水泵功率方程。

與分立估計和協同估計相比，聯合估計將水泵功率方程作為等式約束，能夠保證狀態估計結果嚴格滿足電-水耦合關系（即獲得全局一致解），但聯合估計模型的問題規模顯著增大。

與分立估計和協同估計類似，同樣可以采用常規WLS 方法或者雙線性估計方法求解聯合估計模型。對于雙線性聯合估計，說明以下幾點：

1）根據3.3 節所述電-水耦合環節量測方程的線性化方法，借助電網輔助變量（Ui、Kij和Lij）和水泵輔助變量（Nu，ij和Tu，ij），即可實現耦合函數cEW（·）的線性化。由于Tu，ij僅與水泵功率方程關聯，雙線性估計需要補充水泵功率量測方程（式（37））作為聯合估計的虛擬量測方程，即此時式（43）中的zW 擴展為[ z TW，z TuP ]T。

2）聯合估計的輔助變量y 和u 分別由3.1 節和3.2 節所述電網和水網對應的輔助變量構成，即y =[ yTE ，yTW ]T，u = [ uTE ，uTW ]T。

3）由于電網與水網的輔助變量并無關聯，因此，雙線性估計的第二與第三階段可以實現電網與水網的解耦計算。

4）當考慮修正管道摩阻系數時，修正方法與分立和協同估計并無區別，但這2 種估計模式只需要迭代求解水網的估計模型，而聯合估計則需要同時對電網雙線性WLS 估計的第一階段進行求解，計算時間可能大幅增加。

5 算例分析

用11 節點水網、IEEE-14 節點電網[34]與11 節點水網耦合形成的電-水耦合系統、IEEE-118 節點電網[34]與2個11 節點水網耦合形成的電-水耦合系統3 個不同規模算例驗證文中雙線性狀態估計方法的有效性。11 節點水網算例接線圖及其與IEEE-14 節點電網的耦合關系如圖1（a）（圖中1 和[1]分別表示節點1 及支路1，下同），IEEE-118 節點電網與2 個水網的耦合關系如圖1（b）所示。算例詳細數據參見文獻[35]。

以3 個算例的潮流解作為量測真值（水網潮流通過水力分析軟件EPANET[32]求解），在潮流真值上疊加量測誤差（均值為0，標準差已知的正態分布隨機變量）形成量測值。通過蒙特卡羅抽樣產生量測值樣本，用以下統計指標表征狀態估計的精度：

式中：T 為蒙特卡羅樣本總數（文中取T=3 000）；m 為測點總數（即量測向量z 的維度）；下標i、t 分別對應第i 個測點、第t 個樣本；z *i 和σi分別為測點i 的真值和標準差；zi，t和z?i，t 分別為測點i 在第t 個樣本中的量測值和估計值（z?i，t = hi，t （ x? ））。

可見，SM 和SE分別表示量測誤差和估計誤差的統計值。對于正常的量測系統和狀態估計，有SM≈1，SE<1；若SE/SM<1，表明通過狀態估計減小了測點的誤差，實現了狀態估計的濾波目的，且比值越小，濾波效果越好[23]。

5.1 算例1∶11 節點水網

算例1 驗證管道摩阻系數修正對水網狀態估計結果的影響及所提水網雙線性估計方法的有效性。

5.1.1 修正管道摩阻系數的影響

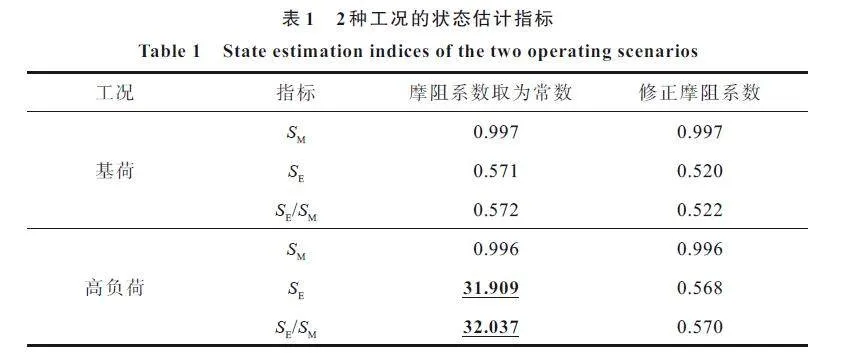
假設算例1 全部節點均配置水頭及流量量測、全部支路均配置流量量測（即全量測配置）；取水頭、支路流量及節點流量量測的標準差分別為0.1 m、0.001 m3/s 及0.003 m3/s。以文獻[35]負荷為基荷，考慮基荷和高負荷（負荷流量為基荷的5 倍）2 種工況，應用文中雙線性方法對算例1 進行狀態估計。2 種工況的狀態估計指標如表1 所示。其中，“管道摩阻系數取為常數”相當于采用H-W管道方程。

由表1 可見，在基荷情形下，是否修正管道摩阻系數對狀態估計指標的影響不大。在高負荷情形下，若摩阻系數依然取為常數，則SE及SE/SM 指標均顯著大于1（見表1 中下劃線數據），狀態估計未取得濾波效果，這是因為H-W方程的適用性有限，當管道流量較大時，常數摩阻系數無法準確刻畫管道的水力特性；此時，若按文中方法對管道摩阻系數進行修正，則可以有效降低SE及SE/SM指標，保證狀態估計的濾波效果。

表1 結果表明，為保證水網狀態估計對工況的適應性有必要修正管道摩阻系數，同時驗證了文中按經驗方法修正管道摩阻系數的有效性。

5.1.2 雙線性WLS 估計與常規WLS 估計的對比

1）不同量測配置（冗余度）下的估計精度。

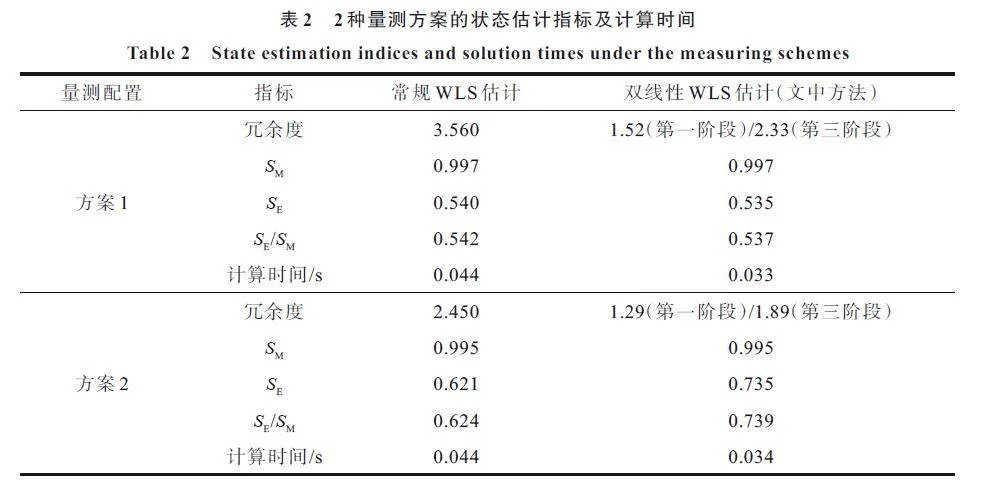
考慮全量測（方案1）和非全量測（方案2，圖1（a）中水網僅奇數號節點配置節點流量量測、奇數號管道配置流量量測，其余量測同方案1）2 種配置方案，量測量標準差同5.1.1 節。分別應用常規WLS 估計和文中所提雙線性WLS 估計對算例1 進行狀態估計，常規方法以水頭量測值作為初值（對于無水頭量測節點，根據定壓節點水頭按一定水頭差設置初值），2 種方法均考慮管道摩阻系數的修正。2 種方法的狀態估計指標及平均計算時間如表2 所示，表中冗余度取量測數與狀態變量數的比值[24]。

由表2 可見，在2 種量測配置方案下，雙線性WLS 估計的冗余度均明顯低于常規WLS 估計，但2 種方法的SE/SM 指標均小于1，表明雙線性WLS 估計和常規WLS 估計均能有效實現濾波；計算時間方面，文中方法較常規方法減少約25%，計算效率提升明顯。進一步對比估計精度可見，方案1 中雙線性估計的精度略優于WLS 估計，表明在全量測配置下，雙線性WLS 估計中冗余度下降對估計精度的影響不大；與方案1 比較，隨著量測量減少，方案2 下2 種方法的SE/SM 指標均有不同程度增大，而雙線性WLS 方法指標的增幅更大，表明雙線性WLS 方法的估計精度受量測配置的影響更大。

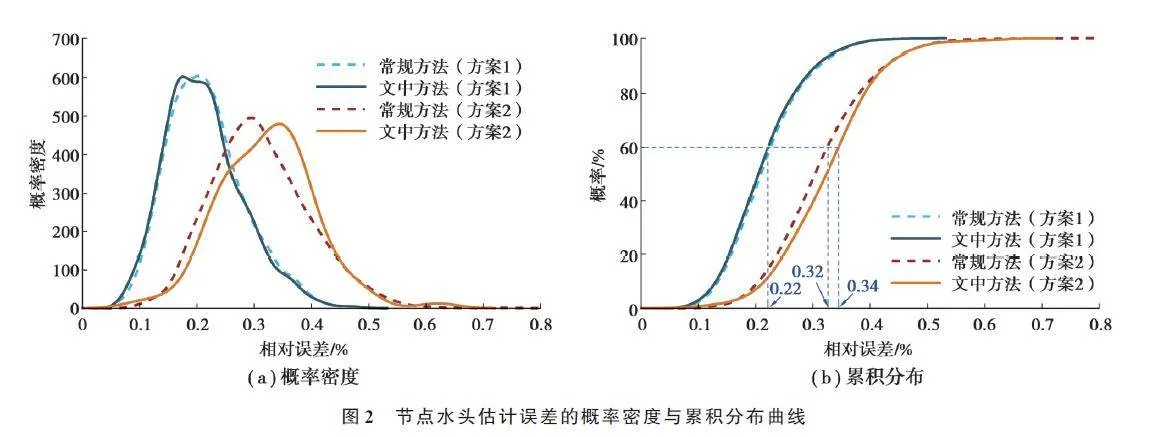
為進一步對比2 種方法的估計精度，按式（46）計算第t 個樣本的節點水頭估計誤差。

式中，h ?i 和h*i 分別為節點i 水頭的估計值和真值。3 000 次抽樣所得εt 的概率密度及累積密度曲線如圖2所示。

由圖2 可見，方案1 中2 種方法的概率密度和累積分布都非常接近，最大估計誤差（εt 的最大值）小于0.6%，絕大多數樣本的估計誤差小于0.4%（60% 以上樣本的誤差小于0.22%）；與方案1 比較，2 種方法的估計精度有不同程度下降，其中，2 種方法的最大估計誤差增加到0.8%，常規方法60% 樣本所對應的估計誤差為0.32%，而文中方法的這一指標為0.34%，再次證明量測量減少對文中方法精度的影響更大。

2）對小流量工況的適應性。

當水網中部分管道流量較小時，以節點水頭為狀態變量的水力學分析可能因為雅可比矩陣條件數過大而導致收斂困難[22]。文中雙線性WLS 估計方法同樣以節點水頭為狀態變量，為分析文中方法對小流量工況的適應性，以算例1 基荷工況為基礎，將節點11 的負荷減小到1/10。在全量測配置（量測量標準差同5.1.1 節）下，2 種方法3 000 次抽樣所得狀態估計指標如表3 所示。

由表3 可見，小流量工況下，常規WLS 方法的收斂性明顯惡化，3 000 個樣本中僅570 個樣本收斂，而其中有效濾波（SE/SM<1）樣本僅有21 個（占比0.7%）；文中方法將非線性WLS 估計問題轉化為線性問題，無需迭代求解（不存在收斂性問題），且僅有6 個樣本未實現有效濾波，估計性能較常規方法有明顯提升。

5.2 算例2：IEEE-14 節點電網+11 節點水網

本節以電-水耦合系統為算例，驗證所提雙線性估計方法對電-水耦合系統的適應性，并對比分析3 種估計模式對耦合系統狀態估計精度及可觀性的影響。

5.2.1 3 種模式的狀態估計指標

假設電網中各節點配置注入有功及無功量測、偶數號節點配置電壓量測、偶數號支路配置首端有功和無功量測、奇數號支路配置末端有功和無功量測；取電壓和功率量測的標準差（標幺值）分別為0.005 和0.010。水網中各支路配置流量量測、奇數號節點配置水頭量測和注入流量量測，各量測量標準差同5.1.1 節。

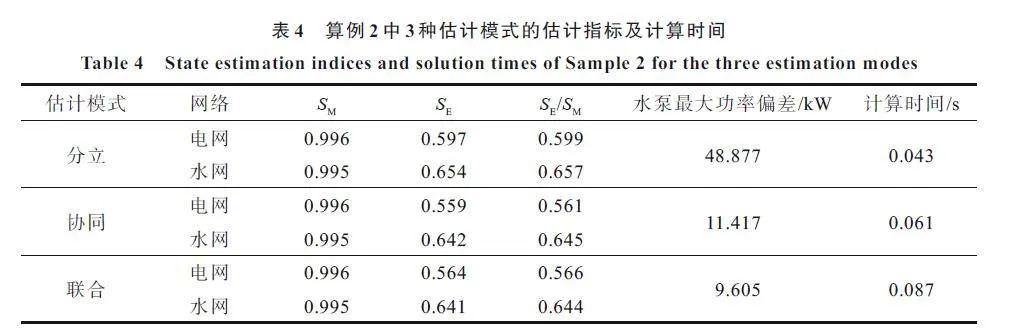
考慮管道摩阻系數修正，應用雙線性估計方法對算例2 分別進行分立估計、協同估計和聯合估計。3 種模式下，分別統計電網與水網的狀態估計指標；此外，分別根據電網與水網的估計結果計算水泵功率，用兩者之差來表示水泵功率估計偏差，取2 臺水泵功率偏差的最大值來表征電-水耦合環節的不匹配程度。3 種模式的指標及平均計算時間如表4 所示。

由表4 可見，文中的雙線性方法能有效實現3 種模式的狀態估計，驗證了文中方法對電-水耦合系統狀態估計的適應性。此外，3 種模式的SE/SM指標、水泵功率偏差和計算時間均有明顯差別，具體說明如下。

從SE/SM 指標來看，與分立估計比較，協同估計和聯合估計模式下電網和水網的SE/SM 指標均有明顯下降，表明協同估計和聯合估計均有利于提升電網和水網的狀態估計精度。此外，對比協同估計與聯合估計可見，水網的估計精度相當，但電網聯合估計的精度有所下降。

從水泵功率偏差來看，由于分立估計模式下電網和水網不交換電-水耦合環節的相關數據，水泵功率偏差最大。協同估計模式下電網與水網交互虛擬量測與功率量測，聯合估計模式將水泵功率方程作為狀態估計的等式約束，2 種模式均能大幅降低水泵功率偏差，從而提升電-水耦合環節的數據一致性。

從計算時間來看，分立估計、協同估計和聯合估計的用時依次增加，這是因為分立估計優化問題的規模最小，聯合估計的規模最大，而協同估計的問題規模居中。由于3 種估計均采用雙線性方法，且聯合估計第二與第三階段可實現電網與水網的解耦計算，因此，3 種模式的計算時間相差并不大。

5.2.2 3 種模式對可觀性的影響

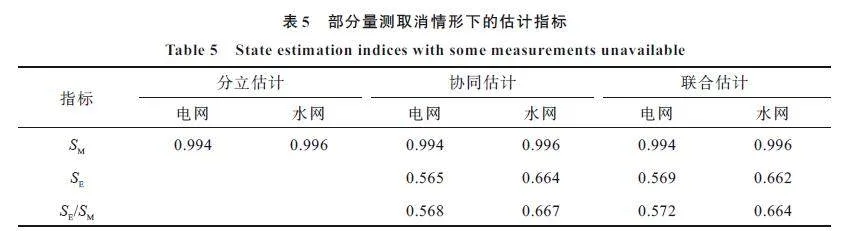
在5.2.1 節量測量基礎上，取消電網節點10（水泵[1]的供電節點）的電壓和注入功率量測，以及與節點10關聯所有支路的功率量測，取消水泵[2]及其關聯支路[11]的流量量測和節點7 的水頭量測，其余量測配置及標準差同5.2.1 節。應用文中的雙線性方法對電-水耦合系統進行狀態估計，3 種模式的狀態估計指標如表5所示。

經可觀性分析可知，電網節點10 和水泵[2]網側節點（水網節點10）均不可觀測，因此，無法通過分立估計對電網和水網進行狀態估計。協同模式下，水網向電網傳遞水泵[1]的虛擬量測，相當于補充了電網節點10的注入有功量測，而電網向水網傳遞水泵[2]的功率量測，相當于補充了與水泵[2]流量和網側節點（節點10）水頭有關的量測，因此，協同模式下電網和水網均可觀測。聯合估計將2 臺水泵的功率方程作為等式約束，相當于同時擴展了電網節點10 與水泵[2]與耦合系統狀態變量的關聯關系，同樣使電網和水網可觀測。

需要特別指出，文獻[15]的方法將水泵功率傳遞給電網，同樣可以改善電網的可觀性；但文獻[15]缺乏電網到水網的反向數據傳遞，水網仍不可觀。文中考慮了電網與水網之間數據的雙向傳遞，可以同時改善電網和水網的可觀性。

5.3 算例3：IEEE-118 節點電網+2 個11 節點水網

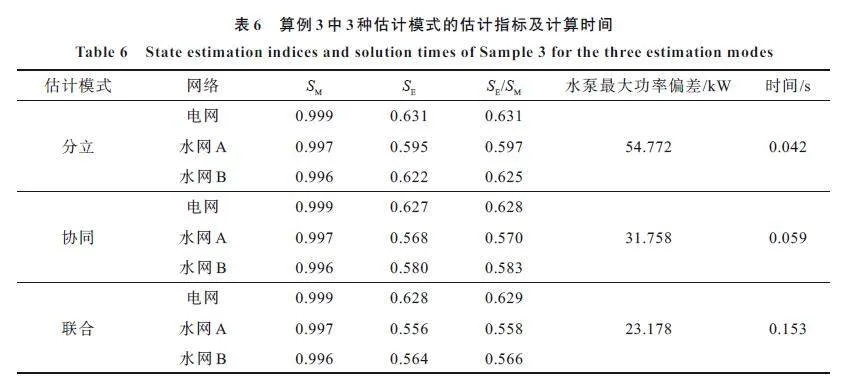
假設算例3 中IEEE-118 節點電網中各節點配置注入有功量測與電壓量測、各支路配置首端有功和無功量測，電壓和功率量測的標準差同5.2 節；水網A 中各節點配置水頭量測和注入流量量測、奇數號支路配置流量量測（水頭、支路流量及節點流量量測的標準差分別為0.1 m、0.01 m3/s 及0.03 m3/s）；水網B 中僅在奇數號節點處配置水頭量測，其余量測配置及量測標準差同水網A。應用文中雙線性方法對算例3 進行狀態估計，3種模式的估計指標及計算時間如表6 所示。

由表6 可見，3 種模式下雙線性WLS 估計方法均能有效實現電網和2 個水網的狀態估計，驗證了文中方法對較大規模電-水耦合系統狀態估計的適應性。

從SE/SM 指標和水泵功率偏差來看，與分立估計比較，協同估計和聯合估計下電網及2 個水網的SE/SM 指標有不同程度降低，而水泵功率偏差明顯減小，這些結果與算例2 類似，再次驗證協同估計和聯合估計有利于提升電網和水網的估計精度，以及電-水耦合環節的數據一致性（且聯合估計在改善水網估計精度、提升數據一致性方面具有更明顯的優勢）。

從計算時間來看，3 種模式下雙線性方法均能快速實現算例3 的狀態估計，與常規WLS（分立估計和協同估計用時0.770 s，聯合估計用時2.612 s）比較，雙線性估計的用時低于WLS 估計的8%，計算效率優勢較為明顯。此外，對比算例2（見表4）的計算時間可見，分立模式和協同模式的計算時間略有增加，而聯合模式的時間增幅較大，這是因為分立估計和協同估計只需要分別修正2 個水網的摩阻系數，而聯合估計的迭代修正流程要求2 個水網同時滿足收斂條件時才停止迭代，導致估計時間增加；總體來說，對不同規模算例，雙線性方法的計算時間變化不大，在計算效率上表現出良好的適應性。

6 結 論

文中提出考慮管道摩阻系數的水網雙線性估計方法，并進一步考慮電-水耦合系統的分立運行、協同運行和聯合運行3 種不同模式，提出電-水耦合系統的雙線性估計方法。用11 節點水網及其與IEEE-14 節點、IEEE-118 節點電網耦合形成的電-水耦合系統驗證了文中雙線性估計方法的有效性。算例結果表明：

1）為保證狀態估計對水網工況的適應性，有必要在狀態估計中考慮管道摩阻系數的修正。

2）與常規WLS 估計方法比較，文中雙線性估計方法具有計算效率高且對小流量水網適應性好的突出優勢。

3）文中所提協同估計和聯合估計均有助于改善電網和水網的狀態估計精度，對電-水耦合環節的數據一致性和耦合網絡的可觀性有一定提升效果。

參考文獻

［ 1 ］ 孫宏斌， 郭慶來， 吳文傳， 等. 面向能源互聯網的多能流綜合能量管理系統： 設計與應用[J]. 電力系統自動化， 2019， 43（12）：122-128， 171.

Sun H B， Guo Q L， Wu W C， et al. Integrated energy management system with multi-energy flow for energy Internet： designand application[J]. Automation of Electric Power Systems， 2019， 43（12）： 122-128， 171. （in Chinese）

［ 2 ］ 臧海祥， 耿明昊， 黃蔓云， 等. 電-熱-氣混聯綜合能源系統狀態估計研究綜述與展望[J]. 電力系統自動化， 2022， 46（7）：187-199.

Zang H X， Geng M H， Huang M Y， et al. Review and prospect of state estimation for electricity-heat-gas integrated energysystem[J]. Automation of Electric Power Systems， 2022， 46（7）： 187-199. （in Chinese）

［ 3 ］ 董今妮， 孫宏斌， 郭慶來， 等. 面向能源互聯網的電-氣耦合網絡狀態估計技術[J]. 電網技術， 2018， 42（2）： 400-408.

Dong J N， Sun H B， Guo Q L， et al. State estimation of combined electric-gas networks for energy Internet[J]. Power SystemTechnology， 2018， 42（2）： 400-408.（in Chinese）

［ 4 ］ Zang H X， Geng M H， Huang M Y， et al. Asynchronous and adaptive state estimation of integrated electricity-gas energysystems[J]. IEEE Internet of Things Journal， 2023， 10（9）： 7636-7644.

［ 5 ］ Xu D L， Xu J J， Wu Z J， et al. A real-time state estimation framework for integrated energy system considering measurementdelay[J]. IET Generation， Transmission & Distribution， 2022， 16（14）： 2891-2902.

［ 6 ］ Zang H X，Geng M H，Xue M F，et al. A robust state estimator for integrated electrical and heating networks[J]. IEEE Access，2019， 7： 109990-110001.

［ 7 ］ Sheng T T， Yin G X， Guo Q L， et al. A hybrid state estimation approach for integrated heat and electricity networks consideringtime-scale characteristics[J]. Journal of Modern Power Systems and Clean Energy， 2020，8（4）： 636-645.

［ 8 ］ 董今妮， 孫宏斌， 郭慶來， 等. 熱電聯合網絡狀態估計[J]. 電網技術， 2016（6）： 1635-1641.

Dong J N， Sun H B， Guo Q L， et al. State estimation for combined electricity and heat networks[J]. Power System Technology，2016（6）： 1635-1641. （in Chinese）

［ 9 ］ Du Y X， Zhang W， Zhang T T. ADMM-based distributed state estimation for integrated energy system[J]. CSEE Journal ofPower and Energy Systems， 2019， 5（2）： 275-283.

［10］ 劉鑫蕊， 李垚， 孫秋野， 等. 基于多時間尺度的電-氣-熱耦合網絡動態狀態估計[J]. 電網技術， 2021， 45（2）： 479-488.

Liu X R， Li Y， Sun Q Y， et al. Interaction and joint state estimation of electric-gas-thermal coupling network[J]. Power SystemTechnology， 2021， 45（2）： 479-488. （in Chinese）

［11］ Xiang X Z， Jia S F. China’s water-energy nexus： assessment of water-related energy use[J]. Resources， Conservation andRecycling， 2019， 144：32-38.

［12］ 趙霞， 孫名軼， 李欣怡， 等. 面向區域綜合能源服務的電-水聯合潮流[J]. 電力自動化設備， 2020， 40（12）： 23-30.

Zhao X， Sun M Y， Li X Y， et al. Combined load flow of integrated electricity-water system for regional multi-energy service[J].Electric Power Automation Equipment， 2020， 40（12）： 23-30. （in Chinese）

［13］ Zamzam A S， Dall'Anese E， Zhao C， et al. Optimal water-power flow problem： formulation and distributed optimal solution[J].IEEE Transactions on Control of Network Systems， 2018，6（1）： 37-47.

［14］ 宋仕恒， 穆云飛， 孟憲君， 等. 面向分布式電源消納的配電網-配水網經濟調度方法[J]. 電力系統自動化， 2019， 43（11）：95-103.

Song R H， Mu Y F， Meng X J， et al. Joint economical dispatch method of power distribution network and water distributionsystem for distributed generator accommodation [J]. Automation of Electric Power Systems， 2019， 43（11）： 95-103. （in Chinese）

［15］ Moazeni F， Khazaei J， Mitra P. An integrated state-estimation framework for interdependent water and energy systems[J].Journal of Hydrology， 2020， 590（125393）.

［16］ Tshehla K S， Hamam Y， Abu-Mahfouz A M. State estimation in water distribution network： a review[C]//2017 IEEE 15thInternational Conference on Industrial Informatics （INDIN）. IEEE， 2017： 1247-1252.

［17］ Sterling M J H， Bargiela A. Minimum norm state estimation for computer control of water distribution systems[J]. IEEProceedings D： Control Theory and Applications， 1984， 131（2）： 57-63.

［18］ Fusco F， Arandia E. State estimation for water distribution networks in the presence of control devices with switching behavior[J]. Procedia Engineering， 2017， 186：592-600.

［19］ Arsene C T C， Gabrys B. Mixed simulation-state estimation of water distribution systems based on a least squares loop flowsstate estimator[J]. Applied Mathematical Modelling， 2014， 38（2）： 599-619.

［20］ Cheng W P， Yu T C， Xu G. Real-time model of a large-scale water distribution system[J]. Procedia Engineering， 2014， 89：457-466.

［21］ Andersen J H， Powell R S. Implicit state-estimation technique for water network monitoring[J]. Urban Water， 2000， 2（2）：123-130.

［22］ Bargiela A. On-line monitoring of water distribution networks[D]. Durham， North East England， UK： Durham University， 1984.

［23］ 陳艷波， 于爾鏗. 電力系統狀態估計[M]. 北京： 科學出版社， 2021.

Chen Y B， Yu E K. Power system state estimation[M]. Beijing： Science Press， 2021.（in Chinese）

［24］ Gomez-Exposito A， Gomez-Quiles C， de la Villa Jaen A. Bilinear power system state estimation[J]. IEEE Transactions onPower Systems， 2012， 27（1）： 493-501.

［25］ Gómez-Quiles C， Gil H A， de la Villa Jaen A， et al. Equality-constrained bilinear state estimation[J]. IEEE Transactions onPower Systems， 2013， 28（2）： 902-910.

［26］ Chen Y B， Ma J， Liu F， et al. A bilinear robust state estimator[J]. International Transactions on Electrical Energy Systems，2016， 26（7）： 1476-1492.

［27］ 陳艷波， 馬進. 一種雙線性抗差狀態估計方法[J]. 電力系統自動化， 2015（6）： 41-47.

Chen Y B， Ma J. A bilinear robust state estimation method for power systems[J]. Automation of Electric Power Systems， 2015，39（6）： 41-47. （in Chinese）

［28］ 鄭順林， 劉進， 陳艷波， 等. 基于加權最小絕對值的電-氣綜合能源系統雙線性抗差狀態估計[J]. 電網技術， 2019， 43（10）：3733-3744.

Zheng S L， Liu J， Chen Y B， et al. Bilinear robust state estimation based on weighted least absolute value for integratedelectricity-gas system [J]. Power System Technology， 2019， 43（10）： 3733-3742. （in Chinese）

［29］ 陳艷波， 姚遠， 楊曉楠， 等. 面向電-熱綜合能源系統的雙線性抗差狀態估計方法[J]. 電力自動化設備， 2019， 39（8）： 47-54.

hfzw7ZcCp7+i5LUY52s5Ig==Chen Y B， Yao Y， Yang X N， et al. Bilinear robust state estimation method for integrated electricity-heat energy systems[J].Electric Power Automation Equipment， 2019， 39（8）：47-54. （in Chinese）

［30］ 嚴煦世， 劉遂慶. 給水排水管網系統[M]. 3 版. 北京： 中國建筑工業出版社， 2014.

Yan X S， Liu S Q. Water supply and drainage network system[M]. 3rd ed. Beijing： China Architecture & Building Press， 2014.（in Chinese）

［31］ Mays L W. Water resources engineering[M]. 2nd ed. Hoboken， NJ： John Wiley & Sons， 2011.

［32］ Rossman L A. EPANET 2 user’s manual[J]. Laboratory Office of Research & Development U. S. Environmental ProtectionAgency， 2000， 19（1）：115-118.

［33］ Abraham E， Stoianov I. Sparse null space algorithms for hydraulic analysis of large-scale water supply networks[J]. Journal ofHydraulic Engineering， 2016， 142（3）： 4015058.1.

［34］ Zimmerman R D， Murillo-Sanchez C E. Matpower 7.1 user’s manual[J]. Power Systems Engineering Research Center， 2011.

［35］ Cui J X. 11 node WDN[EB/OL][2023-02-21]. https：//www.researchgate.net/publication/368667053_11nodeWDN.

（編輯 詹燕平）