混合儲能系統快速功率響應模型預測控制

摘 要：

針對混合儲能系統平抑微電網大功率負荷突變引起的直流母線電壓波動過程中控制響應速度慢、儲能功率分配不合理等問題，提出混合儲能系統快速功率響應模型預測控制。首先，根據儲能系統預測電流值與系統功率補償量得到儲能系統預測功率并將其作為參考功率，設計基于有理函數擬合的功率配置方案對參考功率進行優化配置，得到鋰電儲能與飛輪儲能的參考功率，實現飛輪儲能系統容量的最大化利用，減少突變功率對電池影響，延長電池使用壽命。其次，通過儲能系統功率電流變換關系獲得參考電流值，并采用增量式模型預測控制算法對鋰電-飛輪儲能系統進行控制，得到最優控制輸出，使實際電流快速跟隨參考電流以抑制直流母線電壓波動。最后，通過仿真和硬件在環半實物仿真驗證所提控制策略的有效性及實用性。

關鍵詞：混合儲能系統；負荷突變；功率預測；有理函數擬合；功率配置；增量式模型預測控制

DOI：10.15938/j.emc.2024.09.003

中圖分類號：TM46

文獻標志碼：A

文章編號：1007-449X（2024）09-0022-14

收稿日期： 2024-06-17

基金項目：國家自然科學基金（52177211）；國家自然科學基金（52201396）

作者簡介：佀 想（2000—），男，碩士研究生，研究方向為混合儲能系統快速功率控制;

段建東（1985—），男，博士，教授，博士生導師，研究方向為新能源發電與電儲能、微網能量變換與協調控制等；

王露霄（1996—），男，博士研究生，研究方向為船舶微電網能量管理；

徐一明（1999—），男，碩士研究生，研究方向為飛輪儲能高速永磁同步電機控制；

趙 克（1973—），男，博士，副教授，研究方向為交流永磁電機控制與驅動、大功率能量變換系統等。

通信作者：段建東

Fast-power-response model predictive control for hybrid energy storage systems

SI Xiang1， DUAN Jiandong1，2， WANG Luxiao1， XU Yiming1， ZHAO Ke1

（1.School of Electrical Engineering and Automation， Harbin Institute of Technology， Harbin 150001， China；2.State Key Laboratory of Hydro-Power Equipment， Harbin 150001， China）

Abstract：

In order to address issues such as slow control response speed and unreasonable energy storage power distribution in the process of hybrid energy storage system stabilizing DC bus voltage fluctuation caused by high-power load mutation of microgrid， a fast power response model predictive control for hybrid energy storage systems was proposed. Firstly， according to the predicted current value of the energy storage system and the system power compensation amount， the predicted power of the energy storage system was obtained and used as the reference power. The power configuration scheme based on rational function fitting was designed to optimize the reference power to obtain the reference power of lithium battery energy storage and flywheel energy storage. In the method， the maximum utilization of the capacity of the flywheel energy storage system was realized， and the influence of the sudden power was reduced on the battery and prolongs the service life of the battery. Secondly， the reference current value was obtained through the power-current transformation relationship of the energy storage system， and the incremental model predictive control algorithm was used to unify the control of the lithium-flywheel energy storage system to obtain the optimal control output， ensuring that the actual current quickly follows the reference current to suppress DC bus voltage fluctuations. Finally， effectiveness and practicability of the proposed control strategy are verified by simulation and hardware-in-the-loop semi-physical simulation.

Keywords：hybrid energy storage system; load mutation; power prediction; rational function fitting; power allocation; incremental model predictive control

0 引 言

微電網電壓波動可以采用儲能系統進行抑制［1-2］。儲能系統可分為功率型儲能和能量型儲能。能量型儲能能量密度高，可以長時間放電，但功率密度低；功率型儲能功率密度高，能實現快速充放電，但能量密度低。將二者結合起來構成混合儲能系統，克服單一儲能的缺點以提升微電網性能［3-5］。

目前混合儲能系統（hybrid energy storage system，HESS）抑制電壓波動的控制方法以雙比例積分（proportional integral，PI）控制為主。文獻［6］將PI控制器產生的HESS電流參考值轉化為正的下降信號，補償動態電壓誤差，使動態電壓穩定收斂于期望值，避免了過沖現象。文獻［7］提出一種PI和滑模技術相結合的控制技術，以改善蓄電池和超級電容之間的均流，從而減小需求功率與發電功率間的差距，調節直流母線電壓。文獻［8］提出變增益比例控制策略，根據母線電壓與空載電壓偏移量調整比例增益，抑制電壓外環超調過大。文獻［9］提出一種無差拍控制方法，可以在一個控制周期內產生最優占空比，具有更快的響應速度。文獻［10］提出一種基于強化學習的電流控制策略，在系統參數未知的微電網中控制HESS平滑地進行充放電，避免了微電網中不規范充放電引起的擾動。文獻［11］設計了模型預測電流控制及模型預測功率控制方案，該方案避免了PI的參數整定、PWM調制和復雜的坐標變換，但此方案采用多個模型預測部分，增加了運算的復雜程度，耗費時間長。文獻［12］提出一種基于實時非線性模型預測的混合儲能系統控制策略，通過補償線性模型預測控制中線性化伴隨的誤差，實現更優的控制性能。文獻［13］設計超螺旋滑模控制器維持系統功率平衡，進而抑制直流母線電壓波動。文獻［14］提出自適應模糊比例積分微分控制器，該控制器以較小的電池應力抑制直流母線電壓波動，提高電池的使用時間。

為了充分利用儲能系統能量，需要進行功率配置設計。文獻［15］將用于解耦平均和暫態的低通濾波器替換為單一的倍率限制器，但是單一的倍率控制器的斜率設計是一大難點，需要考慮如何最大化儲能的利用率。文獻［16］提出一種基于不同儲能系統之間功率共享的能量管理方案，具有更快的電壓調節速度以應對負荷擾動，降低瞬態功率波動期間電池電流的充電/放電率，延長電池使用壽命。文獻［17］提出的控制策略引入充放電閾值優化功率分配的方法，采用最優化算法不斷修正閾值系數，實現功率的優化分配。文獻［18-19］提出的HESS控制器利用超級電容電壓的低頻分量來產生電池參考電流，為電池分配低頻功率的同時將電池電流和超級電容電壓維持在預定的范圍內。文獻［20］提出一種基于儲能單元荷電狀態（state of charge，SOC）與累計放電量的正比關系進行功率分配的方法，沒有綜合考慮儲能不同階段SOC的特性，儲能系統利用率低。文獻［21］將功率需求分解為本征模態函數分量并重構為高低頻分量分配給鋰電池和超級電容，有效地降低電池的最大放電電流。文獻［22］通過優化梯度算法對高頻和中頻的參考功率進行二次優化，平抑風電功率波動，提高混合儲能系統利用率。

針對微電網中混合儲能系統功率配置與電壓波動抑制的問題，本文提出混合儲能系統快速功率響應模型預測控制。首先，根據儲能系統預測電流值與系統功率補償量得到儲能系統預測功率并作為參考功率，設計基于有理函數擬合的功率配置方案對參考功率進行優化配置，得到鋰電儲能與飛輪儲能的參考功率，實現飛輪儲能系統容量的最大化利用，減少突變功率對電池影響，延長電池使用壽命。其次，通過儲能系統功率電流變換關系獲得參考電流值，并采用增量式模型預測控制（incremental model predictive control considering optimal power allocation，IMPC）算法對鋰電-飛輪儲能系統統一控制，得到最優控制輸出，使實際電流快速跟隨參考電流以抑制直流母線電壓波動。所提控制策略具有一定的通用性，體現在其能夠根據不同儲能系統數學模型設計功率預測控制及IMPC，使儲能系統快速輸出期望功率，提高儲能系統的動態性能。最后，通過仿真和實驗驗證所提控制策略的有效性及實用性。

1 系統建模與控制

1.1 儲能數學建模

微電網系統框圖如圖1所示，其構成包括發電機、AC/DC變換器、DC/AC變換器、DC/DC變換器、直流負載、交流負載及HESS，HESS包括鋰電儲能系統及飛輪儲能系統。

鋰電儲能系統拓撲如圖2所示，主要由鋰電池和DC/DC變換器組成。其中：C1、C為穩壓電容；S1、S2為IGBT；LB為穩流電感；iB為電感電流；Vin為輸入電壓；Vdc為輸出電壓；iB1為鋰電儲能系統輸出電流；ic為直流母線電容吸收電流。

為了研究鋰電儲能系統的控制策略，需要獲得鋰電儲能系統的數學模型［23-24］，可以得到不同開關狀態下對應的數學模型為：

S2=1，S1=0∶Vin=LBdiBdt+Vdc；

S2=0，S1=1∶Vin=LBdiBdt。（1）

由式（1）得到鋰電儲能系統DC/DC變換器一個開關周期內對應的數學模型為

LBdiBdt=Vin－Vdc（1－d）。（2）

式中d為開關占空比。

飛輪儲能系統主要由雙向DC/AC變換器、永磁同步電機和飛輪組成，飛輪儲能系統拓撲如圖3所示。其中：Pe是永磁同步電機電磁功率；Pf是飛輪儲能系統輸出功率；if是飛輪儲能系統輸出電流；ua、ub、uc是永磁同步電機端電壓。

飛輪儲能系統在d-q軸的電氣模型［25-26］為：

vd=Rsid+ddtλd－ωeλq ；

vq=Rsiq+ddtλq+ωeλd；

λd=Ldid+λf；

λq=Lqiq。（3）

式中：vd和vq是定子電壓；id和iq是定子電流；變量ωe、Rs和λf分別是電角速度、定子電阻和電機磁鏈；Ld和Lq是定子電感。由式（3）得到飛輪儲能系統的狀態空間方程為

ddtidiq=－RsLdωeLqLd－ωeLdLq－RsLqidiq+

1Ld001Lqvdvq+0－ωeλfLq。（4）

永磁同步電機功率控制模型可以表示為：

Pe=32pλfiqωm；

Pf=Pe+ΔPf。（5）

式中：ωm為永磁同步電機機械轉速；ΔPf為飛輪儲能系統機械損耗及電阻損耗。

1.2 系統控制目標及約束

直流微電網系統面對大功率負荷突變時，母線電壓會發生波動。混合儲能系統的加入能夠抑制直流母線電壓的波動。當大功率負荷突變時，微電網系統的功率流動方向如圖4所示。其中：PHESS為儲能系統需要釋放或吸收的功率；Pload為負荷功率。不良的控制策略使得HESS功率響應慢，導致母線電壓波動。其次，儲能功率的不合理配置不能充分發揮HESS的作用。

基于上述問題設計HESS控制策略。首先要使HESS輸出功率快速跟隨負荷功率，其次要合理利用混合儲能系統能量，提高儲能系統利用率。系統的控制目標及約束可表示為：

Min Vdcref－Vdc；（6）

PBmin≤PB≤PBmax；（7）

P·Bmin≤P·B≤P·Bmax；（8）

Pfmin≤Pf≤Pfmax。（9）

式（6）給出了最小化母線電壓波動的控制目標，以母線電壓波動量及電壓恢復時間反應功率響應速度；式（7）給出了鋰電儲能系統輸出功率幅值的約束；式（8）給出了鋰電池儲能系統輸出功率變化率的約束；式（9）給出了飛輪儲能系統輸出功率大小的約束。

根據上述目標約束條件設計混合儲能系統快速功率響應模型預測控制，解決HESS功率響應慢、功率分配不合理及系統動態響應差的問題。

2 功率預測及配置方案

混合儲能系統快速功率響應模型預測控制框圖如圖5所示。

所提控制方法通過功率預測獲得參考功率值，參考功率值經功率配置得到鋰電儲能系統及飛輪儲能系統參考功率，進一步通過功率電流關系獲得電流參考值。將電流參考值代入混合儲能系統數學模型中，并通過IMPC獲得控制輸出。最后，經過PWM/SVPWM模塊得到開關狀態，控制變換器輸出相應功率。

2.1 功率預測

根據圖1所示的微電網結構框圖可以得到直流微電網系統的功率平衡關系為

PHESS=Pload1+Pload2+…+Ploadn+Pg。（10）

式中Pg為發電機經AC/DC變換器向直流母線提供的功率。

混合儲能系統的功率分配關系可表示為

PHESS=PB+Pf。（11）

式中PB為鋰電輸出功率。根據HESS功率分配關系可進一步得到HESS電流分配關系為：

iHESS（t）=ic（t）+iload（t）；

iHESS（t）=iB1（t）+if（t）。（12）

式中iload為負載電流。根據式（12）負載電流觀測值可以表示為

i^load（t）=iHESS（t）－ic（t）。（13）

忽略飛輪儲能系統的機械損耗及電阻損耗，飛輪儲能系統電磁功率與輸出功率間的關系為

Vdcif=1.5pλfωm。（14）

由式（12）～式（14）得到負載電流的觀測模型為

i^load（t）=iB1（t）+if（t）－ic（t）=iB（t）（1－d）+

1.5pλfiq（t）Vdc（t）－CdVdc（t）dt。（15）

由于上式存在微分環節，會放大系統的噪聲，設計截止頻率為200 Hz以濾除系統的高頻噪聲，負載觀測器在頻域的表達式為

i^load（s）=［iB（s）（1－d）+1.5pλfiq（s）Vdc（s）－sCVdc（s）］ωs+ω。（16）

對式（16）進行歐拉離散可得到iload（k）。進一步對母線電容電流進行分析，對于一個確定的電容，其電流電壓關系可以表示為

ic=CdVdcdt。（17）

由此可知，ic的變化會引起直流母線電壓的變化，因此直流母線電壓會在期望值附近波動，并存在偏差。假設短時間內偏差服從線性變化，如圖6所示。

由于消除母線電壓偏差的ic值并非無窮大，故而引入預測區間N預測母線電壓值達到期望值所需的離散時間。當前時刻直流母線電壓可能比期望母線電壓值高或低，因此需要通過減小或增大ic使直流母線電壓達到期望。N表示母線電壓將在N步之內達到期望電壓值，考慮k+1時刻母線電壓值可以得到

Vdc（k）－Vdc（k+1）1=Vdc（k）－V*dcN。（18）

式中V*dc為母線電壓期望值。進一步得到

Vdc（k+1）=Vdc（k）+1N［V*dc－Vdc（k）］。（19）

對式（17）離散化，得到第k+1步母線電容電流為

ic（k+1）=CT［Vdc（k+1）－Vdc（k）］=

CNT［V*dc－Vdc（k）］。（20）

式中N為整數，用于限制電容電流。根據式（12），第k+1步混合儲能系統預測電流值可以表示為

iHESS（k+1）=i^load（k+1）+ic（k+1）=

i^load（k）+Δi+ic（k+1）。（21）

式中Δi為一個離散周期內，由負荷突變帶來的負荷電流變化量。穩態狀況下，第k+1步混合儲能預測電流值可表示為

iHESS（k+1）=i^load（k）+ic（k+1）。（22）

根據直流系統電流功率變換關系，第k+1步混合儲能系統預測功率為

P*HESS（k+1）=V*dciHESS（k+1）。（23）

P*HESS（k+1）是在理想、無損耗的情況下得到的，而在實際情況下系統會產生損耗，使系統輸出功率產生偏移，其次在非穩態狀況下，系統將產生Δi，使母線電壓偏離參考值，因此采用PI控制獲得功率補償，消除由突變功率及系統損耗引起的電壓偏差，得到最終的參考功率值為

PHref=P*HESS+ΔP。（24）

其中

ΔP=［kpz+kiz（V*dc－Vdc）］V*dc。（25）

2.2 功率配置

根據儲能系統特性，飛輪儲能系統提供高頻功率波動分量，鋰電儲能系統提供低頻功率波動分量。采用一階低通濾波器，分離功率波動中的高低頻分量，可表示為：

PL=PHrefωrs+ωr；

PH=PHref（1－ωrs+ωr）。（26）

式中：PL為低頻功率分量；PH為高頻功率分量；ωr為低通濾波器截止頻率。

為了充分利用飛輪儲能系統快速功率響應特性，并減緩快速的負荷沖擊對鋰電儲能系統的影響，進一步對低頻功率分量進行設計。當大功率負荷突變時，飛輪儲能系統承擔全部的功率沖擊，并逐步減小出功，由鋰電儲能系統承擔全部負載功率。采用速率限制器分離低頻分量中的突變分量并滿足式（8）的要求。當鋰電儲能系統功率變化率超過最大變化率時，輸出功率可表示為：

Psm（k+1）=PL（k）+FT；

Pbr（k+1）=PL（k+1）－Psm（k+1）。（27）

式中：Pbr為突變分量；Psm為慢變分量；F為最大變化率；T為離散時間。

考慮儲能系統輸出功率與儲能容量之間的關系并基于式（7）和式（9）的約束，設計基于有理數擬合的閾值分配方案來優化儲能系統之間的功率分配。

鋰電儲能系統及飛輪儲能系統正常運行時的容量范圍為：

20%SOCLimax≤SOCLi≤80%SOCLimax；

5%SOCfmax≤SOCf≤95%SOCfmax 。

（28）

首先建立飛輪儲能系統容量與輸出功率邊界之間的關系，假定存在變換因子a和b，變換因子由下式決定：

P-fmax=aPfmax；

P-fmin=bPfmin。（29）

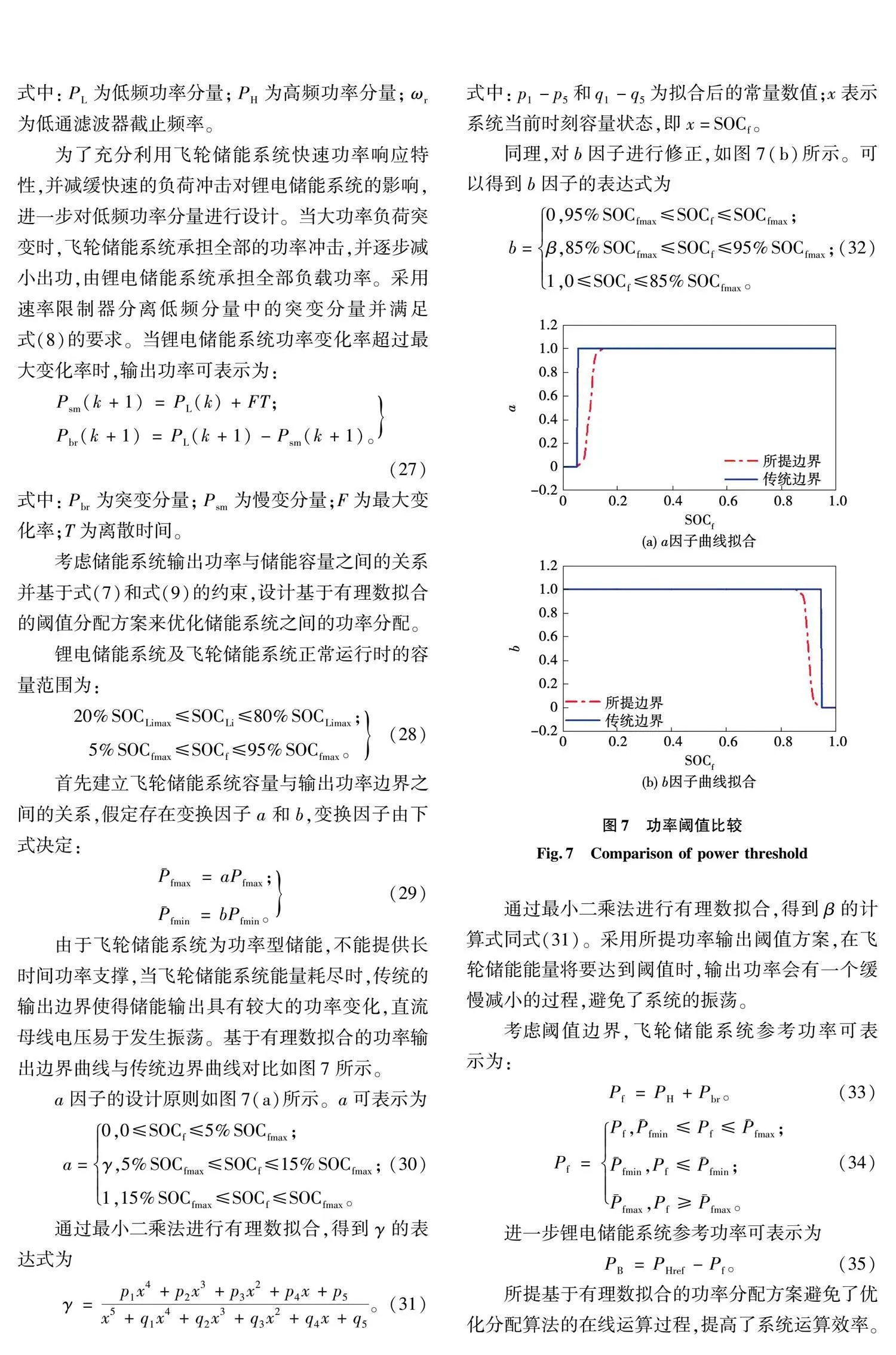
由于飛輪儲能系統為功率型儲能，不能提供長時間功率支撐，當飛輪儲能系統能量耗盡時，傳統的輸出邊界使得儲能輸出具有較大的功率變化，直流母線電壓易于發生振蕩。基于有理數擬合的功率輸出邊界曲線與傳統邊界曲線對比如圖7所示。

a因子的設計原則如圖7（a）所示。a可表示為

a=0，0≤SOCf≤5%SOCfmax；

γ，5%SOCfmax≤SOCf≤15%SOCfmax；

1，15%SOCfmax≤SOCf≤SOCfmax。（30）

通過最小二乘法進行有理數擬合，得到γ的表達式為

γ=p1x4+p2x3+p3x2+p4x+p5x5+q1x4+q2x3+q3x2+q4x+q5。（31）

式中：p1－p5和q1－q5為擬合后的常量數值；x表示系統當前時刻容量狀態，即x=SOCf。

同理，對b因子進行修正，如圖7（b）所示。可以得到b因子的表達式為

b=0，95%SOCfmax≤SOCf≤SOCfmax；

β，85%SOCfmax≤SOCf≤95%SOCfmax；

1，0≤SOCf≤85%SOCfmax。（32）

通過最小二乘法進行有理數擬合，得到β的計算式同式（31）。采用所提功率輸出閾值方案，在飛輪儲能能量將要達到閾值時，輸出功率會有一個緩慢減小的過程，避免了系統的振蕩。

考慮閾值邊界，飛輪儲能系統參考功率可表示為：

Pf=PH+Pbr。（33）

Pf=Pf，P-fmin≤Pf≤P-fmax；

P-fmin，Pf≤P-fmin；

P-fmax，Pf≥P-fmax。（34）

進一步鋰電儲能系統參考功率可表示為

PB=PHref－Pf。（35）

所提基于有理數擬合的功率分配方案避免了優化分配算法的在線運算過程，提高了系統運算效率。

3 增量式模型預測電流控制方案

永磁同步電機采用id=0控制方式并通過控制q軸電流輸出功率。根據鋰電儲能功率電流關系及式（5）獲得儲能系統參考電流值為：

iBref=PB/Vdc；

iqref=Pf/（1.5pλfωm）。（36）

設計增量式模型預測控制電流環以控制混合儲能系統輸出電流跟隨參考電流，其思路是首先得到鋰電-飛輪混合儲能系統的統一化離散數學模型；其次設計基于增量式控制算法；最后設計模型預測控制代價函數，得到最優控制輸出。

3.1 模型預測控制策略設計

設混合儲能系統參考電流為

iref（k）=iBref（k）idref（k）iqref（k）。（37）

由于混合儲能系統電流參考值是非穩定值且是非線性變化的，為此需要建立離散期望電流之間的聯系。構建目標轉移矩陣方程為

iref（k+1）=ADiref（k）。（38）

式中AD為轉移矩陣。對式（2）進行離散化，得到鋰電儲能系統離散模型為

iB（k+1）=iB（k）+TL{Vin－Vdc［1－d（k）］}。（39）

式中T為離散周期。定義鋰電儲能系統控制量為

uB（k）=TL{Vin－Vdc［1－d（k）］}。（40）

對式（4）進行離散化，得到飛輪儲能系統離散模型為

id（k+1）iq（k+1）=1－RsTLωeT－ωeT1－RsTLid（k）iq（k）+

1001ud（k）uq（k）。（41）

其中飛輪儲能系統控制量表示為：

ud（k）=vd（k）TL；

uq（k）=vq（k）TL－ωeλfTL。（42）

以控制增量作為優化目標設計控制策略，控制增量可以表示為

Δu（k）=u（k）－u（k－1）。（43）

式中u（k）為系統k時刻控制量。其表達式為

u（k）=uB（k）ud（k）uq（k）。（44）

進一步得到混合儲能系統離散模型為

i（k+1）=Ai（k）+Bu（k）=Ai（k）+BΔu（k）+Bu（k－1）。（45）

其中：

i（k）=iB（k）id（k）iq（k）； A=10001－TRsLTωe0－Tωe1－TRsL；

B=100010001。

設增廣矩陣為

ia（k）=i（k）iref（k）u（k－1），（46）

得到誤差變量與增廣矩陣之間的關系為

e（k）=i（k）－iref（k）=［I－I0］i（k）iref（k）u（k－1）。（47）

式中e（k）為第k步誤差變量。增廣矩陣與控制增量之間的離散化矩陣模型為

ia（k+1）=i（k+1）iref（k+1）u（k）=

A0B0AD000Ii（k）iref（k）u（k－1）+B0IΔu（k）。（48）

考慮系統的終端誤差、誤差及控制增量之間的優化關系，設置模型預測控制代價函數為

J=12eT（N）Se（N）+12∑N－1k=0（eT（k）Qe（k）+ΔuT（k）RΔu（k））。（49）

其中：

S=s000s000s；Q=q000q000q；R=r000r000r。

式中S、Q、R分別表示終端誤差權重系數、誤差權重系數、控制增量權重系數。

根據式（47）和式（49）得到表征增廣矩陣與控制增量之間優化關系的代價函數為

J=12iTa（N）Saia（N）+12∑N－1k=0（iTa（k）Qaia（k）+

ΔuT（k）RΔu（k））。（50）

其中：

Sa=［I－I0］TS［I－I0］；

Qa=［I－I0］TQ［I－I0］。（51）

通過調整權重系數使系統電流誤差最小。所提IMPC策略采用無約束解析法對代價函數做最優化運算，并對優化結果設計硬約束限制，表達式為

umin≤u（k）≤umax。（52）

得到變換器控制增量最優值后，通過式（40）、式（42）及式（43）得到最優控制量，控制開關管通斷，使儲能系統輸出參考電流，響應功率變化。

IMPC狀態變量的實時反饋使得控制器能夠及時響應系統的變化，避免外界干擾對系統的影響，提高控制系統的穩定性。其次，所提控制策略以控制增量設計代價函數，避免了傳統以控制量設計代價函數所引起的穩態誤差問題，具有更優的控制性能。IMPC總體框圖如圖8所示。

3.2 電流期望值補償

由于鋰電儲能系統實際電流在一個周期內存在一個充放電過程，電流值并非是恒定值。假設電流的返回值iB（k）是一個周期內電感釋放能量后的值，設此時的電流期望值為i′Bref，一個周期內電流跟隨情況如圖9（a）所示。

在一個周期內，電感電流可以視為線性變化的，需要在電感電流上升過程的中點處給出預測值，如圖9（b）所示，故需要對電流期望值進行補償。令補償的電流值為Δid，補償后的電流期望值為

iBref=i′Bref+Δid。（53）

式中iBref為補償后的電流期望值。根據電感電流一個周期內上升尺度與時間關系，電流補償量大小為

Δid=－VinTd2LB。（54）

所提增量式模型預測控制算法對混合儲能系統統一控制，能夠實時響應混合儲能系統狀態變量的變化，使實際輸出電流快速跟隨參考電流值，提高儲能系統電流的響應速度。

3.3 參數設計

由于功率控制部分引入PI功率補償及電流濾波環節，因此需要考慮PI控制參數設計問題，以提高系統的穩定性及快速性。在傳統雙PI控制下，需要考慮兩個PI控制器之間的帶寬匹配問題。所提控制策略電流內環采用IMPC，避免了內環控制器對外環控制器的影響。

以鋰電儲能系統為例，說明PI控制參數的設計過程。鋰電儲能系統的控制框圖如圖10所示。其中：GLpi為PI控制器；Gω為低通濾波器；GLi_v為鋰電儲能系統輸出電壓到輸出電流間的傳遞函數；Gτ為延時函數；GLd_i為鋰電儲能系統輸出電流到占空比之間的傳遞函數。

鋰電儲能系統DC/DC變換器小信號模型為

ddti^Bv^dc=0－（1－D）LB－（1－D）C－1CRLi^Bv^dc+VdcLB－IBCd^。（55）

式中：D為穩態時刻系統占空比；RL為負載電阻。s域下的矩陣模型可表示為

s1－DLB－（1－D）Cs+1CRLi^B（s）v^dc（s）=VdcLB－IBCd^（s）。（56）

進一步，輸出電壓與電感電流間的傳遞函數可以表示為

GLi_v（s）=v^dc（s）i^B（s）=（1－D）vdc－LBIBs（CVdc）s+2（1－D）IB。（57）

由于設計的IMPC的電流跟隨性能優異，通過調整代價函數權重矩陣，可使其動態響應過程可近似為一階慣性系統，對應開環傳遞函數為

GI=1τs+1。（58）

綜上，鋰電儲能系統對應開環傳遞函數為

Gop=GLpiGωGIGLi_v。（59）

加入PI控制后設置穿越頻率為1 500 rad/s，以濾除系統的高頻干擾，設置PI控制器的轉折頻率為原系統轉折頻率的1/30，保證系統留有足夠的相角裕度。經計算可得kp=4.068 4、ki=203.418 8。加入PI系統后的控制系統伯德圖如圖11所示。其中，系統幅值裕度Gm=15.5 dB，相角裕度Pm=52.9°，故系統穩定。

4 仿真與實驗

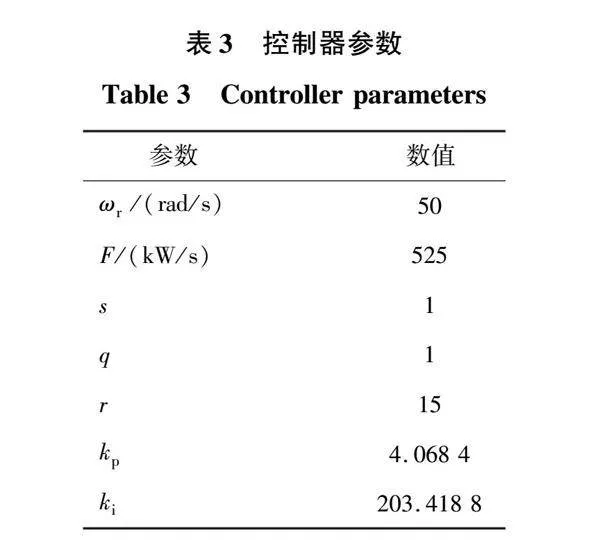
為驗證所提控制策略的有效性，在仿真軟件及半實物仿真平臺RT_BOX中建立如圖1所示微電網系統直流環節。鋰電儲能系統參數配置如表1所示，飛輪儲能系統參數配置如表2所示，控制器參數如表3所示。

基于上述參數配置，將基于IMPC的快速功率控制（fast power control based on incremental model prediction，IMPC_FPC）、基于模型預測的快速功率控制（fast power control based on model prediction，MPC_FPC）和傳統電壓電流雙PI控制（PI_PI）相比較，驗證所提控制策略的合理性和優越性。

4.1 仿真驗證

在MATLAB/Simulink中搭建如圖1所示硬件電路及圖5所示控制算法，驗證所提控制策略有效性。

4.1.1 穩壓性能驗證

設置功率負載需求為100 kW，比較不同控制策略下母線電壓的穩態輸出波動，驗證所提控制策略的穩壓性能。圖12顯示了IMPC_FPC、MPC_FPC和PI_PI方法下鋰電儲能系統的穩壓仿真過程。

IMPC_FPC策略下電壓波動約為0.23 V，MPC_FPC策略下電壓波動約為0.34 V，PI_PI下電壓波動約為0.4 V。經仿真驗證，IMPC_FPC具有更優的穩壓效果。

4.1.2 功率配置方案驗證

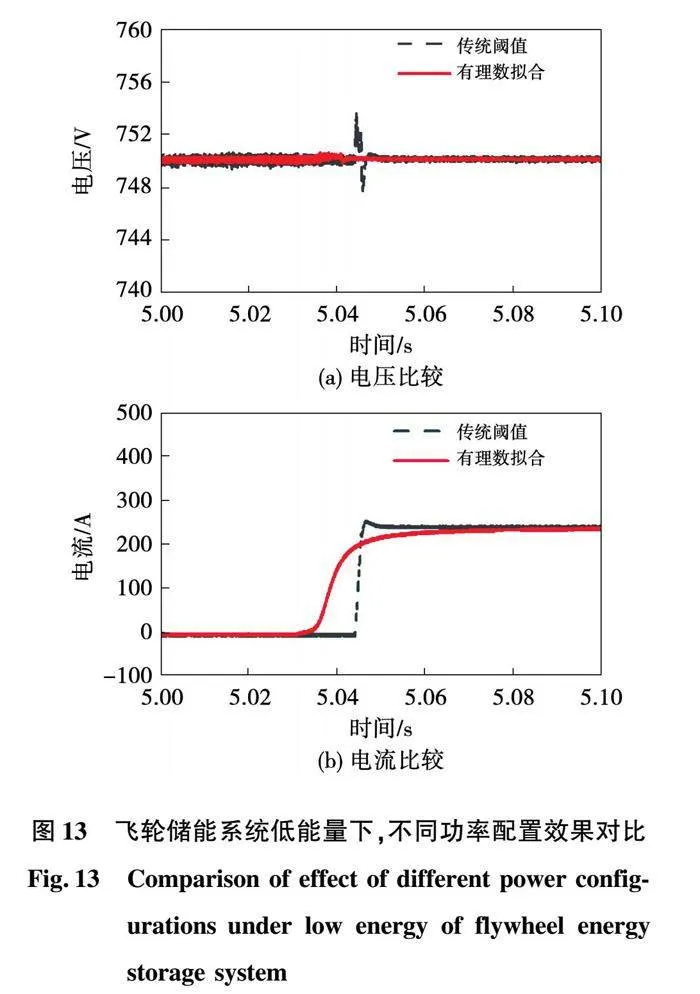
為了驗證基于有理數擬合的功率閾值分配方案，在系統中突加180 kW的大功率負載。首先，由飛輪儲能系統與鋰電儲能系統同時為負荷提供能量，當飛輪儲能系統達到能量閾值時，切換為鋰電儲能系統為負載供電。圖13顯示了基于有理數擬合的容量閾值設計方案及傳統容量閾值設計方案的仿真結果。

圖13（a）為直流母線電壓波形。仿真結果顯示，所提功率分配模式下母線電壓波動約為0.5 V，而傳統閾值設計方式下，母線電壓波動約4.5 V。

圖13（b）為鋰電儲能系統輸出電流波形，所提控制方式下，電流有約25 ms的緩沖時間，而傳統控制方法下僅有5 ms左右的緩沖時間。經仿真驗證，所提控制方法電流上升緩慢，對電池的沖擊小。

4.2 硬件在環半實物仿真驗證

為驗證所提控制策略的動態性能，分別對負載突增和負載突卸工況進行硬件在環半實物仿真實驗。圖14為搭建的實驗平臺，包括RT-BOX3、模擬I/O、數字I/O、F28379D LaunchPad和PLESC軟件平臺。

為充分說明所提控制策略的優越性，將選取以下性能指標進行分析：最大電壓突變量ΔV；電壓恢復過程中的最大量波動ΔVb；電壓恢復時間tr；飛輪儲能系統最大輸出電流If；鋰電儲能系統緩沖時間ts。

4.2.1 電流動態響應性能驗證

為驗證所提控制策略的電流動態響應性能，設置3種控制策略進行性能對比：基于濾波器的PI_PI控制、基于所提功率配置的MPC_FPC與IMPC_FPC策略。

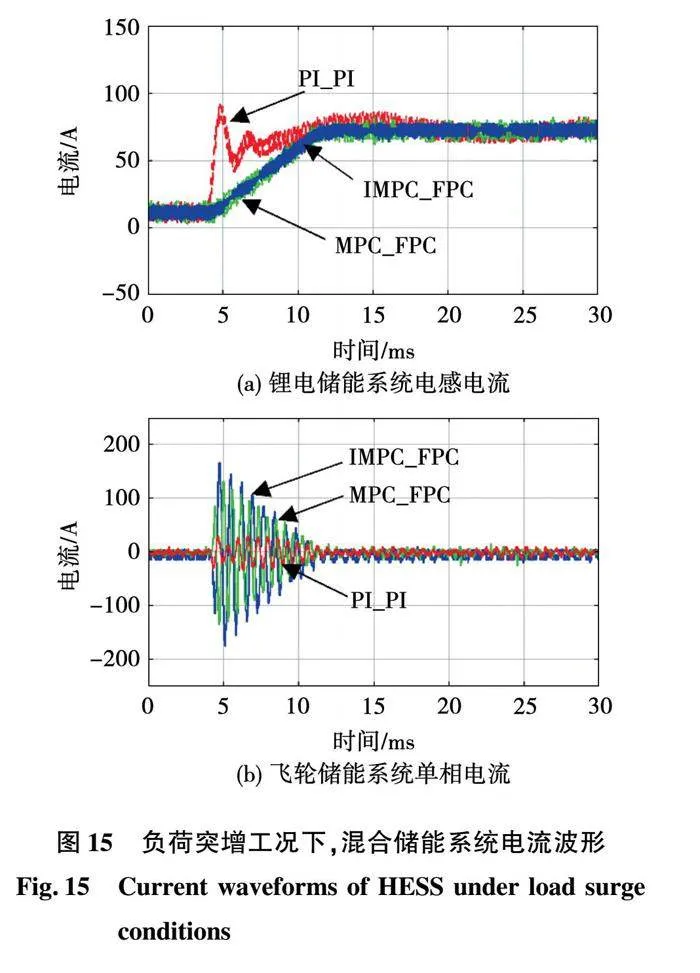
在t=4.5 ms時，突加負荷。圖15為負荷突增工況下，混合儲能系統電流波形。

圖15（a）為負載突增時的鋰電儲能系統電感電流。PI_PI控制過程中鋰電儲能輸出電流在2 ms內從10 A突變至85 A，且發生振蕩過程，對電池沖擊大；MPC_FPC策略下鋰電輸出電流從10 A到75 A，響應時間約7 ms，減小了突變電流對系統的損耗。IMPC_FPC策略下鋰電輸出電流從10 A到75 A，響應時間約7 ms，穩態電流波動更小。實驗結果表明，采用所提控制策略電池電流上升緩慢，電流波動小，對電池沖擊小，延長了電池使用壽命。

圖15（b）為飛輪儲能系統單相電流波形。從圖中可以看出，在負荷突變瞬間，IMPC_FPC策略下最大輸出電流165 A，MPC_FPC策略下最大輸出電流130 A，PI_PI控制下最大輸出電流30 A。實驗結果表明，采用所提功率配置方案飛輪儲能系統能夠快速響應負荷功率變化，提高飛輪儲能系統利用率。

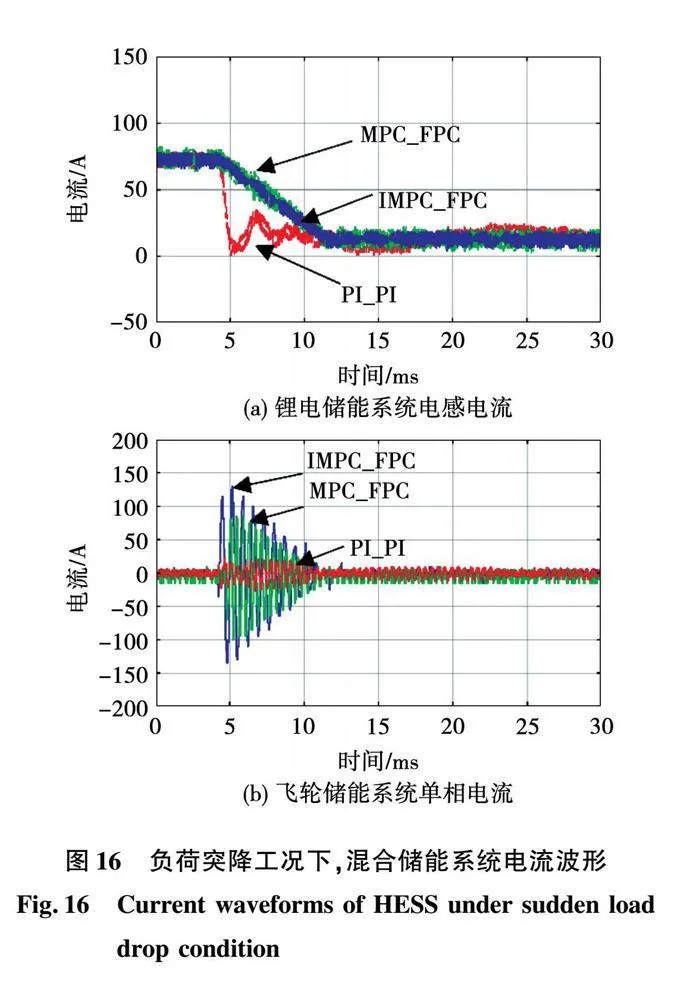
在t=4.5 ms時，突卸負荷。圖16為負荷突卸工況下，混合儲能系統電流波形。

圖16（a）為負載突卸時的鋰電儲能系統電感電流。PI_PI控制下，鋰電系統在1.5 ms內電流從70 A突降至5 A，且發生振蕩過程，對電池沖擊大；MPC_FPC策略下，鋰電儲能在8 ms之內從70 A降至10 A，無振蕩過程；IMPC_FPC策略下，鋰電儲能在8 ms之內從70 A降至10 A，無振蕩過程且電流波動更小。

圖16（b）為飛輪儲能系統單相電流波形。從圖中可以看出：在負荷突卸瞬間，IMPC_FPC策略下最大輸出電流130 A；MPC_FPC策略下最大輸出電流85 A；PI_PI控制下最大輸出電流30 A。實驗結果表明，采用所提功率配置方案，飛輪儲能系統能夠快速響應負荷功率變化，提高飛輪儲能系統的利用率。

不同功率配置下，控制性能對比如表4所示。

由對比結果可知，基于所提功率配置方案的IMPC_FPC策略在面對大功率負荷突變時，飛輪儲能系統能夠承擔突變功率波動，延長鋰電儲能系統的緩沖時間，極大地減少沖擊負荷對電池的影響，提高儲能系統的壽命；其次，所提控制策略電流波動更小，動態響應性能更優。

4.2.2 功率響應性能驗證

為進一步驗證所提功率預測算法優越性，在上述3種控制策略基礎上增加基于模型預測的自適應模糊功率控制（adaptive fuzzy power control based on model prediction，MPC_AFPC）。

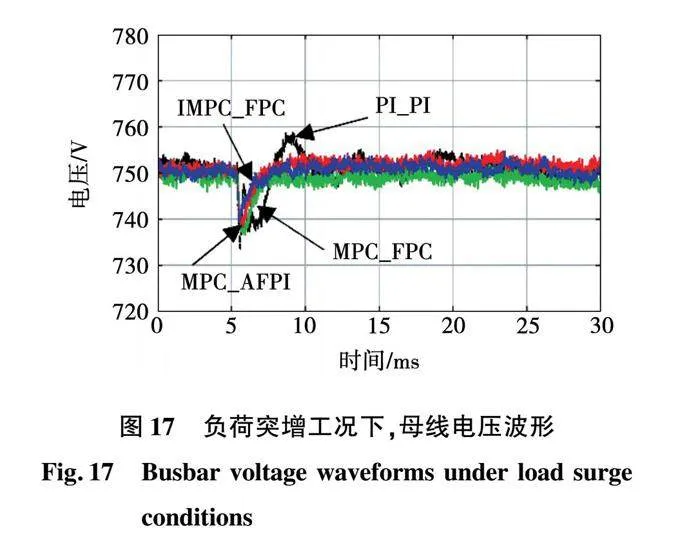
在t=5.5 ms時，突加負荷，圖17為負荷突增下直流母線電壓波形。由實驗結果可知，傳統PI_PI控制下，直流母線電壓跌落至733.6 V。電壓恢復過程中，產生了振蕩及超調，最大波動量約8.79 V。電壓恢復過程耗時長，約為20 ms。MPC_AFPI策略下，電壓跌落至738.25 V，電壓恢復時間約3.2 ms。MPC_FPC策略下，電壓跌落至737.2 V，電壓恢復時間約3.3 ms。IMPC_FPC電壓跌落至739.4 V，在電壓恢復過程中，系統并未產生振蕩及超調，恢復時間約為3.2 ms。

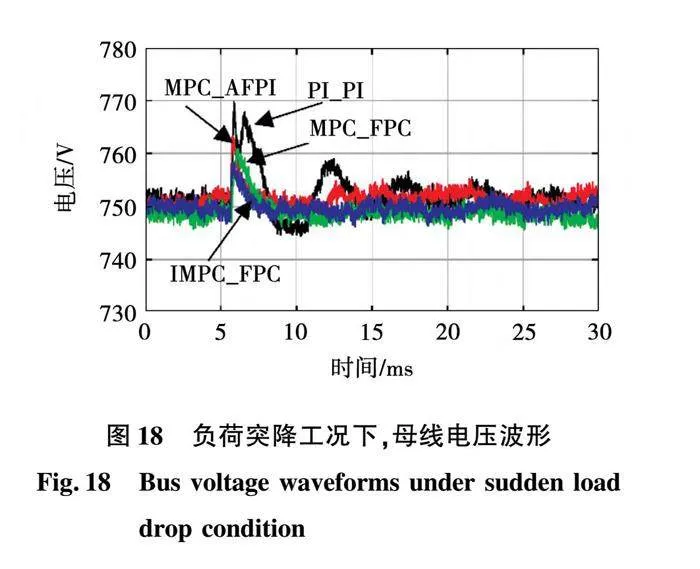
在t=5.5 ms時，突卸負荷，圖18為負荷突卸時直流母線電壓波形。傳統PI_PI控制下，母線電壓突變至769.9 V。在電壓恢復過程中，電壓發生了振蕩并產生了超調，最大波動量約5 V，恢復時間約為25 ms。MPC_AFPI策略下，母線電壓突變至763.4 V，電壓恢復時間約3.1 ms。MPC_FPC策略下，母線電壓突變至760.9 V左右，電壓恢復時間約3.1 ms。電壓恢復至穩態后，存在一定的穩態誤差，約0.5 V。IMPC_FPC策略下，母線電壓突變至758.7 V左右。電壓恢復過程中，無振蕩與超調過程，電壓恢復時間約為3 ms。

不同控制策略下，HESS功率響應性能對比如表5所示。由對比結果可知，所提控制策略在面對大功率負荷突變時，電壓突變量最小，無振蕩過程，且調節時間短，具有最快的功率響應速度，同時避免了自適應調參算法的運算復雜性。

綜上，所提控制策略在面對大功率負荷突變時展現出更優的控制性能，驗證了所提控制策略的合理性及實用性。

5 結 論

針對微電網中混合儲能系統抑制母線電壓波動過程中功率響應慢、功率分配不合理等問題，提出混合儲能系統快速功率響應模型預測控制。通過仿真和硬件在環半實物仿真對所提控制策略進行驗證，得到如下結論：

1）提出的基于功率預測的HESS控制策略，通過儲能系統電流預測值與功率補償量獲得儲能系統參考功率，加快儲能系統功率響應速度，抑制直流母線電壓波動。

2）設計有理函數擬合的功率配置方案對參考功率進行優化配置，得到鋰電儲能與飛輪儲能的最優參考功率，實現飛輪儲能系統容量的最大化利用，減少突變功率對電池影響，延長電池使用壽命。

3）設計IMPC策略對鋰電-飛輪儲能系統進行控制，使實際電流快速跟隨參考電流，提高儲能系統的動態性能。

參 考 文 獻：

［1］ MENG Zihe， DUAN Jiandong， SUN Li. Voltage drop compensation technology for high-voltage and high-power DC energy storage power supply system［J］. IEEE Transactions on Industrial Electronics， 2023， 71（1）： 549.

［2］ 趙玲霞，王興貴，丁穎杰，等.基于三端柔性直流的光熱儲能站與新能源場站功率協同控制策略［J］.電機與控制學報， 2024， 28（6）： 131.

ZHAO Lingxia， WANG Xinggui， DING Yingjie， et al. Power coordinated control strategy of concentrating solar power with thermal storage and new energy stations integrated by three-terminal VSC-HVDC［J］. Electric Machines and Control， 2024， 28（6）： 131.

［3］ 許振宇， 石夢璇， 周建宇， 等. 基于飛輪儲能的網/儲協調虛擬同步機控制策略的小信號模型分析［J］.中國電機工程學報， 2020， 40（20）： 6236.

XU Zhenyu， SHI Mengxuan， ZHOU Jianyu， et al.Small signal model analysis of network/storage coordination virtual synchronous generator control based on flywheel energy storage system［J］. Proceedings of the CSEE， 2020， 40（20）： 6236.

［4］ 李進， 張鋼， 劉志剛， 等. 城軌交通用飛輪儲能陣列控制策略［J］. 電工技術學報， 2021， 36（23）： 4885.

LI Jin， ZHANG Gang， LIU Zhigang， et al. Control strategy of flywheel energy storage array for urban rail transit［J］. Transactions of China Electrotechnical Society， 2021， 36（23）： 4885.

［5］ 林莉， 林雨露， 譚惠丹， 等. 計及SOC自恢復的混合儲能平抑風電功率波動控制［J］. 電工技術學報， 2024， 39（3）： 658.

LIN Li， LIN Yulu， TAN Huidan， et al.Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations［J］. Transactions of China Electrotechnical Society， 2024， 39（3）： 658.

［6］ ZHANG X， GAMAGE D， UKIL A. Rising and falling edge compensation based faster control strategy for hybrid energy storage system in PV microgrid［J］. Electric Power Systems Research， 2021， 190： 106856.

［7］ SINGH P， LATHER J S. Dynamic current sharing， voltage and SOC regulation for HESS based DC microgrid using CPISMC technique［J］. Journal of Energy Storage， 2020， 30： 101509.

［8］ 陳亞愛， 林演康， 王賽， 等. 基于濾波分配法的混合儲能優化控制策略［J］. 電工技術學報， 2020， 35（19）： 4009.

CHEN Yaai， LIN Yankang， WANG Sai， et al. Optimal control strategy of hybrid energy storage based on filter allocation method［J］. Transactions of China Electrotechnical Society，2020，35（19）： 4009.

［9］ WANG B， MANANDHAR U， ZHANG X， et al. Deadbeat control for hybrid energy storage systems in DC microgrids［J］. IEEE Transactions on Sustainable Energy， 2018， 10（4）： 1867.

［10］ DUAN J， YI Z， SHI D， et al. Reinforcement-learning-based optimal control of hybrid energy storage systems in hybrid AC-DC microgrids［J］. IEEE Transactions on Industrial Informatics， 2019， 15（9）： 5355.

［11］ SHAN Y， HU J， CHAN K W， et al. Model predictive control of bidirectional DC-DC converters and AC/DC interlinking converters—A new control method for PV-wind-battery microgrids［J］. IEEE Transactions on Sustainable Energy， 2018， 10（4）： 1823.

［12］ GOLCHOUBIAN P， AZAD N L. Real-time nonlinear model predictive control of a battery-supercapacitor hybrid energy storage system in electric vehicles［J］. IEEE Transactions on Vehicular Technology， 2017， 66（11）： 9678.

［13］ RAHMAN A U， ZEHRA S S， AHMAD I， et al. Fuzzy supertwisting sliding mode-based energy management and control of hybrid energy storage system in electric vehicle considering fuel economy［J］. Journal of Energy Storage， 2021， 37： 102468.

［14］ PATEL S， GHOSH A， RAY P K， et al. Effective power management strategy and control of a hybrid microgrid with hybrid energy storage systems［J］. IEEE Transactions on Industry Applications， 2023， 59（6）： 7341.

［15］ ABIANEH A J， FERDOWSI F. Sliding mode control enabled hybrid energy storage system for islanded dc microgrids with pulsing loads［J］. Sustainable Cities and Society， 2021， 73： 103117.

［16］ MANANDHAR U， UKIL A， GOOI H B， et al. Energy management and control for grid connected hybrid energy storage system under different operating modes［J］. IEEE Transactions on Smart Grid， 2017， 10（2）： 1626.

［17］ CHONG L W， WONG Y W， RAJKUMAR R K， et al. An adaptive learning control strategy for standalone PV system with battery-supercapacitor hybrid energy storage system［J］. Journal of Power Sources， 2018， 394： 35.

［18］ WANG X， YU D， LE B S， et al. A novel controller of a battery-supercapacitor hybrid energy storage system for domestic applications［J］. Energy and Buildings， 2017， 141： 167.

［19］ SINGH P， LATHER J S. Power management and control of a grid-independent DC microgrid with hybrid energy storage system［J］. Sustainable Energy Technologies and Assessments， 2021， 43： 100924.

［20］ 趙靖英， 喬珩埔， 姚帥亮， 等. 考慮儲能 SOC 自恢復的風電波動平抑混合儲能容量配置策略［J］. 電工技術學報， 2024， 39（16）： 5206.

ZHAO Jinying， QIAO Hengpu， YAO Shuailiang， et al. Hybrid energy storage system capacity configuration strategy for stabilizing wind power fluctuation considering SOC self-recovery［J］. Transactions of China Electrotechnical Society， 2024， 39（16）： 5206.

［21］ SHEN Y， XIE J， HE T， et al. CEEMD-fuzzy control energy management of hybrid energy storage systems in electric vehicles［J］. IEEE Transactions on Energy Conversion， 2024， 39（1）： 555.

［22］ WANG X， ZHOU J， QIN B， et al. Coordinated control of wind turbine and hybrid energy storage system based on multi-agent deep reinforcement learning for wind power smoothing［J］. Journal of Energy Storage， 2023， 57： 106297.

［23］ 王力， 胡佳成， 曾祥君， 等. 基于混合儲能的交直流混聯微電網功率分級協調控制策略［J］. 電工技術學報， 2024， 39（8）： 2311.

WANG Li， HU Jiacheng， ZENG Xiangjun， et al. Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage［J］. Transactions of China Electrotechnical Society， 2024， 39（8）： 2311.

［24］ 周荔丹，張明珠，姚鋼，等.全直流型船舶微電網多時間尺度綜合能量管理［J］.電機與控制學報，2023，27（9）：180.

ZHOU Lidan， ZHANG Mingzhu， YAO Gang， et al. Multi time scale integrated energy management of full DC marine microgrid［J］. Electric Machines and Control， 2023， 27（9）： 180.

［25］ 李忠瑞， 聶子玲， 艾勝， 等.一種基于非線性擾動觀測器的飛輪儲能系統優化充電控制策略［J］. 電工技術學報， 2023， 38（6）： 1506.

LI Zhongrui， NIE Ziling， AI Sheng， et al. An optimized charging control strategy for flywheel energy storage system based on nonlinear disturbance observer［J］. Transactions of China Electrotechnical Society，2023，38（6）：1506.

［26］ GHANAATIAN M， LOTFIFARD S. Control of flywheel energy storage systems in the presence of uncertainties［J］. IEEE Transactions on Sustainable Energy， 2018， 10（1）： 36.

（編輯：邱赫男）