數學文化視域下高中數學概念教學研究

摘要：隨著新課改的不斷推進，數學文化受到了廣泛關注.在高中數學概念教學過程中，為了幫助學生提高學習技能，教師應對概念教學予以重視，并將其融入教學活動中，致力于發展高中生數學學科綜合能力.本文圍繞數學文化背景，在高中數學教學活動中融入概念教學，致力于深度剖析教學環節中運用數學概念的有效性作用，為優化教學路徑提供可行性方案.

關鍵詞：數學文化；概念教學；提升策略

概念教學是一線教師在教學實踐中主要應用的方法，對于優化高中數學教學工作起到至關重要的作用.教師基于數學文化背景，通過優化概念教學活動，為學生提供廣闊的學習路徑.然而，在高中數學教學過程中，要想體現數學概念教學的重要性絕非易事，它需要師生共同努力營造濃厚的學習氛圍，并將概念教學進行合理化應用，由此提高高中生數學核心素養.在教育教學工作中通過數學概念教學課題研究，提升教學質量、強化學生數學技能，促使高中數學教學取得良好育人成果.

1《指數函數的概念》生成環節教學片段

以北師大版《普通高中教科書數學必修第一冊》中《指數函數的概念》教學為例.為了清晰的解釋說明指數函數概念的生成過程，在教學過程中，教師通過引入數學概念環節，對數學知識進行解讀，由此增強學生實踐學習能力.

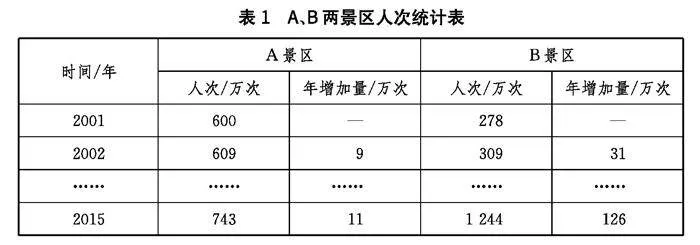
探究1隨著生活水平的提升，人們的休閑娛樂方式也更加多樣化，越來越多的人選擇旅游作為休閑娛樂方式，這使得近年來旅游數據逐年遞增，同時旅游數據也成了各景區制定門票價格的重要參考和依據.在此背景下，A景區為了增加收入，提升經濟效益，自2001年開始上漲景區門票價格，B景區為了保障游客數量，則直接取消了景區門票.表1為A、B兩景區的旅游人次統計表.

問題1結合表1分析A景區以及B景區旅游人次的變化，并結合分析結果探究兩景區旅游人次變化體現了怎樣的數學規律？

追問1怎樣通過數據處理的方式來直觀分析兩景區的旅游人數增長趨勢？

為了有利于觀察規律，根據表1，分別畫出A、B兩景區采取不同措施后的15年游客人次的圖象（如圖1、圖2）.

【設計意圖】聯系生活實際創設情境，結合旅游景區人次變化引導學生分析數據并繪制折線統計圖.由此直觀地展示兩個景區的人次變化規律，直觀形象地進行數學模型思維培養，為后續深入研究指數函數圖象做好鋪墊.［1］

問題2如果站在A景區負責人的角度，應該如何分析A景區旅游人次變化情況，怎樣才能科學預測A景區某一年的旅游人次？

問題3如果站在B景區負責人的角度，應該如何分析B景區旅游人次變化情況，怎樣才能科學預測B景區某一年的旅游人次？

追問2以B景區為例，思考如何通過計算對B景區旅游人次增長規律進行定量分析？

從2002年起，將B景區當年旅游人次除以上一年旅游人次的方式便可以得到以下結果.

2002年人次2001年人次＝309278≈1.11.

2003年人次2002年人次＝344309≈1.11.

……

2015年人次2014年人次＝12441118≈1.11.

【設計意圖】借助問題引導學生深入思考，鼓勵學生結合數據進行分析，由此提高數學分析能力.

追問3你可否運用規范的數學語言對B景區的變化情況進行描述，并用函數解析式的方式對B景區的人次變化情況進行表達？

解析：設x年后游客人次為2001年的y倍，那么得到y＝1.11x（x∈［0，＋∞））.

追問4y＝1.11x（x∈［0，＋∞））是一個函數嗎？

【設計意圖】以B景區為例，引導學生分析和探索旅游人次增長規律，在此基礎上再引導學生借助規律進行推理，用指數函數形式概括數學問題，由此借助解析函數的方式探索其對應關系，進而引出指數函數概念，同時通過引導學生自主探究來鍛煉和發展學生對指數函數概念的總結能力.［2］

探究2生物死亡后其體內的碳14會按確定的比率衰減，通常情況下，大約每經過5730年會衰減至原來的50%.人們將衰減至原來一半的這段時期稱之為“半衰期”.設剛死亡的動物體內碳14含量為1個單位，年衰減率為p.

問題1設生物體內碳14含量為y，結合所學知識，并根據指數函數概念，表示出1年后、2年后、3年后、5730年后以及x年后的碳14含量？

解析：一年后：y＝1－p.

二年后：y＝（1－p）2.

三年后：y＝（1－p）3.

……

5730年后：y＝（1－p）5730.

x年后：y＝（1－p）x.

【設計意圖】通過探究1學習指數增長模型；通過探究2探索指數衰減模型.通過對這2個探究題的系統性學習，幫助學生深入分析數學概念知識，由此提高學生數學學習能力.［3］依托數學化過程，幫助學生歸納和整理指數函數模型，以此引導學生進行問題分析與運算，強化學生數學綜合能力.

問題2試求年衰減率p，并表示出碳14含量y與死亡年數x之間的函數關系.

解析：已知條件（1－p）5730＝12，得p＝1－1215730，所以y＝12x5730（x∈［0，＋∞））.

追問y＝12x5730（x∈［0，＋∞））是一個函數嗎？為什么？

問題3通過探究和觀察的過程，對下面兩個函數解析式特征進行分析.

（1）y＝1.11x；（2）y＝12x5730（x∈［0，＋∞））.

問題4若用字母a代替底數，則兩個函數關系式怎樣表示？

問題5通過觀察得出，底數分別為1.11和12，即a＞0，那么a是負數或0可以嗎？

問題6在探究分析過程中，這一函數不屬于我們已學過的函數.如何為這類函數下定義？

【設計意圖】教學中利用函數模型激發學生的探究興趣，引導學生通過探究了解指數函數概念，增強學生對函數概念分析能力和規律總結能力.

2《函數概念》深化環節教學片段

以北師大版《普通高中教科書數學必修第一冊》中《函數概念》教學為例.在函數概念引入和生成的教學環節，學生能夠結合數學對應關系，建構函數概念思維，從而在函數概念表達形式中探索主要問題，以此進行辯證思維培養活動.問題探究活動能夠幫助學生清晰、直觀地理順函數概念知識，提高對函數教學活動的認同感和參與度.

問題尋找函數概念中的關鍵詞，簡明概括.

追問1同學們找到了函數概念中的關鍵詞，接下來請同學們分析總結以下函數概念的構成要素有哪些？

通過追問引導學生進一步深入探究，加深理解.

探究活動：將小球從左側盒子移到右側盒子（如圖3）.

追問2將圖3兩個盒子看成兩個非空集合A、B，f：A→B是函數嗎？若是，值域怎樣表示？

學生活動：教師組織學生進行分組學習活動，將前后桌四人分為一個小組.通過組內討論和組間交流學習，總結出函數構成的三要素，并與全班學生進行分享.與此同時，教師在教學過程中借助集合圖示的方式將抽象的知識轉化為更加直觀和具體的圖形，幫助學生降低學習的難度，加深其對所學概念的理解.

學生可能得到的結論：如果將小球的號碼與格子的號碼相對應，即1號球放入1號格子……此時，值域為｛1，2，3，4｝.

師生總結為在f：A→B函數關系中，可以以一對多，不可以以多對一.

【設計意圖】在函數概念學習過程中，教師通過對概念知識的總結與歸納，提高學生辯證思維能力，促使學生在探究實踐中發展數學技能，由此提高本節課知識學習效果.與此同時，教師通過設置實踐環節，幫助學生推導理論知識，增強學生動腦思考與動手學習的技能，為學生強化數學概念學習能力做好鋪墊.另外，在優化教學實踐中，教師通過發散性思維能力和批判性思維能力的拓展，提高學生數學思維品質，為學生全面發展搭建有利平臺.

3《條件概率》深化環節教學片段

以北師大版《普通高中教科書數學選擇性必修第一冊》中《條件概率的概念》教學片段為例.結合實例開展教學能拉近數學概念與現實生活之間的距離，增強二者之間的聯系，教師通過引導學生分析條件、概率與事件相互獨立性關系，使學生掌握解決問題的方法與技巧.

問題設A、B為兩個隨機事件，一般地，P（B|A）與P（B）不一定相等.如果P（B|A）與P（B）相等，那么事件A和B應滿足什么條件？

事件A與B相互獨立.

追問1如何證明呢？

請同學們通過合作探究的方式來證明自己的猜想.

當A與B相互獨立時，有P（AB）＝P（A）·P（B）成立，

有P（B｜A）＝P（AB）P（A）＝P（A）P（B）P（A）＝P（B）.

追問2如果已知P（A）與P（B|A），如何計算P（AB）？

∵P（B｜A）＝P（AB）P（A），∴P（AB）＝P（A）·P（B｜A）.

【設計意圖】引導學生探究與思考，并在此過程中讓學生學習和掌握數學概率知識，同時鍛煉學生的探究能力，使其能夠從直觀的視角出發，剖析事件之間的關系，由此進行數學邏輯思維培養活動.與此同時，在這一環節教學過程中，教師應幫助學生圍繞具體問題進行數學分析，從而開展主動思考與實踐活動，為學生綜合發展數學能力，提供可行性學習方案.

4《雙曲線及其標準方程》概念應用環節片段

以北師大版《普通高中教科書數學選擇性必修第一冊》中《雙曲線及其標準方程》教學片段為例.

例1已知雙曲線兩個焦點坐標為F1（－5，0），F2（5，0），雙曲線上一點P到F1、F2的距離之差的絕對值等于6，求雙曲線的標準方程.

變式 平面內，點P（x，y）滿足下列條件，求點P的軌跡.

（1）｜PF1｜－｜PF2｜＝6.

（2）｜PF1｜－｜PF2｜＝10.

（3）｜PF1｜－｜PF2｜＝0.

【設計意圖】概念應用主要以問題變化而進行變化，能夠實現理性教學和感性教學的融合目標，促使學生

形成舉一反三的能力，助力學生對數學概念知識的解讀與應用技能.教師借助例題引導學生運用所學數學概念解決問題，幫助學生進一步加深對數學概念的理解，同時構建更加完善的知識體系，促進學生邏輯推理能力以及數學抽象能力等方面的發展.

例2甲、乙兩地距離為10000m，炸彈爆炸時甲聽到炮聲比乙聽到炮聲晚了30017s，聲音以340m/s的速度傳播.爆炸點應在什么曲線上？并求其軌跡方程.

思考1在兩地同時聽到爆炸聲的情況下，則炸彈爆點處于怎樣的軌跡狀態？

思考2現實中怎樣確定爆炸點的位置才能更好地保障安全？

【設計意圖】通過數學文化內涵引導學生建構數學抽象思維，以此激發學生的探索欲和求知欲，培養學生主動探究與實踐學習能力.例2體現了化歸以及轉化思想，讓學生將數學抽象問題轉化為數學具象問題，以此進行數學解題活動，從而掌握數學解題的方法和技巧.在生活化問題的導入下，教師增強學生對知識點的系統解讀能力，為學生全面發展數學思想開辟全新路徑.同時，教師引導學生結合案例進行探究，并從現實角度考慮和分析問題，促進了知識的遷移，同時也鍛煉了學生的思維能力.

5結語

數學文化作為整個教育體系的重要組成部分，在教學實踐中起到重要的育人作用.在高中數學理論和實踐教學活動中，教師根據學生學情制定有效性教學方案，并在此基礎上引入數學文化，以此開發學生的數學智力，為學生形成良好的學習習慣做好鋪墊.結合當前高中數學教學現狀及教學問題，本研究圍繞數學概念教學方法提出相應的教學策略.數學教師應在概念教學過程中引入數學文化，幫助學生深度解讀數學概念知識，拓寬學生獲取知識的路徑，增強學生實踐學習技能，為學生綜合性、全面性發展奠定堅實基礎.

參考文獻

［1］劉永琳.數學文化視域下的高中數學教學研究［J］.數理天地（高中版），2023（11）：53－55.

［2］孫波.數學文化視域下的高中數學教學研究［J］.高考，2022（16）：48－50.

［3］范海濤.數學文化視域下的高中數學教學［J］.數學大世界（下旬），2021（6）：39.

*基金項目：

甘肅省教育科學“十四五”規劃2023年度專項課題“高中數學‘函數的概念與性質、冪指對函數’單元教學設計與實施研究”（項目編號：GS［2023］GHBZX0047）.