高中數學拔尖創新人才培養課程體系建構與實施

摘 要 基于高中生數學核心素養的提升，以“教是為了不教”的育人理念為指導，構建“三階”（鞏固基礎型課程、發展能力型課程、挑戰榮譽型課程）“五維”（德育素養、文化素養、寫作素養、建模素養、知識水平）的“三階五維”高中數學拔尖創新人才培養課程體系，從培養對象、培養內容、培養方式三個方面展示“三階五維”課程體系的實施路徑，以期為當前中學及中學數學教師所面臨的新挑戰提供思路與對策。

關 鍵 詞 拔尖創新人才；“三階五維”課程體系；高中數學；數學核心素養；強基計劃

引用格式 吳佐慧.高中數學拔尖創新人才培養課程體系建構與實施[J].教學與管理，2024（31）：16-19.

《國家中長期教育改革和發展規劃綱要（2010-2020年）》指出，要“推進培養模式多樣化，滿足不同潛質學生的發展需要”，同時為了貫徹落實全國教育大會精神，服務國家重大戰略需求，要加強加大拔尖創新人才的選拔培養。教育部在2020年1月印發了《關于在部分高校開展基礎學科招生改革試點工作的意見》（以下簡稱《試點工作意見》），“突出基礎學科的支撐引領作用”，標志著基礎學科招生改革試點正式啟動，迄今已遴選39所“雙一流”高校作為試點，又稱“強基計劃”。強基計劃強調探索多元錄取機制，專門培養有志趣、有創新潛質的優秀青年成為我國人才儲備軍，以此推動綜合評價改革，實現基礎學科人才選拔和人才培養的有機結合[1]。

黨的二十大報告中指出：“我們要堅持教育優先發展、科技自立自強、人才引領驅動，加快建設教育強國、科技強國、人才強國，堅持為黨育人、為國育才，全面提高人才自主培養質量，著力造就拔尖創新人才，聚天下英才而用之。實施科教興國戰略，強化現代化建設人才支撐。”[2]高中階段是學生個性形成、自主發展的關鍵時期，其中數學學科對學生綜合思維能力的提升，尤其是促成學生拔尖創新更為重要。目前對數學拔尖創新人才的理解存在概念不清、內涵不明、標準單一的問題，社會更側重于學生的數學學業成績和數學學科競賽成績，對拔尖創新學生的發現與培養不足。需要明確的是“拔尖”并不一定“創新”，具有“創新”精神也可能在數學學習上不“拔尖”。

鑒于此，項目組成員以“教是為了不教”的育人理念為指導，于2010年開始持續開展了關于高中數學拔尖創新人才（資優生）培養的研究，經過在柳州高級中學多年的探索與實踐，構建了“三階五維”高中數學拔尖創新人才培養課程體系，探索了高中數學拔尖創新人才培養的新機制，為當前中學及中學數學教師所面臨的新挑戰提供了思路與對策。

一、“三階五維”高中數學拔尖創新人才培養課程體系理論基礎

在培養高中數學拔尖創新人才的過程中，學校構建了以教育心理學家約瑟夫·蘭祖利的“三環模式”理論為核心的“三階五維”人才培養課程體系。蘭祖利的“三環模式”拓寬了對天賦學生的傳統定義，打破了以往單純依賴學術成績或標準化測試評估學生的局限性。他認為，天賦不僅體現在高分上，更應該重視學生個體的差異性，尤其是那些具備獨特創造力、非凡思維模式、創新表達方式以及強烈動機的學生，他們往往在傳統教育評估體系中被忽視或低估[3]。蘭祖利的“三環模式”理論強調三大要素——天賦行為、創意、投入，并認為學生的數學天賦與潛能不僅來源于智力水平，還需要具備高度的創造性和對學術、興趣的深度投入。這一多維度的評估體系更好地識別了那些在傳統教學中被忽視的非傳統型優秀學生。通過包容與多元的視角，蘭祖利的“三環模式”為教育者提供了一種新方法，讓他們能夠發現學生的潛在天賦，并提供更有針對性的高中數學拔尖人才課程體系，從而為學生的發展提供更多機會和更大空間[4]。

在此基礎上，“三階五維”課程體系深入融合了多種教育理論。首先，皮亞杰的認知發展理論強調學生的認知能力是通過主動建構知識實現的[5]，這與學校倡導的“教是為了不教”的理念高度契合。通過啟發式教學，我們希望學生能主動參與知識的建構過程，而非被動接受知識，從而培養獨立的思考能力與解決問題的能力。其次，建構主義教育理論強調學生在真實情境中通過協作、探究和反思來學習，這也為我們的課程體系提供了理論支持。通過在數學課堂中引入多維度的學習任務和開放性的數學問題，學生得以在實踐中提升自己的創造力與邏輯思維能力。

結合上述教育理論，“三階五維”課程體系通過多層級的數學課程設置以及多維度的評估方式、個性化的數學教學模式和創新型的數學學習環境，為數學拔尖人才提供個性化發展空間。學生不僅在學術上獲得高成就，同時還能培養出獨特的創造性思維和數學專業素養。我們的目標是通過這一模式，打破傳統高中數學教學的局限，真正實現學生個體差異的尊重與人才的全面發展。通過對這些數學拔尖創新人才的培養，最終為數學學科的發展與創新注入新的活力。

這種理論體系的應用，不僅為當前的數學教育改革提供了新思路，也為推動數學拔尖人才的成長提供了堅實的理論基礎和實踐路徑。在該體系的支持下，更多具備潛數學力但在傳統模式下可能被忽略的學生，得到了更廣泛的關注和培養，從而使他們能夠充分發揮自己的天賦與才能，成為未來學術領域和社會中的佼佼者。

二、“三階五維”高中數學拔尖創新人才培養課程體系建構

“三階五維”高中數學拔尖創新人才培養課程是基于國家課程和柳州高級中學數學校本課程，對原有培養課程進行再次整合、補充和完善，構建充分滿足學生個性化發展需求的數學課程體系，具有多樣性、挑戰性與跨學科性等三種特性，踐行“教是為了不教”的教育理念，最終實現人的終身可持續的發展以及實現自我價值。

1.三階

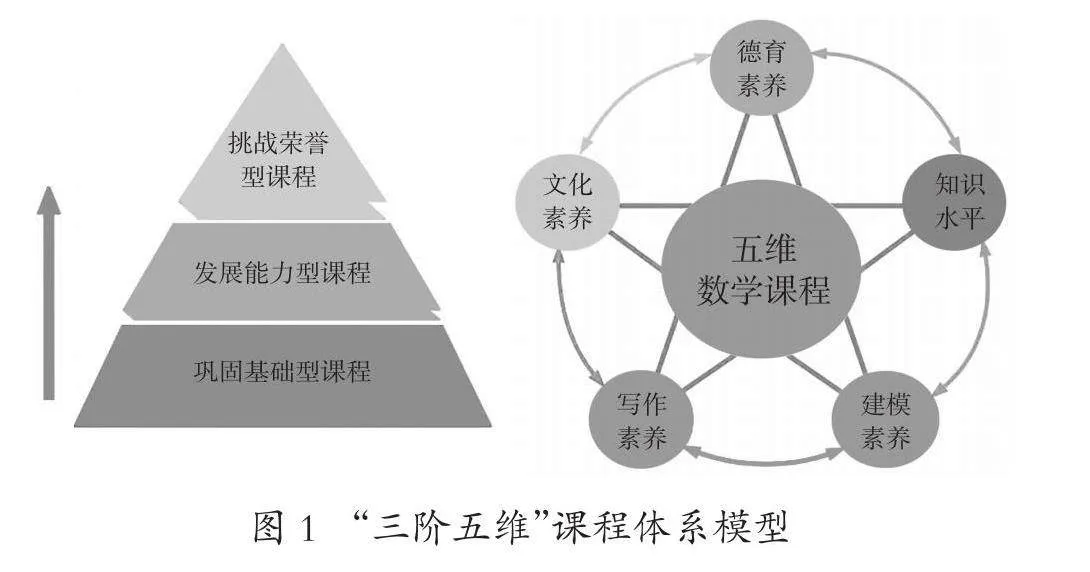
“三階五維”高中數學拔尖創新人才培養課程體系中的“三階”指鞏固基礎型課程、發展能力型課程和挑戰榮譽型課程。首先，鞏固基礎型課程的主要目的是拓寬學生數學基礎知識面，激發學生的數學學習志趣；教學內容涵蓋國家必修課程和柳州高級中學數學校本課程，注重數學基礎知識傳授，滲透數學高階思維，采用兩個行政班合班管理模式，基本統一教學內容、進度和測評。比如數學競賽的基礎專題講座、數學大學先修課講座、高觀點下的高中數學講座、數學文化、數學寫作、高校網絡公開課、數學建模初步以及科技創新中的數學等。其次，發展能力型課程根據蘭祖利“三環模式”引導學生對自己進行多維度的分析與測評，進行分專題的小班化教學以及導師制，選擇適合自己的選擇性必修課程；向數學拔尖創新人才提供國家選修課程和校本選修課程，采用獨立班級的課堂教學，讓拔尖創新人才在選擇性學習的過程中，發現并初步堅定自己的數學志趣。最后，挑戰榮譽型課程，適應特長發展需要，提升數學高階思維能力，給拔尖創新人才提供個性化學習選擇的機會，提升自我特長發展能力。比如：大學先修微積分、線性代數、強基數學、進階數學建模、數學競賽專題等[6-12]。

2.五維

“五維”是指拔尖創新人才培養數學課程涵蓋的維度，包括以下五個方面：其一，德育素養。在學生培養過程中我們要時刻把握“育人先立德”，要引導學生形成正確的人生觀、世界觀、價值觀，同時還要注意學生身心健康，且盡力提升學生的抗壓能力和克服困難的毅力、決心以及團隊合作能力以及學生的志向。其二，文化素養。對于數學拔尖創新人才培養我們不能只是對學生進行數學知識的講授，也要注意文化素養的培育。數學家丘成桐先生認為：文化修養不僅能夠培育人的意志，對科學研究也大有裨益。在學習數學的同時閱讀一些數學家的傳記，學習他們的精神，以及閱讀與數學文化相關的書籍，對數學的理解也是有一定作用的。其三，寫作素養。主要提升學生的文獻檢索、數學表達能力以及科研論文寫作能力。其四，建模素養。通過數學建模的教學提升學生的模型意識，實現學科融合，進而“會用數學眼光觀察世界，會用數學思維思考世界，會用數學語言表達世界”[13]。其五，知識水平。通過教師對學生“有限”知識的傳授及思維能力培養，促使學生養成自學的習慣，提升學生分析問題以及解決問題的能力，最終實現“教是為了不教”（如圖1）。

三、“三階五維”高中數學拔尖創新人才培養課程體系的實施

經過對柳州高級中學多年教學實踐的反思，筆者認為高中數學拔尖創新人才培養要從培養對象、培養內容以及培養方式三個方面著手。

1.培養對象：全體學生

最初學校對高中數學拔尖創新人才的認識具有一定的局限性，和大多數人一樣，簡單地認為數學競賽成績或高考成績優秀的學生就是所謂的拔尖創新人才，也就是大部分人認為的“智優生”。但通過對皮亞杰兒童心理學發展理論、建構主義教育理論以及約瑟夫·蘭祖利“三環模式”理論的學習以及研究，學校逐漸認識到高中數學拔尖創新人才培養對象應該是具有數學拔尖創新潛質的學生，是所有的學生。

創新是人的天性，任何學生都可能在某個方面具備創新的潛質。學生的能力素養是動態變化的，在學生成長的某些時期，不同的老師采用不同的培養方式教授不同的內容，也有可能會影響高中學生數學素養的提升，因此我們需要通過系統構建“三階五維”高中數學拔尖創新人才培養課程體系，采用優秀的師資隊伍對所有學生進行數學學習的啟智培根以及差異化的培養，為他們的個性化發展打下堅實的數學基礎。

2.培養內容：從高中數學學科知識到數學學科素養

第一，優化學校數學校本課程理念。根據不同層次的學生制定不同的數學課程目標，同時進一步優化校本數學課程結構，豐富完善校本數學課程，整合數學課程內容，加強校本數學課程的管理與實施，構建指向高中數學核心素養提升動態的“三階五維”課程體系，并通過項目式以及探究式等課程形式促進學生數學高階思維以及學習力的提升。

高中數學教學活動中知識的傳授并非僅僅局限于“教”與“學”的單向流程，而是基于深思熟慮的課程設置和獨具匠心的教學模式悄然實現知識的傳遞與深化。因此，需要數學教師不斷優化自己的教學內容，整合高中數學拔尖創新人才培養的教學資源，確保數學課程安排具有彈性。在汲取豐富的高中數學課程改革經驗的基礎上，教師致力于對課程設置方案進行更為精細的完善，強化高中數學各個學習階段中數學學科課程內容的有效鏈接，加深學校提供的數學課程與數學拔尖創新學生的互適性。

第二，通過相應的數學課程提升高中數學拔尖創新學生的數學知識積累能力以及數學素養五個維度的課程：德育素養、文化素養、寫作素養、建模素養、知識水平。例如初高中銜接課程、德育課程、數學文化、國家必修課程、國家選修課程、校本選修課程、數學競賽初步、強基課程、數學競賽拓展、數學寫作、大學先修課程以及數學建模課程等系列課程群，通過科學系統而深入的課程學習，讓學生的數學知識體系更加完善，基礎更加扎實，在強化學生數學基礎的前提下，增加數學課程的深度與寬度。

學生進入高中以后，在三年的數學學習過程中，我校充分尊重學生數學學習個體需求，根據學生自己的志趣，結合大數據精準靶向教學以及不同階段的心理測評，讓學生能夠更加清晰地認識自我，不斷激發自己數學學習的內驅力。

第三，培養學生的問題意識、批判性思維以及創新能力。丘成桐先生認為：一流人才，始自學“問”，最主要的是提出問題，我們要培養現在的年輕人，幫助他們提高找出重要問題的能力。我校通過高中數學拔尖創新人才培養“三階五維”課程的設置，引導學生獨立思考、提出問題，進而進行對比和批判性思考，打破常規數學思維的藩籬，發展學生的數學創新性思維。

第四，在真實情境問題的引領下，培養學生跨學科的綜合能力，促進學科間的深度融合。這一舉措不僅是對傳統數學單科教育的有力補充，更是為了進一步激發學生的創新思維，提升他們解決實際問題的能力。通過數學建模、科技創新以及STEM教育等多元化的教學手段，鼓勵學生將理論知識與實踐相結合，培養他們的綜合素質和創新能力。

3.培養方式：雙導師制下的小班化與動態調整的高中數學拔尖創新人才培養

（1）結合大數據精準靶向數學教學，確定各層次各類型課程的選修學生

基于學生個人情況，遵循自愿進出、雙向選擇的原則，實施小班化教學，并構建高中數學拔尖創新人才培養的動態調整機制。通過面試、“即學即考”的筆試、日常數學課堂的細致觀察，結合平時數學成績、強基數學實力、數學競賽表現、大學選修課程掌握情況、數學建模能力等多維度指標的綜合測評，將對不適應此類課程的學生進行妥善分流。同時，若其他類型班級中有學生展現出對此類課程的適應性，在其個人意愿的基礎上，我校將予以補充，以實現學生的差異化培養，并為每位學生量身定制個性化的培養方案。

（2）試行雙導師制度，即學術導師與項目導師協同合作模式

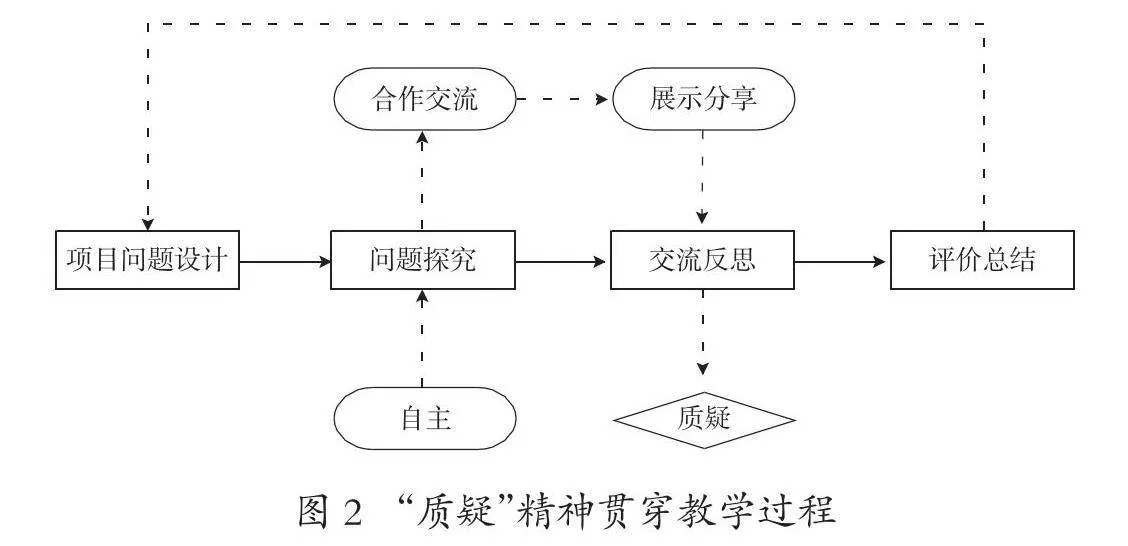
學術導師專注于高考、強基計劃、數學競賽以及大學先修課等學術領域的指導，而項目導師則主要負責數學建模、科技創新以及STEM教育等實踐項目的引導。此外，項目導師還將擔任學習小組或學習共同體的指導教師，以確保學生的實踐活動得以高效推進。無論是學術課程還是項目式課程，我校都秉持“自主、合作、分享、交流反思”的教學理念，并將“質疑”的精神貫穿于整個教學過程之中，以激發學生的求知欲和創新精神（如圖2）。

綜上所述，高中數學拔尖創新人才培養是一個系統工程，需要各方面的共同努力。同時“三階五維”高中數學拔尖創新人才培養課程體系的構建以及實踐也需要學校和教師的共同配合與努力。一方面，學校層面需要多維度的整合優勢高中數學教學資源，為其實施提供基礎的物質以及制度保障，比如有相應的資金以及完善相關的激勵政策等支持教師編寫數學拔尖創新人才培養校本教材講義等。另一方面，學校努力打造一支高素質數學拔尖創新人才培養的師資隊伍，增加能勝任“三階五維”高中數學拔尖創新人才培養的師資數量，強化師資培訓質量，有效調動數學教師的主動性以及自覺性，同時采取“引進來、走出去”的方式，為教師們提供共享優質資源，拓展他們的視野，努力更新他們的教育理念。希望通過“三階五維”高中數學拔尖創新人才培養課程體系的構建以及高中數學拔尖創新人才培養的新機制的探索，在師生的共同努力下，經過高中三年的培養與提升都能夠做到數學根基牢固，素養厚實，不同類型的師生都能得到相應的發展與提升。

參考文獻

[1]教育部等六部門關于實施基礎學科拔尖學生培養計劃2.0的意見：教高〔2018〕8號[A/OL].（2018-10-08）[2023-10-11].http：//w

ww.moe.gov.cn/srcsite/A08/s7056/201810/t20181017_351895.html.

[2] 習近平. 高舉中國特色社會主義偉大旗幟為全面建設社會主義現代化國家而團結奮斗： 在中國共產黨第二十次全國代表大會上的報告[EB/OL].（2022-11-01）[2023-10-11].http：//www.qstheory.cn/dukan/qs/2022-11/01/c_ 1129089160.htm.

[3][4] 蘭祖利，里斯. 豐富教學模式：一本關于優質教育的指導書[M].華華，譯.上海：華東師范大學出版社，2000：1，1.

[5] 沃茲沃思.皮亞杰認知和情感發展理論[M].5版.楊硯秋，譯.上海：華東師范大學出版社，2022：11.

[6] 吳佐慧.高中數學建模校本課程體系的構建與實踐[J]. 數學通訊，2022（02）：36-38+40.

[7] 吳佐慧，葉瀚文. 基于學術志趣的高中數學建模教學實踐研究[J]. 數學通訊，2021（02）：27-30+54.

[8] 吳佐慧，曾露儀.高中數學建模教學關鍵問題的探索與解決思路[J].廣西教育，2021（06）：60-63.

[9] 吳佐慧，曾露儀.拔尖創新人才培養視域下數學建模的教學設計與思考[J]. 數學通訊，2023（23）：14-17.

[10] 吳佐慧，彭培盛.中國大學先修課程（CAP）微積分的實踐研究——以柳州高級中學的教學實踐為例[J]. 數學教學，2019（11）：14-16+50.

[11] 吳佐慧.射影幾何在高中圓錐曲線問題中的應用[J]. 數學通訊，2020（14）：41-43+46.

[12] 吳佐慧，葉瀚文.HPM視角下的基本不等式教學[J]. 數學通報，2020（06）：37-42.

[13] 史寧中，王尚志.普通高中數學課程標準（2017年版）解讀[M]. 北京：高等教育出版社，2018：5.

【責任編輯 王澤華】