堅持學科育人，打造有活力的數學課堂

【摘 要】以“黃金分割”教學為例，呈現數學學科育人的三種模式：讓學生運用新知識，遷移新情境，體驗運用所學知識解決問題的過程；讓學生經歷感受美、發現美、探索美的過程，通過動手操作、探索等去發現和創造，體會畢達哥拉斯“萬物皆數”的意境；從三條線段成比例，特殊化為在同一直線上的三條線段成比例，發現黃金分割點，感悟“數學從內部產生”的道理。

【關鍵詞】初中數學；黃金分割；價值追求；大單元教學；教學設計

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2024）35-0060-04

【作者簡介】韓新正，江蘇省泰州市第二中學附屬初中（江蘇泰州，225300）黨總支書記、校長，正高級教師，泰州市特級校長。

教育不僅僅是傳授知識，?更重要的是促進人的全面發展和自我實現。華東師范大學葉瀾教授說，所謂教育，就是“教天地人事，育生命自覺”。教育的主陣地在課堂，因此，堅持學科育人，打造有活力的課堂，促進學生生命成長應成為課堂教學的追求。

一、數學學科育人的三個維度

在新課標實施的背景下，從學科教學到學科育人，從“育分”到“育人”的轉變，體現了教育價值認知的轉變。教育的本質是發展人、成就人，是致力于生命的成長。沒有人的成長，教育就沒有存在的價值，更談不上生命力。因此，在實際教學中，教師應該認真研讀課標，深刻理解教材編寫的意圖。不同的課堂教學體現了不同的價值追求，但一定都是指向人的發展和教學生成的課堂。

1.有活力的數學課堂是注重遷移應用的課堂

課堂不僅要傳授知識，更要激發學生學習的積極性和內驅力，而學生的積極性和內驅力不是天生的，它需要教師創設合適情境，巧妙設計問題，引導學生深入思考和實踐，在思考和實踐的過程中發現新知、“創造”新知，生成新知。新知在和舊知的融合下，形成知識結構，進而能運用所學解決新情境下的問題。這就是在培養學生“解決問題”的能力，是數學育人的本真追求。

2.有活力的數學課堂是“讓學生動起來”的課堂

學科思想和哲學思辨，是教學的靈魂。數學教學就是要“教給學生有靈魂的數學”。在學習知識的過程中，教師要更多教給學生能力、思維、品格等終身受用的素養。有活力的課堂就是要“讓學生動起來”，讓他們動嘴、動手和動腦。“動起來”一方面體現在引導學生調查研究，收集資料，動手實驗等。尤其是數學實驗，數學實驗不僅有助于學生理解和掌握數學基礎知識和基本技能，體會數學思想與方法，獲得數學基本活動經驗，也是主動建構和發展數學認知結構的過程。加強實驗教學，對于培養學生的核心素養具有重要的理論意義和實踐價值。另一方面，“動起來”體現在讓學生經歷知識形成的過程，并在此過程中，學會像“數學家一樣思考問題”。在“刷題”盛行的當下，有些教學異化為直接告知學生結論，省掉了學生經歷知識形成的過程，而這恰恰是學生培養能力、形成素養的關鍵過程。所以，教學要立足學生能力培養和素養提升，讓學生真正動起來。有活力的課堂必須促進全體學生發展，讓不同的學生有不同的發展。

3.有活力的數學課堂是引導學生演繹歸納的課堂

數學既有從實驗、操作中發現的定理、結論，如畢達哥拉斯定理；更多的還是“從數學內部產生”，歐式幾何的建立就是在五大公設的基礎上，通過邏輯分析、推理而形成完整的幾何體系，所以演繹和歸納是數學最重要的思想方法。有活力的課堂應該在現有的知識基礎上，通過弱化條件推出一般結論，或者通過強化條件，得出特殊結論，進而形成完整知識結構，這樣才有利于培養學生的邏輯思維和推理能力，這也是“數學是思維的體操”的應有之義。

二、有活力的數學課堂教學實踐

《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）在圖形的相似部分，對黃金分割的要993a05eeee4dfabee36a562ab7d4192e求是：通過建筑、藝術上的實例了解黃金分割。“黃金分割”這節課，人教版教材是安排在九年級上冊《一元二次方程》的“閱讀與思考”，是作為一元二次方程的應用來處理，定位于“了解”。蘇科版教材是放在九年級下冊《圖形的相似》的第2課時，本章第1課時是圖上距離和實際距離，第3課時介紹相似圖形，后面分別介紹相似三角形的性質和判定及其應用。下面筆者結合“黃金分割”這節課的教學，呈現基于三種不同價值追求的設計，談談如何打造有活力的數學課堂，實現學科育人。

1.綜合應用一元二次方程和比例的知識，經歷深度學習過程

師：我們已經學完了《一元二次方程》這一章，會解一元二次方程，并能運用方程思想解決實際問題，這是我們學習新知識的意義所在。今天我們就一起來探索一元二次方程的一些運用。現在我們再回到本章第一頁，先看看這個雕塑，有什么感想？

生：雕塑很有氣勢，形態很美……

師：生活中還有哪些形態很美的人、物、建筑？

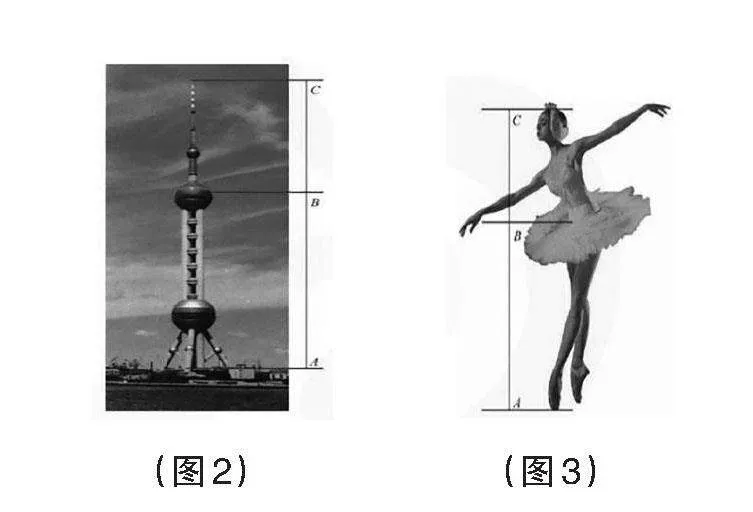
生：芭蕾舞演員、模特、東方明珠塔、我們學校的體育館……

師：這些形態優美、好看的人和建筑，用數學語言如何表述？

生：這些人和物可以抽象成線段，之所以形態優美，就是各線段的比例恰當、和諧。

師：在這一章的第一節課，我就布置大家收集這些形態優美的建筑和人物以及圖形，并研究這些線段的關系。請大家展示研究成果（以課本雕塑為例）。

生：我們通過測量雕塑上半身（腰以上）、下半身（腰以下）和全身高度，發現上半身∶下半身=下半身∶全身。

各組通過測量收集到的圖片，也發現了這一規律。通過查詢資料知道，如果把一條線段分成兩部分，其中較短線段與較長線段的比等于較長線段與原線段的比，中間的點就是黃金分割點，這個比值就是黃金分割數。

師：我們能求出這個黃金分割數嗎？

學生小組合作，共同完成下面的抽象建模過程。

如圖1，設AB = 1，BC = x，其中BC是較長線段，那么AC = 1 - x。根據條件得到（1 - x）∶x = x∶1，也即x2 + x - 1 = 0，解方程得x = [?1±52]，根據線段的實際意義，x = [?1+52] ≈ 0.618。

[A][C][B][x][1 - x]

（圖1）

師生一起探討黃金分割在生活中的運用。

【設計意圖】上述教學是將“黃金分割”作為一元二次方程的應用的課堂教學。設計者把本節課定位為，在系統學習了一元二次方程的基礎上，把黃金分割作為一元二次方程遷移運用的結果，體現的是學生深度學習的成果。設計者通過跨章節的專題研究，綜合運用所學知識，創新發現黃金分割（盡管黃金分割早已被發現，但對學生來說，確是研究成果）。

2.從欣賞美圖開始，體驗數學實驗魅力

一上課，教師就給學生展示如下兩組圖片。

師：圖2、圖3給我們的感覺首先是很美，為什么感覺美呢？那就要值得探討了。無論圖2還是圖3，都可以把鐵塔和人體抽象成線段，看來就是研究各線段之間的關系，課本上給我們做了提示，有線段AB，BC，AC。那我們怎樣研究它們的關系呢？

師：最常見的關系就是三條線段的和差倍分關系。在我們動手測量前是否先思考一下，有哪些關系可以先排除掉？

生：和、差、積可以排除。因為同樣的物體，如果圖片尺寸不同，那么它們的和、差、積不相同，如果把線段相除，這和圖片大小無關，因為是等比例縮放的。

師：很好！那大家先量出三條線段的長短，再分別計算[BCAB和ABAC]的比值，看看有什么發現？

教師課前準備好尺寸不等的上述圖片以及課本上的圖片，并給足學生測量時間，通過小組合作得出各組的數據，發現比值基本都在0.62附近，容易得出[BCAB=ABAC]。

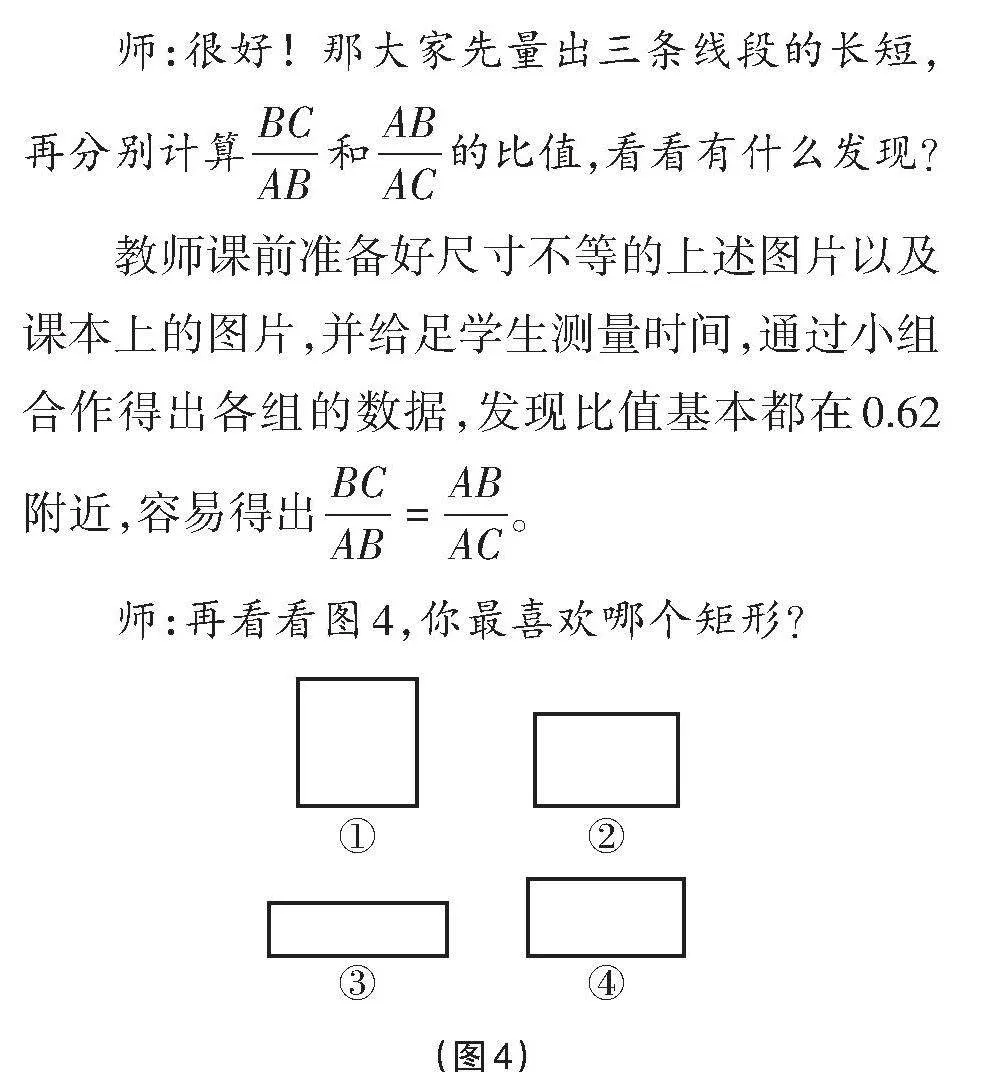
師：再看看圖4，你最喜歡哪個矩形？

全班調查后，多數學生喜歡②，感覺②看起來更美觀，那么就來看看美觀的奧秘，量出該矩形的寬和長，看看比值如何？全班動手測量計算后，發現寬和長的比值也在0.62附近。

師：如果一個建筑物這樣建設，應該是比較美觀漂亮的吧！剛才我們通過感受圖形美，并在測量和計算中發現了一些規律，那么怎樣從數學的角度來證明呢？也就是如果等式[BCAB=ABAC]成立，那么點B的位置在何處？

學生接下來進行代數推理，很容易得出黃金分割數。

【設計意圖】上述教學是體驗數學活動價值的課堂教學。教學從展示若干圖形開始，讓學生進行比較：為什么有些圖看起來很美，而有些圖不美，引導學生動手測量，探索并發現數據規律。設計者通過教學，讓學生感悟數學美，激發學生探究美的奧秘。這也是數學實驗的魅力所在，符合學生的認知規律。

3.強化外部條件，從數學的內部進行推理，感悟數學美

師：上一節課，我們學過了四條線段a，b，c，d成比例，可表示為[ab] = [cd]。如果b = c，那么[b2=ad]，我們把b叫作a，d的比例中項。

師：學習數學，有時需要弱化條件，推出一般性；有時需要強化條件，發現特殊性。今天，在上述基礎上，我們做進一步設想，把三條線段的關系進一步特殊化。如圖5，在線段AC（d）上取一點B，使得AB = a，BC = b，且滿足[ab] = [bd]呢？能否在線段d上找到B點？如果有，那么B點在線段d的什么位置？

師：若B點存在，如何求出b與d的關系？

生：直接解方程可得，其中把b看成未知數，d是已知數，可列出方程b2 = d（d - b）。

生眾：整理得b2 + db - d2 = 0。解得b =[?1±52d]，再根據題意，整理可得b = [5?12d]。

師：看來這一點是存在的，而且是一個特殊的點。再考慮一下，這條線段上像這樣的點有幾個？

生：兩個。根據線段的對稱性。

師：通過上面的探索，我們發現：原來成比例的四條線段[ab] = [cd]，當b = c時，三條線段成比例，即[ab] = [bd]，也就是[b2=ad]，出現了比例中項。再把這三條線段都同時落實到一條線段上時，又出現了特殊的點。這樣的做法給我們什么啟示呢？

生：不斷強化條件，讓條件不斷特殊化，能有很多科學發現。

隨著這一發現，大家把線段上的這一點叫作黃金分割點。

【設計意圖】上述教學是強化外部條件，從數學的內部進行推理的課堂教學。在學習了線段成比例，特別是三條線段成比例（比例中項）之后，進一步特殊化條件，大膽設想，如果一點把一條線段分成兩段，且短線段∶中線段=中線段∶原線段，這個點有什么特殊性？為什么會有此想法？源于畢達哥拉斯的“萬物皆數”。學生不僅能感悟數學推理和知識遷移的價值，更知道從數學內部產生新知識的方法。

通過有活力的課堂教學，學生不僅能習得知識和技能，更能收獲核心素養的發展。立足學生核心素養發展，集中體現數學課程育人價值，是新課標賦予教師的時代使命。只有基于價值追求的課堂教學才能培養出“會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界”的時代新人。