基于近場動力學的復雜界面雙材料結構研究

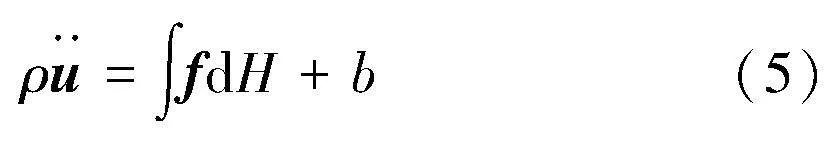
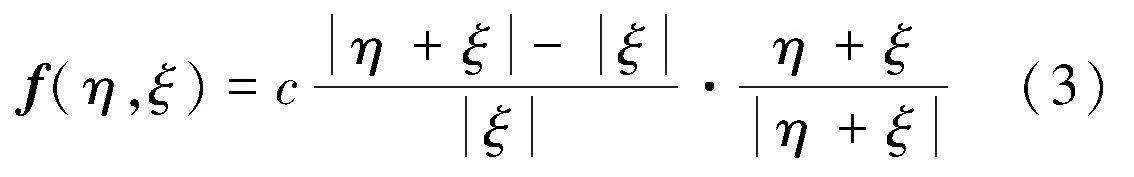
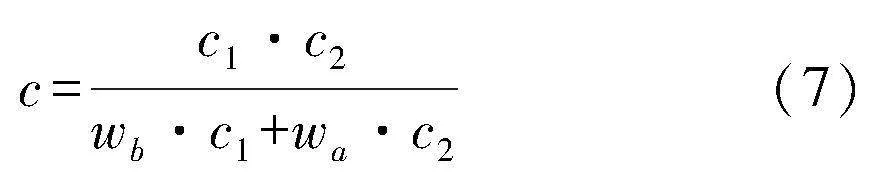
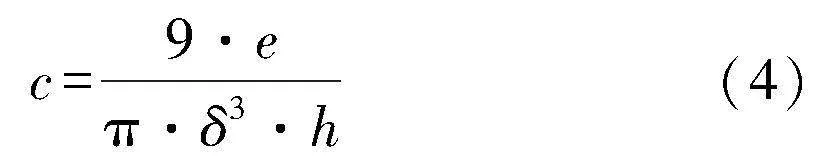
摘 要：為了將近場動力學方法應用于復雜界面的雙材料結構，以鋸齒形界面為例，基于PD“串聯”鍵理論開發復雜界面雙材料結構PD求解程序，通過單、雙材料平板進行拉伸仿真分析，利用FEM解驗證PD方法及程序的準確性。結果表明：PD方法在準靜態模擬中具有較高的準確性。PD程序所得位移結果：在y=0.005 m處，x位移相對誤差低于5%；在x=0 m處，y位移平均相對誤差低于6.08%。程序所得位移結果在小模量比、小載荷下更準確。

關鍵詞：近場動力學；有限元；雙材料；“串聯”鍵理論；界面形狀

中圖分類號：O341; TB331" 文獻標志碼：B" 文章編號：1671-5276（2024）05-0037-03

Study on Bimaterial Structure with Complex Interface Based on Peridynamic

Abstract：In order to apply the near field dynamics method to the bimaterial structure with complex interface， this paper， taking the serrated interface as an example， develops a PD solution program for the bimaterial structure with complex interface based on the PD 'series' bond theory， and verifies the accuracy of the PD method and program through the tensile simulation of single and bimaterial plates and by using the FEM solution. The results show that PD method has high accuracy in quasi-static simulation. The displacement results obtained by PD program indicate that the relative error of x displacement is less than 5% at y=0.005 m， the average relative error of y displacement is lower than 6.08% at x=0 m， and the displacement results obtained by the program are more accurate under small modulus ratio and small load.

Keywords：peridynamic；FEM；bimaterial；“series” bond theory；interface shape

0 引言

雙材料結構界面處的力學性能一直是相關研究的重點。目前主要的數值模擬方法有有限元法［1］、擴展有限元法［2］和邊界元法［3］等。其中，有限元法運算效率較低；擴展有限元法在多裂紋擴展和相互作用問題中適用性較差；而邊界元法在雙材料界面問題的應用相對較少［4］。

SILLING［5］在2000年提出近場動力學（peridynamics，PD）理論，該理論基于非局部作用思想，采用空間積分形式來描述物質內部作用，彌補了前述數值模擬方法的不足。秦洪遠等［6］利用改進的近場動力學鍵理論研究了復合材料單向板的變形與破壞問題。王芳、張恒等［7-8］針對雙材料界面問題提出了“串聯”和“并聯”鍵理論。

在實際生產中由于工程誤差等原因，材料交界面并非是完全光滑的平面，而目前針對雙材料結構的研究中，均將材料交界面設定為理想的平面。本文基于Matlab平臺，利用“串聯”鍵理論開發了復雜界面的雙材料結構PD求解程序，進行單、雙材料平板拉伸仿真模擬，利用FEM解驗證了PD方法及程序的準確性。

1 準靜態模擬中的PD鍵理論

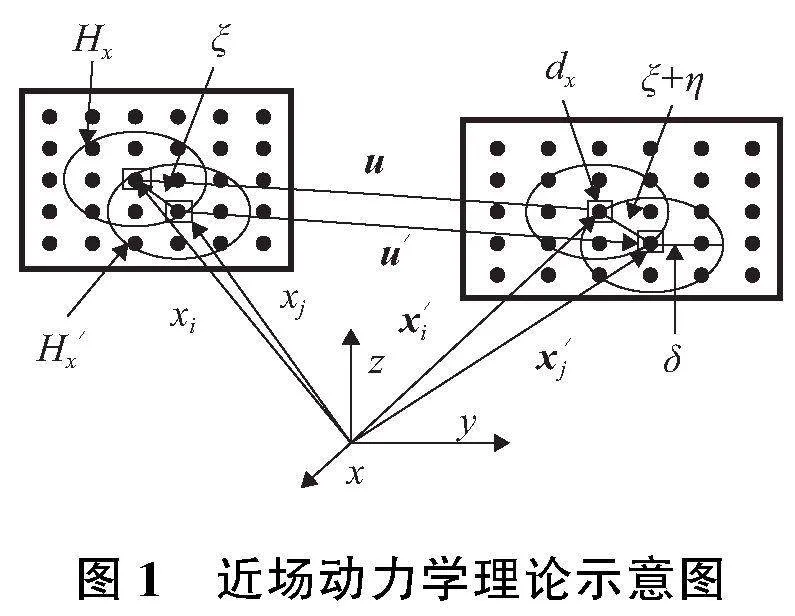
近場動力學模型假設每個物質點與一定范圍內的物質點通過鍵（bond）相連，如圖1所示。xi與xj為固體區域中任意兩個物質點；Hx與H′x分別為xi與xj的域，即近場鄰域。近場鄰域的大小由近場范圍δ決定；dx為物質點所在微元六面體（或矩形）的邊長；x′i與x′j分別為物質點xi與xj變形后的位置矢量；u與u′分別是變形后xi與xj的位移矢量；兩點間相互作用可以用參考鍵ξ與變形鍵ξ+η的函數表示，參考鍵及變形鍵表達式如下：

ξ=x′-x（1）

η+ξ=u′-u+ξ（2）

在線彈性問題中兩物質點間力密度矢量函數可以表示為

式中：力密度矢量函數f（η，ξ）是點對點的矢量函數，其定義為質點xj施加在質點xi上單位體積的力，兩質點間力密度矢量大小相等，方向始終與相對位矢平行；c為近場動力學常數。在鍵理論中，鍵常數計算式如下：

式中：e為材料的彈性模量；δ為設定的近場范圍；h為設定的模型厚度。

近場動力學中運動方程表達式為

式中：H為近場領域；b為外力。

啟用自適應動力松弛，通過引入虛擬慣性和阻尼項得到第n次迭代時：

2 復雜界面雙材料結構PD求解程序

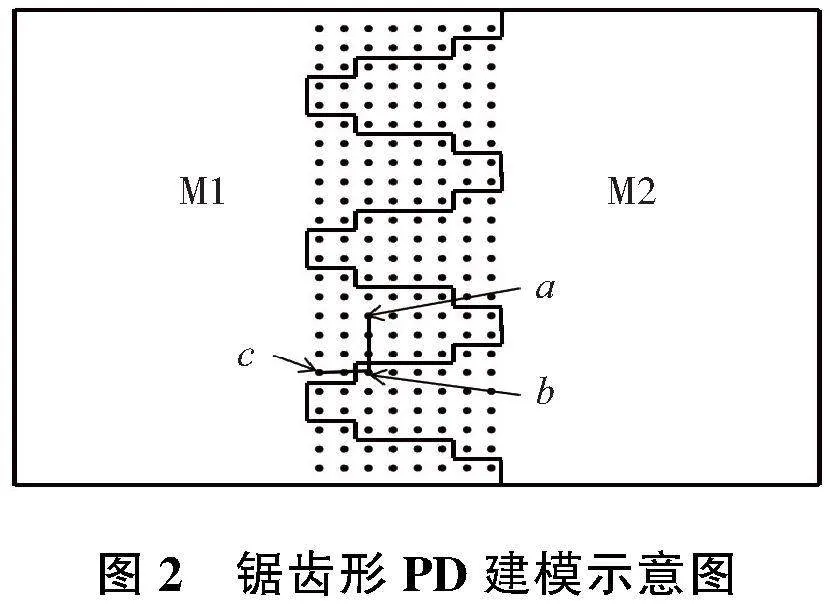
在材料M1、材料M2組成的雙材料結構中，存在3種PD鍵：M1-M1鍵、M1-M2鍵、M2-M2鍵，其中M1-M2鍵的PD常數c與兩種材料均屬性相關。在“串聯”鍵理論中，M1-M2鍵的近場動力學常數與距離加權函數有關，此時式（4）改寫為

式中：c1、c2分別為材料M1、M2的鍵常數；wa、wb為距離加權的權函數，分別表示一對M1-M2鍵中c1、c2的距離占比，它由物質點與材料交界面的距離決定。圖2為鋸齒形界面的PD離散示意圖，a-b鍵與c-b鍵同為以物質點b為中心的M1-M2鍵，但二者的距離加權函數不同，則PD系數c不同。因此，在Matlab平臺中，利用編程逐一確定每對M1-M2鍵的PD系數c，即可實現對界面位置的描述，進而實現復雜界面雙材料結構PD求解程序。

3 程序驗證

3.1 準靜態模擬中PD方法的準確性驗證

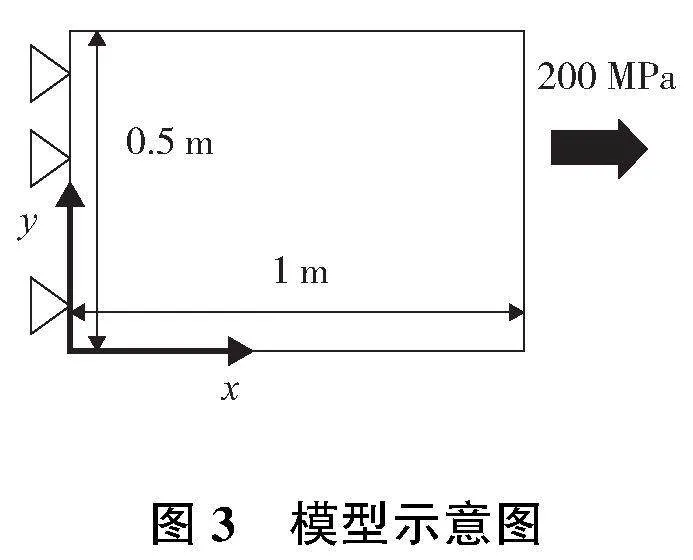
在利用平板拉伸仿真驗證程序準確性之前，需要先驗證PD方法在準靜態模擬中的準確性。圖3為模型示意圖，左端固定，右端施加均布壓強200 MPa。材料參數如下：彈性模量200 GPa；泊松比1/3。

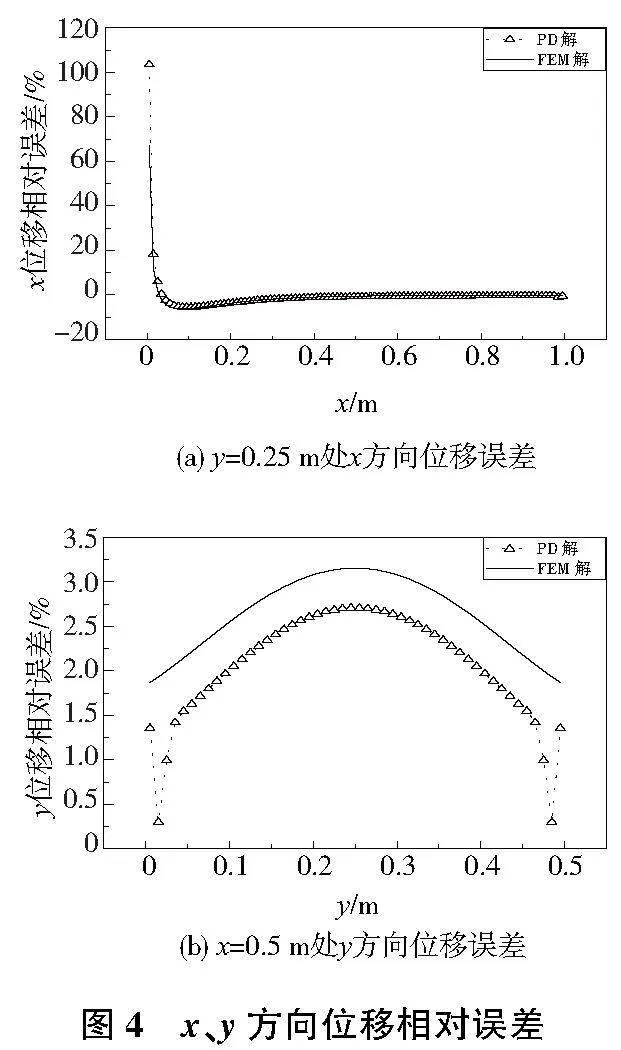
圖4為PD解、FEM解相對于解析解的x、y位移平均相對誤差。由圖4得：1）PD解存在表面效應，表面效應即PD理論在材料邊界處由于近場鄰域不完整而出現的誤差增大現象；2）除個別邊界點以外，兩種方法均具有很高的準確性；x方向上PD解與FEM解基本一致，誤差均在5%以內；y方向上，PD解誤差低于2.8%，大約為FEM解的0.76倍。綜上，在準靜態模擬中PD方法具有較高的準確性，可以利用平板拉伸仿真驗證PD程序的準確性。

3.2 復雜界面雙材料結構PD程序驗證

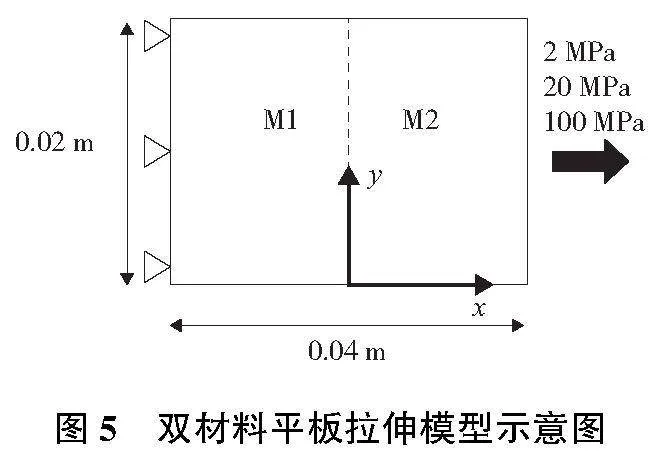
建立鋸齒形界面的二維雙材料結構PD求解程序，在3種載荷、3組模量比下進行二維平板拉伸仿真，并利用FEM解驗證PD程序的準確性。雙材料平板拉伸模型示意圖如圖5所示，模型左端固定，右端分別施加均布壓強2 MPa、20 MPa、100 MPa。左邊為材料M1，彈性模量固定為80 GPa，右邊為材料M2，在典型算例的模量比范圍內選取3組模量比，M1∶M2為：2倍、26倍、80倍，兩種材料泊松比均為1/3。

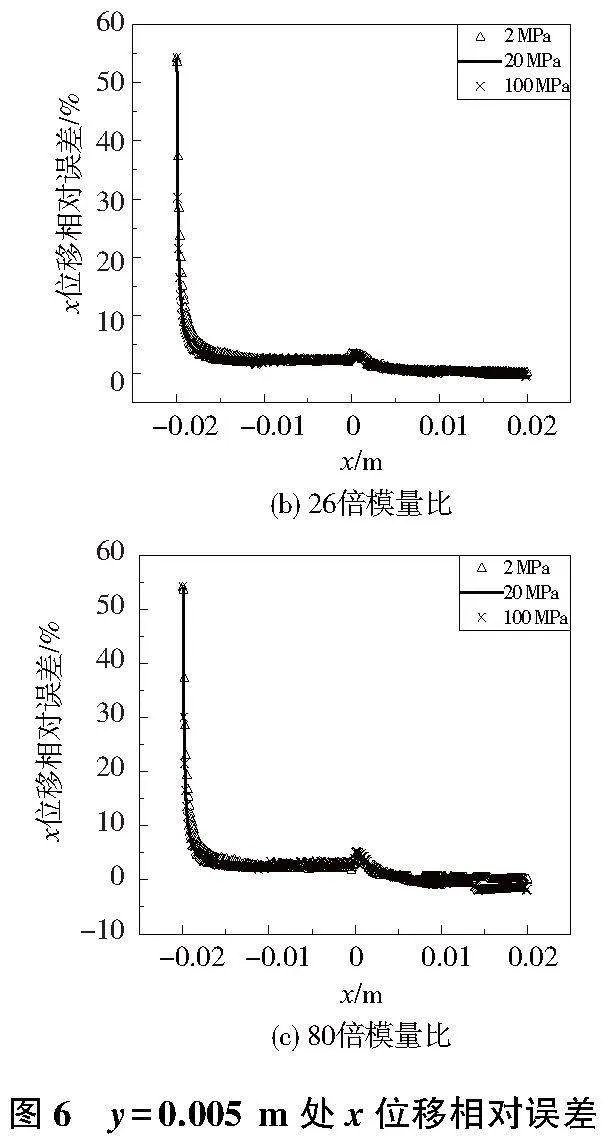
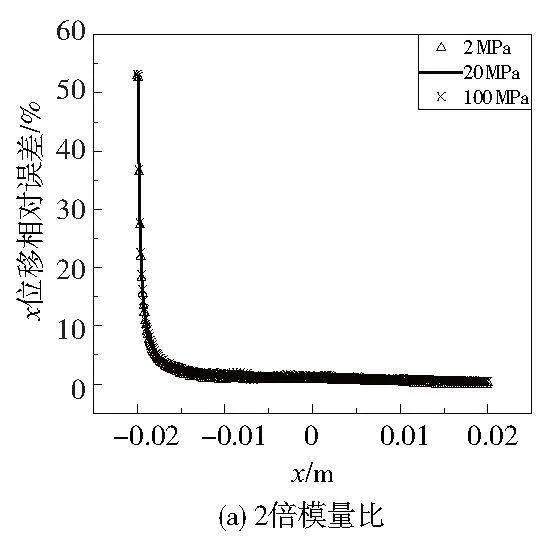
考慮到表面效應，針對平板內部xgt;-0.015m的部分進行分析。如圖6所示，3種載荷下誤差基本一致，均在5%以內；隨著模量比的增大，在x=0m（材料交界）處誤差出現一定波動，大載荷下波動更加明顯。

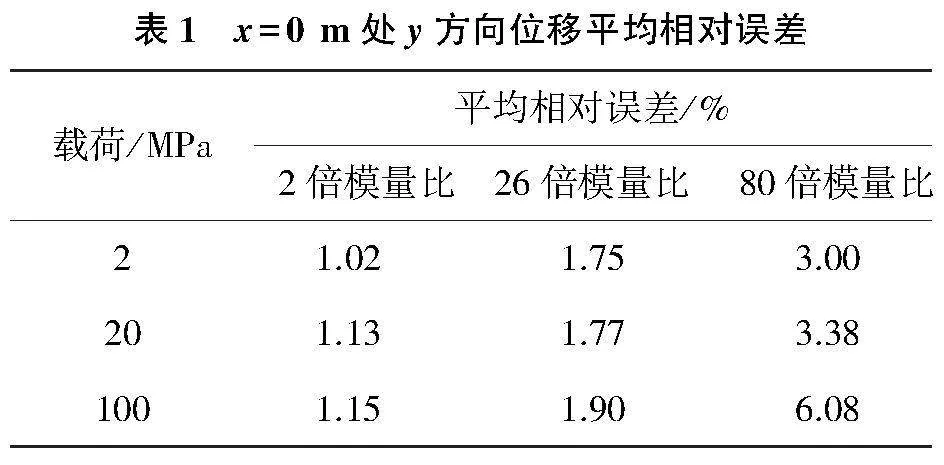
考察x=0m處y位移的平均相對誤差。考慮到表面效應，分析針對平板內部0.002 5mlt;ylt;0.017 5m處。如表1所示，y位移平均相對誤差在80倍模量比、100 MPa載荷下達到最大值6.08%。同時可得，相同模量比下，載荷越大誤差越大；相同載荷下，模量比越大誤差越大。

由上述分析可知，程序所得位移結果在材料交界處、大模量比、大載荷下誤差較大。下面逐一進行分析。

1）材料交界處：界面處“串聯”鍵理論微模量表達式（7）基于剛度等效原則，與真實情況存在一定誤差。在M1（或M2）材料內部，式（7）退化為近場動力學鍵理論微模量表達式（4），其誤差小于前者。因此，在界面處出現誤差增大現象。

2）大模量比、大載荷：模量比及載荷的增大導致位移增大。因此，程序的迭代時間越長，誤差累積越大。

4 結語

1）PD方法在準靜態模擬中存在表面效應；除個別邊界點外，x位移相對誤差低于5%，與FEM解基本一致；y位移相對誤差低于2.8%，約為FEM解的0.76倍。

2）在y=0.005m處，PD程序所得3種載荷下x位移相對誤差在材料交界處出現波動，大載荷下波動更加明顯；3種載荷下，x位移相對誤差基本一致，均低于5%。

3）在x=0m處，PD程序所得3種載荷下y位移平均相對誤差低于6.08%。

4）PD程序所得位移結果在小模量比、小載荷下更準確。

5）加密網格可以在一定程度上減小誤差。

參考文獻：

［1］ 鄭俊，周晚林，姜鑫. 復合材料層壓板損傷修復與評估［J］. 機械制造與自動化，2018，47（1）： 84-87.

［2］ 鄭安興. 擴展有限元法及其在巖體裂隙擴展模擬中的應用研究［D］. 上海：上海交通大學，2015.

［3］ 谷巖，張耀明. 雙材料界面裂紋復應力強度因子的正則化邊界元法［J］. 力學學報，2021，53（4）：1049-1058.

［4］ 劉邦劍，盛冬發. 壓電材料反平面斷裂問題的邊界元方法研究［J］. 科學技術創新，2022（4）：86-89.

［5］ SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces［J］. Journal of the Mechanics and Physics of Solids，2000，48（1）：175-209.

［6］ 秦洪遠，李玲，王偉，等. 基于改進型近場動力學方法的復合材料單向板變形與破壞分析［J］. 宇航材料工藝，2020，50（4）：19-23.

［7］ 王芳. 雙材料界面及其力學性能的近場動力學研究［D］. 武漢：武漢理工大學，2015.

［8］ 張恒，張雄，喬丕忠. 近場動力學在斷裂力學領域的研究進展［J］. 力學進展，2022，52（4）：852-873.