隧道掘進爆破粉塵運移規律研究

摘要 為了掌握隧道掘進爆破粉塵的運移規律，以某工程隧道掘進爆破為研究對象，采用數值模擬的方法，分析了隧道內氣流場的分布規律，揭示了粉塵濃度隨時間的變化規律，明確了不同粒徑粉塵的沿程沉降特征，并通過現場監測驗證了數值模擬的準確性。研究結果表明：爆破后2～6 s內，粉塵非常密集；爆破10～100 s內，粉塵在氣流作用下逐漸擴散；爆破產生的大顆粒會在重力作用下快速沉降而停止運動，而小顆粒會在風流作用下繼續在巷道流動。

關鍵詞 粉塵濃度；隧道爆破；運移規律；數值模擬

中圖分類號 U416.1 文獻標識碼 A 文章編號 2096-8949（2024）18-0051-04

0 引言

鉆爆法是隧道工程中應用最廣泛、性價比最高的開挖工程施工方法之一，但在爆破過程中會產生大量濃度極高的粉塵。高濃度粉塵不僅極大地影響了隧道施工的安全和進度，而且對作業人員的身體健康會造成嚴重威脅。如何快速有效地引入新鮮風流稀釋并排出隧道內的粉塵是隧道施工通風的重要環節。YU H等[1]利用數值模擬技術研究了爆破后硐室采場因通風而產生的粉塵質量濃度變化，并通過現場實測驗證了模擬的可靠性。林榮漢等[2]研究了高海拔礦山隧道掘進工作面粉塵運移規律并優化了通風除塵系統。王應權[3]結合實際工程分析了長大鐵路隧道施工通風方案的選擇及優化。曹正卯等[4]指出石隧道爆破中，炸藥發生強烈的化學反應的同時會產生沖擊波，隧道內的粉塵主要是沖擊波作用產生的。該文采用數值模擬方法，分析了隧道爆破后粉塵濃度隨時間的變化規律以及不同粒徑粉塵的沉降規律，并通過現場實測驗證了數值模擬結果的準確性。研究結果可為類似隧道爆破粉塵防控提供理論依據。

1 工程概況

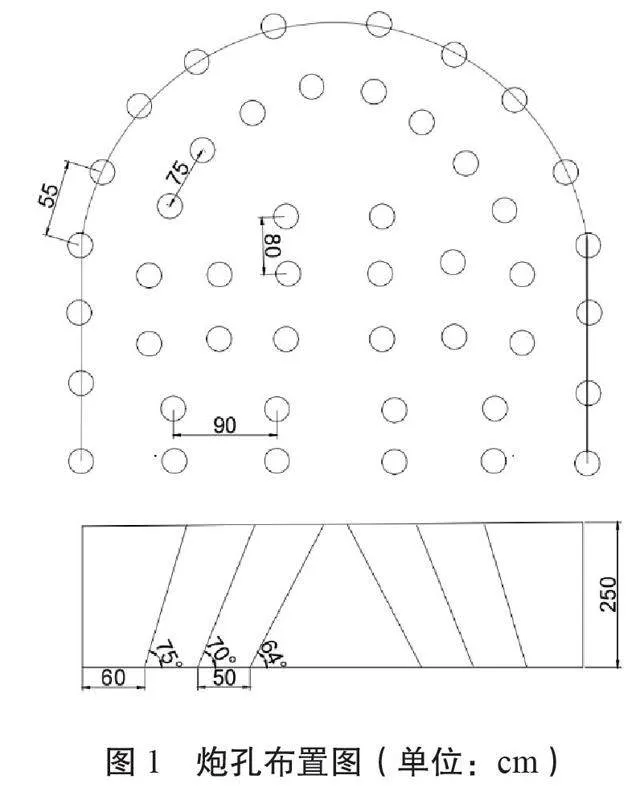
該文以某工程隧道掘進爆破為研究對象，該隧道圍巖為Ⅳ級，隧道入口處，已使用大型掘進機進尺30 m左右，由于巖石結構改變，巖石硬度變高，掘進機已無法使用，故決定采用爆破的方式開挖。隧道采用半圓拱斷面，斷面尺寸為凈寬5.2 m×高度4.2 m。設計爆破參數如圖1所示。

2 粉塵顆粒運動的控制方程

在計算隧道爆破粉塵運動軌跡的過程中，只考慮了重力和阻力的影響，其他力可以忽略不計。粉塵顆粒運動的平衡方程為：

為了獲得粒子的湍流擴散規律和粉塵濃度分布，在分段時間內對瞬時速度進行積分，即以離散的時間步長進行積分，從而得出粒子軌跡方程。

3 幾何模型的建立與求解

3.1 幾何建模與網格劃分

在對數值模擬結果影響不大的情況下，為了更方便物理建模，將粉塵輸送空間適當簡化如下：（1）將隧道簡化為一個截面半徑為4 m、長度為100 m的半圓拱空間；（2）考慮風管氣流對粉塵的影響，不考慮隧道內其他設備的影響；（3）其他工序產生的粉塵和底板的升降不考慮[5]。

基于以上的簡化和假設，利用solidworks軟件，以實際巷道爆破空間為基礎，按1∶1的比例建立三維幾何模型。其中，隧道風管懸掛在隧道右上方，直徑1 m，距底板距離3 m，風管出口至掌子面距離20 m。幾何模型結果如圖2所示。

3.2 仿真參數及邊界條件設置

通過廣泛查閱隧道爆破粉塵輸運特性、輸運徑分布的相關文獻，結合煤礦巷道領域的相關研究[6-7]，得到離散相模型參數、噴射源參數的邊界條件，根據Fluent軟件中離散相模型設置的要求。數值模擬參數如表1所示。

4 數值模擬結果與分析

4.1 隧道內氣流場分布分析

爆破粉塵顆粒的運動一般都發生在連續相的氣流場中。為了研究粉塵在巷道中的分布規律，設置風管的出口為速度入口，入口速度為20 m/s。隧道內氣流場分布圖3所示。

（1）氣流從風管噴出，沿著隧道右側朝向掌子面方向，與掌子面相撞后向隧道左側外流，在風道出口和掌子面之間形成了回流區域。在這個區域內，部分回流氣流受到沖擊和混合，與出口的氣流融合，導致原有的氣流場遭受強烈擾動，形成了高度湍流的渦流區域。

（2）大部分的氣流在與掌子面相碰后從漩渦區回流，但隨后繼續向前流動。在距離掌子面30 m處，氣流速度逐漸減小，氣流場分布逐漸趨于穩定和均勻。風流速度基本穩定在每秒0.5 m左右。

（3）風流初速度為20 m/s。在與周圍邊界層進行動量交換后，風速逐漸減小。在整個隧道流場中，風速在漩渦區具有最大風速，其次是過渡區，而在穩定區的風速則較小且均勻。

4.2 粉塵濃度隨時間的變化規律

將掌子面設置為粉塵面，并給予粉塵4 s的釋放時間。切割高度為Y=1.5 m（呼吸帶高度）的水平面作為濃度峰值監測面，觀察該平面上5 s、10 s、30 s、60 s、100 s處粉塵濃度峰的分布格局，如圖4所示。

（1）隧道爆破時產生的大量粉塵從掌子面高速噴入巷道。此時粉塵濃度高達400 mg/m3。在2～6 s內，爆破粉塵的濃度密集，大部分聚集在掌子面附近。在粉塵的初速度和風速的作用下，爆破粉塵迅速擴散，最遠擴散距離約為30 m。

（2）爆破10～100 s內，粉塵在氣流作用下逐漸擴散，并且在重力作用下發生沉降，導致巷道內粉塵濃度變得稀疏。未發生沉降的顆粒在整個巷道內隨機分布。

（3）隨著時間的推移，在100 s左右整個巷道粉塵濃度逐漸減少。粉塵在隧道壁面附近存在明顯的粉塵聚集現象。

4.3 不同粒徑粉塵沿著隧道分布規律

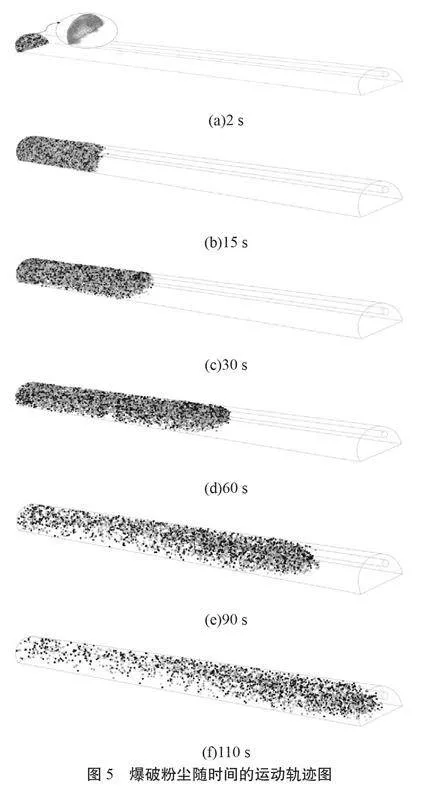
Rosin-Rammler分布函數是描述粉塵粒徑分布最權威的模型和方法[8-9]。該文采用離散相模型，粒徑滿足R-R分布。不同粒徑顆粒隨時間的運動軌跡如圖5所示。

（1）爆破產生的大顆粒粉塵在掌子面附近區域沉降，而小顆粒粉塵大部分隨著壓入的氣流流動到整條隧道中。

（2）顆粒的粒徑越大，其沉降速度越快，沉降時間越短。36 μm以上的粉塵顆粒大部分在距掌子面30 m范圍內就已發生沉降，12～31 μm范圍內有小部分粉塵顆粒能夠沉降，在通風100 s后粉塵已經運移到隧道出口，隧道內均為18 μm以下的粉塵顆粒。

（3）隨著時間的推移，留存在隧道空間中的粉塵顆粒直徑逐漸減小，而且總體粉塵顆粒數量也逐漸減少。粉塵顆粒擴散到30 m、60 m和100 m分別需要10 s、40 s和100 s左右的時間。

4.4 數值模擬結果驗證

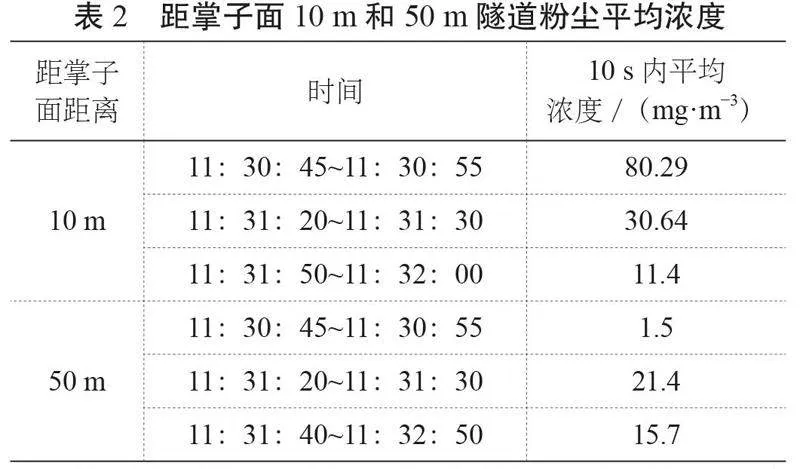
該實驗使用了CCZ3000直讀式粉塵濃度測量儀測量隧道爆破后的瞬時揚塵濃度。在隧道粉塵濃度監測工作之前，首先利用測距設備進行測量，后對監測點進行標記，在距掌子面10 m和50 m分別布置兩臺儀器。在爆破前儀器開始工作，直到工作人員可以進入工作面關閉儀器。儀器所測得斷面數據如表2所示。

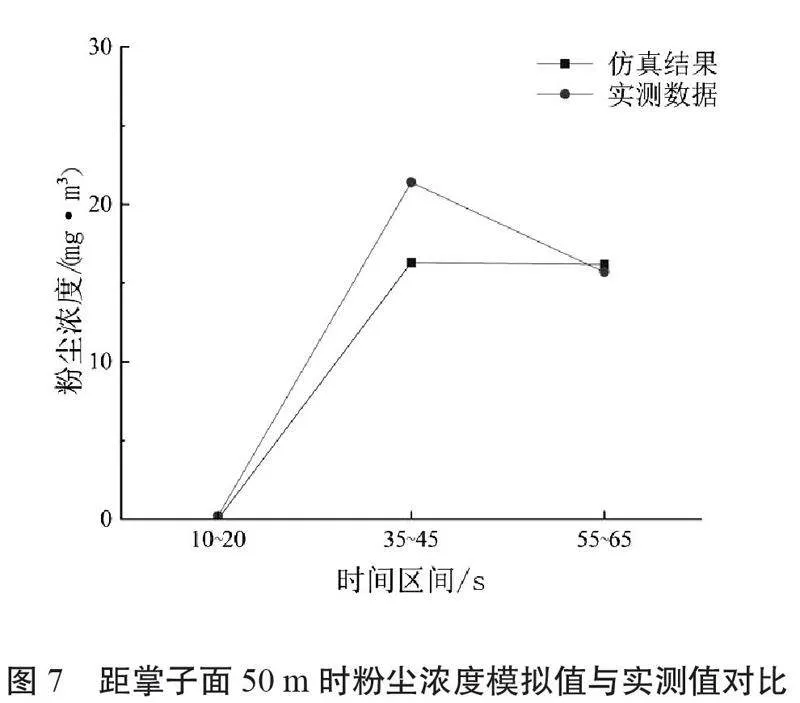
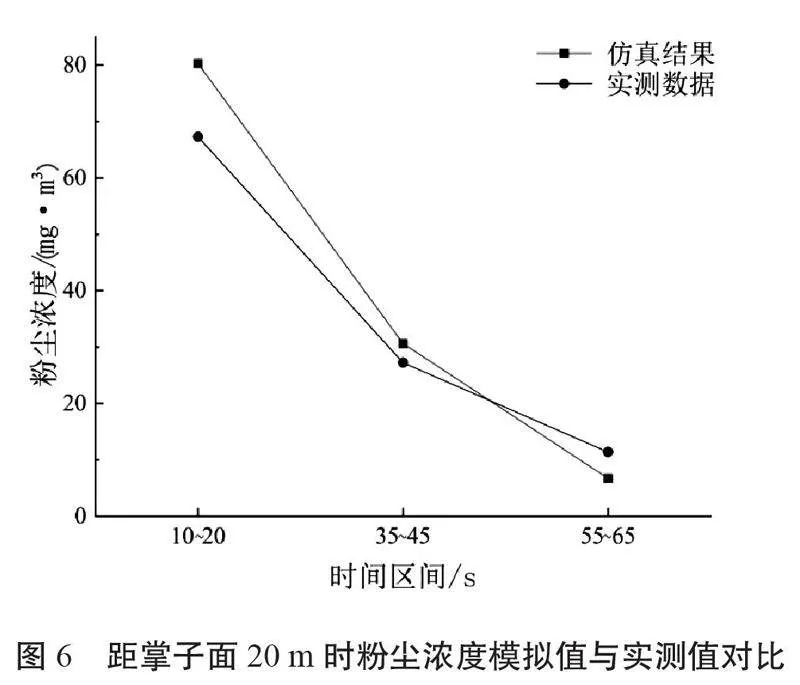
為了驗證數值模擬結果的準確性，優化模擬參數的設置，將斷面粉塵濃度的模擬結果與實測的實驗數據進行對比，對比結果如圖6和圖7所示。

從圖6和圖7可以看出，粉塵濃度數值模擬結果在趨勢上與實測數據基本一致，誤差在可控范圍內，從圖中得出誤差較小，模擬結果可信。但兩者的數值還存在一定的誤差，這主要是由于仿真參數設置與實際工程背景條件仍然存在一定差異，并且現場干擾的因素也會對實測數據的結果造成一定的影響。對比分析表明，該文所用的數值模擬方法準確可信。

5 結論

該研究在氣固兩相流理論研究和空氣流場模擬的基礎上，利用Fluent軟件對隧道施工中爆破粉塵濃度變化和粒徑分布進行了分析模擬。并將模擬結果與實測數據進行了對比分析。可得出以下結論：

（1）隧道掘進爆破后，爆破粉塵會在沖擊波及高壓氣體的作用下高速噴入隧道，并隨風流擴散至隧道口。揚塵濃度隨著時間的推移逐漸降低。粉塵濃度在6～40 s內下降最快，40 s后開始緩慢下降。在爆破100 s后，巷道內大部分區域粉塵濃度降到10 mg/m3以下。

（2）在風流作用下，粉塵顆粒會沿隧道沉降、被捕獲或排除。大顆粒首先在重力作用下迅速沉降，而小顆粒則在隧道內隨機流動，并隨著氣流繼續向前擴散。

（3）仿真結果表明，爆破粉塵量大，自然條件下難以降低。在距工作面0～46 m粉塵濃度最大，在此范圍內采取除塵措施，如布置水霧降塵設備，可以得到理想的除塵效果，除塵措施宜在爆破后10～100 s快速實施。

參考文獻

[1]YU H， CHENG W， XIE Y， et al. Micro-scale pollution mechanism of dust diffusion in a blasting driving face based on CFD–DEM coupled model[J]. Environmental Science and Pollution Re-search， 2018（22）： 21768-21788.

[2]林榮漢，李國清，胡乃聯，等.高海拔掘進巷道混合式通風參數優化[J].中國礦業，2017（4）：121-125.

[3]王應權.長大鐵路隧道施工通風方案選擇及優化[J].地下空間與工程學報，2015（S1）：359-366.

[4]曹正卯，劉曉，牛柏川.高海拔公路隧道施工期粉塵運移特性研究[J].地下空間與工程學報，2019（3）：927-935.

[5]謝全敏，李文松，黃昆，等.隧道曲率半徑對噴漿粉塵遷移規律的影響研究[J].武漢理工大學學報，2023（10）：91-97.

[6]PE?REZ K， TORO N， GA?LVEZ E， et al. Environmental， economic and technological factors affecting Chilean copper smelters—A critical review[J].Mater Res Technol， 2021（15）： 213–225.

[7]蔣仲安，陳記合，王明，等.卸礦站粉塵濃度影響因素的數值模擬研究[J].煤炭學報，2018（S1）：185-191.

[8]胡志偉，畢建乙，王海東.斜溝煤礦長距離掘進面爆破粉塵運移規律研究[J].中國礦業，2019（S2）：340-345.

[9]龔曉燕，莫金明，薛馨禹，等.分形特征對掘進通風粉塵分布和沉降規律影響分析[J].煤炭技術，2017（9）：112-114.