地震輸入方向對某公路斜梁橋抗震性能影響研究

摘要 為研究地震輸入方向對橋梁抗震性能的影響，文章借助有限元軟件建立了某公路一聯3跨20 m斜交簡支梁抗震分析的有限元數值模型，計算結果表明：地震輸入方向對橋墩受力影響較大，最不利地震輸入方向受墩臺偏轉角度最大的橋跨控制，在文章所選取的橋墩和樁基尺寸及配筋條件下，抗震性能能夠滿足規范要求。

關鍵詞 橋梁工程；地震輸入方向；斜梁橋；抗震性能

中圖分類號 U442 文獻標識碼 A 文章編號 2096-8949（2024）17-0013-04

0 引言

近年來，全國高速公路建設實現了跨越式發展，橋梁設計方法和施工工藝得到不斷進步與提高，橋梁型式和規模決定了高速公路的建設難度和施工工期。目前橋梁建設通常以常規裝配式簡支梁為主，完備的預制梁場和成熟的架梁工藝能夠大幅度縮減建設工期，當前主線橋梁常用的跨徑類型包括16 m、18 m、20 m、25 m、30 m和40 m，結構形式包括預制矮T梁、T梁和箱梁。西部山區地面線形變化大、地形陡峭，常規橋跨徑多以25 m、30 m和40 m為主，中部和沿海平原地區，受地形條件限制，通常采用技術經濟指標較好的中小跨徑矮T梁形式。與早期橋梁建設中應用較多的空心板相比，矮T梁的投入應用不僅解決了空心板承載能力低、后期裂紋多等問題，同時也避免了空心板鉸縫后期運營過程中所出現的一系列質量問題，目前矮T梁在橋梁建設中得到了一定規模的應用。

路線走向決定橋梁的整體布置，對于主線橋而言，采用以直代曲的裝配式簡支梁形式通常能夠滿足路線平縱指標要求，因此斜梁橋在梁式橋中占有重要地位。劉聰[1]基于剛性橫梁法研究了斜交梁空間受力及分配情況；劉迪愛等[2]結合橫向分布系數基本概念，對剛性橫梁法和比擬正交異性板等方法進行了對比分析，并證明了梁格法分析的可靠性；龍佩恒等[3]基于ANSYS有限元軟件，構建了斜交梁橋實體有限元模型，對全橋受力與裂縫成因進行了詳細分析；李廣[4]基于橋梁荷載試驗方法，對濟南市大辛河簡支斜交梁橋結構的運營狀態進行了評估，并給出了加固方案；曾天寶等[5]探討了支座布置形式對斜梁橋下部結構受力的影響。目前關于斜梁橋的研究文獻主要集中在荷載橫向分布、靜力分析、施工及加固分析，對于抗震性能方面的研究相對較少。該文以應用較為廣泛的矮T梁為分析對象，結合某公路3跨20 m斜交梁實橋案例，借助有限元軟件，重點對地震輸入方向進行了分析探討，然后結合最不利地震輸入方向對下部結構強度進行了驗算分析，分析方法和計算結果可為類似結構提供參考。

1 分析方法介紹

反應譜法通過建立結構的加速度-頻率響應函數，對結構在地震作用下的反應進行評估。它是一種時程分析方法，通過輸入合適的地震動，模擬結構在地震中的動力響應，并獲得結構的最大位移、加速度、剪力等重要指標，以評估結構的抗震性能和結構的安全性。反應譜法的核心思想是共振原理。當結構自身固有頻率與輸入地震動的卓越頻率保持一致時，結構的動力反應將會增大。反應譜法將實際地震動分解為含有一定卓越頻率的復雜波，施加到某一單自由度的結構體系上，以獲得結構的周期-地震響應（絕對加速度、相對速度及相對位移等）曲線，即反應譜。

在實際工程中，經常采用輸入大量不同特性的地震動，以得到與其對應的反應譜。再采用平均和光滑的數理統計方法，最終得到用于規范抗震設計的反應譜，用于后續抗震分析與設計應用。這種方法因其可描述客觀存在因素的隨機性，在包括土木工程在內的多個工程領域得到了廣泛應用，其主要優點包括：相對于底部剪力法更加精確，能夠考慮結構的前幾階振型；相比時程分析法而言，計算也比較簡單。

反應譜理論考慮了結構動力特性與地震動特性之間的動力關系，通過反應譜計算由結構動力特性（自振周期、振型和阻尼）所產生的共振效應，但其計算公式仍保留了早期靜力理論的形式。地震時結構所受的最大水平基底剪力，即總水平地震作用，可以通過如下公式計算：

FEK=kβ（T）G （1）

式中，k——地震系數；β（T）——加速度反應譜Sa（T）與地震動最大加速度a的比值，它表示地震時結構振動加速度的放大倍數；G——重力荷載（N）。

采用反應譜法建立抗震分析模型時，主要步驟包括：定義材料和截面、建立模型、指定邊界、施加荷載、設立分析工況、查看結果和后處理等。反應譜分析工況通常需要兩個正交方向的地震輸入，地震輸入角度是抗震分析時需要關注的重要參數，一般是按照建模坐標系的X和Y兩個方向進行輸入，模態組合控制一般用CQC進行控制。

2 實橋案例

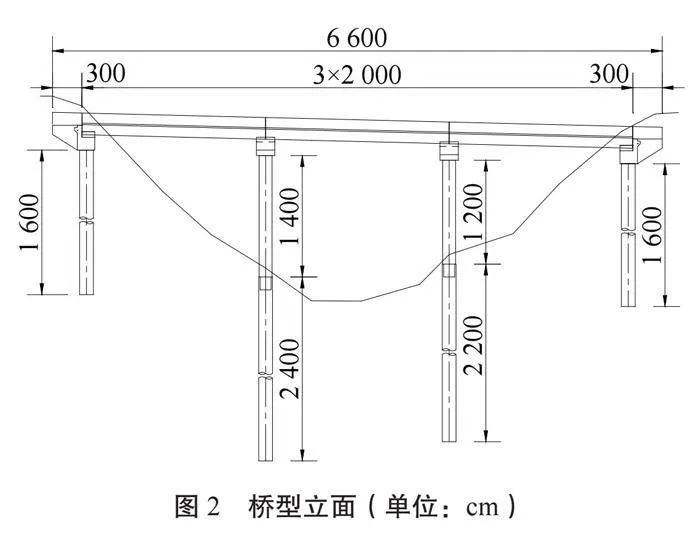
某公路上部結構采用3跨20 m斜交矮T梁方案，矮T梁梁高110 cm，頂板厚度為16 cm，邊梁外懸臂長度為55 cm，中梁懸臂長度為50 cm，橋面鋪裝采用8 cm厚C40混凝土+10 cm厚瀝青混凝土的組合形式。橋梁主要技術標準：設計速度為80 km/h，地震動加速度為0.20 g，抗震設防烈度為Ⅷ度，荷載等級為公路-Ⅰ級，防撞護欄等級為SS級，設計使用年限為100年。橋梁前2跨主要位于緩和曲線范圍內，第3跨位于半徑為90 m的圓曲線范圍內，按照以直代曲對預制梁進行布置，相比于現澆梁可實現全橋結構的輕質化設計。單跨范圍內主梁均采用7片預應力混凝土矮T梁形式，混凝土等級為C50，鋼絞線規格選用9-φ15.2和10-φ15.2，墩柱和樁基混凝土等級分別為C35和C30，混凝土和鋼絞線材料性能指標按照《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTG 3362—2018）進行選取[6]。該橋主梁標準橫斷面和橋型立面圖分別如圖1和圖2所示：

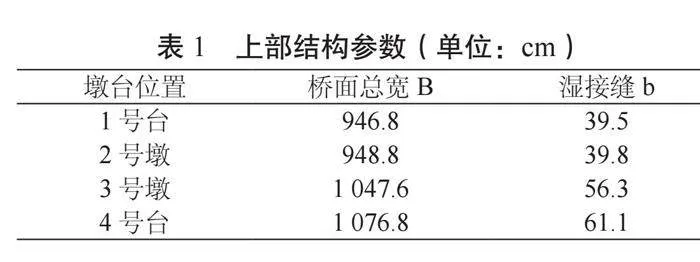
將小樁號至大樁號方向的墩臺依次編號為1至4，圖1中橋面總寬B和濕接縫b選取的參數見表1所示：

3 有限元模型

3.1 支座選取

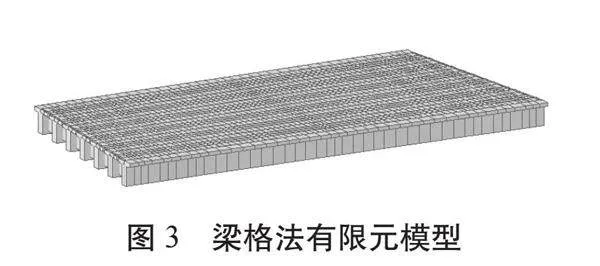
考慮斜梁橋單梁分析與實際狀態的差異，同時便于后續抗震分析的需要，按照梁格法對上部結構進行建模；第3跨橫向橋面較寬，選取該跨進行分析以確定支座規格。第3跨梁格法的有限元模型建立如圖3所示：

按照活載橫向分布基本概念，分別在小樁號支座、1/4跨、跨中、3/4跨和大樁號支座位置截面定義車道，并按照橫向移動進行分析，分別提取7片梁剪力F1、F2、F3、F4、F5、F6、F7，則任一截面處第n片梁的荷載橫向分布系數為Fn/（F1+F2+F3+F4+F5+F6+F7）。在得到橫向分布系數的基礎上，可進行單梁分析，進而得到標準組合下的支座反力，其最大值為580 kN，按照富裕度10%進行支座選取，則2號和3號墩板式支座的規格為GBZJ250×300×52 mm，1號和4號臺滑板橡膠支座規格為GBZJH250×300×54 mm[7]。

3.2 抗震分析有限元模型

為適應地面線形變化，確保樁基基本埋入至地面線以下，雙柱式橋墩采用高低墩形式，低墩樁頂系梁與高墩進行連接。上部結構均采用梁格法進行建模，支座均采用線彈簧單元模擬，其中橋墩處板式支座縱橫向剛度與剪切模量Gd、剪切面積Ar和橡膠厚度t有關，縱橫向剛度可由k1=GdAr/t計算，其數值取2 432 kN/m，所有支座的豎向剛度均取無窮大值，而滑板橡膠支座的縱橫向剛度則取為0。

樁基與周圍土體的相互作用按照《公路橋涵地基與基礎設計規范》（JTG 3363—2019）中的M法進行計算[8]，地層主要為堅硬的密實粉質黏土，靜力計算中地基土比例系數m取30 000 kN/m4，抗震分析時按照2.5倍進行考慮。土彈簧剛度可由以下公式計算：

k1=ab1mz （2）

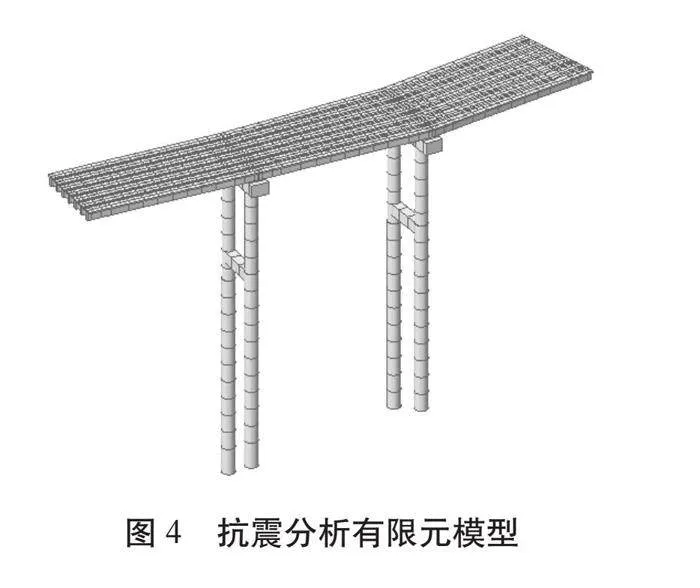
式中，a——樁徑（m）；b1——樁的計算寬度（m），取2.25 m；z——地基土彈簧位置至地平線深度（m）。所建立的抗震分析有限元模型如圖4所示：

4 地震輸入方向分析

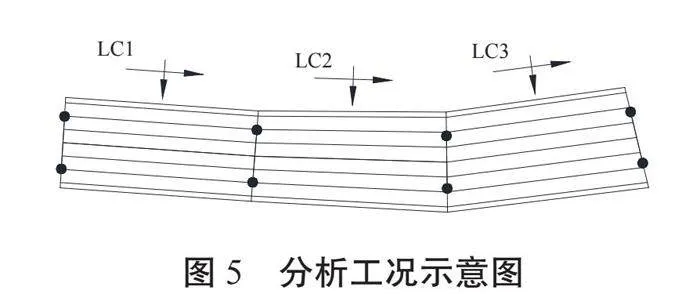
地震輸入方向的確定對于結構抗震驗算至關重要，根據《公路橋梁抗震設計規范》（JTG/T 2231-01—2020）[9]相關要求，曲線橋需對與多個相鄰橋跨中心連線正交的地震輸入方向進行對比分析，以確定最不利的地震輸入方向。結合該橋平面布置情況，該次主要分析三種地震輸入方向，如圖5所示。其中，LC1為第一跨順、橫橋向分析工況；LC2為第二跨順、橫橋向分析工況；LC3為第三跨順、橫橋向分析工況。

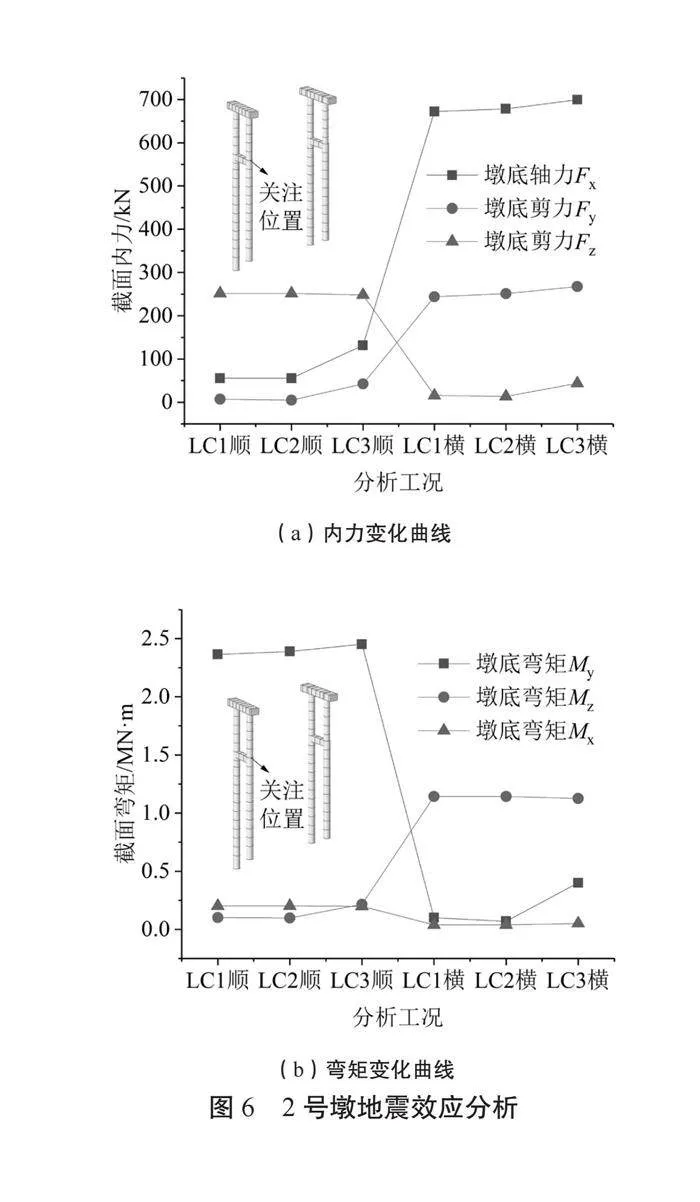
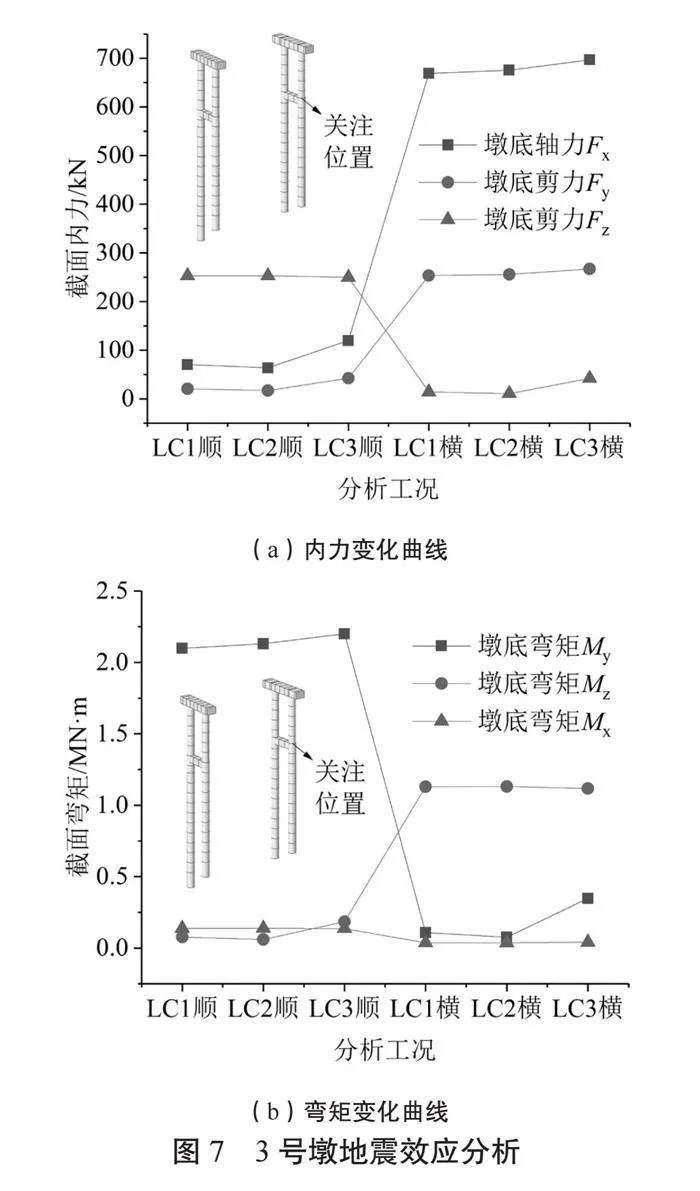
采用反應譜分析方法，依次對三種工況進行分析。由于E1和E2地震作用下的高墩和低墩受力情況基本類似，為便于分析，分別選取2號墩和3號墩的低墩墩底截面為關注對象，計算得到E1地震的軸力、剪力和彎矩效應，分別如圖6和圖7所示。

根據計算結果，可以得到以下結論：

（1）對于橋墩截面內力而言，墩底剪力在同方向地震作用下的表現為最大，但總體而言，三種工況下的墩底順橋向和橫橋向在任意方向地震作用下的剪力水平，明顯小于橫橋向地震作用下的墩底剪力。以2號墩為例，墩底最大剪力為267.5 kN，最大軸力為699.6 kN。通過對比2號、3號墩的軸力變化情況，在LC3順橋向、橫橋向地震工況下墩底軸力和剪力均為最大，截面內力受LC3橫橋向地震作用下的軸力控制。

（2）三種工況下任意方向沿橋墩軸線的彎矩水平較小，基本可以忽略。在LC3順橋向地震作用下，2號、3號墩順橋向彎矩均達到最大值，分別為2 450.9 kN·m、2 200.2 kN·m，同時在LC3順橋向地震作用下，2號、3號墩橫橋向彎矩也較大，但整體水平明顯小于順橋向彎矩。

（3）第1跨、第2跨和第3跨的墩臺偏轉角度分別為1.1°、5.4°和12.5°，地震作用下整聯橋墩墩底截面軸力和彎矩均受墩臺偏轉角最大的橋跨控制，橋墩和樁基抗震驗算應選擇LC3為不利工況。

5 抗震驗算

該橋橋位地震烈度較高，2號、3號橋墩和樁基配筋分別為36根直徑為25 mm和28 mm的熱軋帶肋鋼筋，強度等級為HRB400。有限元分析時墩樁混凝土采用塑性損傷本構、鋼筋采用雙折線彈塑性本構，選擇LC3順橋向和橫橋向地震工況，與永久作用進行地震驗算的偶然組合[9]，考慮墩樁為偏心受壓結構，取2號、3號低墩軸力進行E1地震強度驗算，取對應樁基進行E2地震強度驗算。由此計算得到2號、3號低墩墩底的軸力分別為2 133.2 kN、2 245.5 kN，對應容許軸力分別為4 120.6 kN、4 430.1 kN，對應樁基最大計算彎矩分別為5 460.3 kN·m、5 270.6 kN·m，等效屈服抗彎能力均為6 150.4 kN·m，橋墩強度安全系數為1.93，樁基能力/需求為1.13，均滿足規范要求，表明橋墩和樁基均處于彈性狀態。

6 結束語

該文借助有限元軟件建立了某公路一聯3跨20 m斜梁橋抗震分析的有限元數值模型，結合相關規范選取典型地震輸入方向，對斜梁橋抗震性能進行了對比分析，得到了最不利地震輸入方向，計算結果表明最不利地震輸入方向受墩臺偏轉角度最大的橋跨控制。最后基于最不利地震輸入方向對橋墩和樁基進行了抗震驗算。

參考文獻

[1]劉聰.基于剛性橫梁法的簡支斜梁橋主梁影響面研究[J].中外公路，2019（5）：107-110.

[2]劉迪愛，袁建偉，萬航.簡支斜T梁橋荷載橫向分布研究[J].公路與汽運，2019（1）： 133-135+139.

[3]龍佩恒，張廣達，宋浩.鋼筋混凝土簡支斜梁橋裂縫成因分析[J].市政技術，2016（5）：43-47.

[4]李廣.基于荷載試驗的簡支斜梁橋結構狀態評定與加固技術研究[D].哈爾濱：哈爾濱工業大學，2018.

[5]曾天寶，黃筱淇.支座形式對連續折線形斜梁橋力學行為的影響[J].城市道橋與防洪，2021（1）：88-90+120+12.

[6]公路鋼筋混凝土及預應力混凝土橋涵設計規范：JTG3362—2018[S].北京：人民交通出版社，2018.

[7]公路橋梁板式橡膠支座：JT/T 4—2019[S].北京：人民交通出版社，2019.

[8]公路橋涵地基與基礎設計規范：JTG 3363—2019[S].北京：人民交通出版社，2019.

[9]公路橋梁抗震設計規范：JTG/T 2231—01—2020[S].北京：人民交通出版社，2020.