把控知識歸納過程，統籌單元教學節奏

新課標持續深化，轉變了以往重視課時教學設計的狀況，倒逼單元作為課程最小組織單位，形成結構化單元教學設計，實現學生核心素養的有效培養。在單元教學設計中，需體現整合化、結構化等特點，與數學核心素養培養具有一致性目標。一個單元需要安排多個課時，教師可以總結歸納單元課時知識點，并加以整合，把握單元教學節奏，由此中心向外拓展，構建數學知識體系，鍛煉學生數學思維能力的同時提升其數學核心素養。本文以人教版五年級上冊第六單元“多邊形的面積”為例，歸納總結各個課時的知識點，找出各個知識點之間的聯系，加以整合，提高單元教學實效性。

一、教材分析

“多邊形的面積”作為“圖形和幾何”領域的重要組成部分，其安排在人教版五年級上冊第六單元，包含“平行四邊形的面積”“三角形的面積”“梯形的面積”“組合圖形的面積”四個內容。在此之前，學生已經掌握了長方形、正方形基本圖形面積的計算方法，為“多邊形的面積”學習奠定了基礎。此外，“多邊形的面積”單元學習為圓的面積、立體圖形的表面積以及體積等知識點的學習奠定基礎。

二、學情分析

“多邊形的面積”為五年級課程，學生在此之前已經掌握了基本圖形面積的計算公式，同時也掌握了數格子法、割補法，使學生能夠快速掌握本單元知識點。基于小學生年齡特征，學生思維能力處于快速發展階段，教師需采用多種教學方法引導學生實現思維的過渡，即從具象邏輯思維過渡到抽象邏輯思維。小學生擁有一定的空間想象力，但未形成概念，對圖形的拼接轉化難以想象，無法完成多邊形面積計算公式的推導。本單元學習旨在幫助學生掌握知識歸納的方法，基于已學知識點探索新知，逐漸完善學生的知識體系。

三、教學目標

1.運用轉化思想：學習掌握數格子法、割補法等圖形拼接方法，完成圖形間轉化，從而推導出多邊形面積計算公式，并利用面積計算公式成功計算多邊形面積。

2.發展空間觀念：通過觀察、分析、操作等實現空間觀念的有序發展，提高問題解決能力。

3.培養探索創新精神：通過不斷地探索掌握單元新知，并將數學與生活相聯系，實現探索創新精神的培養。

四、教學重難點

教學重點：學生掌握數格子法、割補法等方法，將復雜的圖形轉化為簡單的圖形，利用簡單圖形的面積計算公式，加以組合，從而計算出復雜圖形的面積。

教學難點：培養學生多角度思考問題的能力以及轉化思想；理解多邊形面積計算公式推導過程。

五、教學過程

（一）導入環節

1.回顧知識點

出示課件（長方形、正方形的圖片），讓學生回答長方形和正方形的面積計算公式。

教師：同學們，你們還記得長方形、正方形的面積計算公式嗎？

學生A：長方形的面積計算公式：長方形面積=長×寬。

學生B：正方形的面積計算公式：正方形面積=邊長×邊長。

教師：在學習長方形、正方形面積時，采用什么方法得到的呢？

學生A：數格子方法。

教師再次出示平行四邊形圖片。

教師：同學們，我們該如何計算平行四邊形的面積呢？

學生A：可以采用數格子方法。

學生B：也可以采用割補法。

教師：是的，我們可以利用以往學過的方法計算多邊形的面積。

（設計意圖：“溫故而知新”是課堂教學的重要內容，通過對已學知識點的回顧，能夠再次鞏固以往知識點，而且為新知的探索奠定了基礎。）

2.新課導入

教師：同學們觀察這兩個花壇（長方形花壇、平行四邊形花壇），誰能說一下兩者的面積大小。

學生A：兩個花壇的大小一致。

學生B：不對，長方形花壇面積大于平行四邊形花壇面積。

學生C：不是這樣的，是平行四邊形花壇面積大于長方形花壇面積。

教師：哦，同學們都有著不同的見解，那我們該怎么驗證你們的猜想呢？如何計算平行四邊形花壇的面積呢？

（設計意圖：利用生活中的實物，降低數學知識的抽象感，便于學生將數學與生活相聯系，從而激發學生探究數學知識的欲望。）

（二）動手實踐——平行四邊形面積計算

1.數一數

教師：那同學們知道長方形花壇面積的計算方法嗎？

學生A：長方形花壇面積的計算方法為長×寬。

教師：那大家知道如何計算平行四邊形花壇的面積嗎？

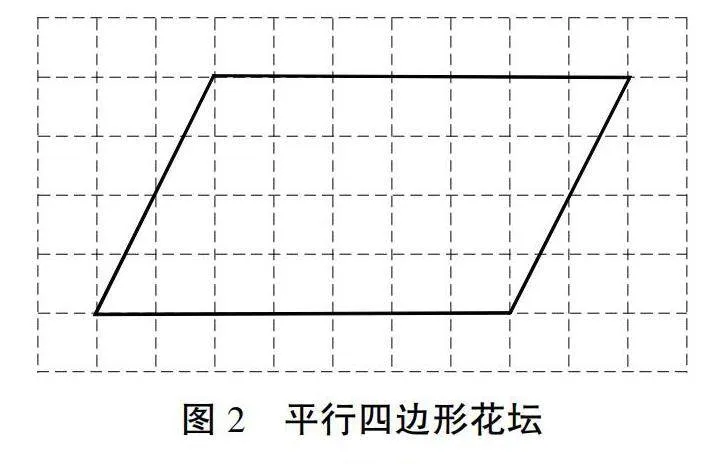
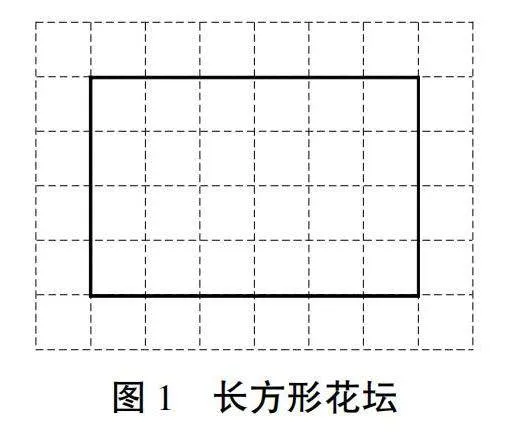
學生B：可以采用數格子方法，以長方形花壇為基礎，長為6m，寬為4m；按照數格子方法將長方形花壇按比例畫出相應的小方格，一個小方格子的邊為1m（見圖1）；再將平行四邊形花壇的邊長、角度等進行測量，其中不滿一格都按照整格計算，由此可獲得平行四邊形面積（見圖2）。

教師：通過這位同學的數格子方法計算出的平行四邊形花壇面積，和長方形花壇面積相比較，兩者的大小如何？

學生（異口同聲）：長方形花壇面積和平行四邊形花壇面積相等。

教師：那我們可以采用其他方法計算平行四邊形面積嗎？

學生C：可以采用割補法計算。

教師：那思考一下，數格子方法可以廣泛運用在多邊形面積的計算中嗎？

學生D：數格子方法并不適用于任何圖形面積的計算，如果說圖形過于復雜，則不適合用數格子的方法。

2.剪一剪，拼一拼

教師：有同學提議利用割補法實現平行四邊形面積的計算。平行四邊形是可以隨意切割的嗎？

學生A：應該是可以隨意切割的吧。

學生B：不能隨意切割。

教師：那我們動手操作一下，選擇切割線，把平行四邊形切割后，自行計算一下平行四邊形。

學生劃分為多個小組，在小組內進行平行四邊形的切割、平移操作。

教師：哪個小組學生計算出平行四邊形的面積了？

學生A：我們小組算出來了。

教師：其他小組有沒有算出來呢？如果沒有那我們請這組成員來分享。

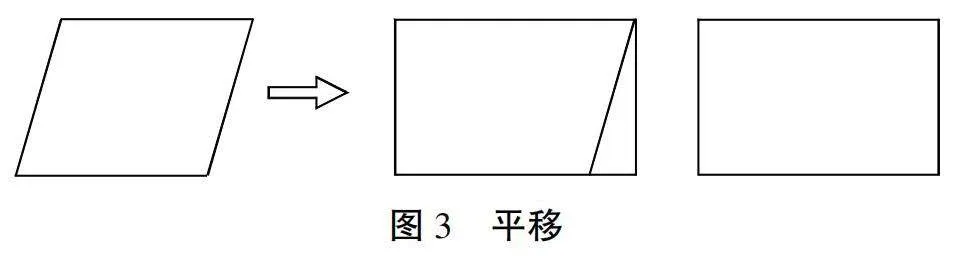
學生A：我們先以平行四邊形的對角線為切割線，但得到的圖形還是平行四邊形，說明沿著平行四邊形對角線切割，無法計算出平行四邊形面積。而以平行四邊形的高作為切割線，將直角三角形部分平移至平行四邊形的另一側，確保平行四邊形的斜邊和直角三角形的斜邊重合，形成新的圖形——長方形。并利用長方形面積計算公式進行計算，得到長方形面積值，也就是平行四邊形的面積（見圖3）。

學生B：我們小組也算出來了，以平行四邊形上下兩條邊的中點作一垂線，并沿著中線切割，將平行四邊形的一半向右平移，確保平行四邊形兩個斜邊重合，得到長方形。

教師：同學們，你們知道這種切割、平移的過程體現了哪種思想嗎？

學生紛紛搖頭。

教師：將平行四邊形轉變為長方形的過程體現了轉化思想，這種思想在多邊形面積計算中十分重要。

教師：同學們，我們再來觀察一下長方形和平行四邊形，你能看出兩者的關系嗎？

學生A：長方形的長等于平行四邊形的底。

學生B：長方形的寬等于平行四邊形的高。

教師：那誰來說一下平行四邊形面積的計算公式呢？

學生C：因為知道長方形的面積計算公式，也知道長方形長、寬和平行四邊形底、高的關系，所以平行四邊形的面積=底×高。

教師：這位同學說得不錯，平行四邊形的面積=底×高。（板書：S=a×h，教師告知學生每個字母代表的含義：S為面積，a為底，h為高）

教師：在推導平行四邊形面積計算公式的過程中，除了長方形的長、寬與平行四邊形底、高相等的特征外，還有哪些特征呢？

學生A：切割后圖形的面積與原平行四邊形面積相等。

學生B：拼成長方形的面積與原平行四邊形面積相等。

（三）思考應用——三角形和梯形面積計算

1.三角形面積計算

教師：我們學習了平行四邊形面積的計算方法以及計算公式的推導，那我們應如何計算三角形面積呢？

學生A：可以采用數格子的方法計算。

學生B：也可以采用割補法計算。

學生C：不能采用數格子方法，如果是直角三角形、等腰三角形等特殊三角形，可以采用數格子方法，如果是普通三角形，應用數格子方法比較煩瑣，最終計算的面積不準確。

教師：那我們采用割補法就可以了嗎？

學生D：我覺得采用割補法也存在和數格子方法一樣的情況，不利于三角形面積的計算。

教師：那我們該如何計算三角形的面積呢？

教師為學生準備多個三角形。

學生A：我采用的拼接法，用筆將三角形的形狀位置描畫出來，并將此三角形旋轉180°，形成平行四邊形，即平行四邊形面積等于兩個三角形的面積，根據平行四邊形面積計算公式反推三角形面積計算公式，即三角形面積=底×高÷2。（板書：S=a×h÷2。）

教師：同學們，按照平行四邊形面積計算公式，通過動手操作、思考分析推導出三角形面積計算公式，那我們總結一下，三角形面積計算公式通過什么方法得到的呢？

學生C：利用的是轉化思想，三角形通過拼接、割補、平移、旋轉等操作，轉化為以往學過的圖形，即長方形、平行四邊形；并根據以往圖形面積計算公式反推出三角形面積計算公式，同時要驗證一下特殊三角形、普通三角形是否都適用三角形面積計算公式。

（設計意圖：在推導三角形面積公式時，教師依舊引導學生思考，利用已經掌握的割補法、拼接法等圖形轉化方法，將未知的三角形面積知識轉化為熟悉圖形的面積計算公式，從而獲得三角形面積計算公式。整個學習過程，鍛煉學生獨立自主運用轉化思想的能力，促使學生深化自身的知識歸納能力。）

2.梯形面積計算

教師：同學們，讓我們看一下這個圖形，大家認識嗎？（出示梯形）

學生：這是梯形。

教師：我們已經學習了長方形面積、平行四邊形面積以及三角形面積的計算公式，也掌握了面積計算公式的推導過程，讓我們思考一下，梯形的面積該如何計算呢？

（教師給予學生一定的思考時間）

學生A：沿著梯形的對角線切割，形成兩個三角形，計算兩個三角形的面積，從而推導出梯形面積計算公式。

學生B：可以采用拼接法，將梯形旋轉180°，形成一個平行四邊形，并依據平行四邊形面積計算公式推導出梯形面積計算公式。

學生C：可以將梯形切割為一個長方形和兩個直角三角形，通過計算長方形面積、兩個直角三角形面積，從而推導出梯形面積計算公式。

教師：同學們分別說了自己的想法，那我們分小組驗證一下你們的猜想是否正確。

小組A：以對角線切割梯形，梯形的上底、下底分別是兩個三角形的底，根據三角形面積=1/2底×高；梯形面積=兩個三角形面積之和=1/2上底×高+1/2下底×高=1/2（上底+下底）×高。

小組B：原梯形旋轉180°后，獲得一個平行四邊形，依據平行四邊形面積公式，即平行四邊形面積=底×高；平行四邊形由兩個梯形組成，其中平行四邊形的底是梯形上底、下底的和，所以梯形面積=1/2平行四邊形面積，進而推導出梯形面積計算公式=1/2底×高=1/2（上底+下底）×高。

教師板書：S=1/2（a+b）h。

教師：經過同學們的猜想，動手驗證，從而推導出了梯形面積計算公式。

（設計意圖：學生在推導平行四邊形面積計算公式時，掌握了割補法、拼接法等方法，并在三角形面積、梯形面積學習中，能夠獨立自主地完成面積計算公式推導，提高學習效果。）

（四）作業設計

作業一：平行四邊形面積計算的相關習題。

作業二：三角形面積計算的相關習題。

作業三：梯形面積計算的相關習題。

作業四：出示一個組合圖形，讓學生獨立自主完成面積計算。

六、教學反思

在“多邊形面積”教學中，教師不僅要注重單一課時內容的講解，還要將單元內多個課時加以整合，提煉多個課時的關聯知識點，加強單元內各個課時的聯系，提高單元教學效果。“多邊形面積”單元教學中，教師側重于學生獨立自主、知識歸納總結等綜合能力的培養，轉變自己的角色定位，提出相應的問題，讓學生聯想、分析、驗證、總結，逐漸完成教學知識點的歸納，由此可加深學生對“多邊形面積”知識點的理解。此外，教師在教學中給學生留有充足的探索時間，學生通過知識的自我探索、歸納進一步扎實掌握數學知識。值得注意的是，教師要掌握好單元教學節奏，引導學生找到單元教學的連接點，增強單元教學實效性。

（作者單位：福建省龍巖體育運動學校）

編輯：陳鮮艷