過冷大水滴運動和撞擊特性數值模擬

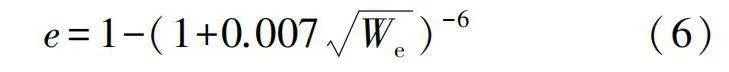
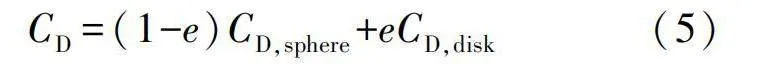
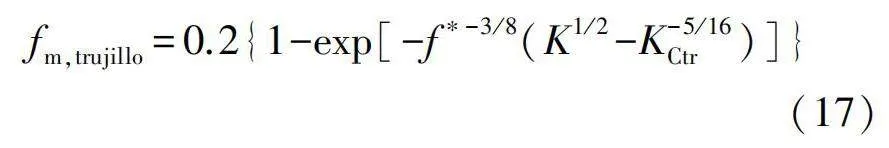
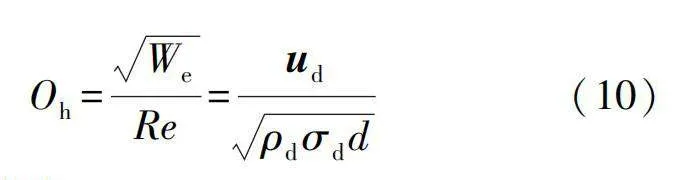
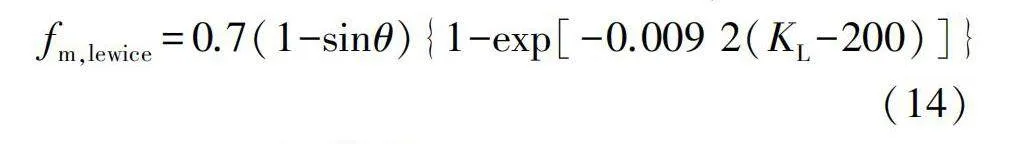
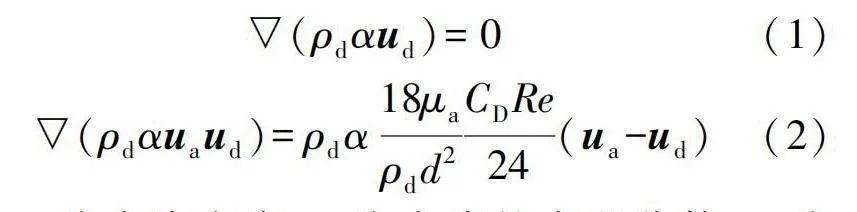
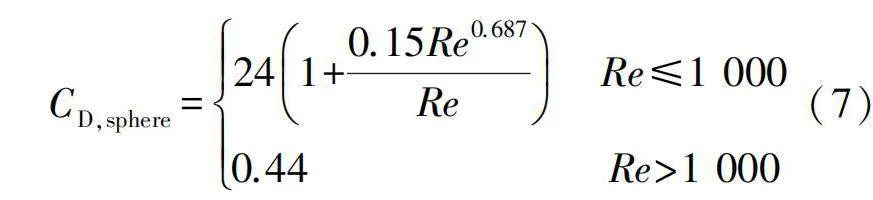
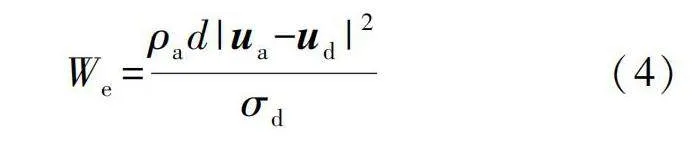
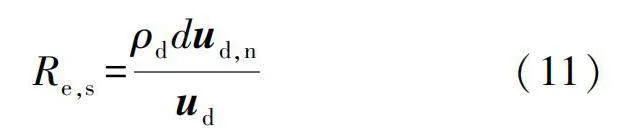
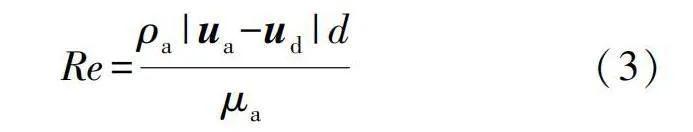
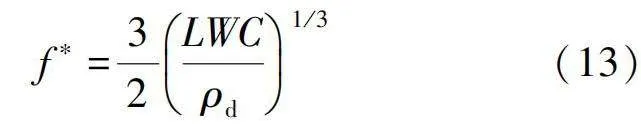
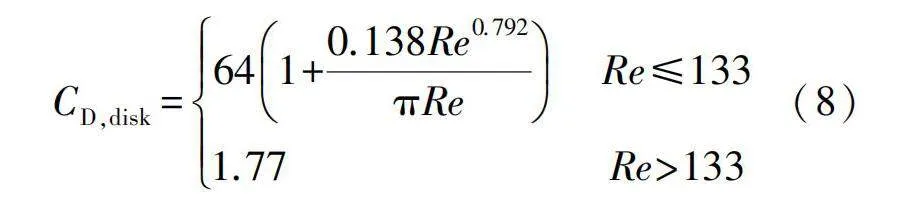
摘 要：為了更準確地模擬過冷大水滴在結冰部件中的撞擊特性，基于LEWICE模型和Trujillo模型的過冷大小滴撞擊模型，以NACA23012翼型為研究對象，通過Fluent軟件的二次開發功能，考慮大水滴運動中變形以及撞擊中反彈/飛濺的影響，對過冷大水滴的運動和撞擊特性進行數值模擬，并將計算結果與NASA的試驗數據進行對比。結果表明：當過冷水滴的MVD值較大時，相比于LEWICE模型和Trujillo模型，結合兩個模型計算得到的翼型表面局部水收集系數的計算結果和撞擊范圍都更貼合試驗數據，絕大部分計算結果和試驗數據的誤差在10%以內；MVD值越大，局部水收集系數值的計算結果和試驗值越貼近。

關鍵詞：過冷大水滴；數值模擬；變形；反彈；飛濺

中圖分類號：TP391.9 文獻標志碼：B 文章編號：1671-5276（2024）04-0140-06

Numerical Simulation of Motion and Impingement Characteristics of Supercooled Large Droplets

LI Zhonghui， LI Shiming， LIU Lei， YU Dongyin

（College of Energy and Power Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract：In order to more accurately simulate the impingement characteristics of supercooled large droplets on frozen parts， based on LEWICE model，Trujillo model and two SLD impingement models， taking NACA23012 airfoil as the research object and with the secondary development function of Fluent software， conducts the numerical simulation on the motion and impingement characteristics of SLD in consideration of the influence of deformation during movement and rebound/splash during impingement. The calculated results are compared with the experimental data of NASA. The results show that when the MVD value of SLD is large， compared with LEWICE model and Trujillo model， the calculation results of local collection efficiency of airfoil surface and impingement range calculated by combining the two models are more consistent with the test data， and the error of most of the calculation results is less than 10% compared with the test data; the larger the MVD is， the closer the calculation result of the local collection efficiency value is to the test value.

Keywords：supercooled large droplets; numerical simulation; deformation; bounce; splash

0 引言

過冷大水滴（supercooled large droplets， SLD）是指云層中平均容積直徑（median volume diameter，MVD）大于50μm的過冷水滴。飛機和發動機在含有過冷大水滴的環境中飛行時，會發生結冰現象。過冷大水滴在運動和撞擊過程中，會發生變形、破碎、反彈、飛濺等復雜現象，所產生的二次小水滴可能會再次撞擊^[1]。過冷大水滴的這些特性使其撞擊范圍和結冰范圍較大，也容易產生溢流水，并導致在防護區域外形成脊狀冰，產生安全隱患。水滴的運動和撞擊特性是結冰和防冰預測的前提，而常規尺寸水滴運動和撞擊特性的模擬方法通常不需要考慮水滴的破碎、飛濺和反彈等現象，但并不適用于大水滴。因此對過冷大水滴運動和撞擊特性的研究是十分有必要的。

國內外研究學者對此開展了一系列理論、數值和試驗研究。為了描述過冷大水滴運動和撞擊過程中出現的變形、破碎、反彈和飛濺等現象，國外學者結合試驗數據建立了相關的經驗或半經驗模型^[2]。針對過冷大水滴運動過程中發生的變形，1933年LIU等^[3]、1978年CLIFT等^[4]分別提出了兩種過冷大水滴阻力系數的模型。針對過冷大水滴撞擊壁面過程中發生的反彈、飛濺現象，WRIGHT、MACKLIN等^[5-6]提出了相應的計算模型，分別被LEWICE軟件^[7]、FENSAP-ICE軟件^[8]采用，TRUJILLO等^[9]也提出了類似的飛濺模型。2010年，IULIANO等^[10]采用Clift的阻力模型和不同的反彈/飛濺模型計算了SLD在翼型上的撞擊特性。結果表明，采用Trujillo模型預測MVD為111μm的SLD撞擊到NACA23012翼型表面的水收集系數峰值比試驗值低約20%，采用LEWICE模型預測MVD為94μm的SLD撞擊到MS（1）-0317翼型表面的水收集系數峰值高于試驗值約30%。2021年，王龍等^[11]采用水平集法從微觀角度研究水滴撞擊過程，通過數值模擬研究半徑1.3mm的過冷大水滴撞擊特性，發現大水滴運動過程中存在回流。2004年，PAPADAKIS等^[12]在NASA冰風洞中獲得了MVD分別為20μm、52μm、111μm、154μm和236μm的過冷水滴在NACA23012翼型表面的撞擊特性試驗數據。

如上所述，國內外學者計算得到的過冷大水滴撞擊特性結果和試驗數據相比，精度不夠高。為了更準確地模擬過冷大水滴在結冰部件表面的撞擊特性，本文采用考慮過冷大水滴運動過程中變形的Clift模型，結合考慮過冷大水滴撞擊過程中反彈/飛濺的LEWICE模型和Trujillo模型，以NACA23012翼型為研究對象，通過Fluent軟件的二次開發功能，對過冷大水滴的運動和撞擊特性進行數值模擬，并將計算結果與NASA的試驗數據進行對比分析。

1 數學模型和計算方法

1.1 過冷大水滴運動過程中的變形模型

本文采用歐拉法計算水滴流場。根據守恒定律可得水滴的連續方程和動量方程^[13]分別為：

式中：ρ_d為水滴密度；α為水滴的容積分數；u_d為水滴的速度矢量；u_a為空氣的速度矢量；μ_a為空氣的動力黏度；d為將水滴視為規則球體時的水滴直徑；Re為以空氣和水滴之間的相對速度作為特征速度的雷諾數，表達式為

式中ρ_a為空氣密度。大水滴由于尺寸較大，其表面張力不容易克服所受的空氣剪切力，因此在運動過程中會發生變形，水滴形狀會由球狀向類似扁圓盤狀過渡。采用水滴韋伯數表征水滴慣性力和表面張力之間的相對大小，其表達式為

式中σ_d為水滴的表面張力。變形后的水滴受到的空氣阻力發生改變，本文采用Clift提出的變形模型模擬大水滴形狀改變所導致的阻力系數變化。該模型取球體阻力系數C_D，sphere和扁圓盤阻力系數C_D，disk的加權平均值來描述大水滴變形后的阻力系數C_D，其表達式為

式中e為插值系數，表達式為

式（5）中球體阻力系數C_D，sphere為

式（5）中扁圓盤阻力系數C_D，disk為

1.2 過冷大水滴撞擊過程中的反彈/飛濺模型

過冷大水滴在撞擊壁面后，會發生反彈和飛濺，其引起的水滴質量損失較大。反彈是指水滴在撞擊到壁面后以一定角度離開壁面；飛濺是指水滴在撞擊壁面后部分水滴停留在壁面，部分飛離壁面。本文使用LEWICE軟件中SLD反彈/飛濺模型和TRUJILLO的SLD飛濺模型，模擬過冷大水滴撞擊壁面反彈/飛濺現象。

1）LEWICE的模型

LEWICE軟件應用了WRIGHT等提出的同時考慮了水滴的反彈和飛濺質量損失的大水滴撞擊模型。模型中采用了MACKLIN等提出的與R_e，s數和O_h數有關的飛濺參數K，其表達式為

式中O_h數為

R_e，s數的表達式為

式中u_d，n為水滴速度在壁面上的法向分量。定義耦合水滴撞擊能和入射頻率的水滴撞擊參數K_L，作為判斷發生反彈、飛濺現象的衡量參數，其表達式為

式中：θ為水滴速度和撞擊表面切向的夾角；f^*為無量綱水滴頻率，定義為

由于反彈/飛濺效應引起的過冷大水滴撞擊質量損失用無量綱質量損失系數f_m，lewice表示為

2）Trujillo模型

TRUJILLO等提出的大水滴撞擊模型考慮了水滴飛濺引起的質量損失，滿足以下條件時水滴飛濺發生^[14]：

式中：K_Ctr為判斷飛濺發生的臨界參數；R為撞擊表面粗糙度相對水滴直徑的比值，表達式為

式中R_s為撞擊表面的最大粗糙度，其可由試驗結果^[15]確定。該模型的無量綱質量損失系數f_m，trujillo為

1.3 計算方法

本文通過Fluent軟件的二次開發功能，結合上述數學模型，對過冷大水滴的運動和撞擊特性進行數值計算，包含以下3個模塊。

1）空氣流場計算。首先計算部件外空氣流場，由于水滴含量很少，忽略其對空氣的影響，使用Fluent軟件的單相流求解器求解空氣相的連續方程、動量方程以及相應的湍流方程，獲得部件外空氣流場的速度、壓力等分布。

2）過冷水滴流場計算。在上一步計算好的空氣流場基礎上，加載編譯用于求解水滴流場的UDF文件。該UDF文件中將過冷水滴的連續方程和3個坐標方向的動量方程視為4個標量輸運方程，即使用Fluent軟件的用戶自定義標量UDS（user defined scalars）功能定義4個輸運方程（UDS0—UDS3），UDS0—UDS3分別表示水滴容積分數和水滴在x、y、z 3個方向的速度分量，其中水滴動量方程的阻力系數應用Clift的SLD變形模型。以此對一定邊界條件約束下水滴運動的連續方程和動量方程進行離散，迭代求解得到水滴流場的容積分數、水滴速度等的分布。

3）水滴撞擊特性計算。在空氣和過冷水滴兩相流場結果的基礎上，使用Fluent軟件的用戶自定義內存UDM（user defined memories）功能，依次求解得到質量損失系數f_in，lewice和f_m，trujillo，再結合上述兩個SLD撞擊模型求解得到最終的局部水收集系數β。

2 計算模型

2.1 計算域和邊界條件

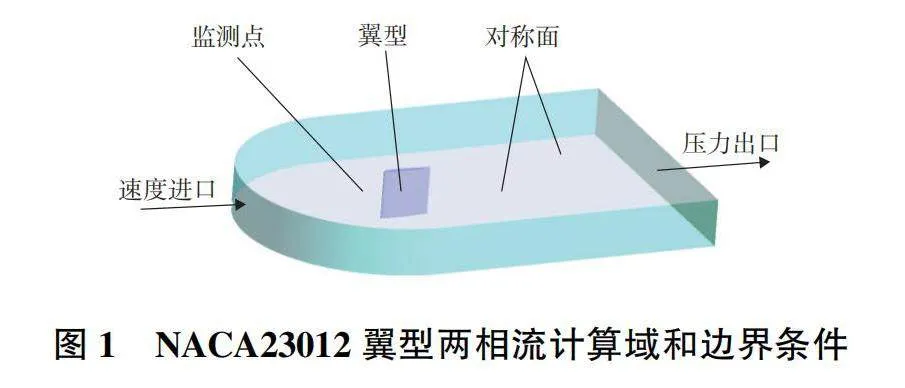
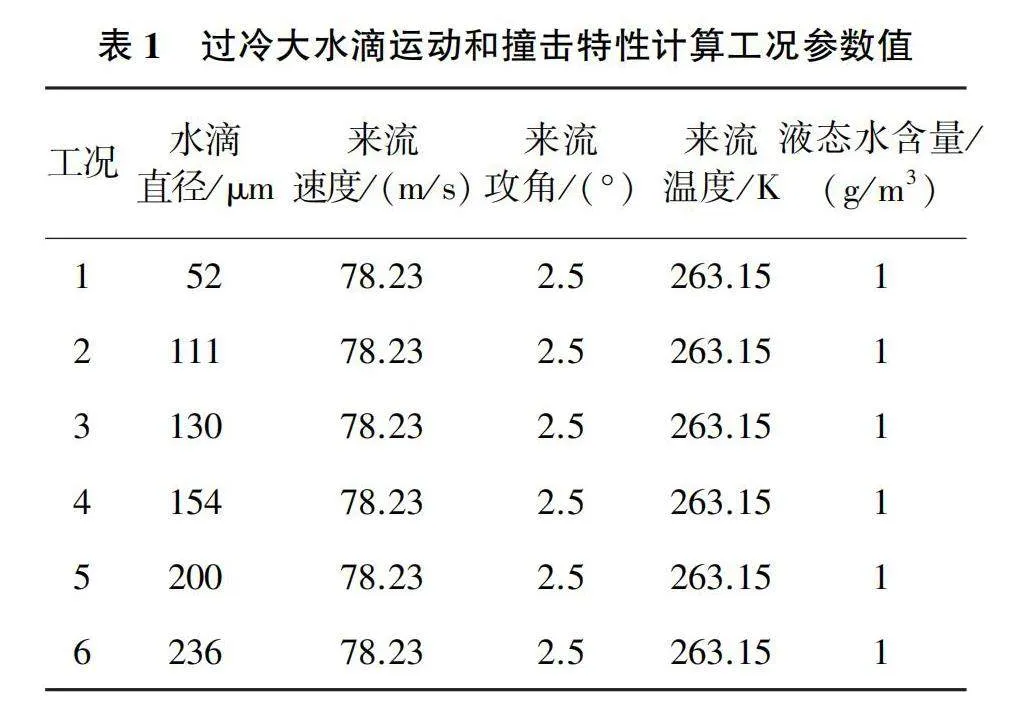
本文以NACA23012翼型為研究對象，其弦長為0.914 4m，展向高度為0.914 4m。建立如圖1所示的翼型外部空氣-過冷大水滴兩相流計算域。該計算域的進口邊界為速度進口，出口邊界為壓力出口，壓力為1個大氣壓。本文在來流速度、溫度和液態水含量均相同的情況下計算不同MVD的過冷大水滴運動和撞擊特性，具體計算邊界條件參數如表1所示。

2.2 網格劃分及獨立性驗證

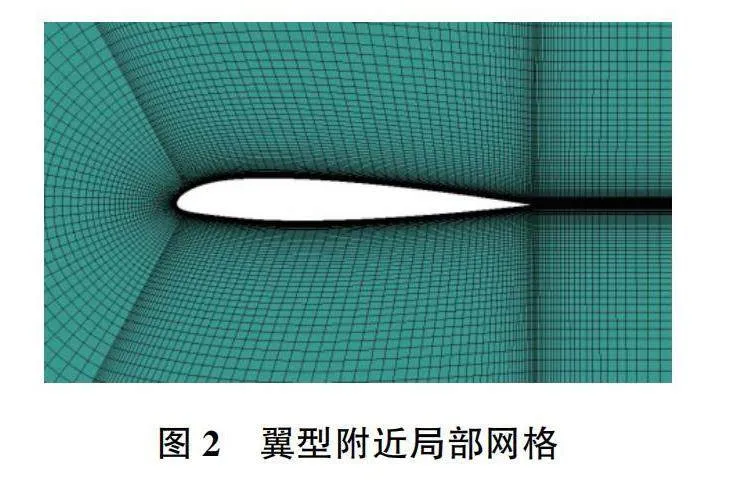
采用ANSYS ICEM商業軟件對計算域進行網格劃分，全域劃分六面體結構化網格，并對翼型壁面網格進行加密處理，如圖2所示。由于空氣流場計算采用k-ε湍流模型并結合Realizable壁面函數，劃分翼型壁面附近第一層網格尺度為0.2mm，對應的y⁺約為30。

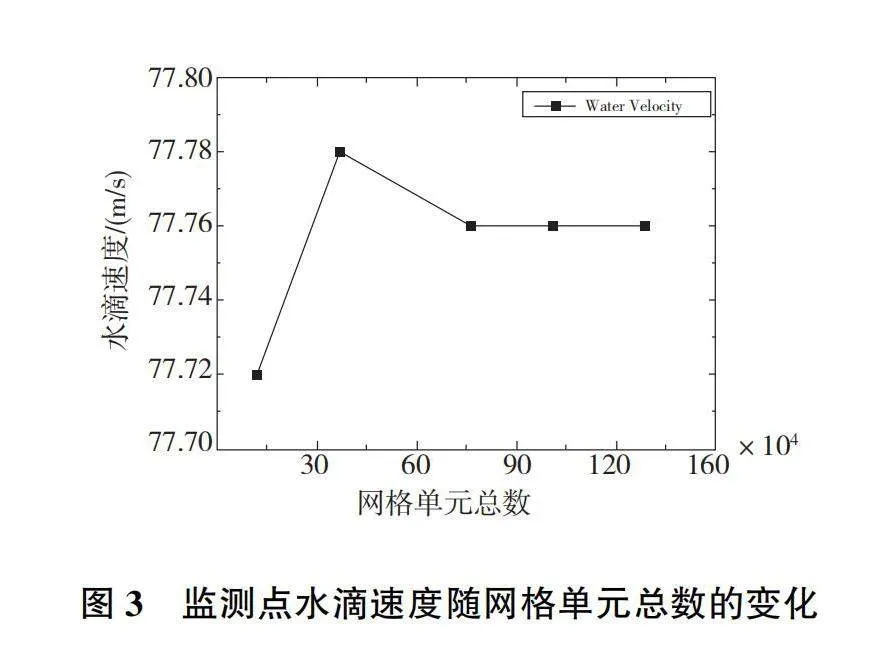
為了消除網格疏密對計算結果的影響，分別采取單元總數分別為12萬、37萬、76萬、101萬和129萬的5套網格進行兩相流場計算，對比不同計算網格下圖2所示的監測點處水滴速度，以此進行網格獨立性驗證。圖3為監測位置處水滴速度隨網格數量變化的結果。由圖3可知，當網格總數大于76萬時，監測點的水滴速度不再隨網格數量變化，因此本文最終選用總數101萬的網格進行計算。

3 計算結果及分析

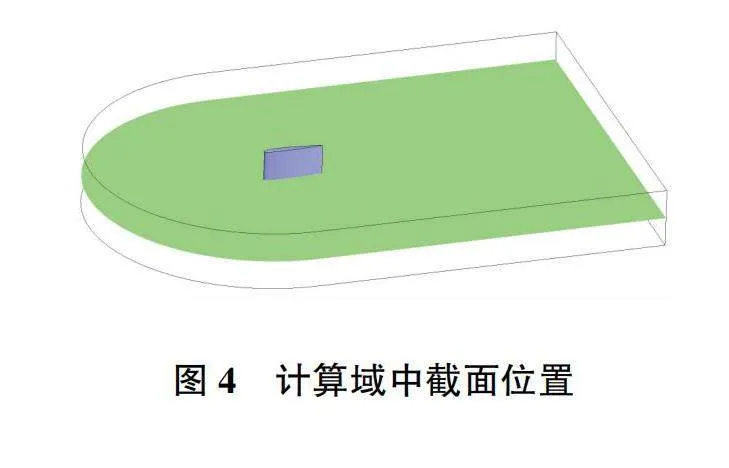
為描述方便，在計算域展向的中部垂直于展向截取一個中截面如圖4所示，因該翼型沿展向的各截面均相同，故分析該中截面上的流場計算結果即可。

3.1 運動特性分析

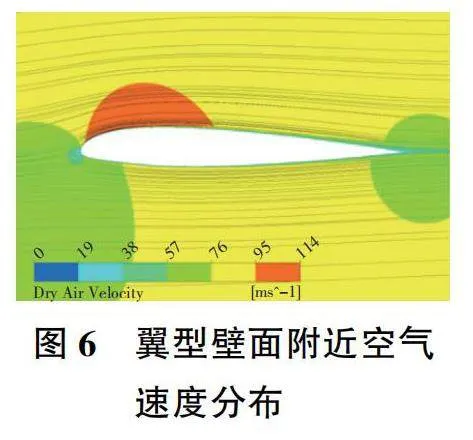
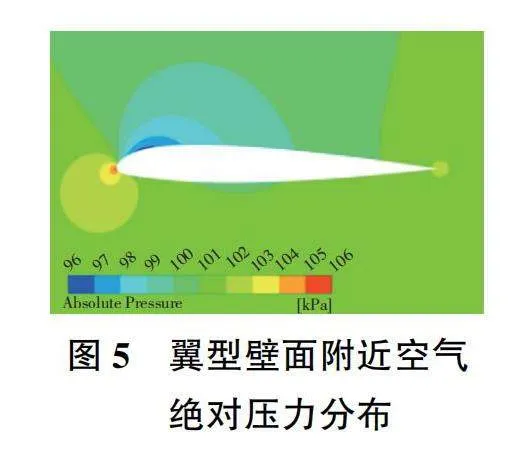
根據本文的計算方法，計算空氣流場時忽略過冷水滴的影響，故6個算例的空氣流場計算結果相同。計算域中截面上的絕對壓力分布和空氣速度分布分別如圖5和圖6所示。由圖可知，翼型駐點處的壓力最大，約為106kPa，沿著翼型上下表面，壓力先降低后上升，但并不對稱，且在相同的流向坐標處，上表面的壓力較小。

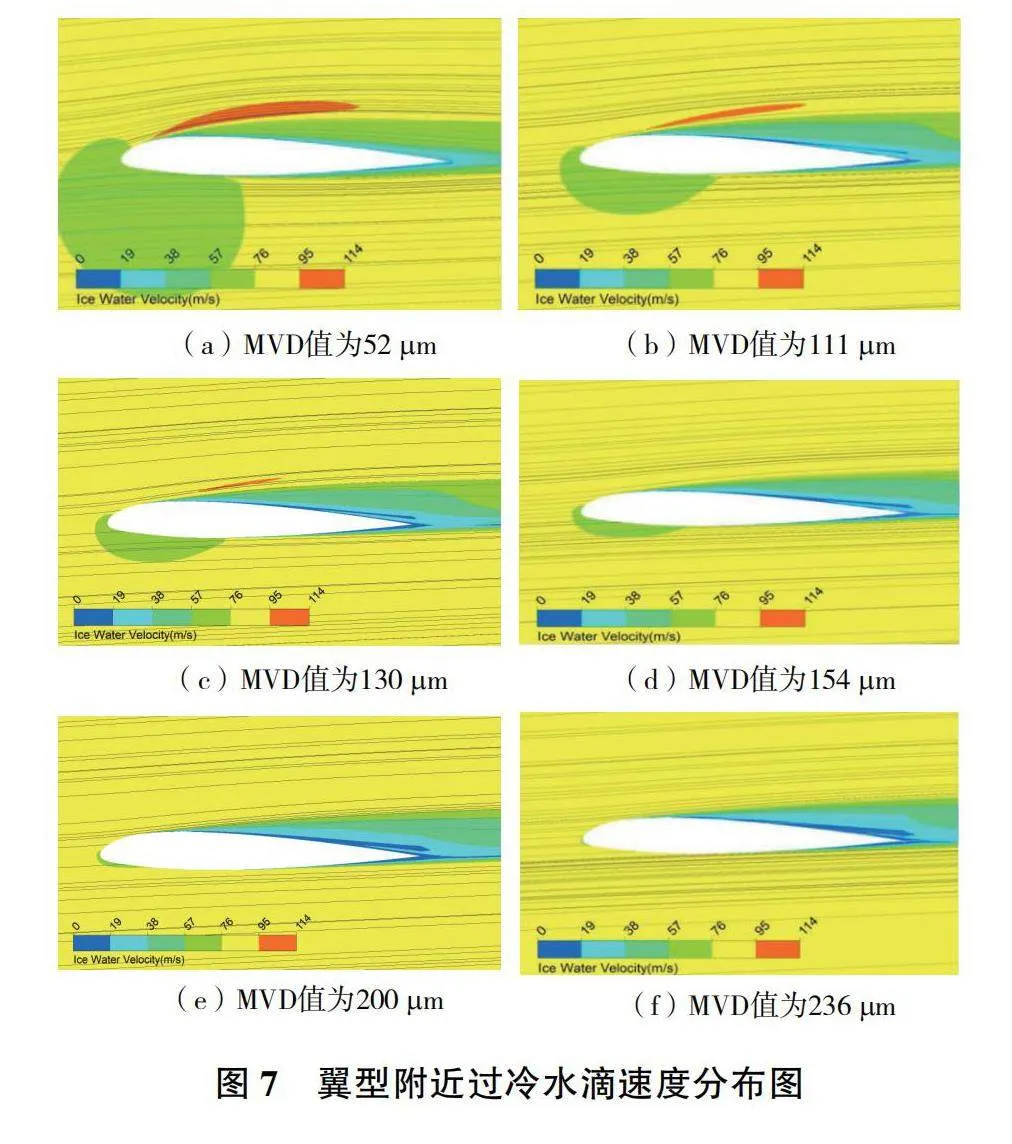
雖然6個算例的空氣流場完全一致，但加入過冷大水滴后，因水滴的直徑不同，則空氣對水滴的氣動力不同，導致水滴的速度分布和容積分數分布不同。6個算例中截面上的水滴速度分布如圖7所示（本刊黑白印刷，相關疑問咨詢作者）。

圖7（a）所示為MVD值為52μm時的水滴速度分布，駐點附近速度較低，沿流向往下游，速度先上升后下降，但相同位置處水滴速度值略小于空氣速度值。與空氣速度分布相比不同之處在于，翼型上部水滴速度值較大的紅色區域呈扁長狀，沿流向延伸至翼型的中后部。由圖7（a）—圖7（f）可見，隨著MVD值增大，翼型外部水滴速度值較高的紅色區域減小，為水滴的最大速度值也降低。這是因為隨著過冷大水滴尺寸增大，水滴慣性增大，更不容易被空氣帶動，其流動方向趨向于直線。

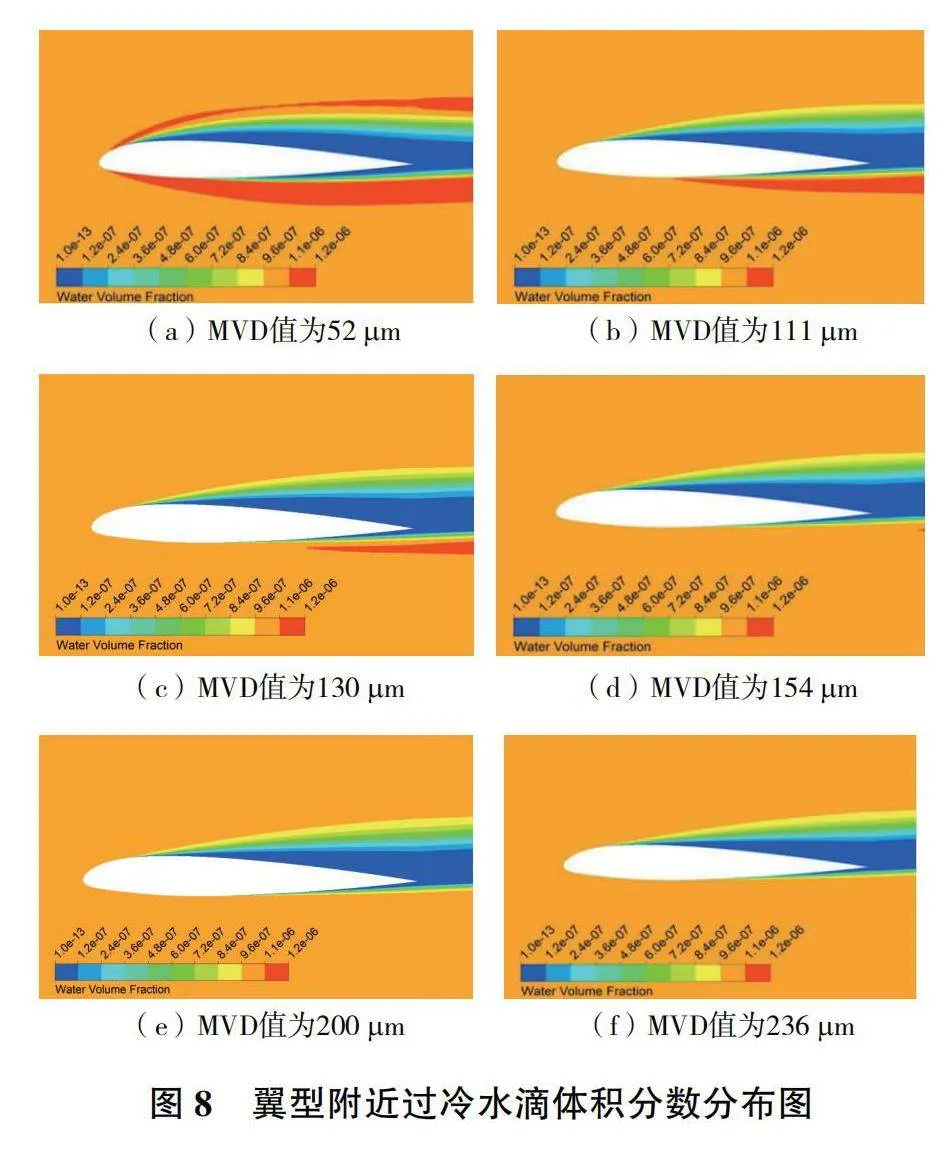
不同MVD值下翼型附近水滴體積分數分布如圖8所示。由圖8（a）可見，MVD值為52μm時，在稍遠離翼型的流場區域，水滴體積分數值與進口處基本相同。在緊貼翼型壁面處，沿著流向從駐點向下游，水滴的體積分數減小。越靠近翼型壁面，水滴的體積分數值越小，直至體積分數為0的遮蔽區。對比圖8（a）—圖8（f）可見，隨著MVD值增大，水滴體積分數大的紅色區域減小，這是因為隨著水滴直徑增大，水滴慣性增大，更多的水滴撞擊到翼型壁面并被收集。由于翼型前部的遮擋，導致翼型中后部附近過冷水滴無法到達，形成體積分數幾乎為0的遮蔽區。

3.2 過冷大水滴撞擊特性分析

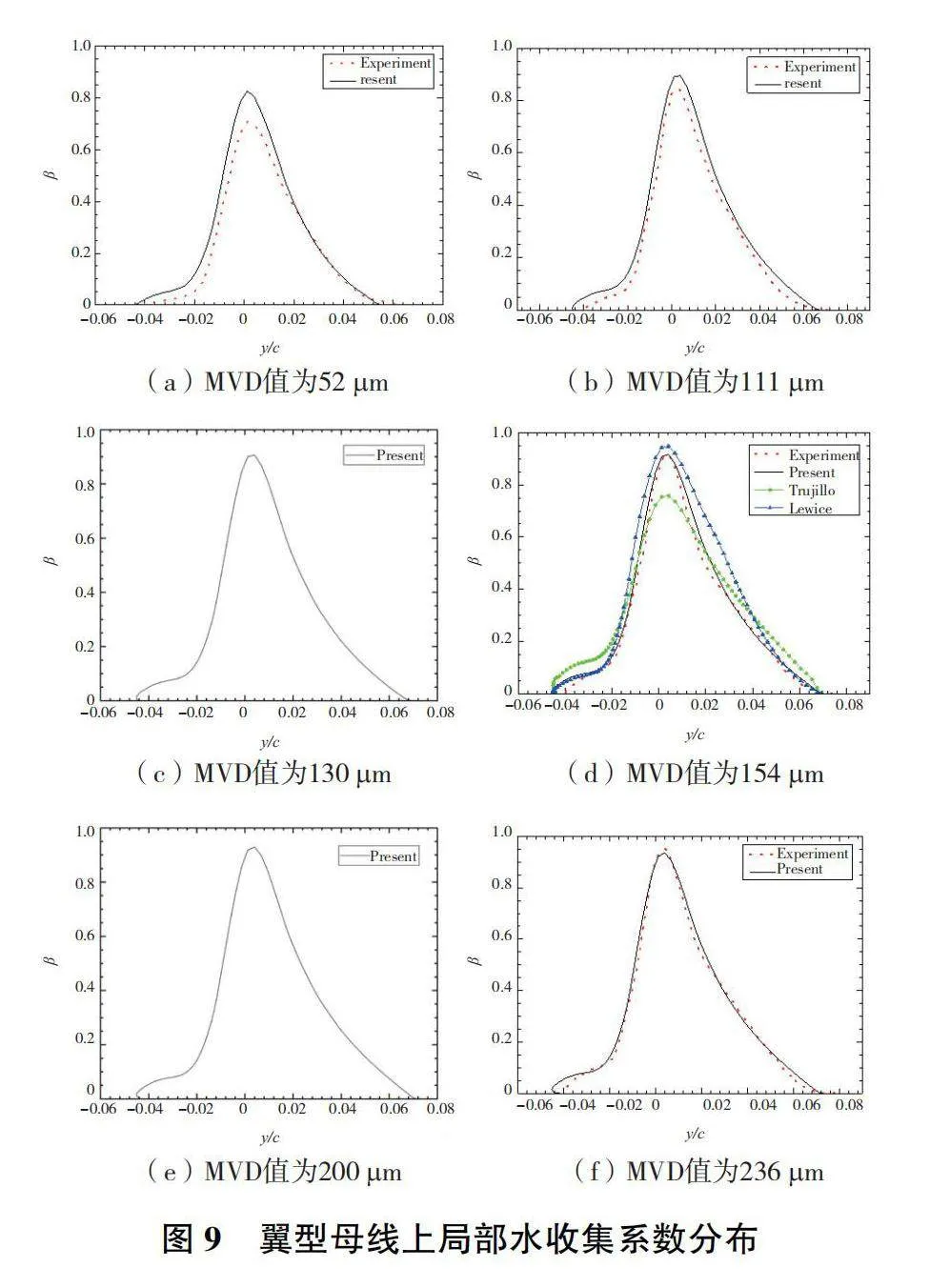
取計算域中截面與翼型壁面相交的輪廓線上的局部水收集系數，并與Papadakis的試驗數據進行對比，如圖9所示。圖中橫坐標y/c表示翼型表面從駐點處開始的弧長坐標y與弦長c之比，y/cgt;0為翼型上表面，y/clt;0為翼型下表面。由圖9可知，水滴撞擊集中在翼型前緣，翼型駐點處局部水收集系數最大，從駐點向后，局部水收集系數降低，在翼型前緣下游，局部水收集系數迅速降低為0。從圖9（a）—圖9（f）可以看出，隨著MVD值增大，水滴的撞擊范圍略微增大。這也是由于水滴直徑增大使得其慣性增大所致。

由圖9（a）可見，MVD值為52μm時，翼型下表面和駐點附近水收集系數的計算值比試驗數據略高，兩者存在少許偏差，其中駐點處相差約0.1。從駐點附近往下游，翼型上表面水收集系數計算值和試驗值的重合度高。由圖9（b）—圖9（f）可知，本文的計算結果與試驗數據總體符合較好，在翼型表面的絕大部分范圍內，計算值和試驗值之間的差值均低于10%。

4 結語

為了更準確地模擬過冷大水滴在結冰部件表面的撞擊特性，以NACA23012翼型為研究對象，通過Fluent軟件的二次開發功能，采用Clift過冷大水滴變形模型，并基于LEWICE模型和Trujillo模型的兩個過冷大水滴反彈、飛濺模型，對過冷大水滴的運動和撞擊特性進行了數值模擬。計算得到了流場的空氣速度、壓力分布，水滴的速度、體積分數分布以及翼型表面局部水收集系數分布，并將局部水收集系數分布結果與試驗數據進行對比，驗證了本文計算模型和計算方法的合理性。本文主要研究結論如下。

1）空氣-過冷大水滴兩相流在翼型駐點附近速度較低，沿流向往下游，速度先上升后下降。相同位置處，過冷水滴速度值略低于空氣速度值。翼型上部水滴速度值較大的紅色區域呈扁長狀，沿流向延伸至翼型的中后部。

2）其他條件相同的情況下，隨MVD值增大，翼型外部過冷水滴高速度值區域范圍減小，水滴速度最大值降低，水滴流線越來越趨近于直線。

3）翼型附近外水滴體積分數沿流向從駐點向下游逐漸減小，越靠近翼型壁面，水滴的體積分數值越小，直至為0。隨MVD值增大，水滴體積分數較高的區域減小。

4）過冷大水滴撞擊集中在翼型前緣，翼型駐點附近局部水收集系數最大，從駐點向后，局部水收集系數降低，在翼型前緣下游局部水收集系數迅速降低為0。

5）當過冷大水滴的MVD值較大時，與LEWICE模型和Trujillo模型相比，結合兩個模型計算所得的翼型表面局部水收集系數計算結果和撞擊范圍與試驗數據符合較好，MVD值越大，計算值與試驗值越吻合，由此驗證了采用本文的計算模型和計算方法在計算過冷大水滴運動與撞擊特性時具有適用性和有效性。

參考文獻：

[1] 林貴平，卜雪琴，申曉斌. 飛機結冰與防冰技術[M]. 北京：北京航空航天大學出版社，2016.

[2] WRIGHT W，POTAPCZUK M. Semi-empirical modelling of SLD physics[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada. Reston，Virginia：AIAA，2004：412.

[3] LIU A B，MATHER D，REITZ R D. Modeling the effects of drop drag and breakup on fuel sprays[C]//SAE Technical Paper Series. 400 Commonwealth Drive，Warrendale，PA，United States：SAE International，1993：930072.

[4] CLIFT R，GRACE J R，WEBER M E. Bubbles，drops，and particles[M]. New York：Academic Press，1978.

[5] WRIGHT W，POTAPCZUK M，LEVINSON L. Comparison of LEWICE and GlennICE in the SLD regime[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada. Reston，Virginia：AIAA，2008：439.

[6] MACKLIN W C，METAXAS G J. Splashing of drops on liquid layers[J]. Journal of Applied Physics，1976，47（9）：3963-3970.

[7] WRIGHT W. User’s Manual for LEWICE Version 3.2[M]. [S.I.]：Nasal/Cr， 2008.

[8] HONSEK R，HABASHI W G. FENSAP-ICE：Eulerian modeling of droplet impingement in the SLD regime of aircraft icing[C]//44th AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada. Reston，Virginia：AIAA，2006：465.

[9] TRUJILLO M F，MATHEWS W S，LEE C F，et al. Modelling and experiment of impingement and atomization of a liquid spray on a wall[J]. International Journal of Engine Research，2000，1（1）：87-105.

[10] IULIANO E，MINGIONE G，PETROSINO F，et al. Eulerian modeling of SLD physics towards more realistic aircraft icing simulation[C]//AIAA Atmospheric and Space Environments Conference. Toronto，Ontario，Canada. Reston，Virginia：AIAA，2010：7676.

[11] 王龍，汪寧，來永斌，等. 大水滴撞擊翼型后的破碎過程研究[J]. 應用力學學報，2021，38（3）：1071-1078.

[12] PAPADAKIS M，RACHMAN A，WONG S C，et al. Water impingement experiments on a NACA 23012 airfoil with simulated glaze ice shapes[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno，Nevada. Reston，Virginia：AIAA，2004：565.

[13] BOURGAULT Y，HABASHI W，DOMPIERRE J，et al. An Eulerian approach to supercooled droplets impingement calculations[C]//35th Aerospace Sciences Meeting and Exhibit. Reno，NV. Reston，Virginia：AIAA，1997：176.

[14] YARIN A L，WEISS D A. Impact of drops on solid surfaces：self-similar capillary waves，and splashing as a new type of kinematic discontinuity[J]. Journal of Fluid Mechanics，1995，283：141-173.

[15] ANDERSON D，HENTSCHEL D，RUFF G. Measurement and correlation of ice accretion roughness[C]//36th AIAA Aerospace Sciences Meeting and Exhibit. Reno，NV. Reston，Virginia：AIAA，1998：486.

收稿日期：2023-01-30