反比例函數的奇妙世界

反比例函數，用簡潔而優美的形式表達著兩個變量之間的反比例關系。它告訴我們，在某些情況下，當一個量增加時，另一個量則會相應地減少，兩者之間存在一種微妙的平衡。它的圖像，是一條雙曲線，無限延伸卻永不相交，展現了數學的對稱之美，也讓我們感受到了規律的嚴謹與奇妙。

今天我給大家分享一下反比例函數的三條常用性質和六個模型，簡稱“三頭六臂”。

“三頭”包括反比例函數的不變性，即一“乘”不變，xy=k，|k|越大，函數圖像離原點越遠；增減性，即同一象限用增減，不同象限看符號；對稱性，即關于原點中心對稱，關于直線y=±x對稱。

“六臂”，即有6種模型，具體如下：

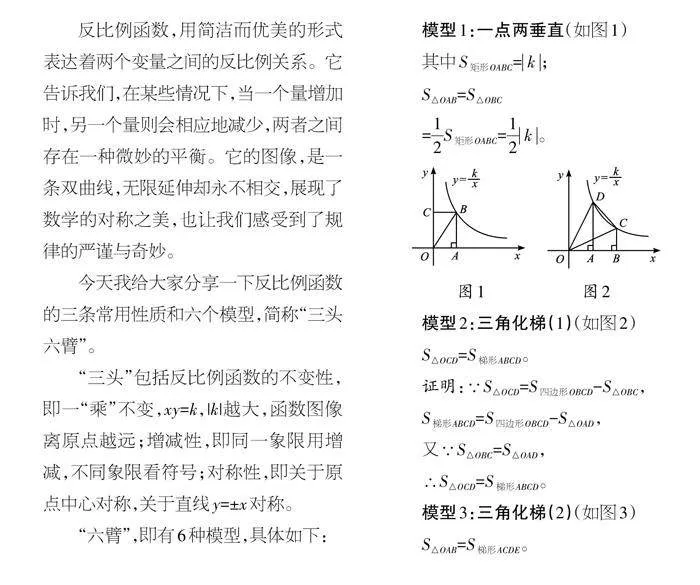
模型1：一點兩垂直（如圖1）

其中S矩形OABC=[k]；

S△OAB=S△OBC

=[12]S矩形OABC=[12][k]。

模型2：三角化梯（1）（如圖2）

S△OCD=S梯形ABCD。

證明：∵S△OCD=S四邊形OBCD-S△OBC，

S梯形ABCD=S四邊形OBCD-S△OAD，

又∵S△OBC=S△OAD，

∴S△OCD=S梯形ABCD。

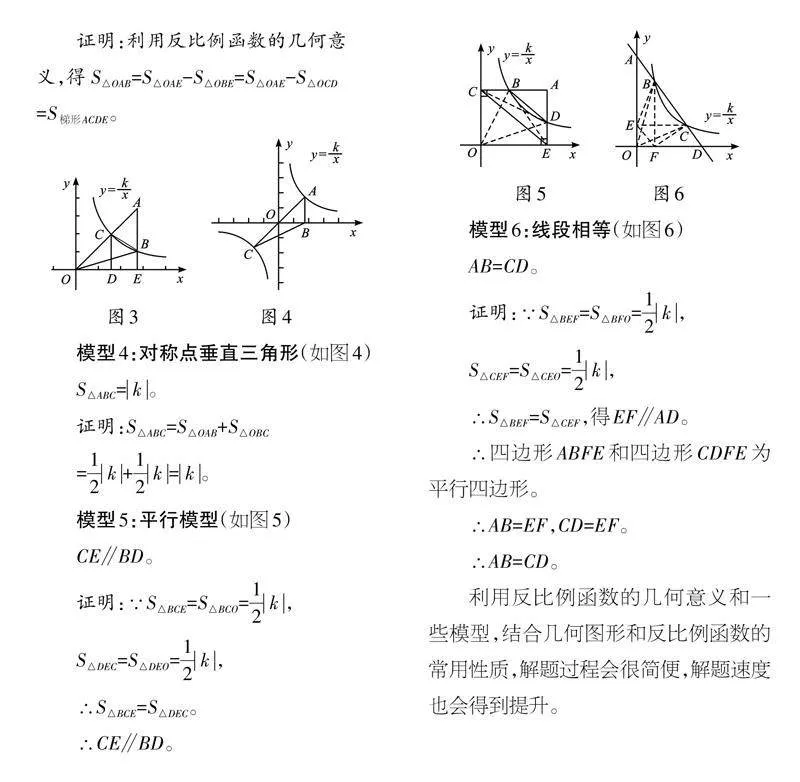
模型3：三角化梯（2）（如圖3）

S△OAB=S梯形ACDE。

證明：利用反比例函數的幾何意

義，得S△OAB=S△OAE-S△OBE=S△OAE-S△OCD

=S梯形ACDE。

模型4：對稱點垂直三角形（如圖4）

S△ABC=[k]。

證明：S△ABC=S△OAB+S△OBC

=[12][k]+[12][k]=[k]。

模型5：平行模型（如圖5）

CE∥BD。

證明：∵S△BCE=S△BCO=[12][k]，

S△DEC=S△DEO=[12][k]，

∴S△BCE=S△DEC。

∴CE∥BD。

模型6：線段相等（如圖6）

AB=CD。

證明：∵S△BEF=S△BFO=[12][k]，

S△CEF=S△CEO=[12][k]，

∴S△BEF=S△CEF，得EF∥AD。

∴四邊形ABFE和四邊形CDFE為平行四邊形。

∴AB=EF，CD=EF。

∴AB=CD。

利用反比例函數的幾何意義和一些模型，結合幾何圖形和反比例函數的常用性質，解題過程會很簡便，解題速度也會得到提升。

教師點評

王瑞琦同學在解決反比例函數問題后總結了三條常用性質和六個模型。模型是對某類題系統地簡化和概括得到的，可見該同學在學習過程中滲透了模型思想。總結模型是對解題的進一步深化，是透過現象看到本質的過程。

（指導教師：崔建平）