GeoGebra軟件在可視化教學中的應用研究

［摘 要］ 將信息技術合理應用于數學教學領域是時代發展的必然趨勢，它可滿足可視化教學的需求. 文章從GeoGebra軟件、可視化教學、GeoGebra與可視化三個核心主題的界定出發，探討GeoGebra軟件在可視化教學中的應用需遵循信息組塊避免冗余效應、多元聯系踐行深度學習、動態探索激發高階思維三個原則，并從概念生成、命題發現、問題解決三個方面具體談一談GeoGebra軟件在可視化教學中的實踐.

［關鍵詞］ GeoGebra軟件；可視化教學；實施原則

隨著信息技術在教育領域的普及，當代數學教學模式與傳統數學教學模式相比，發生了翻天覆地的改變，信息技術已廣泛應用到課堂教學中. 在學生認知負荷較重的背景下，教師需綜合考慮教學內容與教學技術等因素，選擇行之有效的教學方式提升教學效率. GeoGebra軟件具有代數運算、幾何作圖與數據處理等作用，為可視化數學教學帶來了更多便利.

核心主題界定

1. GeoGebra軟件

GeoGebra是一個結合代數、幾何、微積分的動態數學軟件. 教師可在該軟件上直接畫點、線段、直線、向量、曲線、多邊形或函數圖象等，也可通過輸入方程和點坐標獲得相應圖象. GeoGebra軟件界面有幾何窗口與代數窗口，兩者具有對應關系，如改變代數數據，幾何圖象隨之發生改變，反之亦然. 因此，這是一種具備同時處理幾何圖形與代數數據功能的軟件.

2. 可視化教學

1987年美國自然科學基金會提出“可視化（Visualization）”一詞，指借助一定的手段處理數據，使之形成可視化的圖形或圖象展示出來. 可視化教學是指教師借助信息技術手段，如GeoGebra或幾何畫板等軟件的演示功能，將學生難以理解的知識轉化成具體的圖形或動畫，使學生能更好地接受抽象的知識. 這種教學手段省略了很多煩瑣冗長的教學過程，有效提高了課堂教學效率.

3. GeoGebra與可視化

俗話說“一圖勝千文”. 數學可視化教學可將抽象的數學知識直觀地展示在學生面前，幫助學生更好地發現、理解與建構數學知識. GeoGebra軟件的介入，使代數方程或坐標與圖形同步變化，學生對數學知識的理解更加直觀，從真正意義上實現了“數與形”的有機結合. 同時，在GeoGebra軟件中輸入代數指令可為學生呈現動態的圖形演示過程，讓學生能更好地洞察數學世界，感知數學的獨特魅力.

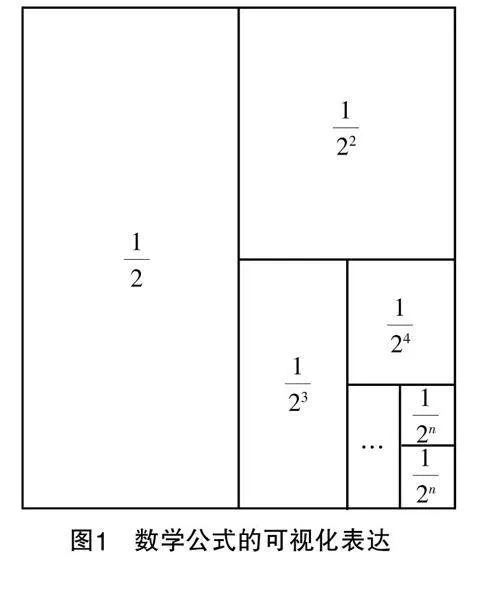
例如，對于式子++…++=1-的證明，從代數的角度應用等比數列求和法或錯位相減法固然可以求證，但若借助GeoGebra軟件，通過圖形展示（見圖1）進行“無字證明”，可讓學生從可視化的圖形中對該式一目了然，帶給學生耳目一新之感.

由此可見，GeoGebra軟件是實現可視化教學的重要工具之一，而可視化又是展示GeoGebra軟件優勢的重要方式，將兩者有機地融合在一起對提高數學課堂教學效率具有重要意義.

實施原則

1. 信息組塊避免冗余效應

視覺表征以可視化為載體，課堂借助動畫影像、圖象等直觀形式，向學生展示抽象的數學知識，引導學生感知教學內容的豐富和直觀，使學生更容易在內心建構形象化的數學信息，為實際應用奠定基礎. 因此，視覺表征屬于一種富有表現力的展示形式，學生從中能接收到豐富的信息. 值得注意的是，“讀圖”雖能有效提高學生對問題的理解程度，但過于復雜的圖象會帶來負面效應，讓學生感到視覺疲勞.

究竟該如何降低學生的認知負荷，借助GeoGebra軟件提高課堂可視化的教學成效呢？一方面需要關注可視化的效果，如利用曲線的動靜結合、構圖元素的疏密錯落、豐富的色彩等提升學生的視覺感受；另一方面借助GeoGebra軟件對可視化內容進行信息組塊，借助多元方式調配組合相應的教學內容，提高學生的理解能力.

2. 多元聯系踐行深度學習

基于數學知識來看，學生在課堂中所接觸到的新知相對而言都比較抽象，執意用一種方法描述新知，不同認知水平的學生接受時難免出現偏差，而且單一的描述形式也不能揭露知識本質. 事實上，課堂上單一或不恰當的表達方式也是導致學生出現思維卡殼的關鍵因素. 為了突破這一障礙，最好的辦法就是在課堂上應用豐富的圖文等多種形式表達知識內涵，如此不僅能深化學生對知識的理解，還能幫助學生構建完善的知識結構，不斷優化學生的解題策略. 然而，表征系統間的轉譯并非一件容易的事情，若想充分發揮好多元表征在教學中的優勢，可利用各種表征間有意義的聯系進行，以便系統內化外在的數學符號.

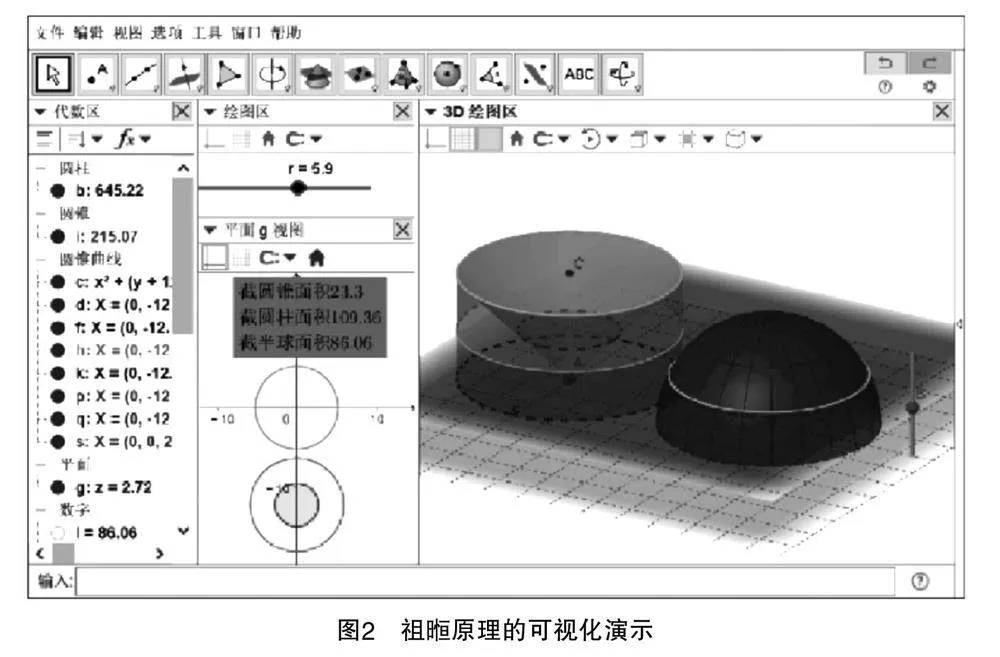
如圖2所示，此為祖暅原理的可視化呈現，即用3D繪圖區的立體圖形展示祖暅原理，讓學生從平面的視圖中感知數值情況，體會兩者間的聯系，從真正意義上理解“冪勢既同，則積不容異”的內涵，實現深度學習.

3. 動態探索激發高階思維

多變的幾何位置關系，以及代數內容的豐富性導致數形關系復雜化，構建動態聯系的視覺化情境，不僅能讓學生在知識的動態變化中發現數學規律，還能感知知識的內涵與外延，為靈活應用做鋪墊. 事實上，數學表征的動態聯系，可將表征信息元素與整體關系精細地展示出來，還能將信息元素的結構關系與交互性暴露出來，促使學生對此產生關注，實現表征系統的互相轉譯，發展思維的縝密性與跳躍性，這也是高階思維的形成基礎［1］.

研究發現，動態探索需建立在數形結合上，學生通過對數學模型的探索與構建，自主發現解題思路與策略，從圖形與數量之間的關系中抽象出數學知識的一般結構與規律，從而在問題解決過程中有效提升數學高階思維與核心素養.

實施途徑

1. 應用在概念生成過程中

概念是數學的基礎，是數學思維構成的基石，關注核心概念的教學是發展學生數學思維的重要途徑. 每一個數學概念的表達可以有多重方式，各種表征方式可促使學生產生不一樣的數學思維. 實踐證明，多元表征數學概念有助于學生多角度理解，深化掌握. 將GeoGebra平臺靈活應用在概念生成的過程中，不僅與新課標所倡導的“關注過程性教學”理念相契合，還讓學生能明確認知概念的形成與發展. 多角度表征概念，能增強學生對概念聯系性的理解，在無形中助力學生靈活應用概念來分析與解決一些復雜的數學問題.

案例1 “任意角的三角函數”的教學.

學生在探索任意角的三角函數之前就已經有了一定的認知基礎，新知的建構需基于原有認知體系進行. 因此，在課堂的導入階段可帶領學生回顧舊知，為建構新概念做鋪墊. 新舊知識銜接的過程就是在知識的生長點處引導學生思考的過程. 值得注意的是，新知的建構需突破原有認知體系引發的思維定式，同時對角的終邊上的任意點的聯系產生明確認識.

如圖3所示，借助GeoGebra軟件引導學生基于可視化情境，對銳角三角函數與任意角三角函數的特征產生清晰認識，并從角的動態變化中幫助學生理清如何應用點坐標來定義三角函數，讓學生在坐標度量的結論下認同“用點定義卻與點的位置無關”的觀念，令表征三角函數線的刻畫變得更加合乎情理.

本例提示數學概念的形成與建構，學生的思維需要經歷“由直觀到抽象、由抽象到應用”的變化過程，有時還需要經過循環反復才能實現. 借助GeoGebra軟件對概念進行可視化演示，可讓概念獲得“原型”支持.

2. 應用在命題發現過程中

數學命題是對數學對象關系或性質關系的判斷句，其語言結構為“條件—結論”，屬于一種以邏輯形式刻畫數學對象的基本方法. 若將數學命題安排在其發生與發展的大背景下，不僅可以幫助學生理解知識的來龍去脈，還能讓學生對數學思想變遷的原委產生深刻理解，從真正意義上實現“知其然且知其所以然”.

數學命題的教學就是將命題的邏輯意義轉化成個體心理意義，概念學習與符號表征是數學命題的前提. “析理以辭，解體用圖”均需意象與語言的雙重編碼來編制網絡，構成結構圖式，學生從整體的角度有序檢索信息，實現對命題理解的融會貫通，此為命題關聯性特征的基本體現.

案例2 解題認知圖式的構建.

問題：已知橢圓C：+=1（a>b>0）的焦點和短軸的一個端點恰巧構成一個直角三角形，橢圓C與直線l：y=-x+3有且僅有一個公共點T.

（1）求橢圓C的方程，并寫出點T的坐標；

（2）若坐標原點為點O，直線l′與OT平行，并與橢圓C分別相交于點A，B，與直線l相交于點P，證明存在常數λ可讓AP2=λAP·BP，并求λ的值.

本題為一道綜合題，學生初次接觸難以入手. 教師借助GeoGebra軟件將問題中的動態變化直觀地暴露在學生面前，用仿射變換揭露圓的幾何性質在圓錐曲線中的推廣，通過問題源與流的探索，構建新的命題網（見圖4）：①橫向的類比推理與縱向的歸納思考，其中類比推理主要是從圓的切割線定理出發，分析圓錐曲線中的定制規律；歸納思考則從橢圓切割線定理和相交弦定理發現定值背后的冪定理，經過整合，歸納出圓錐曲線冪定理；②強、弱抽象，強抽象是指從冪定理到切割線定理的探索，弱抽象是將拋物線冪與橢圓冪中的定向參照弱化為圓錐曲線冪.

此類應用屬于難度系數較高的數學探索，如果離開信息技術的輔助，學生很難通過獨立思考揭露解題核心，而有圖有真相的技術參與，則顯著弱化了問題難度，將問題發生、發展的過程完全暴露出來，促使學生自主構建完整的認知圖式.

3. 應用在問題解決過程中

學生對知識的理解程度或學習能力的高低均體現在解題過程中，解題還能錘煉學生的思維，發展學生的綜合素養. 想要幫助學生更好地掌握問題的數形結構，借助GeoGebra軟件研究問題的已知條件與結論之間的因果邏輯關系，探尋層次分明、邏輯清晰、規范表達的支持策略尤為重要.

案例3 問題情境圖的構建.

問題：已知△ABC中的AB=6，AC=8，若△ABC的外心為O，則·的值是多少？

如圖5所示，借助GeoGebra軟件拖動點B，以改變三角形的形狀，從數值表征中發現數量積的不變性特點，因而從一般退化至特殊，即為直角三角形時，點O位于BC上，獲得結論；若從特殊到一般進行逆向分析，可通過向量分解（=+），實現解題.

該過程在可視性支架的輔助下，實現了“特殊與一般”的雙向轉化，隨著實驗數據的輸入，學生的思維也豁然開朗. 因此，將GeoGebra軟件應用在問題解決過程中，可進一步優化解題思路，發展學生的高階思維.

總之，可視化教學的開展，使得學生有更多機會經歷從具體到抽象的數學演變過程，尤其是GeoGebra軟件的應用，既能讓學生看見問題背后的數據，又能讓學生看透問題所蘊含的內容，這是發展學生“三會”能力的基礎，也是發展學生數學學科核心素養的重要途徑.

參考文獻：

張志勇. 高中數學可視化教學：原則、途徑與策略——基于GeoGebra平臺［J］. 數學通報，2018（07）.