基于直觀想象的深度解題探究

摘 要：文章通過對一道三棱錐的外接球問題進行多維度、多角度探析，還原數學本質，精選教學素材的同時，實現一題多解到多題一解的能力轉變，從而培養學生解題思維、提升直觀想象力。

關鍵詞：三棱錐的外接球；直觀想象；深度解題

中圖分類號：G633.6 文獻標識碼：A 文章編號：1673-8918（2024）28-0073-04

《普通高中數學課程標準（2017年版）》指出：直觀想象是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的過程，主要包括：借助空間認識事物的位置關系、形態變化與運動規律；利用圖形描述、分析數學問題；建立數與形的聯系，構建數學問題直觀模型，探索解決問題的思路。在立體幾何的日常教學中，教師通過引導學生多畫圖、多觀察幾類特殊幾何體的特征，讓學生研究幾何體的幾何特征并展開聯想，通過旋轉、補形等方式深度感悟，提升直觀想象力。

一、 試題呈現

在一次聯考中，有這樣一道試題：

在三棱錐A-BCD中，AB=CD=4，CA=BD=2，BC=23，二面角A-BC-D的平面角為60°，則它的外接球的表面積為 。

經考后分析，此題得分率不高，究其原因是本題沒有給出圖形，學生自己畫出來的圖形不準確，缺乏直觀想象，很難找出外接球的球心。

二、 解法探究

思路1：大多數學生選擇用建系的方法，通過設點的方式，把球心坐標計算出來，但計算量很大、費時費力。

解法1：以B為坐標原點，建立如圖1所示的空間直角坐標系，

則C（23，0，0），D（0，2，0），設A為（a，b，c），

由題意知，AC⊥BC，BC⊥BD，

故CA與BD的夾角等于二面角A-BC-D的平面角，

則cos60°=CA·BD｜CA｜·｜BD｜，得12=2b2·2，

由｜BA｜2=a2+b2+c2=16｜CA｜2=（a-23）2+b2+c2=4，解得a=23，b=1，c=3，點A為（23，1，3），

設球心O為（x，y，z），則R2=｜OB｜2=｜OA｜2=｜OC｜2=｜OD｜2得，

R2=x2+y2+z2=（x-23）2+（y-1）2+（z-3）2=（x-23）2+y2+z2=x2+（y-2）2+z2

解得，x=3，y=1，c=33，則R2=｜OB｜2=133，故外接球表面積為4πR2=52π3。

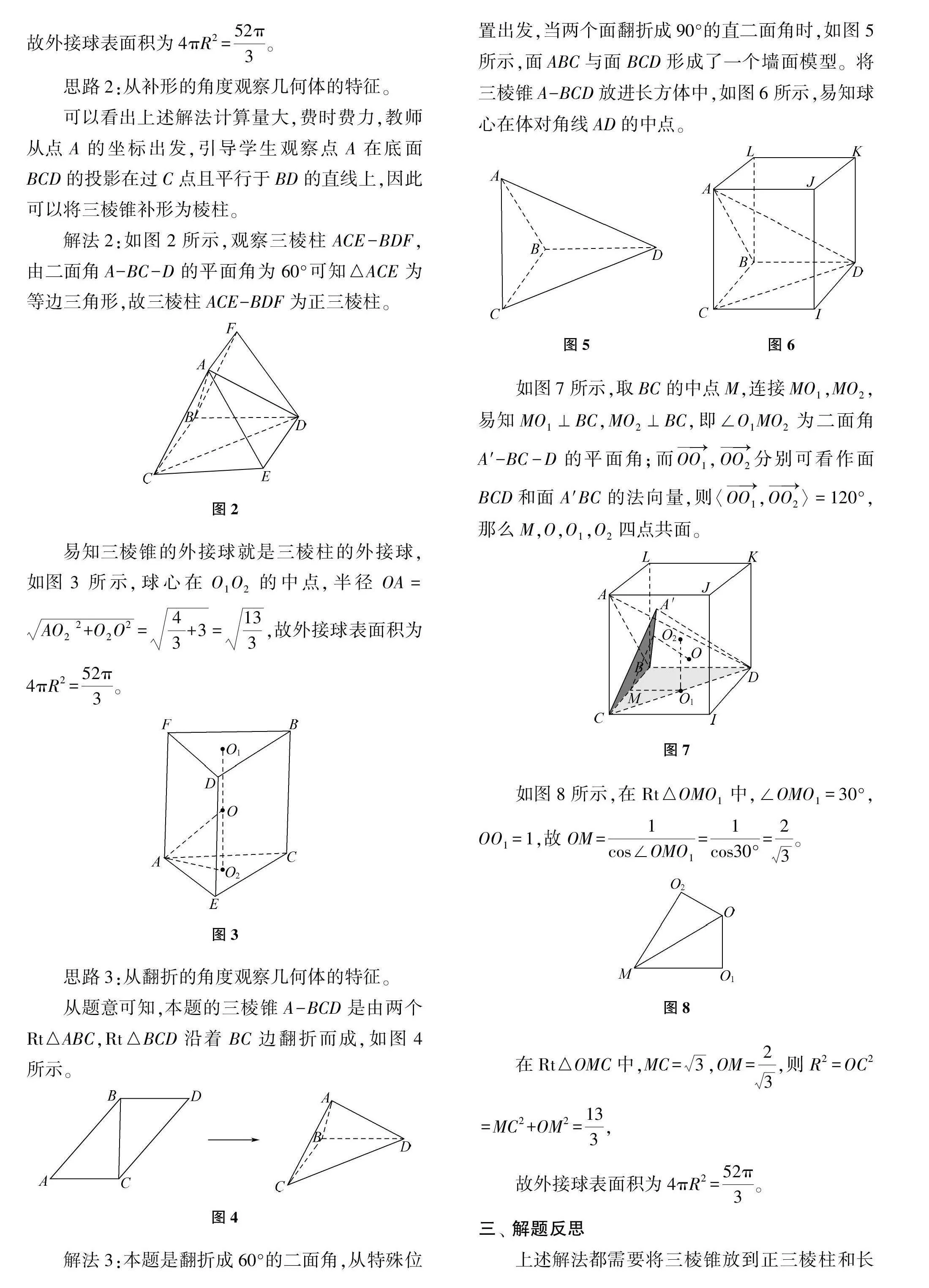
思路2：從補形的角度觀察幾何體的特征。

可以看出上述解法計算量大，費時費力，教師從點A的坐標出發，引導學生觀察點A在底面BCD的投影在過C點且平行于BD的直線上，因此可以將三棱錐補形為棱柱。

解法2：如圖2所示，觀察三棱柱ACE-BDF，由二面角A-BC-D的平面角為60°可知△ACE為等邊三角形，故三棱柱ACE-BDF為正三棱柱。

易知三棱錐的外接球就是三棱柱的外接球，如圖3所示，球心在O1O2的中點，半徑OA=AO22+O2O2=43+3=133，故外接球表面積為4πR2=52π3。

思路3：從翻折的角度觀察幾何體的特征。

從題意可知，本題的三棱錐A-BCD是由兩個Rt△ABC，Rt△BCD沿著BC邊翻折而成，如圖4所示。

解法3：本題是翻折成60°的二面角，從特殊位置出發，當兩個面翻折成90°的直二面角時，如圖5所示，面ABC與面BCD形成了一個墻面模型。將三棱錐A-BCD放進長方體中，如圖6所示，易知球心在體對角線AD的中點。

如圖7所示，取BC的中點M，連接MO1，MO2，易知MO1⊥BC，MO2⊥BC，即∠O1MO2為二面角A′-BC-D的平面角；而OO1，OO2分別可看作面BCD和面A′BC的法向量，則〈OO1，OO2〉=120°，那么M，O，O1，O2四點共面。

如圖8所示，在Rt△OMO1中，∠OMO1=30°，OO1=1，故OM=1cos∠OMO1=1cos30°=23。

在Rt△OMC中，MC=3，OM=23，則R2=OC2=MC2+OM2=133，

故外接球表面積為4πR2=52π3。

三、 解題反思

上述解法都需要將三棱錐放到正三棱柱和長方體模型中來解題的，對于不能放進幾何模型的題型該如何解決呢？

下面探究解決這類問題的通法通解：

如圖9所示，在球O中任取兩個相交的截面圓，記兩個交點分別為A，B，兩個截面圓的圓心分別為O1，O2，取AB的中點M，連接O1M和O2M。

由圓的垂徑定理知，O1M⊥AB，O2M⊥AB，

故∠O2MO1為兩個截面圓所成二面角的平面角，

易知OO1⊥圓面O1，OO2⊥圓面O2，∠O1OO2+∠O1MO2=π，故O，O1，O2，M四點共圓。

在四邊形OO1MO2中，∠OO1M=∠OO2M=π2，

即OM為O，O1，O2，M四點所在外接圓O3的直徑，記為2r，外接球的半徑為R，則R2=OA2=AB22+（2r）2。

即外接球球心由兩個截面圓過圓心的面的垂線的確定。

對本題而言，容易得到△ABC和△BCD為直角三角形，則這兩個三角形的外接圓的圓心均在斜邊的中點O2和O1，如圖10所示，

∵MO2=12AB=1，MO1=12BD=1，∠O1MO2=60°，則O1O2=1，

在△O1O2M中，由正弦定理得，2r=O1O2sin60°=23，

∴R2=OC2=AB22+（2r）2=（3）2+232=133，

故外接球表面積為4πR2=52π3。

四、 變式拓展

變式1：在四面體S-ABC中，AB⊥BC，AB=BC=2，SA=SC=2，SB=6，則此四面體的外接球表面積為 。

由題意可知，△ABC為直角三角形，則其外接圓的圓心在AC的中點D，△SAC為等邊三角形，則其外接圓的圓心在中線SD的三等分點O1處。如圖11所示，過D，O1分別向各自所在的平面作垂線，則球心為交點O。易知SD=3，DB=1，O1D=33，因為SB=6。在△SDB中，由余弦定理得，SB2=SD2+DB2-2DB·SD×cos∠SDB，解得cos∠SDB=-33。

因為sin∠SDO=sin∠SDB-π2=-cos∠SDB=33，所以OO1=OD1×tan∠ODO1=33×22=66。

設外接球半徑為R，則R2=SO21+OO21=32，故外接球表面積為4πR2=6π。

變式2：在四面體S-ABC中，SA⊥面ABC，∠BAC=120°，SA=AC=2，AB=1，則它的外接球的表面積為 。

解：易知SB和SC分別為Rt△ABS和Rt△ACS的斜邊，如圖12所示，分別取中點O2，O1，過O1，O2分別向各自所在的平面作垂線，則球心為交點O。如圖13所示，在四邊形OO1O2M中，∵MO2=12AB=12，MO1=12AC=1，∠O1MO2=∠BAC=120°，由余弦定理得，O1O22=14+1-2×12×1cos120°=74，即O1O2=72。

在△O1O2M中，由正弦定理得，2r=O1O2sin120°=73，

∴R2=OC2=AS22+（2r）2=12+732=103，故外接球表面積為4πR2=40π3。

另解：如圖14所示，分別找△ABC和△SAC的外接圓的圓心O2，O1，分別取中點O2，O1，過O1，O2分別向各自所在的平面作垂線，則球心為交點O。

在△ABC中，AB=1，AC=2，∠BAC=120°，由余弦定理得，BC2=1+2-2×1×2cos120°=7，即BC=7。

設△ABC的外接圓的半徑為r，由正弦定理得，2r=BCsin120°=273，則r=AO2=73，而OO2=12SA=1，故R2=OA2=（OO2）2+（AO2）2=12+732=103，

故外接球表面積為4πR2=40π3。

從本題的兩種解法看出，不管找幾何體哪個面所在的截面圓，都可以很快找到外接球球心；然后通過解三角形相關知識，求出外接球的半徑。其計算難度比建系設點以及套用模型的方法難度小，做到了從一題多解到多題一解的思維轉變。

五、 結論

通過以上例子可以看出，立體幾何問題在求解的過程中，教師要引導學生準確地畫出幾何圖形，感受圖形的幾何特征，提高直觀想象核心素養和空間想象能力。在實際求解過程中，教師要引導學生可以將空間問題平面化，將三維空間問題轉化為二維平面問題來解決，實現降維的目的，降低思維難度。

參考文獻：

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版）［S］.北京：人民教育出版社，2018.

［2］羅增儒.數學解題學引論［M］.西安：陜西師范大學出版總社，2016.