三相PWM整流器離散空間矢量無模型預測電流控制策略

摘" 要：

針對PWM整流器模型預測控制對系數參數準確性高度依賴的問題，提出一種基于離散空間矢量的無模型預測電流控制（MFPCC）策略。該策略通過矢量合成，在每個控制周期應用兩個基本矢量，提高了預測電流的準確性；通過峰谷采樣，分別測量并存儲上一控制周期兩個基本矢量作用下的電流梯度；并建立電流梯度方程，從而根據應用矢量的電流梯度進一步更新剩余6個未應用矢量的電流梯度，結合當前時刻的電流采樣值，實現未來時刻的電流預測，得到下一時刻最優的虛擬矢量。該方法不依賴于任何系統參數，且消除了傳統MFPCC策略中電流梯度更新停滯現象，降低了輸出電流諧波。最后，通過實驗和仿真驗證了所提方法的有效性和優越性。

關鍵詞：PWM整流器；無模型預測電流控制；離散空間矢量；電流梯度更新；停滯現象

DOI：10.15938/j.emc.2024.06.016

中圖分類號：TM464

文獻標志碼：A

文章編號：1007-449X（2024）06-0163-08

收稿日期： 2022-09-15

基金項目：新能源與儲能運行控制國家重點實驗室開放基金（NYB51202201697）

作者簡介：胡存剛（1979—），男，教授，博士生導師，研究方向為多電平逆變器的分析與控制；

尹" 政（1996—），男，碩士，研究方向為變流器的調制與控制；

張" 悅（1991—），女，碩士，高級工程師，研究方向為新能源并網控制與仿真；

羅" 魁（1989—），男，碩士，高級工程師，研究方向為新能源并網仿真分析；

芮" 濤（1990—），男，博士，講師，研究方向為變流器無參數預測控制；

馮壯壯（1998—），男，碩士，研究方向為逆變器模型預測控制。

通信作者：尹" 政

Model-free predictive current control of three-phase PWM rectifier based on discrete space vector

HU Cungang1，2，" YIN Zheng2，" ZHANG Yue1，" LUO Kui1，" RUI Tao3，" FENG Zhuangzhuang2

（1.State Key Laboratory of Operation and Control of Renewable Energy amp; Storage Systems， China Electric Power Research Institute， Beijing 100192， China; 2.School of Electrical Engineering and Automation， Anhui University， Hefei 230601， China; 3.School of Internet， Anhui University， Hefei 230601， China）

Abstract：

Aiming at the problem that the model predictive control of PWM rectifier is highly dependent on the accuracy of system parameters， a model-free predictive current control （MFPCC） strategy based on discrete space vector was proposed. Through vector synthesis， two basic vectors were applied in each control period to improve the accuracy of current prediction; Based on peak and valley sampling， the current gradient of the two applied basic vectors in the previous control period was measured and stored respectively; And by establishing the current gradient equations， so as to further update the current gradient of the remaining 6 non-applied vectors according to the current gradient of the applied vector. The proposed method has strong robustness， and eliminates the stagnation effect in conventional MFPCC， and reduce current harmonics. Finally， effectiveness and advantages of the proposed method are verified by experiment and simulation.

Keywords：PWM rectifier; model-free predictive current control; discrete space vector; current gradient updating; stagnation phenomenon

0" 引" 言

三相脈寬調制（pulse width modulation，PWM）整流器廣泛應用在儲能、電力傳輸及交直流微電網分布式發電等工業系統中［1］。為了實現PWM整流器的直流側輸出電壓、電網電流和功率因數的控制，已有學者研究了比例積分控制、比例諧振控制和滯環電流控制等方法。然而，這些方法動態響應慢，難以實現多目標的控制。近年來，模型預測電流控制（model predictive current control，MPCC）因其優越的動態性能、良好的多目標控制能力及簡單的約束處理等優點［2-3］，在PWM整流器控制領域得到了廣泛的關注。然而，MPCC的預測電流由系統模型和參數直接決定，當模型參數失配時，MPCC的控制性能會顯著降低［4-6］。

為了消除模型和參數的影響，基于電流梯度的無模型預測電流控制（model-free predictive current control，MFPCC）得到了諸多學者的關注［7-10］。該方法通過測量變流器矢量作用下的電流梯度值替代傳統的預測模型［7］。值得注意的是，MFPCC的控制性能會受電流梯度更新頻率的影響。當每個控制周期僅通過電流測量，更新應用矢量作用下的電流梯度，而未考慮其他未應用矢量的電流梯度時，會導致PWM的輸出電流存在電流尖峰。

為了提高電流梯度的更新頻率，文獻［8］在控制中設置了更新頻率。在該方法中，如果某個電流梯度在50個控制周期內沒有被更新，它對應的矢量將在下一個控制周期被使用，其電流梯度也會被隨之更新。然而，這種方法會頻繁的使用非最優矢量，從而降低電流性能。文獻［9］利用過去3個控制周期獲得的電流梯度對剩余的梯度進行更新。然而，該方法只有在過去3個控制周期應用的矢量不同時才會生效。文獻［10］根據矢量幅值更新剩余矢量的電流梯度。文獻［11］簡化了數學模型，建立了連續兩個控制周期的電流梯度關系，并根據此關系更新剩余矢量的電流梯度。然而，該方法在連續兩個周期應用的矢量相同時會失效。

傳統MFPCC的另一個問題是每個控制周期僅使用變換器的一個基本矢量，導致開關頻率較低，電流紋波較大。為了解決這個問題，文獻［12-13］提出了基于虛擬矢量的MFPCC，每個虛擬矢量由2個或3個基本矢量合成。為了獲得每個基本矢量作用下的電流梯度，這些方法需要在一個控制周期內根據每個矢量的作用時間進行多次采樣，其增加了控制系統的復雜性。此外，這些方法每個控制周期僅更新應用矢量的電流梯度，電流梯度的更新頻率較低。

本文針對三相PWM整流器提出一種基于離散空間矢量（discrete space vector，DSV）的改進MFPCC方法。該方法在每個控制周期應用2個基本矢量，可以有效降低電流紋波和THD。此外，提出一種改進的電流梯度更新方法，完全消除傳統方法停滯現象及其導致的電流尖峰。在所提的更新方法中，建立電流梯度方程組，可以計算獲得應用虛擬矢量對應的2個基本矢量的電流梯度；并根據這2個電流梯度更新剩余6個未應用基本矢量的電流梯度。

1" 傳統三相PWM整流器MFPCC

1.1" 三相PWM整流器數學模型

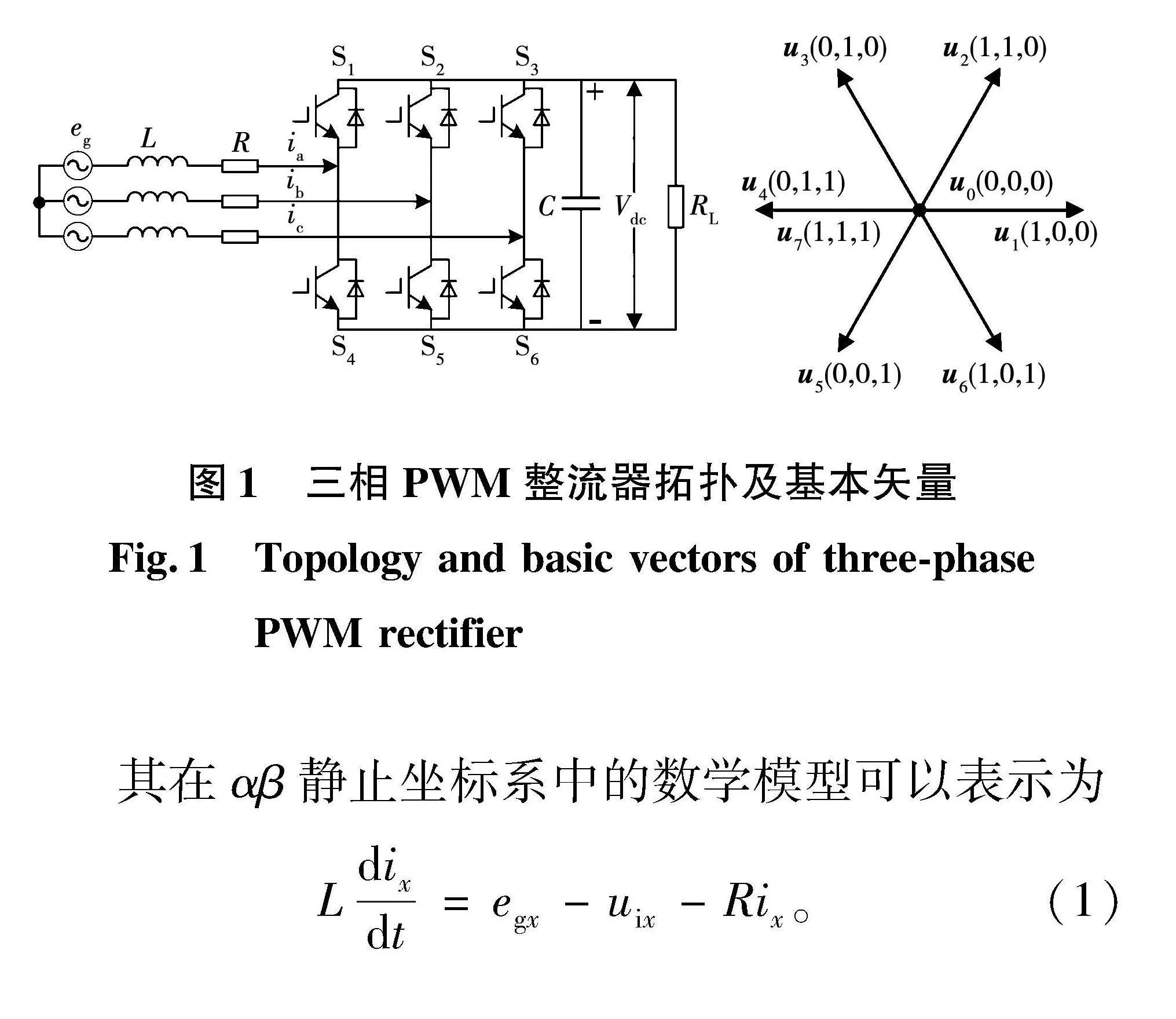
圖1給出了典型的三相PWM整流器拓撲結構及其產生的8個基本矢量。

其在αβ靜止坐標系中的數學模型可以表示為

Ldixdt=egx－uix－Rix。（1）

式中：x∈{α，β}，uix為αβ坐標系下的逆變器輸出電壓矢量；ix為αβ坐標系下的逆變器輸出電流矢量；egx為αβ坐標系下的電網電壓矢量；L為濾波電感；R為濾波電感上的寄生電阻。根據前向歐拉法，式（1）可以離散為

ix（k+1）=ix（k）+TsL［egx（k）－uix（k）－Rix（k）］Δix（k）。（2）

式中：Ts為控制周期；Δix（k）為電壓矢量uix（k）作用下的電流梯度。根據式（2）可以得知，MPCC的電流預測依賴于逆變器參數的準確性。然而，逆變器的參數可能因測量誤差而不準確，或因工作條件的變化而變化。這種參數的不確定性會導致電流預測誤差，降低電流性能。

1.2" 傳統MFPCC基本原理

為了消除模型參數對MPCC的影響，有的學者提出了基于電流梯度的MFPCC控制方法［7］，該方法利用采樣得到的電流數據替代了傳統的預測模型。其中式（2）中的電流梯度可以改寫為

Δix（k－1）=ix（k）－ix（k－1）。（3）

在MFPCC中，采樣獲得電流梯度與應用的電壓矢量一一對應，并被存儲在查詢表（look-up table，LUT）中用于電流預測。因此，（k+1）時刻的預測電流可以表示為

ix（k+1）=ix（k）+Δix（k）。（4）

傳統的MFPCC方法在每個控制周期只能更新當前電壓矢量作用下的電流梯度值，如圖2所示，對于未使用的矢量，其對應的電流梯度值則無法更新，這種更新停滯現象將導致預測的不準確性。此外，其在每個控制周期只采用一個電壓矢量，導致逆變器開關頻率低，輸出電流紋波大。

2" 基于離散空間矢量的MFPCC

為了解決上述問題，本文提出了一種改進的DSV-MFPCC，所提方法包括4個部分：DSV-MFPCC的基本原理、電流梯度更新方法、停滯消除及所提DSV-MFPCC的實現過程。

2.1" DSV-MFPCC基本原理

根據伏秒平衡原理，使用8個基本矢量生成12個虛擬矢量，并表示為

usi=0.5um+0.5un。（5）

式中：usi為電壓矢量組合，i∈{1，2，…，12}，12個電壓矢量組合分別由（u0，u1）、（u7，u2）、（u0，u3）、（u7，u4）、（u0，u5）、（u7，u6）、（u1，u2）、（u2，u3）、（u3，u4）、（u4，u5）、（u5，u6）、（u6，u1）合成；um和un為2個基本電壓矢量。

所提方法在每個控制周期應用兩個基本電壓矢量。基于所選虛擬矢量對應的電流梯度及其作用時間，可以計算出預測電流。因此，（k+1）時刻和（k+2）時刻的預測電流可以分別表示為：

ix（k+1）=ix（k）+0.5（Δiumx（k）+Δiunx（k））;（6）

ix（k+2）=ix（k+1）+0.5（Δiumx（k+1）+Δiunx（k+1））。（7）

在執行MFPCC時，需要將12個虛擬矢量對應的電流梯度代入式（7），并將得到12個預測電流代入下式所示的價值函數進行評估，最終選擇使價值函數最小的電壓矢量作為最優電壓矢量，并將其作用在下一個控制周期：

G=（irefα－iα（k+2））2+（irefβ－iβ（k+2））2。（8）

式中下標“ref”代表電流的參考值。

2.2" 電流梯度更新方法

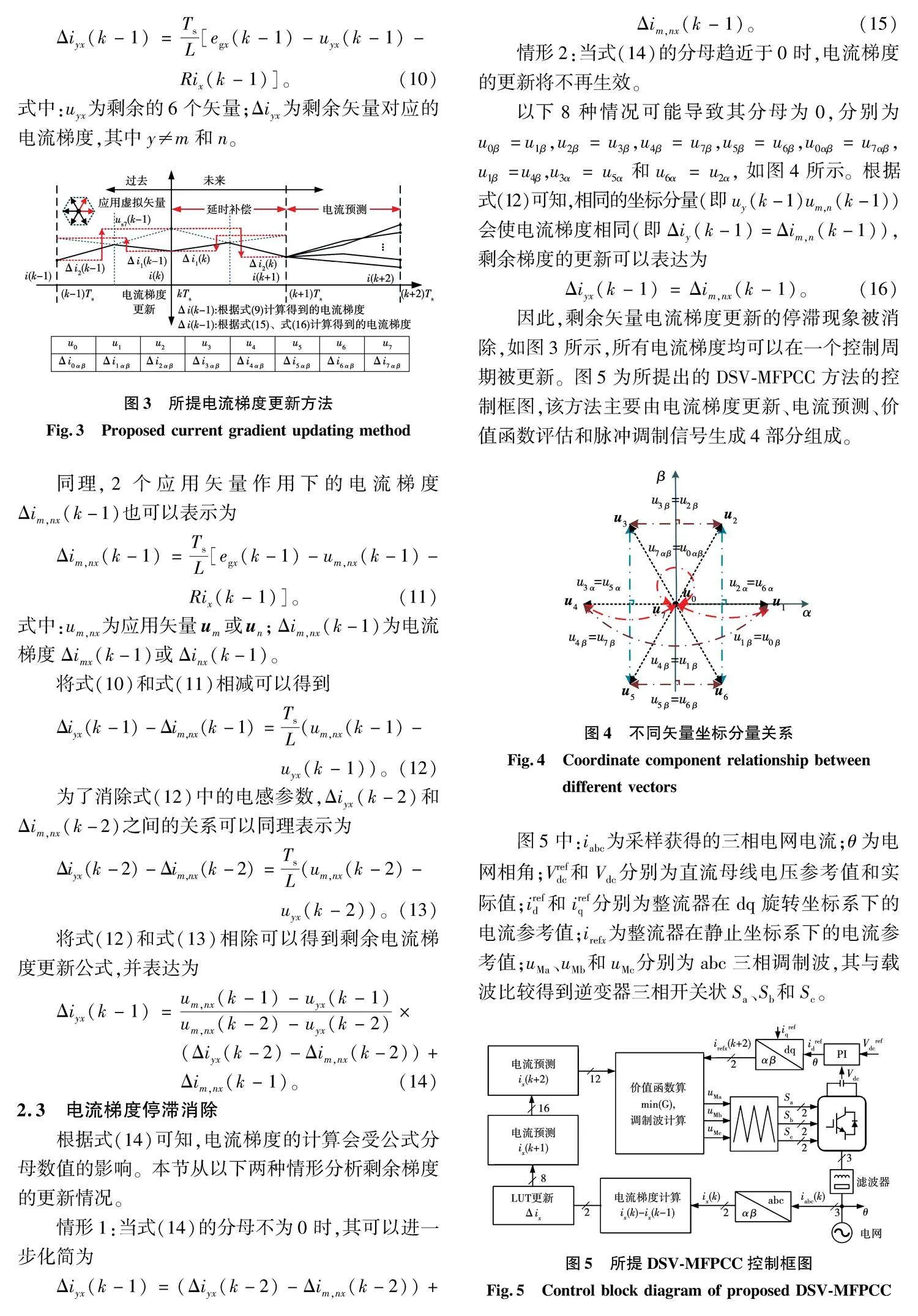
當（k-1）時刻和k時刻應用的虛擬矢量由2個基本矢量um和un組成時，如圖3所示，由于其作用時間均為0.5Ts，可以在每個控制周期的中點和末端設置兩個采樣點，分別測量電流梯度Δimx（k-1）和Δinx（k-1）并分別表示為：

Δimx（k－1）=2（ix（k）12－ix（k－1））;

Δinx（k－1）=2（ix（k）－ix（k）12）。（9）

此外，為了更新剩余6個矢量對應的電流梯度，需要建立其與上述2個應用矢量電流梯度之間的關系。根據式（2）可以將剩余矢量作用下的電流梯度Δiyx（k-1）表示為

Δiyx（k－1）=TsL［egx（k－1）－uyx（k－1）－

Rix（k－1）］。（10）

式中：uyx為剩余的6個矢量；Δiyx為剩余矢量對應的電流梯度，其中y≠m和n。

同理，2個應用矢量作用下的電流梯度Δim，nx（k-1）也可以表示為

Δim，nx（k－1）=TsL［egx（k－1）－um，nx（k－1）－

Rix（k－1）］。（11）

式中：um，nx為應用矢量um或un；Δim，nx（k-1）為電流梯度Δimx（k-1）或Δinx（k-1）。

將式（10）和式（11）相減可以得到

Δiyx（k－1）－Δim，nx（k－1）=TsL（um，nx（k－1）－uyx（k－1））。（12）

為了消除式（12）中的電感參數，Δiyx（k-2）和Δim，nx（k-2）之間的關系可以同理表示為

Δiyx（k－2）－Δim，nx（k－2）=TsL（um，nx（k－2）－uyx（k－2））。（13）

將式（12）和式（13）相除可以得到剩余電流梯度更新公式，并表達為

Δiyx（k－1）=um，nx（k－1）－uyx（k－1）um，nx（k－2）－uyx（k－2）×

（Δiyx（k－2）－Δim，nx（k－2））+

Δim，nx（k－1）。（14）

2.3" 電流梯度停滯消除

根據式（14）可知，電流梯度的計算會受公式分母數值的影響。本節從以下兩種情形分析剩余梯度的更新情況。

情形1：當式（14）的分母不為0時，其可以進一步化簡為

Δiyx（k－1）=（Δiyx（k－2）－Δim，nx（k－2））+

Δim，nx（k－1）。（15）

情形2：當式（14）的分母趨近于0時，電流梯度的更新將不再生效。

以下8種情況可能導致其分母為0，分別為u0β=u1β，u2β=u3β，u4β=u7β，u5β=u6β，u0αβ=u7αβ，u1β=u4β，u3α=u5α和u6α=u2α，如圖4所示。根據式（12）可知，相同的坐標分量（即uy（k-1）um，n（k-1））會使電流梯度相同（即Δiy（k-1）=Δim，n（k-1）），剩余梯度的更新可以表達為

Δiyx（k－1）=Δim，nx（k－1）。（16）

因此，剩余矢量電流梯度更新的停滯現象被消除，如圖3所示，所有電流梯度均可以在一個控制周期被更新。圖5為所提出的DSV-MFPCC方法的控制框圖，該方法主要由電流梯度更新、電流預測、價值函數評估和脈沖調制信號生成4部分組成。

圖5中：iabc為采樣獲得的三相電網電流；θ為電網相角；Vrefdc和Vdc分別為直流母線電壓參考值和實際值；irefd和irefq分別為整流器在dq旋轉坐標系下的電流參考值；irefx為整流器在靜止坐標系下的電流參考值；uMa、uMb和uMc分別為abc三相調制波，其與載波比較得到逆變器三相開關狀Sa、Sb和Sc。

3" 仿真和實驗驗證

3.1" 仿真驗證

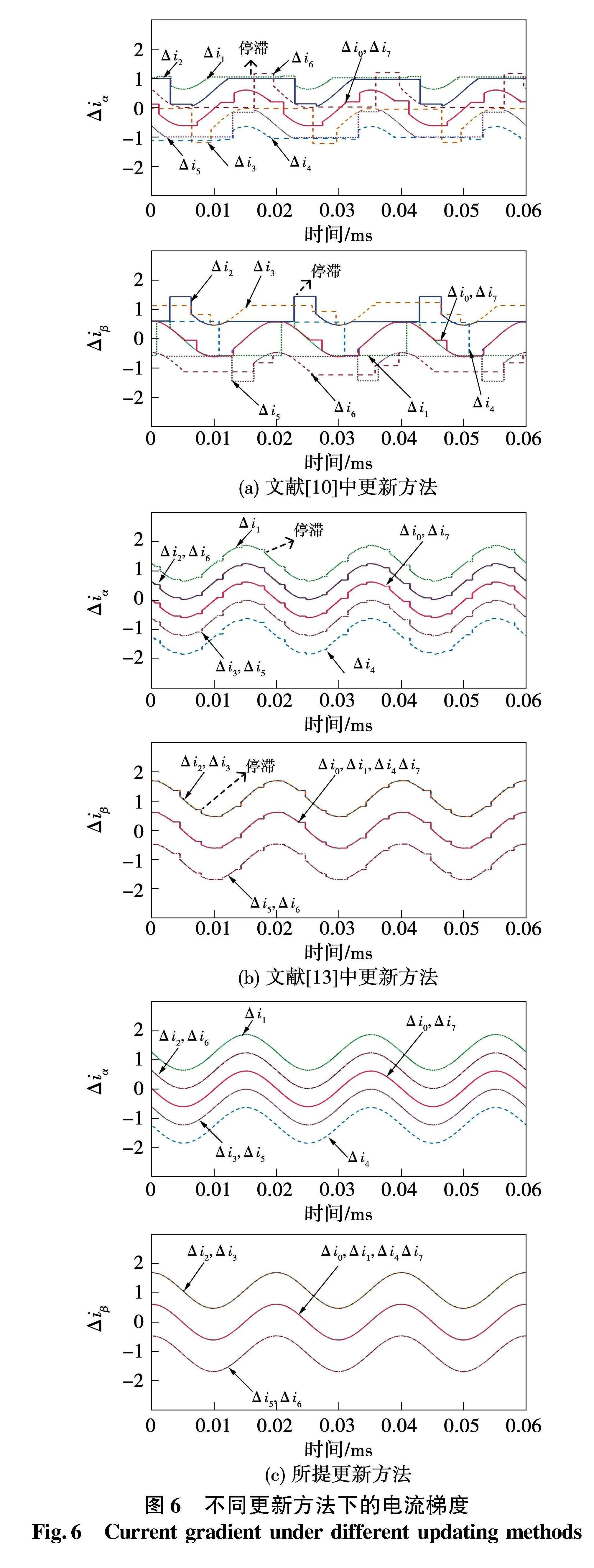
圖6為文獻［10］中電流梯度更新方法、文獻［13］中電流梯度更新方法和所提更新方法的仿真結果。

圖6（a）為文獻［10］更新方法下的電流梯度波形，在該方法中，每個控制周期僅更新應用電壓矢量的電流梯度，而剩余的電流梯度保持上一個控制周期的舊值。如圖6（b）所示，當使用文獻［13］中的更新方法時，停滯現象減少。然而，Δiα和Δiβ中的停滯現象無法完全消除。圖6（c）為所提更新方法的電流梯度波形，可以看出所有電壓矢量的電流梯度在每個控制周期都會更新，更新停滯現象完全消除。其中，在α軸中有五條曲線，在β軸中有3條曲線，這是因為Δi2α=Δi6α，Δi3α=Δi5α，Δi0α=Δi7α，Δi2β=Δi3β，Δi5β=Δi6β及Δi0β=Δi7β=Δi4β=Δi1β。

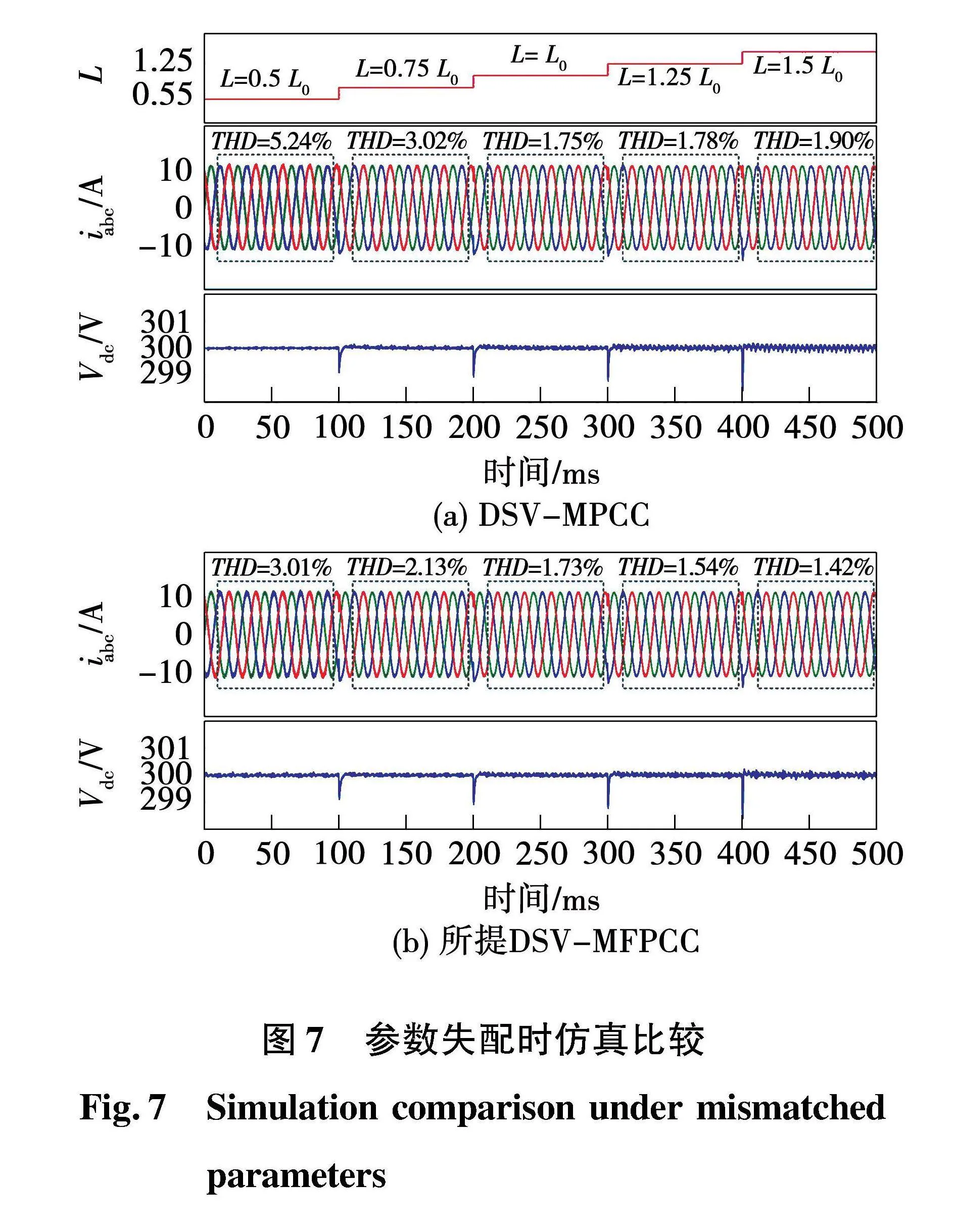
圖7為電感實際參數發生變化，控制參數不變時，DSV-MPCC和所提DSV-MFPCC的電流THD及直流側輸出電壓仿真結果。由圖7（a）可以看出，當電感的實際參數分別為控制參數的50%、75%、125%、150%時，DSV-MPCC的電流THD較參數準確時分別增大199.4%、72.6%、1.7%和8.6%，同時，系統直流側輸出電壓紋波變大。如圖7（b）所示，所提DSV-MFPCC方法參數魯棒性較好，在參數失配時電流THD較DSV-MPCC均有所降低，尤其在實際參數為控制參數的50%時。

3.2" 實驗驗證

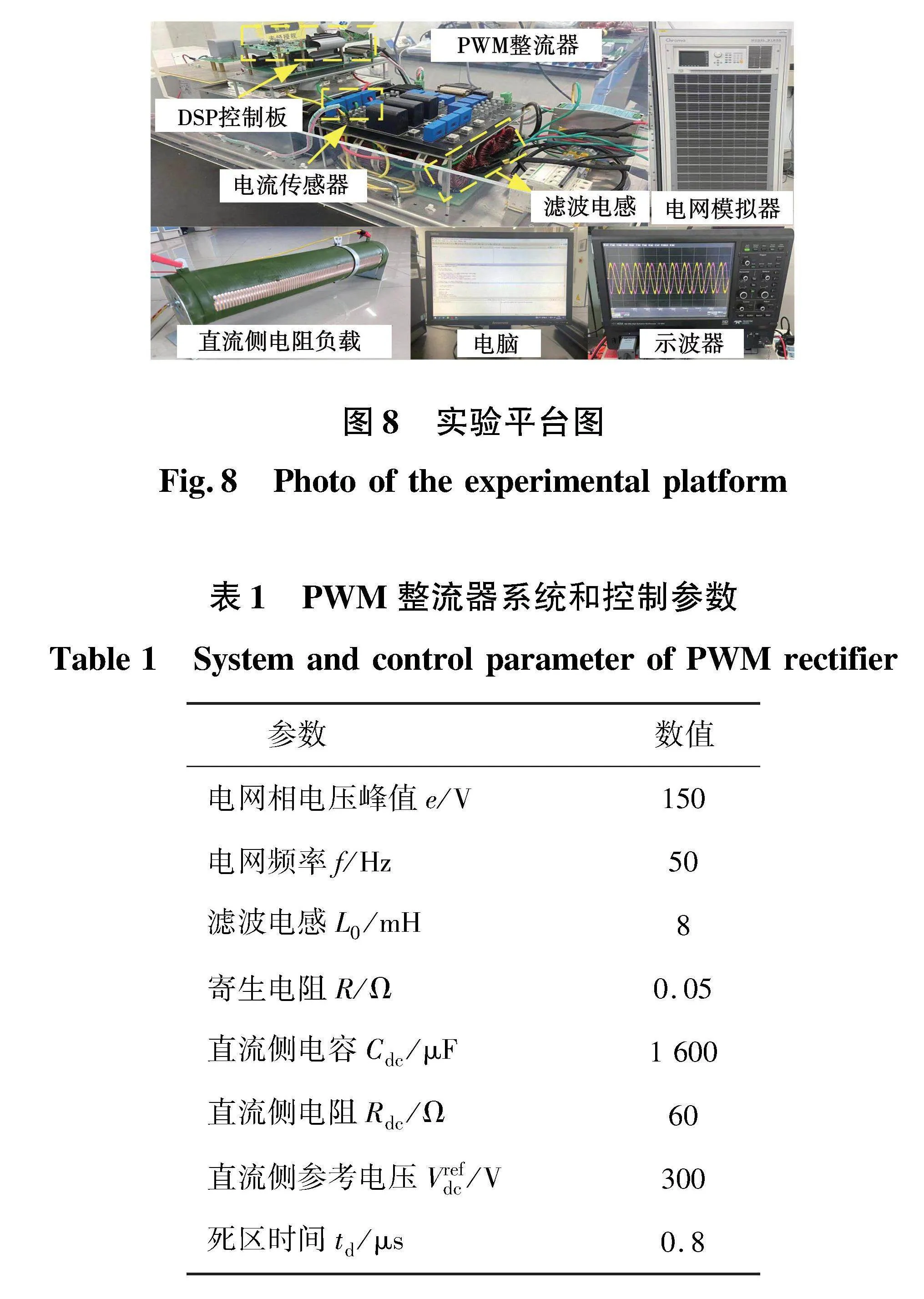
為了驗證所提DSV-MFPCC方法的有效性，搭建了兩電平PWM整流器實驗平臺，如圖8所示。其包括直流電壓源、三相并網逆變器、濾波電感和交流電壓源。所有控制方案均在TMS320F28335中實現，系統和控制參數如表1所示。示波器型號為LeCroy-HDO4034。電流探頭型號為LeCroy-CP150。

3.2.1" 魯棒性能驗證

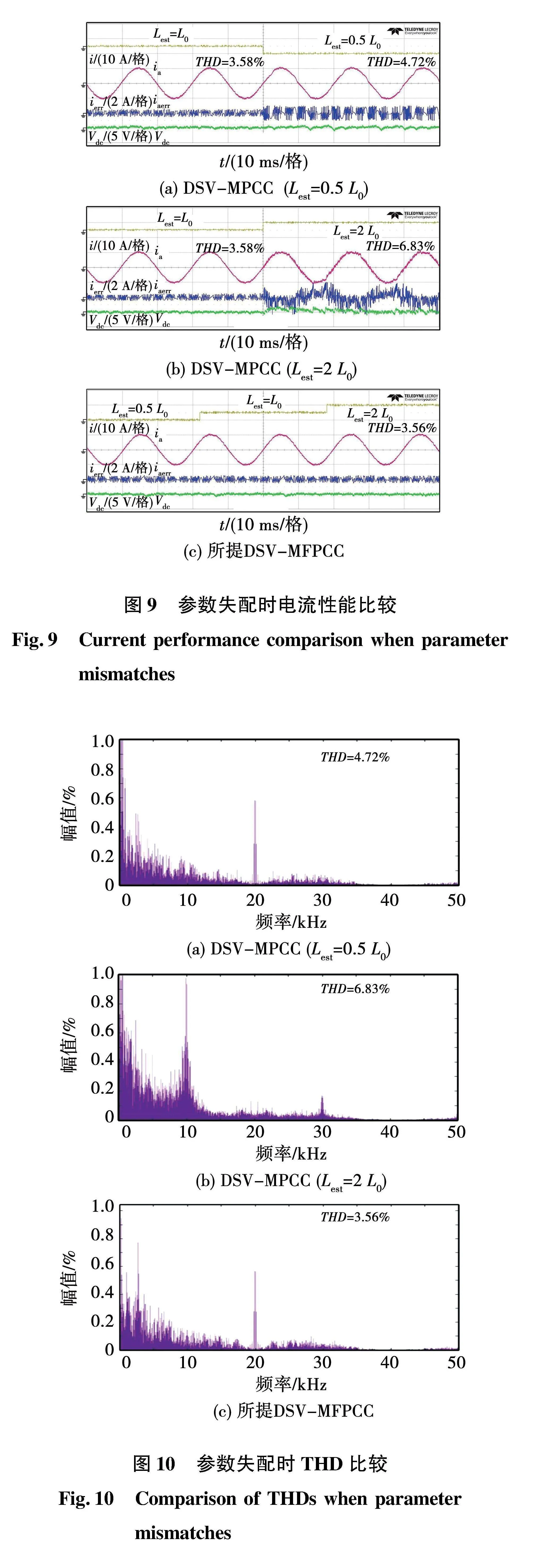
圖9比較了參數失配時DSV-MPCC和所提DSV-MFPCC的電流紋波、THD、預測誤差及直流側輸出電壓。由圖9（a）可以看出，當電感的控制參數突變為實際參數的50%時，DSV-MPCC的輸出電流紋波、THD、電流預測誤差及直流側輸出電壓紋波均變大，其中THD由3.58%增加為4.72%；當電感的控制參數突變為實際參數的2倍時，DV-MPCC輸出性能也隨之變差，其中THD由3.58%增加為6.83%。如圖9（c）所示，所提DSV-MFPCC方法輸出性能不受參數的影響，THD保持為3.56%，與DSV-MPCC在兩種失配條件下的THD相比分別降低了1.14%及3.25%。3種方法的THD頻譜如圖10所示，驗證了所提方法具有良好的參數魯棒性。

3.2.2" 電流梯度更新驗證

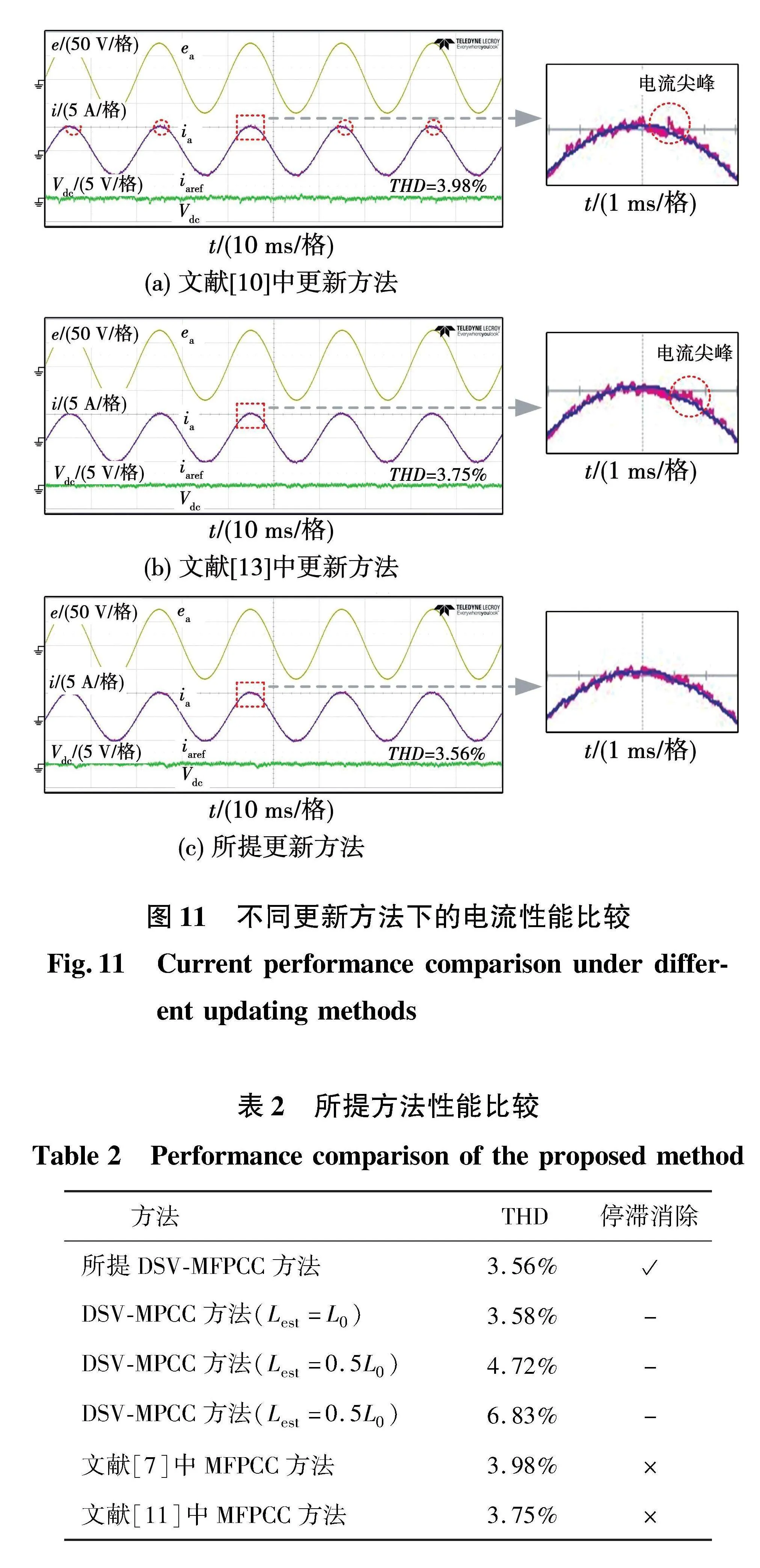
為了有效的比較電流梯度停滯現象對電流性能的影響，文獻［7］和文獻［11］中的更新方法被應用在離散空間矢量的條件下并與所提更新方法進行比較。如圖11（a）所示，由于文獻［7］中的更新方法存在明顯的停滯現象，導致電流紋波和直流電壓紋波存在較多的電流尖峰。如圖11（b）所示，當使用文獻［11］中的更新方法時，雖然電流尖峰被有效改善，但由于停滯現象沒有完全消除，電流尖峰仍然存在。與文獻［7］和文獻［11］的更新方法相比，所提方法完全消除了停滯現象，因此其電流紋波和直流側電壓紋波最低，驗證所提更新方法的有效性。所提方法的性能比較如表2所示。

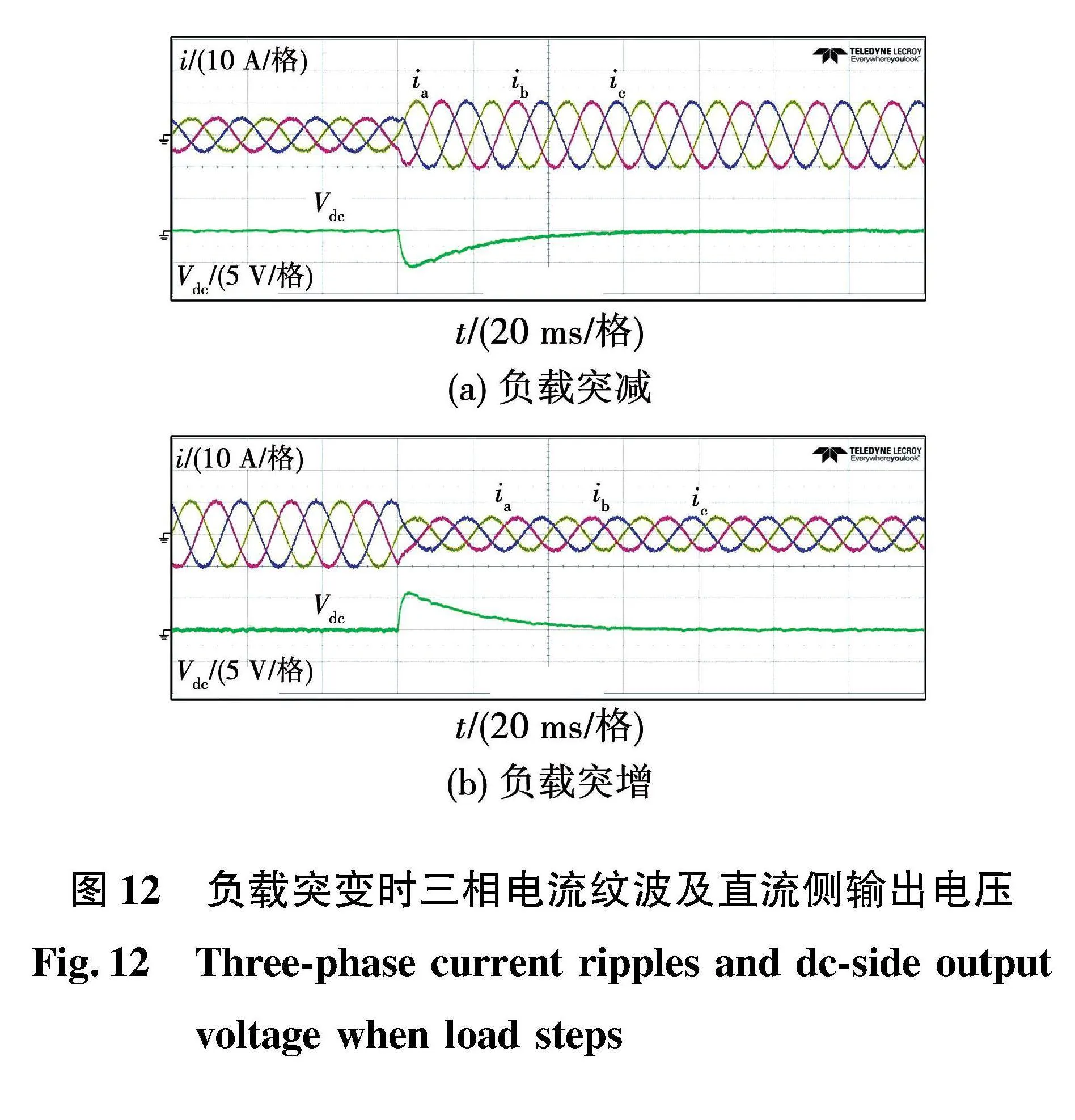
3.2.3" 動態性能驗證

圖12給出了所提方法在負載突變下的三相電流及直流側輸出電壓波形，突減負載由120 Ω突變為60 Ω，突加負載由60 Ω突變為120 Ω。由圖12（a）可以看出，負載突減時，直流電壓調節時間為63 ms，電壓跌落為2%；由圖12（b）可以看出，負載突增時，直流電壓調節時間為59 ms，電壓超調為2.5%。

4" 結" 論

本文提出了一種基于電流梯度全更新的離散空間矢量MFPCC方法，并在三相并網逆變器平臺實驗測試。結果表明，所提方法具有以下優點：

1） 該方法在每個控制周期內使用兩個電壓矢量，減小了輸出電流的紋波和THD。

2） 它不依賴于任何模型參數，具有良好的參數魯棒性，并在參數準確的條件下實現了與離散空間矢量MPCC相近的控制性能。

3） 該方法提出了一種先進的電流梯度更新方法，完全消除了電流梯度停滯現象及其導致的電流尖峰，進一步改善了電流質量。

后續研究可以通過改進矢量組合實現雙矢量、三矢量MFPCC控制，進一步減小電流紋波；或將其應用于LCL濾波的PWM整流器中，進一步研究高階系統下的參數魯棒性問題。

參 考 文 獻：

［1］" 王占擴，張永昌，童朝南.一種改進的三相PWM整流器模型預測控制方法研究［J］.電機與控制學報，2020，24（7）：73.

WANG Zhankuo， ZHANG Yongchang， TONG Chaonan. Improved model predictive direct power control for three-phase PWM rectifier ［J］. Electric Machine and Control，2020，24（7）：73.

［2］" 郭磊磊，金楠，許烈.采用混合電壓矢量預選和參考電壓預測的逆變器共模電壓尖峰消除方法［J］.中國電機工程學報，2018，38（17）：5167.

GUO Leilei， JIN Nan， XU Lie. Common-mode voltage spikes elimination method for inverters using hybrid voltage vector preselection and reference voltage prediction ［J］. Proceedings of the CSEE， 2018， 38（17）： 5167.

［3］" 朱文杰，陳昌松，段善旭．一種基于離散空間矢量調制的 Vienna 整流器模型預測控制方法［J］．中國電機工程學報， 2019， 39（20）： 6008．

ZHU Wenjie， CHEN Changsong， DUAN Shanxu． A model predictive control method with discrete space vector modulation of vienna rectifier［J］．Proceedings of the CSEE，2019，39（20）：6008．

［4］" HU Cungang， YIN Zheng， RUI Tao， et al. A novel double-voltage-vector model-free predictive current control method for two-level voltage source inverters［J］. IEEE Transactions on Industrial Electronics， 2023， 70（6）： 5872.

［5］" 胡存剛， 尹政， 芮濤， 等. 計及采樣擾動抑制的電壓源逆變器三矢量無模型預測電流控制方法［J］. 中國電機工程學報， 2024， 44（6）： 2408.

HU Cungang， YIN Zheng， RUI Tao， et al. Triple-vector model-free predictive current control method for voltage source inverter with sampling disturbance suppression［J］. Proceedings of the CSEE， 2024，44（6）：2408.

［6］" YIN Zheng， DENG Fujin， GHANEM A， et al. PLPR-based predictive control for LCL-filtered voltage source inverters［J］. IEEE Transactions on Power Electronics， 2024， 39（6）： 7468.

［7］" LIN Chengkai， LIU Tianhua， YU Jente， et al. Model-free predictive current control for interior permanent-magnet synchronous motor drives based on current difference detection technique［J］. IEEE Transactions on Industrial Electronics， 2014， 61（2）：667.

［8］" LIN Chengkai， YU Jente， LAI Yenshin， et al. Improved model-free predictive current control for synchronous reluctance motor drives［J］. IEEE Transactions on Industrial Electronics， 2016， 63（6）： 3942.

［9］" CARLET P G， TINAZZI F， BOLOGNANI S， et al. An effective model-free predictive current control for synchronous reluctance motor drives［J］. IEEE Transactions on Industry Applications， 2019， 55（4）： 3781.

［10］" YU Feng， ZHOU Chenhui， LIU Xing， et al. Model-free predictive current control for three-level inverter-fed IPMSM with an improved current difference updating technique［J］. IEEE Transactions on Energy Conversion， 2021，36（4）：3334.

［11］" MA Chenwei， LI Huayu， YAO Xuliang， et al. An improved model-free predictive current control with advanced current gradient updating mechanism［J］. IEEE Transactions on Industrial Electronics， 2021， 68（12）： 11968.

［12］" AGUSTIN C A， YU Jente， CHENG Yushan， et al. Model-free predictive current control for synRM drives based on optimized modulation of triple-voltage-vector［J］. IEEE Access， 2021，9： 130472.

［13］" AGUSTIN C A， YU Jente， LIN Chengkai， et al. Triple-voltage-vector model-free predictive current control for four-switch three-phase inverter-fed SPMSM based on discrete-space-vector modulation［J］. IEEE Access， 2021，9：60352.

（編輯：劉素菊）