考慮逆變器諧波耦合的牽引傳動系統機電耦合振動特性研究

摘" 要：

作為牽引傳動系統能量轉換的關鍵部件，牽引電機在電氣激勵作用下會受到各種沖擊載荷和周期激振力的作用，從而產生機電耦合振動，威脅牽引傳動系統的可靠運行。對此，基于雙慣量模型對牽引傳動系統機電耦合振動特性開展研究。首先，建立牽引電機的雙慣量模型，依據此模型對其固有頻率進行計算，并介紹了機械傳動系統的同頻受迫振動模態。其次，根據逆變器的開關特性，著重分析了脈寬調制（PWM）導致的邊帶諧波轉矩對機電耦合同頻共振的影響，探索逆變器的頻率耦合產生的間諧波對機電耦合系統的影響。接著，以傳遞函數的形式對考慮雙慣量負載的牽引傳動系統進行建模，從頻域角度對系統機電耦合共振特性進行理論分析。最后，利用硬件在環測試對所分析結果進行驗證。

關鍵詞：牽引傳動系統；機電耦合；同頻共振；雙慣量系統；邊帶諧波；感應電機

DOI：10.15938/j.emc.2024.06.011

中圖分類號：TM343

文獻標志碼：A

文章編號：1007-449X（2024）06-0109-11

收稿日期： 2023-08-03

基金項目：國家自然科學基金（52177060）

作者簡介：葛興來（1979—），男，博士，教授，博士生導師，研究方向為電力電子與電力傳動；

常" 玉（1999—），男，碩士研究生，研究方向為電力電子技術和電機驅動控制；

王帥帥（1995—），男，碩士，研究方向為交流電機驅動；

沐俊文（1995—），男，博士研究生，研究方向為機電耦合共振；

左" 運（1996—），男，博士研究生，研究方向為電力電子技術和電機驅動控制；

王惠民（1994—），男，博士，助理教授，研究方向為高性能交流電機驅動控制和牽引傳動系統可靠性分析。

通信作者：葛興來

Research on electromechanical coupling vibration characteristics of inverter-motor drive system

GE Xinglai1，" CHANG Yu1，" WANG Shuaishuai1，2，" MU Junwen1，" ZUO Yun1，" WANG Huimin1

（1. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle，Ministry of Education，Southwest Jiaotong University，Chengdu 611756，China; 2.Graduate School of Tangshan，Southwest Jiaotong University，Tangshan 063000，China）

Abstract：

As a key component of electromechanical energy transmission， the traction drive system will be subjected to various impact loads and periodic excitation forces under electrical excitation， resulting in electromechanical coupling vibration. To analyze the electromechanical coupling vibration mechanism of the subway traction drive system， the drive device was simplified， which is equivalent to a two-mass model， and its natural frequency was calculated. Considering different torque excitation forms， the vibration mode of the mechanical drive system was analyzed. Then， according to the switching characteristics of the inverter， the effects of the sideband harmonic torque generated by pulse width modulation （PWM） on the same-frequency resonance of electromechanical coupling was focused on. Then， the traction drive system considering a two-mass load was modeled in the form of a transfer function， and the electromechanical coupling resonance characteristics of the system were theoretically analyzed from the frequency domain perspective. Finally， the analyzed results are verified in a hardware-in-the-loop test system.

Keywords：traction drive system; electromechanical coupling; same frequency resonance; two-mass system; sideband harmonics; induction motor

0" 引" 言

作為牽引傳動系統能量轉換的重要組成部分［1-2］，牽引電機輸出轉矩經聯軸器、減速齒輪等裝置傳遞給輪對，驅動列車前行。一方面，機械傳動部分所引入的聯軸器、齒輪箱及其柔性懸掛裝置、軸承等柔性環節對電機輸出電磁轉矩到輪對所受扭矩的力矩傳遞過程造成延遲，引發電機和負載兩端轉速失配，進而誘發機械傳動系統的扭振［3-5］；另一方面，電氣側逆變器非線性，直流電壓二次紋波等非理想因素也會通過電機定轉子氣隙傳遞到機械側，進一步加劇機電耦合振蕩。嚴重的扭轉振動會導致軸系的塑性變形，從而導致材料疲勞，在最壞的情況下，可能導致轉子部件開裂。根據變形的程度，牽引傳動系統的運行性能可能受到永久性的影響［6-8］。牽引傳動系統扭振是由機械傳動結構的固有屬性和電氣側激勵下電磁轉矩共同作用導致的典型機電耦合共振現象。因此，以機械傳動結構為基礎，分析電氣激勵下轉矩變化對扭振的影響是探究機電耦合共振機理的關鍵。

電磁轉矩作為機械驅動裝置的驅動力矩，是引發機電耦合共振的直接來源［9］。文獻［10］針對永磁交流伺服系統，重點分析了彈性傳動裝置的機械諧振機理，證明了開環系統階躍響應會加劇機械負載的振蕩，閉環系統帶寬會影響諧振模式。荷蘭代夫特大學Max Wolfgang Winterling等［11-12］將電氣驅動系統與機械裝置以及輪軌接觸特性結合分析，認為二次濾波支路失配等電氣環節失效是發生機電耦合振蕩主要原因。進一步，文獻［11］對萬向軸驅動系統進行詳細的分析，根據理論與仿真計算了驅動系統的振動模態，并分析了電機的諧波轉矩特性，認為轉矩脈動是機電耦合振動不可忽略的激勵源。此外，針對高速列車機電耦合振動現象，文獻［13］建立了傳動系統耦合振動模型，并對系統振蕩機理和影響因素進行了詳細分析。文獻［14］采用有限元包對感應電機輸出轉矩進行瞬態分析，既考慮了電機轉子以恒定速度運行引起的諧波轉矩，又對電機空載啟動到達同步速度的機電耦合振動狀態進行了驗證。

在列車牽引傳動系統中，變流器普遍采用大功率低開關頻率供電，而控制閉環系統存在功率開關器件死區效應、采樣保持、脈沖重載更新等固有延時，這些延時環節進一步降低系統動態響應性能，增加轉矩輸出諧波含量。文獻［15］結合異步調制下牽引電機輸出轉矩諧波成分分析，發現死區時間與逆變器5、7、11等次諧波電流成正比，直接影響電機偶數次諧波轉矩，導致傳動裝置振動幅值加劇。文獻［16-17］針對電機-負載雙慣量模型，討論了變頻驅動系統的各頻次諧波轉矩與逆變器調制頻率的關系，指出了諧波轉矩頻率與機械固有頻率接近時，扭轉振動模態可能被放大，但未給出機電耦合振動發生的具體工作頻率點或速度點。

綜上，多數文獻考慮的電氣激勵形式較為單一，共振諧波轉矩來源主要為階躍轉矩指令和基頻整數次電磁轉矩諧波，分析機電耦合振動模態比較局限，難以厘清包含多種電氣激勵作用下電磁轉矩對振動模態的影響。對此，本文將分析不同的轉矩激勵形式下牽引傳動裝置的機電耦合振蕩，重點考慮逆變器調制產生的邊帶諧波轉矩，探索傳動系統中頻域分布極廣的間諧波對傳動系統的影響，推導其與機械固有頻率同頻振蕩時的關系式，補充機電耦合共振諧波轉矩的來源。建立牽引傳動系統的機電耦合模型，詳細討論邊帶諧波轉矩對機械傳動部件振動的影響。最后，利用硬件在環測試對所提出的理論分析進行有效驗證。

1" 機械驅動裝置振動分析

1.1" 驅動裝置模型構建

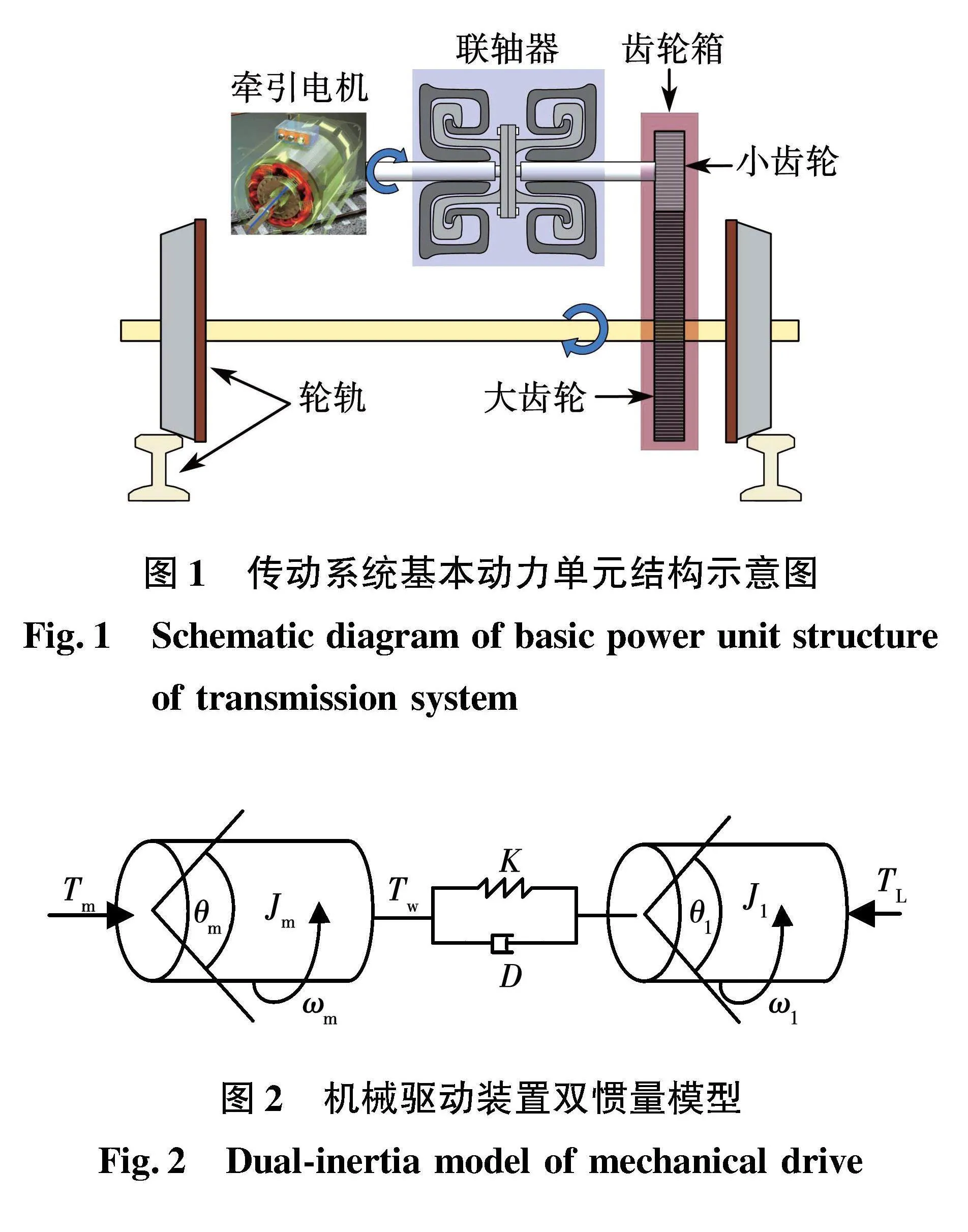
牽引傳動系統結構復雜，機械傳動裝置與電氣系統共同構成了一個機電耦合系統，基本動力單元結構如圖1所示。

根據國際標準ISO 222666-1，齒輪箱耦合橫向、扭轉和單斜齒輪軸系的軸向振動導致橫向和扭轉動力學之間的相互作用。在這種情況下，軸頸軸承可以為扭轉振動提供相當大的阻尼。由于齒輪齒的相互作用，齒輪的剛度取決于軸的角度位置和傳遞的扭矩。考慮到這些影響可能導致需要非常復雜的非線性模型，從而需要花費巨大的精力來評估軸系的動態特性。在許多情況下（例如，如果使用柔性聯軸器），扭轉-側向-軸向相互作用可以忽略。在這種情況下，軸系模型應考慮齒輪的傳動比、軸系剛度和慣性特性。并且標準指出考慮軸系扭振的機電耦合系統中，電氣系統模型一般只包含機械系統的基本信息（具有幾個自由度的軸系的總慣性或集總質量模型），將牽引傳動系統質量平均等效至傳動軸負載側，并將負載側轉動慣量與電機轉動慣量歸算至同一轉速下。最終，機械驅動裝置等效為一個僅有電機-負載的雙慣量集中質量模型，中間由具有一定剛度和阻尼的彈性軸連接，并忽略其自身慣量，如圖2所示。

當電機電磁轉矩Tm驅動電機旋轉時，傳動軸因存在彈性而發生形變，進而產生傳動軸扭矩Tw（以下簡稱“軸矩”）。軸矩Tw作為內部扭矩，一方面作為電機的負載轉矩，另一方面為負載提供驅動轉矩。在電機側，電磁轉矩Tm與軸矩Tw共同作用在電機轉動慣量Jm，使其產生加速度，在負載側，軸矩Tw與負載轉矩TL共同作用驅動負載加速，最終二者達到同一轉速。根據牛頓第二定律建立驅動裝置的動力學微分方程：

Jmθ··m+Tw=Tm；

Jlθ··l－Tw=－TL；

Tw=D（θ·m－θ·l）+K（θm－θl）。（1）

式中：Tm、Tw、TL分別為電機電磁轉矩、傳動軸扭矩、負載轉矩；D、K分別為傳動軸阻尼系數、傳動軸扭轉剛度；θm、θl分別為電機轉軸轉角、負載轉軸轉角。等效后的相關參數如表1所示。

對動力學微分方程式（1）進行拉普拉斯變換，可以得到機械驅動模型的傳遞函數模型，進而獲得電機轉速和負載轉速與電磁轉矩之間的傳遞函數分別為：

Gm（s）=ωm（s）Tm（s）=1（Jm+Jl）s×

1+2ξzωzs+1ω2zs21+2ξpωps+1ω2ps2；（2）

Gl（s）=ωl（s）Tm（s）=1（Jm+Jl）s×

Ds+KJmJlJm+Jls2+Ds+K。（3）

式中：

ωp=K（Jm+Jl）JmJl；ωz=KJl；

ξp=D2（Jm+Jl）4KJmJl;ξz=D24KJl。

其中：ωp為自然振蕩頻率；ωz為抗諧振頻率點；ξp、ξz為對應的阻尼系數。

根據式（2）可以看出，傳遞函數Gm（s）由慣性環節和二階振蕩環節兩部分組成。二階振蕩環節給傳遞函數引入了一對共軛零極點，其中由此得到上述傳遞函數Bode圖如圖3所示。可以看出，式（2）所對應傳遞函數幅值在自然振蕩頻率ωp處（約為25 Hz）迅速增加，在機械驅動裝置中表現為扭振加劇。并且，由于抗諧振頻率ωz的存在，在閉環控制中會對系統扭振有一定的抑制作用，但系統增益在諧振頻率處很大，因此抑制效果有限；而式（3）負載轉速反饋傳遞函數只存在諧振頻率ωp，由于負載轉速與電機轉速存在相位差，在經過諧振頻率ωp時相位穿越-180°，引入負載轉速反饋將會使系統發生劇烈振動并引起失穩，因此后續進行機電耦合建模僅考慮電機轉速反饋。

1.2" 同頻受迫振動

機械傳動環節同頻受迫振動是指機械環節持續受到與機械系統固有頻率相同的外部激勵所誘發的振動。考慮到電機諧波轉矩頻次多，幅值較小，因此外部激振力矩與系統固有頻率不同將不會對系統造成較大影響，這里僅考慮二者頻次相同的情況。

相對于扭轉剛度而言，阻尼系數對傳動機構影響很小，因此忽略阻尼系數［13］，假定電磁轉矩幅值為Tb，具有和系統固有頻率相同的激振力矩，施加在電機轉子上，則動力學方程為：

Jmθ··m=Tbcos（ωpt）－K（θm－θl）；

Jlθ··l=K（θm－θl）。（4）

應用拉普拉斯變換和反拉普拉斯變換可以得到電機和負載轉子位置的時域表達式為：

θm（t）=λ［1－cos（ωpt）+μtsin（ωpt）］；

θl（t）=λ1－cos（ωpt）－ωp2tsin（ωpt）；

λ=Tb（Jm+Jl）ω2p；

μ=Jlωp2Jm。（5）

該方程式表明，如果電磁轉矩以系統固有頻率的脈動施加在雙慣量系統上，那么轉子的位置軌跡可以分離為3個部分。當激勵時間超過1 s后，第3個分量將占據主導地位，第3個分量是與系統固有頻率相同的脈動，但是它的大小與時間成正比。因此，即使很小的轉矩脈動，隨著時間的推移，部件也可能產生很大的振幅，導致軸系疲勞加劇。相對應的轉速波形如圖4所示，當系統運行在125 r/min時電磁轉矩中包含與固有頻率相等的諧波轉矩（電機基頻整數次諧波），即使是在轉速閉環控制下，仍然會激發同頻共振，造成嚴重的疲勞損傷。由于同頻受迫振動的存在嚴重威脅牽引傳動系統安全穩定運行，因此下面將重點分析機電耦合同頻振動機理。

2" 電氣激勵下機電耦合同頻共振分析

2.1" 逆變器諧波特性分析

由于逆變器PWM調制的開關特性，逆變器載波頻率與調制波頻率會交互產生大量的諧波電流，使得電機在變頻調速過程中會存在各種諧波轉矩，當諧波轉矩頻率與機械自然振蕩頻率相同時，將會產生機電耦合同頻受迫振動。

2.1.1" 逆變器輸出電壓諧波特性

牽引傳動系統采用空間矢量調制策略，將直流電經三相兩電平逆變器轉換為電壓和頻率可變的三相交流電。在現有的文獻中，重點關注了低次的諧波電流和諧波電壓幅值，而實際機械軸故障主要由驅動器脈動扭矩的頻率決定。為了推導出諧波電流與諧波轉矩頻次的關系，首先對逆變器輸出電壓諧波特性進行分析，重點討論異步調制下非整數次邊帶諧波對牽引系統的影響，得到自然規則采樣下逆變器輸出線電壓的解析式，即

uAB=udc3M2cos（2πfst+π6）－4π∑∞m=1∑∞n=－∞1m×

［Dy（mMπ2）sin（m+n2π）sin（nπ3）×

sin（（mN+n）（2πfct－π3）－nπ2）］。（6）

式中：m、n分別為三角載波頻率與調制波頻率系數；M、N分別為調制度與載波比；fc、fs分別為載波頻率、調制波頻率，fc=Nfs；Dy為第一類貝塞爾函數。

式（6）包括兩部分，第一部分為逆變器輸出電壓的基波分量，第二部分為基本諧波分量。其中基本諧波分量可以進行細分，當m=0時，此時諧波為開關頻率以下的基帶諧波；當m≠0時，此時諧波為載波的邊帶諧波。不難發現，式中諧波部分包含sin（nπ/3），由于逆變器輸出的三相電壓對稱，因此不包含3的倍數次諧波；同時由于諧波分量中sin［（m+n）π/2］的存在，因此m+n≠0，且m和n應為一奇一偶的整數。根據上述分析，牽引電機的定子諧波電流頻次可以表示為

Fmn，Ia=|mfc±nfs|。（7）

式中：m、n為自然數，且滿足：

m=2i，i=0，1，2；n=6j±1，j=0，1，2；

m=2i+1，i=0，1，2；n=6j±2，j=0，1，2。

2.1.2" 諧波轉矩特性分析

逆變器以高頻“斬波”輸入直流電壓，“斬波”電壓（電流）信號包含許多與電機基頻相互作用的諧波，由此可能導致同頻次的諧波轉矩。忽略空間諧波磁動勢，認為電機的諧波轉矩是由電機磁路中的時間磁動勢引起的。這里以m=0為例，考慮6n±1次基帶諧波對諧波轉矩的影響，然后對其推廣。假定空間磁動勢只存在基波分量，則可以建立6n-1次諧波電流的時間脈動磁勢表達式為

F6n－1=32F6Φ－1sin［（6n－1）ωst+θs］。（8）

式中F6Φ-1、θs分別為6n-1次諧波合成磁動勢幅值、ωst=0時的電位移角。

同理可以獲得6n+1次諧波電流的脈動磁勢表達式為

F6n+1=32F6Φ+1sin［（6n+1）ωst－θs］。（9）

式（8）表明，6n-1次諧波電流產生的脈動磁動勢也為圓形旋轉磁動勢，其速度是基頻磁動勢的6n-1倍，方向與基波磁動勢相反；而從式（9）可知，6n+1次諧波電流磁動勢相對于基波磁動勢以6n+1倍的速度旋轉，方向與其相同。

進一步地，時間磁動勢會引起轉子電流的變化，從而產生相對應的諧波轉矩，按照產生的方式與作用的不同，可以被進一步分為穩定諧波轉矩和振動諧波轉矩。其中，穩定諧波轉矩是由相同頻次的脈動磁勢與諧波轉子電流交互產生，幅值比較下，通常不予考慮。振動諧波轉矩是由不同頻次的脈動磁勢與諧波轉子電流交互產生的，且存在的含量較多，對電機轉矩脈動影響較大。以6n-1次脈動磁勢產生的諧波轉子電流為例，可得到異步牽引電機每相轉矩的瞬時表達式為：

TA6n－1=np2πfs2Egsin（ωst）×2Ir6n－1sin［（6n－1）ωst－Φn］;（10）

TB6n－1=np2πfs2Egsin（ωst－2π3）×

2Ir6n－1sin（6n－1）ωst－Φn+2π3；（11）

TC6n－1=np2πfs2Egsin（ωst－4π3）×

2Ir6n－1sin（6n－1）ωst－Φn－2π3。（12）

式中：Ir6n-1為6n-1次轉子電流歸算值；Eg為電動勢；Φn為電動勢與對應頻次電流夾角。

對式（10）～式（12）化簡求和，可得到電機諧波轉矩的表達式為

T6n－1=3np2πfsIr6n－1Egcos［6nωst+π－Φn］。（13）

由式（13）可知，6n-1次脈動磁勢會產生6n次諧波轉矩。同理，對6n+1次脈動磁勢產生的諧波轉矩進行分析，對應的表達式如下：

T6n+1=3np2πfsIr6n+1Egcos［6nωst－Φn］。（14）

綜上分析可知，在m=0時，6n±1次的定子電流會產生6n次的諧波轉矩，推廣至m≠0的時候，可以得到電機諧波轉矩頻次的表達式為

Fxy，Te=|xfc±yfs|。（15）

經整理后，x、y和m、n分別滿足：

x=2i，i=0，1，2；

y=6j，j=0，1，2。

x=2i+1，i=0，1，2;y=3（2j+1），j=0，1，2；

m=x；n=y±1。

2.2" 電氣激勵下諧波轉矩分布及頻率轉移特性

在仿真平臺中搭建基于異步調制的異步電機牽引傳動系統仿真模型，設定恒定基波頻率50 Hz。電機額定功率為190 kW，直流側電壓為1 500 V，開關頻率1 kHz，定轉子電阻分別為0.15和0.081 Ω，定轉子電感分別為32.24和32.42 mH，定轉子互感為31.29 mH。

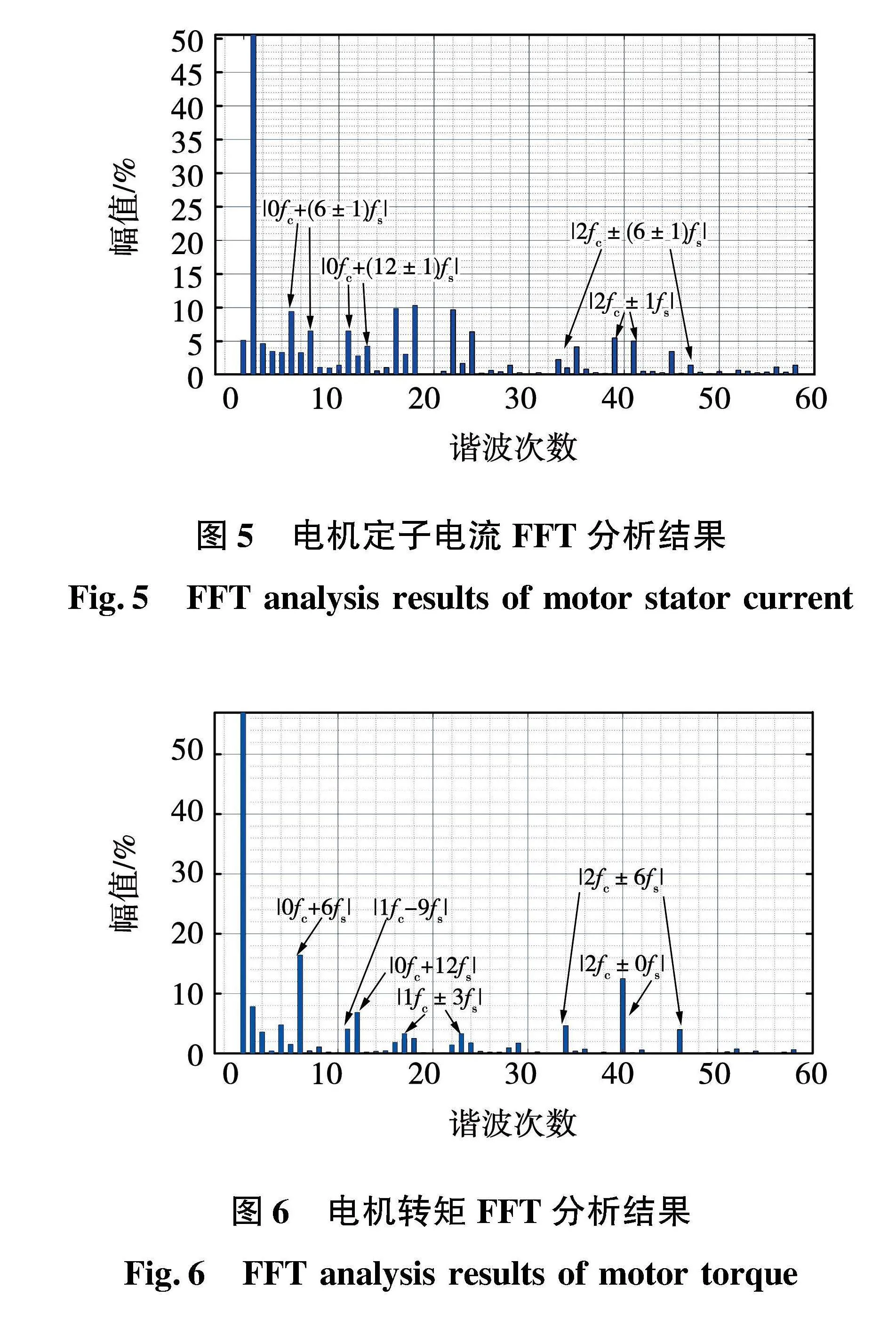
在電機達到穩態之后，分別對電機定子電流與電磁轉矩進行快速傅里葉變換（fast Fourier transform，FFT）分析，對應的諧波頻譜圖分別如圖5和圖6所示。可以看出，諧波轉矩和諧波電流主要分布在低頻以及開關頻率整數倍的邊帶處。對于諧波轉矩，主要以6、12次基波頻率、1倍開關頻率加減3倍基波頻率、2倍開關頻率以及2倍開關頻率加減6倍基波頻率為主；而電機諧波電流與諧波轉矩相對應，分布在諧波轉矩兩側，即一個諧波轉矩由相鄰頻次的兩個諧波電流產生。同時該頻譜的諧波分布基本滿足上述公式。

同樣地，在閉環矢量控制系統中仍然存在載波頻率與調制波頻率的耦合特性關系。由于逆變器的開關特性，會引入載波頻率整數倍的邊帶諧波，這里將其視為擾動，以m=1為例，分析特定基波頻率fs下電機輸出轉矩的諧波分布。根據逆變器輸出電壓的奇次邊帶諧波可知，開關頻率會與6倍的基波頻率進行耦合并向外延伸，由此可以得到矢量控制方式下不同變量的頻率轉移特性，如圖7所示。

一般來說，諧波耦合分量均為對稱分量，為方便分析，將各頻次諧波采用雙邊傅里葉變換進行展開，以正負頻率進行表示，其中，直流分量以上為負頻率耦合部分，直流分量以下為正頻率耦合部分。在Park變換方式下，電壓分量會以基波頻率產生的相位角進行旋轉，由此可以得到d-q軸坐標系下電流與轉子磁鏈的頻率考慮耦合分量，且二者諧波分量頻次一致。對于電磁轉矩而言，在穩態條件下，其值為q軸電流分量與d軸轉子磁鏈分量乘積，而諧波分量主要考慮q軸電流諧波分量與轉子磁鏈直流分量作用的結果，因此可以得到牽引電機轉矩的諧波分布。當諧波轉矩頻率與機械自然振蕩頻率相同，即可獲得同頻振蕩點，例如當+fc-27fs=25 Hz時，可以求解得到fs=36.11 Hz，與開環分析結果一致。對于偶數次邊帶諧波分析方法類似，這里不再贅述。

3" 機電耦合振蕩機理分析

牽引電機采用和諧號CRH3牽引電機，參數如表2所示［19］。

牽引電機在恒速運行工況下，電磁轉矩僅與q軸電流有關，因此可將整個控制系統簡化為等效模型，如圖8所示。該模型包含速度外環、電流內環以及機械環節。綜合考慮采樣延時、計算延時、逆變器死區效應對系統的影響，將數字控制環節等效為一階慣性傳遞函數，即

D（s）=1Tds+1。（16）

圖8中：kpn、kin為速度環調節參數；kpq和kiq為電流環調節參數；Td為控制延遲參數；F、kt為轉矩與電流變換系數、電能變換電路與電機等效增益；Gm（s）為機械傳動環節傳遞函數。

由于高階的系統不利于清晰分析系統的性能，本節對機械傳動環節還是按照雙慣量模型進行處理。通過對該理論模型的推導，可以得到整個系統的開環傳遞函數為

G（s）=（kpn+kins）Giclose（s）Gm（s）。（17）

式中

Giclose（s）=kt（kpqs+kiq）Tds2+（1+kpqktF）s+kiqktF。

其中Giclose（s）為電流閉環傳遞函數。

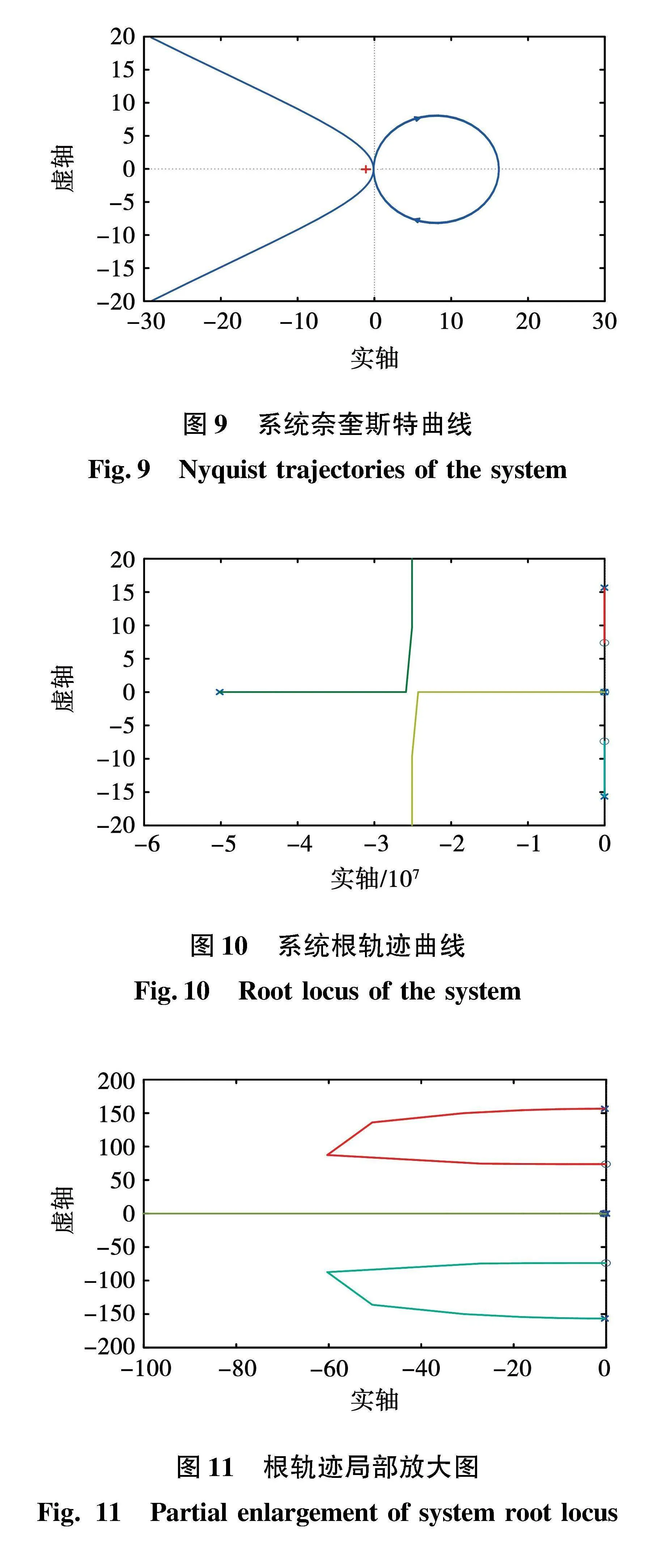
根據開環傳遞函數，將其化為標準形式，分別繪制出系統的Nyquist圖與根軌跡圖，如圖9～圖11所示。由于該開環傳遞函數為最小相位系統，Nyquist圖并未穿越（-1，j0）點，因此該系統是穩定的。而從根軌跡圖中可以看出，該系統包含6個極點和4個零點。其中，在負實軸存在1個極點，遠離虛軸，該極點是由電流閉環傳函Giclose（s）引起的。另外，圖中還存在1對共軛復數根形式的零極點，將其放大如圖11所示，可知這對零極點是由機械環節引起的，并且接近虛軸，使系統處于欠阻尼狀態，當電機諧波轉矩頻次與共軛極點頻率相同時，將會引發機電耦合同頻振蕩；另外在原點處存在2個極點，靠近虛軸的實軸上存在2個零點和1個極點，且零極點近似重合，這是由電流閉環傳函和速度調節器帶來的，一般不會對系統穩定性造成影響。

由根軌跡的定義可知，隨著開環增益的增大，雙慣量環節的共軛極點將移動至共軛零點，系統將由自然振蕩頻率變為抗諧振頻率，與理論分析結果一致。并且，在開環增益較小時，根軌跡與雙慣量自然振蕩頻率接近，靠近虛軸，隨著開環增益的增大，根軌跡將向左半平面移動，系統的阻尼系數稍有增加，系統將會處在一個較為穩定的范圍。但是，在大多增益范圍之內，根軌跡都與機械環節的自然振蕩頻率接近，轉矩或負載擾動均會引起機械傳動結構振蕩，尤其在激勵轉矩與自然振蕩頻率相同時，將會引起機電耦合同頻振蕩。

4" 硬件在環測試驗證

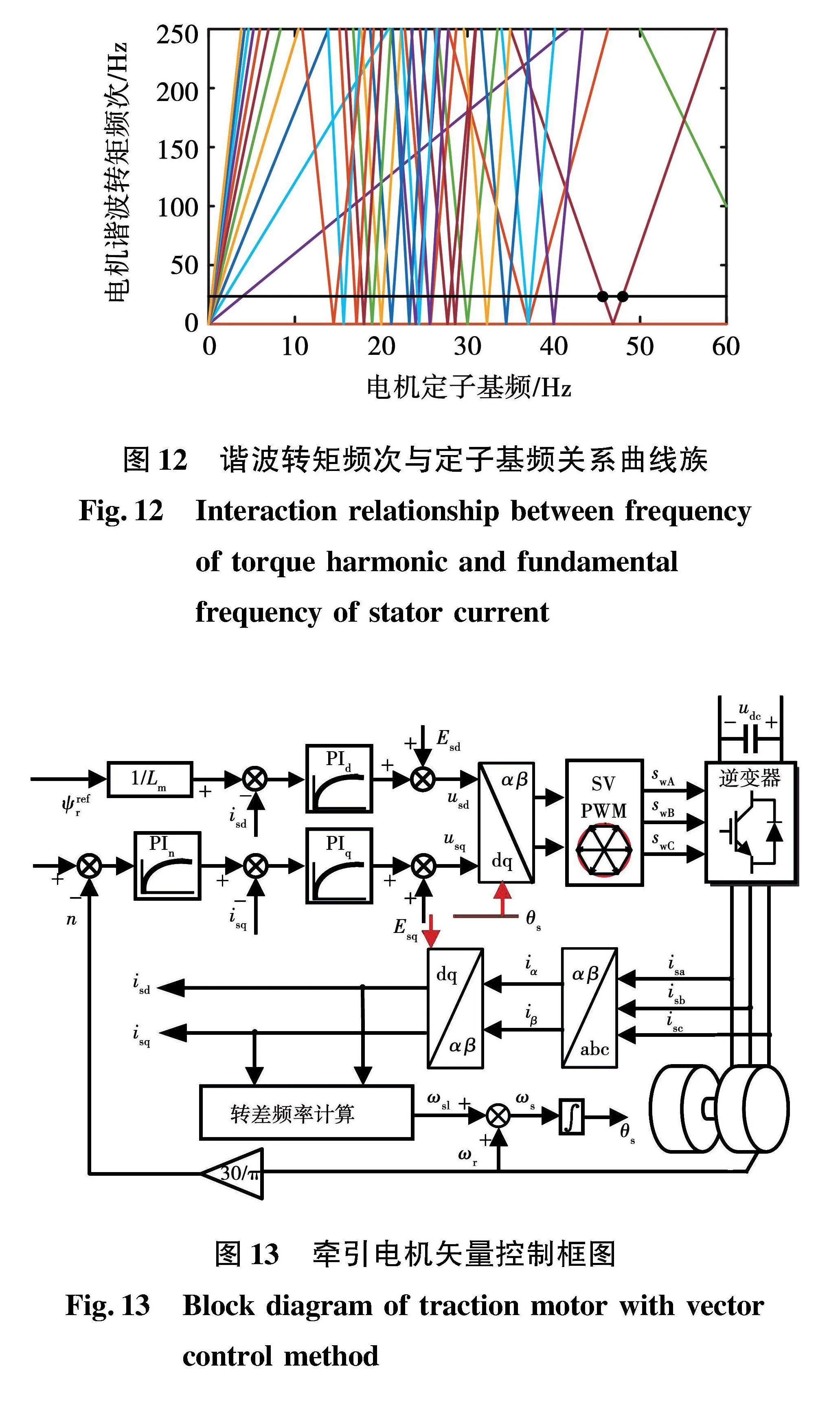
牽引電機采用和諧號CRH3牽引電機，參數如表2所示［19］。諧波轉矩的頻次由載波頻率及調制波頻率交互耦合產生，固定開關頻率，改變電機定子頻率即可獲得相應頻次的諧波轉矩。根據式（15），每一個x、y的取值組合確定一條定子基頻和諧波轉矩關系曲線，通過對x、y取不同組合可以構建出諧波轉矩頻率與電機基頻的關系曲線族，如圖12所示。由表1參數可得機械模型自然振蕩頻率為25 Hz，同頻電磁轉矩將引起機電耦合同頻振蕩，圖7中黑線的縱坐標代表機械自然振蕩頻率，與曲線族存在多個交點表示存在多個定子基頻會產生同頻諧波轉矩。x=2、y=42組合確定的曲線與自然振蕩頻率存在2個交點，代表存在2個定子頻率（47.02和48.21 Hz）會產生25 Hz的邊帶諧波轉矩，而且相比于更低基頻下的邊帶諧波，此時的反電勢Eg更大，邊帶效應更為顯著，因此可以選取47.02、48.21 Hz作為同頻振蕩速度點的驗證。采用三相交流異步電機，電機控制策略采用轉子磁鏈定向控制，調制方案采用異步調制策略。電機控制環節包括電流內環與轉速外環，分別采用PI控制器進行控制，為了減少PI控制器的運算負擔，加快系統的動態響應，在控制器輸出前向電壓基礎上，引入前饋指令電壓，其控制框圖如圖13所示。

根據轉子磁場定向的控制方式，在穩態下q軸磁鏈為0，由此得到轉差頻率和轉子磁鏈定向角分別為：

ωsl（t）=isq（t）LmTrψrd（t）；（18）

θs（t）=∫ωs（t）dt=∫（ωsl（t）+ωr（t））dt。（19）

式中：isq為電機定子q軸電流；Tr為電機轉子時間常數；ψrd為電機轉子磁鏈；ωs、ωsl、ωr分別為電機定子角頻率、轉差角頻率、電機轉子角速度。

同時，可以獲得穩態下的電磁轉矩方程為

Tm=npLmLrisq（t）ψrd（t）。（20）

由于控制對象是以CRH3牽引電機為核心的機電耦合系統，該系統具有結構復雜、功率大、危險程度高等特點，導致其測試設計困難。因此，搭建以實時仿真器和控制器為核心的硬件在環實驗平臺，對機電耦合振動機理進行驗證，半實物測試平臺控制結構圖如圖14所示。

由圖12可知，在固定的逆變器開關頻率下，電機基頻上升過程中，邊帶諧波頻率在進行機電耦合同頻振蕩時，共選取了2個頻率點，分別為47.02和48.21 Hz。而在電機閉環控制之中，需將其轉換成速度，考慮穩態下負載轉矩與電磁轉矩相等，可通過式（18）與式（19）得到負載轉矩產生的轉差角頻率，因此設定的速度需滿足：

nref=60（fs－fsl）np。（21）

在進行硬件在環測試時，選取負載TL=200 N·m，經計算同頻振蕩速度分別為1 410、1 446 r/min。以2種工況進行測試：1）升降速工況：設置負載轉矩TL=1 000 N·m，給定轉速nref=1 410 r/min→1 500 r/min→1 446 r/min。2）加減載工況：設置轉速nref=1 410 r/min，負載轉矩TL=1 000 N·m→1 500 N·m→1 200 N·m。為了反應機電耦合的嚴重程度，在2種工況條件下分別測試電機轉速與傳動軸扭矩。

1）升降速工況。

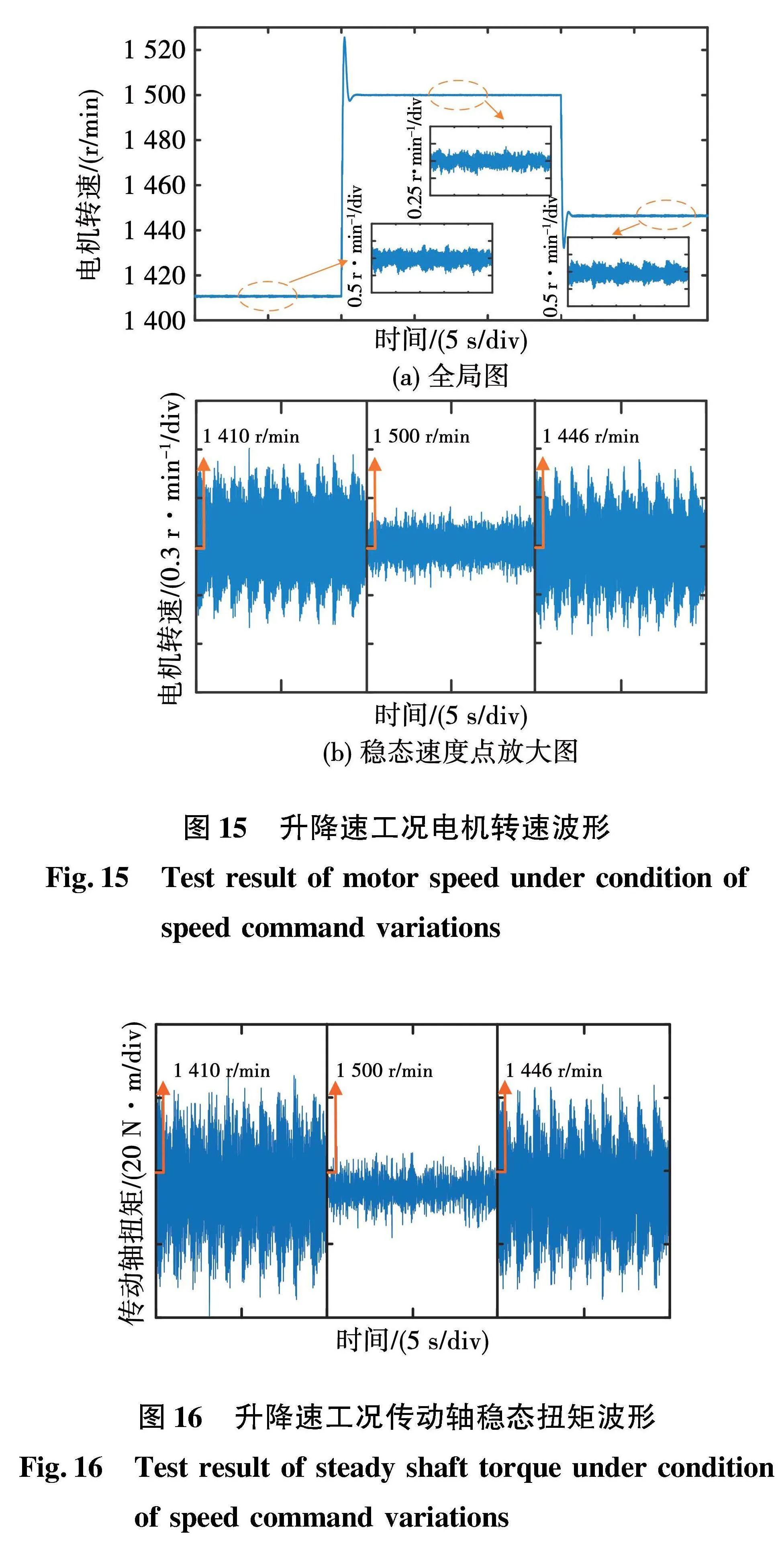
實驗結果如圖15與圖16所示，可知，在給定速度為1 500 r/min下，電機實際轉速及軸矩均比較平穩，而在同頻振蕩頻率下，由于諧波轉矩的幅值不同，電機實際轉速與軸矩均發生了不同程度的振蕩。系統如果長期處于扭振狀態下，將會導致軸系疲勞損傷，威脅列車的安全穩定運行。

2）加減載工況。

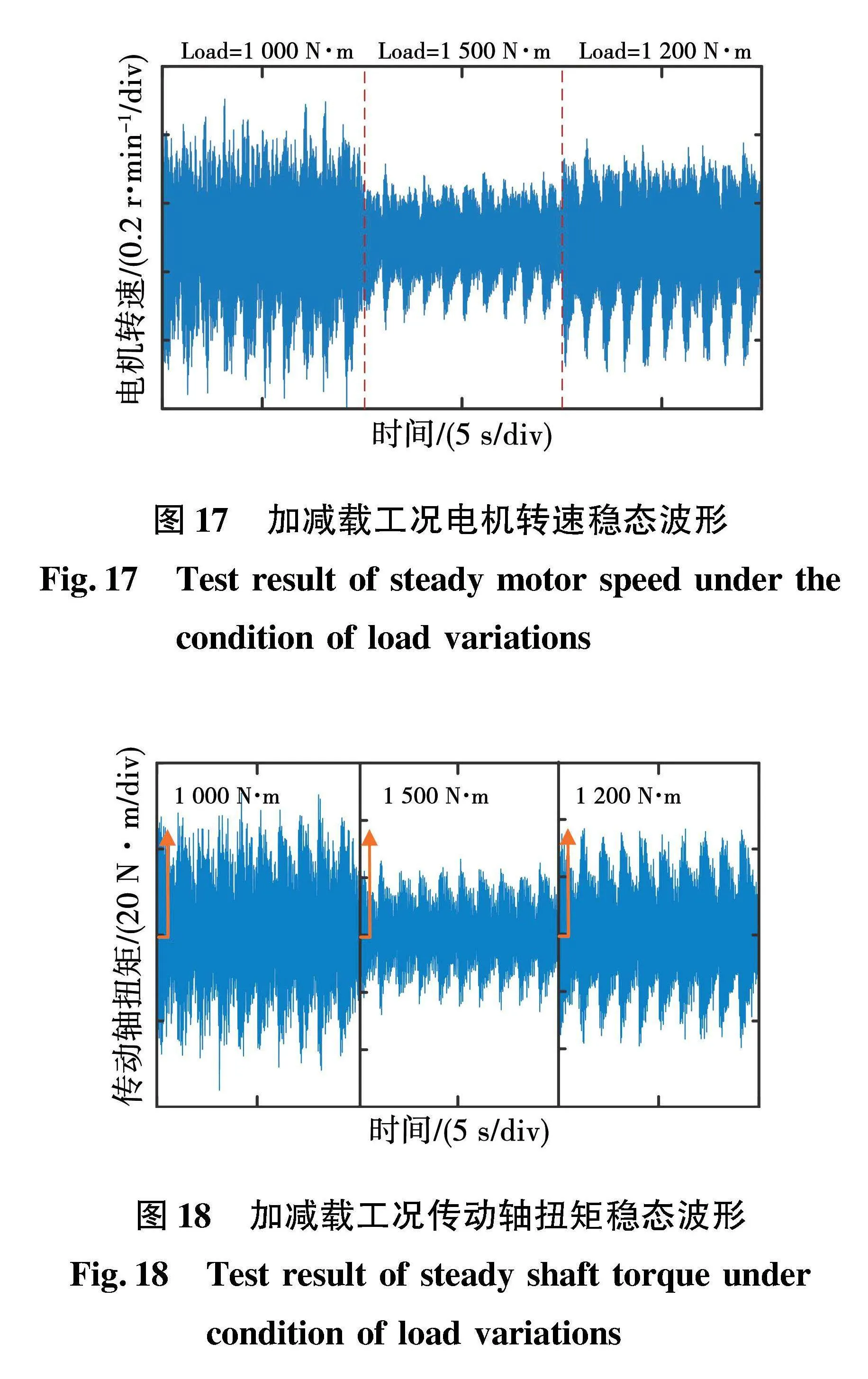
電機加減載階段，電機在1 410 r/min的同頻振蕩速度點時，都可以在穩態達到給定轉速，而當進行加減載操作時，會使電機的轉差頻率改變，進而使電機偏離同頻振蕩點，但由于轉差頻率很小，系統依舊接近同頻振蕩點。實驗結果如圖17和圖18所示，可以明顯看出，在加減載恢復至穩定轉速后，電機轉速及傳動軸扭矩的振蕩幅值均較同頻振蕩速度點有所減弱，但此時系統依舊有較大的振蕩。

5" 結" 論

本文針對牽引傳動系統機電耦合振動問題，對其振動機理進行了分析，得到如下結論：

1）分析了牽引傳動系統機電耦合扭振的誘因，在雙慣量系統模型基礎上復現了電機轉速閉環控制下不同速度點會發生同頻受迫振動。

2）分析了逆變器PWM調制輸出的電壓諧波特性和牽引電機輸出轉矩的諧波特性，并依據其伴生間諧波的分布規律，構建了諧波轉矩頻次與定子基頻的關系曲線族。

3）仿真和硬件在環測試表明，在變頻調速過程中，由于載波頻率和調制波頻率的交互耦合關系，邊帶諧波轉矩會在多個速度點產生相同頻次諧波轉矩，因此逆變器調制引起的間諧波是引發機電耦合同頻振動的來源之一。

參 考 文 獻：

［1］" 陳再剛， 劉禹清， 周子偉， 等. 軌道交通牽引動力傳動系統動力學研究綜述［J］. 交通運輸工程學報， 2021， 21（6）： 31.

CHEN Zaigang， LIU Yuqing， ZHOU Ziwei， et al. Review on dynamics research of rail transit traction power transmission system［J］. Journal of Traffic and Transportation Engineering， 2021， 21（6）： 31.

［2］" LU B， LIU Z， WANG X， et al. Influence of electric traction drive system harmonics and interharmonicson the vibration of key locomotive components［J］. IEEE Transactions on Vehicular Technology， 2023， 72（10）：12830.

［3］" KIA S H， HENAO H， CAPOLINO G A. Torsional vibration assessment using induction machine electromagnetic torque estimation［J］. IEEE Transactions on Industrial Electronics， 2009， 57（1）： 209.

［4］" WU X， CHI M， GAO H. Damage tolerances of a railway axle in the presence of wheel polygonalizations［J］. Engineering Failure Analysis， 2016，66： 44.

［5］" WU X， RAKHEJA S， QU S， et al. Dynamic responses of a high-speed railway car due to wheel polygonalisation［J］. Vehicle System Dynamics， 2018， 56（12）： 1817.

［6］" SMITH K S， RAN L. Torsional resonance risk management in islanded industrial power systems supplying large VFDs［J］. IEEE Transactions on Industry Applications， 2008， 44（6）：1841.

［7］" SONG-MANGUELLE J， SCHRDER S， GEYER T， et al. Prediction of mechanical shaft failures due to pulsating torques of variable-frequency drives［J］. IEEE Transactions on Industry Applications， 2010， 46（5）： 1979.

［8］" MAURI M， ROSSI M， BRUHA M. Generation of torsional excitation in a variable-speed-drive system［C］//2016 International Symposium on Power Electronics， Electrical Drives， Automation and Motion （SPEEDAM）， June 22-24， 2016， Capri， Italy. 2016： 516-521.

［9］" WANG Q， RAJASHEKARA K， JIA Y， et al. A real-time vibration suppression strategy in electric vehicles［J］. IEEE Transactions on Vehicular Technology， 2017， 66（9）： 7722.

［10］" 楊明， 郝亮， 徐殿國. 雙慣量彈性負載系統機械諧振機理分析及諧振特征快速辨識［J］.電機與控制學報，2016，20（4）：112.

YANG Ming， HAO Liang， XU Dianguo. Analysis of mechanical resonance mechanism and fast identification of resonance characteristic for 2-mass system with elastic load［J］. Electric Machines and Control， 2016， 20（4）： 112.

［11］" WINTERLING M W， TUINMAN E， DELEROI W. Attenuation of ripple torques in inverter supplied traction drives［C］//Seventh International Conference on Power Electronics and Variable Speed Drives， September 21-23， 1998， London， UK. 1998： 364-369.

［12］" WINTERLING M W， TUINMAN E， DELEROI W. Simulation of drive line dynamics of light-rail vehicles［C］//International Conference on Simulation 98， September 30-October 2，1998， York， UK. 1998： 79-84.

［13］" 趙心穎， 楊中平， 林飛， 等. 高速列車牽引傳動系統機電耦合振動及其影響因素分析［J］.鐵道學報，2019，41（10）：38.

ZHAO Xinying， YANG Zhongping， LIN Fei， et al. Study on electromechanical coupling vibration of traction drive system of high-speed train and its influence factor［J］. Journal of the China Railway Society， 2019， 41（10）： 38.

［14］" PHAM T H， WENDLING P F， SALON S J， et al. Transient finite element analysis for an induction motor with external circuit connections and electromechanical coupling［J］. IEEE Transactions on Energy Conversion， 1999， 14（4）： 1407.

［15］" 趙心穎， 林飛， 楊中平， 等. 高速列車牽引傳動系統機電耦合振動特性研究［J］. 鐵道學報， 2018， 40（9）： 40.

ZHAO Xinying， LIN fei， YANG Zhongping， et al. Study on mechanism and suppression of electromechanical coupling vibration in traction drive system of high-speed train［J］. Journal of the China Railway Society， 2018， 40（9）： 40.

［16］" BROCK S， UCZAK D， NOWOPOLSKI K， et al. Two approaches to speed control for multi-mass system with variable mechanical parameters［J］. IEEE Transactions on Industrial Electronics， 2016， 64（4）： 3338.

［17］" YANG S M， WANG S C. The detection of resonance frequency in motion control systems［J］. IEEE Transactions on Industry Applications， 2014， 50（5）： 3423.

［18］" HOLMES D G， MCGRATH B P. Opportunities for harmonic cancellation with carrier-based PWM for a two-level and multilevel cascaded inverters［J］. IEEE Transactions on Industry Application， 2001， 37（2）： 574.

［19］" 汪斌. 列車牽引傳動系統性能分析和仿真技術研究［D］.杭州： 浙江大學， 2013.

（編輯：邱赫男）