核心素養視域下混合式教學在高中物理教學中的應用

混合式教學是綜合運用不同的學習理論、技術和手段以及不同的應用方式來開展教學的一種方式，可以將線上教學與傳統課堂教學相結合，發揮線上教學的優勢，有效彌補傳統課堂教學存在的不足，引導學生展開深度學習。

一、整合資源，制訂提綱

在高中物理課堂中應用混合式教學時，教師可以按照課程的類型設計教案，如復習課、實驗探究課以及概念課等，再借助網絡課程資源整合物理相關資料，圍繞教材內容、教輔資料等制作有趣味性的教學視頻、制訂課前學習提綱、優化課前檢測習題等。在教學視頻制作中，教師應充分利用學習平臺，為學生展示多維度、多角度的物理實驗過程，以此提升學生的科學素養。

●案例一：以豎直方向的圓周運動為例

教學重點：在軌道模型當中，實驗小球在無法達到最高點時的分析相對較難，需要融合斜拋運動和牛頓第二定律。

教學重點：對繩和桿兩種模型的特點進行理解。

教學過程：

教師展示現實生活中的過山車圓周運動圖片。

師：過山車是一項充滿刺激的游戲，大家體驗過嗎？

生：小時候在公園里坐過。

師：其實過山車的運動包含許多物理學原理，大家說一說。

生：能量守恒、加速度和力。

師：在回環的頂部，乘客完全倒轉過來，為什么不會掉下來呢？讓我們通過下面的例子分析其中的物理原理。請看圖1。

圖1 豎直平面內軌道模型圖

師：該圖形為一個光滑的圓軌道圖形，此時給小球一個運動的速度，已知圓環半徑為R，重力加速度為g。請問：

（1）要想小球順利通過圓環最高點，小球在最低點的最小初速度為多少？

（2）在不離開圓環的情況下，小球在最低點的初始速度需要何種條件？

（3）小球脫離圓環的情況下，小球脫離的條件和脫離位置分別是什么？

（設計意圖：利用上述三個小問題打開學生的思維，同時引導學生對問題進行針對性分析和討論。）

生1：想要讓小球順利通過最高點，那么小球的速度條件應為mg≤，最高點的速度為v≥，從而在最低到最高兩個點的運動過程，按照動能定理可表示為：mv02=2mgR+mv2，進而將公式v≥帶入公式mv02=2mgR+mv當中，可得到初始速度條件，表示為：v0≥。

生2：想要解決第二個問題，就需要讓小球順利通過最高點，或者小球在最低點到處做運動，那么按照上一位同學的解釋，第一個問題就可以解決；而第二種情況下，小球的速度應當為0，所以按照動能定理，可知mv02=mgR，也就是說v0≤，進而想要小球不脫離軌道，那么最低點的速度就需要滿足v0≤或v0≥兩種條件。

（設計意圖：在分享成果的過程中，培養學生的科學探究能力與邏輯推理能力，同時能按照學生的探究成果，掌握學生的學習和思考情況。）

二、上傳資料，獨立學習

混合式教學要求學生能夠獨立且主動地參與到學習活動中，利用在線學習方式學習，這樣的學習模式需要學生具備一定自我管控能力和約束力。教師借助信息技術將相關學習資料上傳到學生學習平臺，學生根據教師上傳的資料自主學習，初步認識本節課的物理知識，高效完成學習計劃。當教師講解物理知識時，學生要及時做好知識記錄，標注自己不懂的物理問題，通過學習平臺和教師上傳的視頻資料，在初步了解和掌握物理知識后，采取循序漸進的方法學習物理知識。教師則可以借助信息技術及時掌握學生的學習情況，做好教學安排，并在學習平臺上設定相應的物理問題，實時觀察和了解學生的自主學習狀態，掌握學生的學習難點，有針對性地優化教學設計和物理核心素養的培養，實現提高教學質量的目標。

●案例二：以完全非彈性碰撞課程為例

教學重點：學會利用動量和能量處理碰撞問題。

教學難點：在同種場景或條件下，對不同運動過程的分析。

教學過程：

教師將本次課程的教學引導內容以練習的形式上傳至線上學習系統當中，利用圖像觀察的方式，幫助學生構建課程初始知識結構，之后結合圖片提出對應的思考問題，要求學生完成思考內容的填寫，教師提出問題：

（1）在牛頓小擺球實驗當中，為什么只需要對首尾其中一個球施加動能，另一端小球就會彈起？

（2）之前學習的三種碰撞類型分別為什么？

（3）不同類型的碰撞條件分別為什么？

生1：當兩個金屬球碰撞時，就會發生彈性碰撞。

生2：有完全彈性碰撞、非完全彈性碰撞、完全非彈性碰撞三種。

生3：三種碰撞碰前后需要滿足動量守恒的條件，其中完全彈性碰撞，前后能量不變；非完全彈性碰撞，前后能量出現減少；完全非彈性碰撞，前后能量減少，并且減少量為最大。

（設計意圖：將生活中的物理現象融入課程教學中，加深學生對物理與生活息息相關的意識。）

在學生完成該部分內容后，教師引導學生發現問題，并建立相應模型，以及在課件當中逐條展示出模型的規律，如圖2所示。

如圖2所示，在水平光滑的地面上A、B兩個物體之間用一個彈簧進行連接，已知物體A的質量為G，物體B的質量為2G。此時物體A位于墻邊，對物體B施加一個F的力，使其逐漸向物體A靠近，此時彈簧的彈性勢能表示為：Ep=8Gg，之后將F撤掉，請問：

（1）在施加F力過程中，物體A和B之間形成系統機械能和動量是否守恒？

（2）撤掉力F后，物體A和B之間形成系統動量與機械能是否守恒？

（3）撤掉力F后，物體A離開墻面，物體A和B之間形成系統動量和機械能是否守恒？

生1：物體A和B之間形成系統機械能不守恒，動量也不守恒。

生2：撤掉力F后，物體A和B之間形成系統動量守恒，動量不守恒。

生3：撤掉力F后，物體A離開墻面，物體A和B之間形成系統動量和機械能守恒。

（設計意圖：提供模型演練的方式，使學生可以輕松理解物理概念。）

三、線下教學，解答難題

利用信息技術回收學生學習難題清單，結合學生對物理知識產生的疑問，在線下教學過程中強調重點，幫助學生解決難題。在答疑解惑的過程中，教師分類講解相關知識，當學生領悟物理知識點以后，教師詳細講解課前習題，深化學生對物理知識的記憶和領悟。

●案例三：以實踐物理實驗——向心力的計算為例

首先，設定實驗背景。在游樂園當中有飛椅的娛樂項目，將座椅用鋼索固定在一個較大的轉盤上，之后啟動轉盤，致使轉盤進行圓周運動，此時座椅出現轉動并超過轉盤的區域，那么此時座椅受到的向心力該如何計算。

其次，制作實驗器械。利用學校現有的呼啦圈，將其作為轉盤，再在呼啦圈上系上一重物，將其作為座椅，之后教師在黑牌上畫出處理后的抽象示意圖，如圖3所示。

圖3 飛椅抽象處理示意圖

由圖3可知，d為呼啦圈的半徑，F為轉動的力，轉動方向為逆時針，θ為重物與垂直方向的夾角，進而不考慮重物自身質量的條件下，直接計算出座椅的轉動過程所呈現的夾角。

最后，分析效果。通過分析上述已知條件，可以準確知道座椅在轉動過程中，將角速度設定為α，將重物與垂直方向的角設定為θ，那么轉動過程中與轉軸之間的距離即為D，轉動過程中的向心力計算表示為：F=mg tanθ=mDα2，經過計算后得出α，表示為：α=。

（設計意圖：運用物理實驗引導學生思考，使學生可以將物理與生活聯系起來）。

四、優化習題，鞏固知識

進入知識內化階段，教師應結合學生的學習現狀和教學重難點，運用互聯網技術資源豐富、信息多元化的優勢，搜集專業的物理習題，并同步到學習平臺上，通過循序漸進的知識練習讓學生鞏固物理知識。學生完成學習平臺上的習題后，系統可以將最終成績反饋到教師平臺，這樣教師就能及時掌握學生的學習情況，從而適當調整教學計劃，通過有針對性的教學方式強化學生的物理意識。

●案例四：以豎直方向的圓周運動習題講解為例

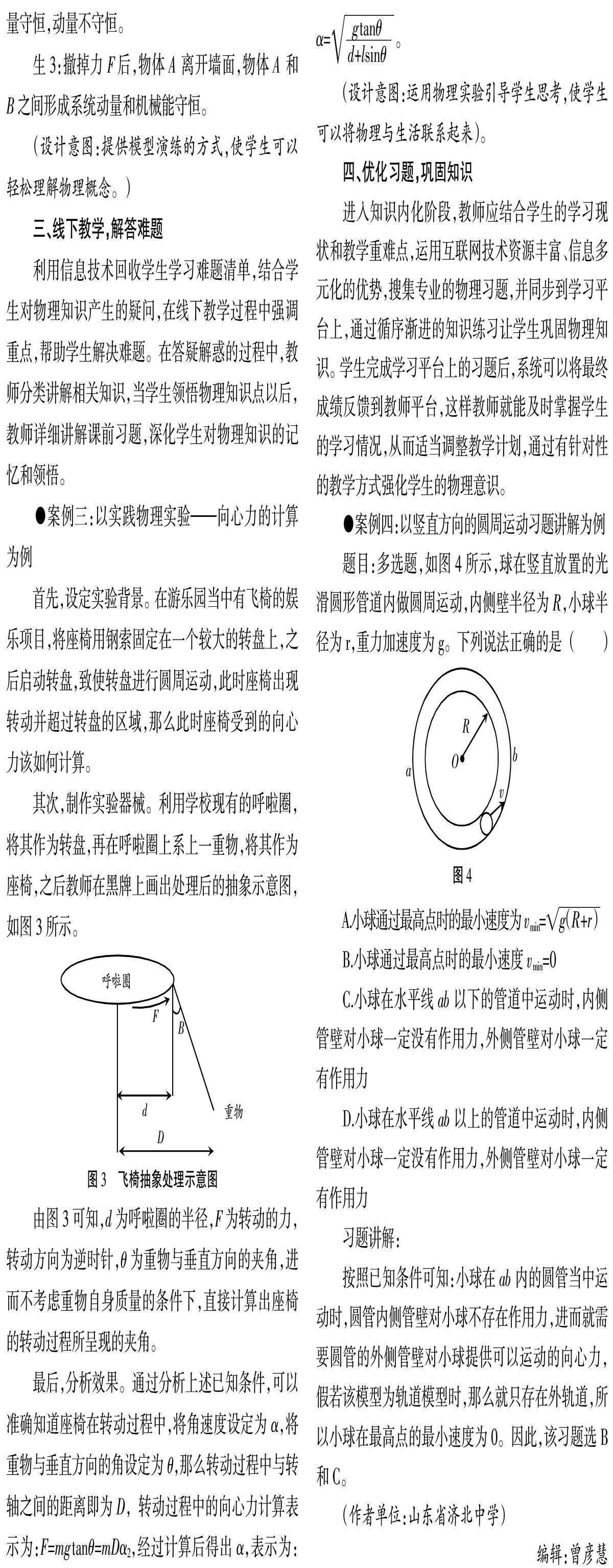
題目：多選題，如圖4所示，球在豎直放置的光滑圓形管道內做圓周運動，內側壁半徑為R，小球半徑為r，重力加速度為g。下列說法正確的是（ ?）

A.小球通過最高點時的最小速度為vmin=

B.小球通過最高點時的最小速度vmin=0

C.小球在水平線ab以下的管道中運動時，內側管壁對小球一定沒有作用力，外側管壁對小球一定有作用力

D.小球在水平線ab以上的管道中運動時，內側管壁對小球一定沒有作用力，外側管壁對小球一定有作用力

習題講解：

按照已知條件可知：小球在ab內的圓管當中運動時，圓管內側管壁對小球不存在作用力，進而就需要圓管的外側管壁對小球提供可以運動的向心力，假若該模型為軌道模型時，那么就只存在外軌道，所以小球在最高點的最小速度為0。因此，該習題選B和C。

（作者單位：山東省濟北中學）

編輯：曾彥慧

作者簡介：安波（1982—），男，漢族，山東濟南人，本科，中學一級教師，研究方向：高中物理。