雙周期參數系統的受迫振動響應*

顧京君 童彤 黃迪山

(1.南通振康機械有限公司,南通 226153)

(2.上海大學 機電工程與自動化學院,上海 200444)

引言

諧波減速器廣泛應用于各種機器人關節,它由柔輪、剛輪、波發生器三大基本構件組成.波發生器鑲套在柔輪內圈,柔輪齒與剛輪齒進行內嚙合,柔輪齒數比剛輪齒數少,因此,它是一個少齒差傳動機構.其中,波發生器由橢圓凸輪外套柔性滾動軸承組成,基本結構如圖1所示.

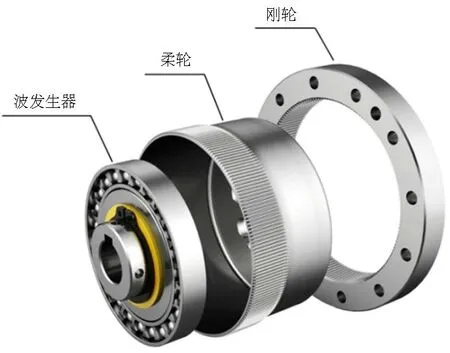
圖1 單剛輪諧波減速器基本結構Fig.1 Basic structure of single rigid wheel harmonic reducer

在制造過程中,如果柔輪齒與剛輪齒引入了周節累積誤差,則諧波減速器在動力傳遞中將出現雙周期時變扭剛度波動,形成雙周期參數振動問題.

關于單自由度參數系統振動,學者王建軍等[1,2]利用Sylvester理論和Fourier 級數給出了自由和受迫振動響應的級數解;Sinha[3]基于雪比多夫多項式,推出逼近級數解;Ivana Kovacic[4]回顧了幾種典型參數激勵下的穩定性區域求解.近幾年,利用組合頻率三角級數法[5,6]應用于多自由度參數振動分析,確定了自由與受迫振動響應的解析逼近.而大多數文獻研究內容在基于Floquet理論上討論參數振動穩定性問題[7-11].但是,對于雙周期參數振動的響應預測問題,仍然需深入探討.

本文針對電機、諧波減速器和慣量負載傳動問題,建立雙周期參數振動方程,引入基于組合頻率的二重三角級數,對其響應進行級數逼近解研究.

1 動力學建模與二重三角級數逼近

在電機、諧波減速器和慣量負載傳動中,考慮雙周期時變扭剛度波動,建立雙周期……