例說圖形的平移

陳瓊

抓住圖形平移的特點，掌握圖 形平移的規律，有利于同學們提高 解題能力.

人教版數學教科書七年級下冊第31頁第6題的內容為：

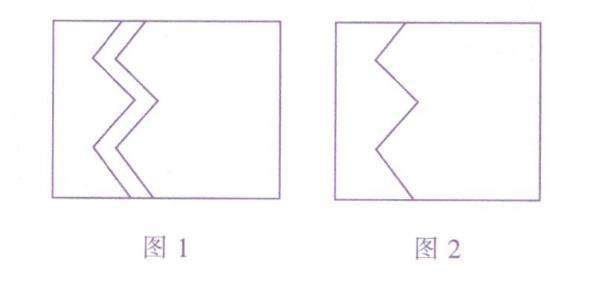
如圖1，在一塊長為am，寬為bm的長方形草地上有一條彎曲的小路，小路的左邊 線向右平移1m就是它的右邊線.求這塊草 地的綠地面積.

解決此題較簡單，將圖1中小路右邊 的圖形向左平移1m，則圖1中的小路左右 邊線重合，如圖2.比較圖1和圖2，可以發現 它們長相差1m，寬均為bm，于是得到這塊 草地的綠地面積為（a-1）bm?.

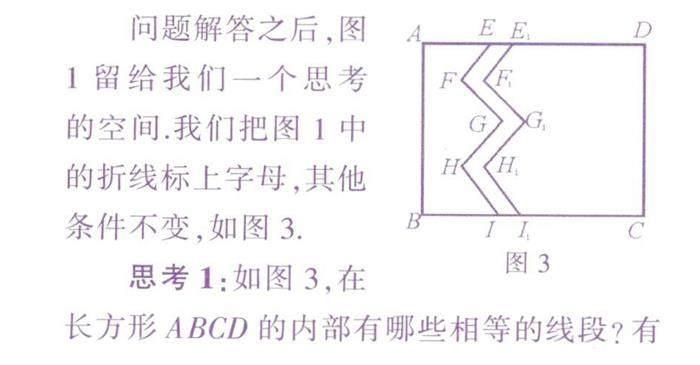
問題解答之后，圖 1留給我們一個思考 的空間.我們把圖1中 的折線標上字母，其他 條件不變，如圖3.

思考1：如圖3，在長方形ABCD的內部有哪些相等的線段？有哪些相等的角？

分析：根據平移的性質，容易得到EF=EF1，FG=F1G1，GH=G1H1，HI = HI1LF= ∠F1，∠G=∠G1，∠H=∠H1。

思考2：如果連接FF1，GG1，HH1，那么FF1，GG1，HH1之間有何數量、位置關系？

分析：點F與F1，點G與G1，點H與H1 分別是平移過程中的對應點，根據平移的性質， 容易得到FF1=GG1=HH1，并且FF1//GG1//HH1.

思考3：如圖4，∠AEF，萊弗格，∠FGH，∠GHI，∠HIB之間有何數量關系？

分析：分別過點F，g，H作FP//AE，GQAE、HW//AE、而AE//BI，根據平行線的性質，得到：AE//FP/GQ//HW//BI.所以AEF=LEFP， LFGQ= ∠ PFG， ∠QGH= ∠GHW，∠HIB=∠IHW.以上四式相加，得到：∠AEF + ∠FGQ+ ∠QGH + ∠HIB= ∠EFP+∠PFG+∠GHW+∠IHW.故∠AEF+∠FGH+∠HIB= ∠EFG+ ∠GHI.

需要說明的是，可以將圖4 簡化為一個基本模型，如圖5， 類似得出一個有用的結論：如 圖5，如果AB//CD，那么人∠ABE+∠CDE=∠BED。

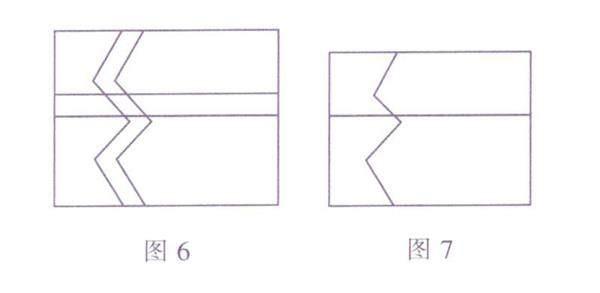
變式1：在一塊長為am，寬為bm的長方形草地上有一條彎曲的小路，小路的左邊 線向右平移1m就是它的右邊線，再修建一 條平行于長邊，且寬為1m的小路，如圖6， 你能求出這塊草地的綠地面積嗎？

分析：能.先將圖6中彎曲小路右邊的 圖形向左平移1m，則小路的左右邊線重合， 再將水平小路上方的圖形向下平移1m，最 后得到一個長為（a-1）m，寬為（b-1）m的長 方形，如圖7.可得到這塊草地的綠地面積為（a-1）（b-1）m2.

思考：變式1中，水平小路的邊線與長 方形的長邊平行，如果水平小路的邊線與長 方形的長邊不平行，路口寬為1m，如圖8， 還能用上面的方法得出相同的結果嗎？

分析：如果水平小路的邊線與長方形 的長邊不平行，則彎曲小路與水平小路重疊 部分的面積不一定是1m?，故不能用上面的 方法得出相同的結果.借助于幾何畫板，按 照上面的平移方式，會發現在本圖中的綠地 面積小于（a-1）（b-1）m2.

上述質疑釋惑的過程給我們一個啟示： 用整體思想方法解題時，對于條件或圖形結 構類似，但本質有所不同的問題，要仔細分 析，切記不要用原有的經驗想當然地生搬硬套，謹防出錯.

變式2：在長為am，寬為bm的長方形 草地上，有一些小路，小路的邊線與長方形的 邊平行或垂直，小路路口寬為1m，如圖9.你能求出這塊草地的綠地面積嗎？

分析：先將圖中小路右邊的圖形向左 平移1m，再將小路上方的圖形向下平移 1m，得到一個長為（a-1）m，寬為（b-1）m的 長方形.于是得到這塊草地的綠地面積為（a-1）（B- 1）m2。

思考：變式2中，如果小路的邊線與長 方形的邊不平行或不垂直，小路路口寬仍為 1m，如圖10，還能用上面的方法得出相同的 結果嗎？

分析：如果小路的邊線與長方形的邊 不平行或不垂直，則圖中的不同方向的小路 重疊部分有兩塊，其面積均不一定是1m?， 故不能用上面的方法得出相同的結果.借助 于幾何畫板，按照上面的平移方式，會發現 本圖中的綠地面積大于（a-1）（b-1）m?.

總之，解決圖形平移中的計算問題時， 一定要把握圖形平移過程中相關線段、角以 及面積的不變性規律，并且要善于區分相似 圖形結構中的不同特征，以達到正確解決問 題的目的.