2023年全國高考乙卷理綜第25題的評析與思考

摘 要：2023年全國乙卷理綜第25題為物理壓軸題，綜合性強、運動過程復雜、難度大，突出體現了對學生必備知識、關鍵能力和綜合素質的考查.本文從命題意圖、試題釋疑、試題解評、教學思考等方面進行探討.

關鍵詞：彈性碰撞；試題評析；教學思考

中圖分類號：G632?? 文獻標識碼：A?? 文章編號：1008-0333（2024）01-0100-03

收稿日期：2023-10-05

作者簡介：鄧偉（1976.1-），男，中學高級教師，從事試題與教學實踐研究.

2023年高考全國理綜乙卷物理試題全面落實教育立德樹人的根本任務.加強教考銜接，遵循課程標準，依托中國高考評價體系，注重深化物理基礎；增強探究性，突出科學思維考查和科學素養考查，注重物理方法的培養，引導教學注重作業題、訓練題減量提質，減少“重復、機械刷題”，促使教學把教材內容講全講透，提升課堂效果，形成學生必備知識與關鍵能力.而高考壓軸題作為一份試卷的精華所在，也是高考命題的風向標，最能體現高考的命題意圖和思想.試題分析就是一線教師與命題者的間接“對話”，應充分理解考題的設計意圖，從而對高中物理教學發揮更加明確的導向作用.

1 原題重現

（2023年全國乙卷理綜第25題）如圖1所示，一豎直固定的長直圓管內有一質量為M的靜止薄圓盤，圓盤與管的上端口距離為l，圓管長度為20l.一質量為m=13M的小球從管的上端口由靜止下落，并撞在圓盤中心，圓盤向下滑動，所受滑動摩擦力與其所受重力大小相等.小球在管內運動時與管壁不接觸，圓盤始終水平，小球與圓盤發生的碰撞均為彈性碰撞且碰撞時間極短.不計空氣阻力，重力加速度大小為g.求：

（1）第一次碰撞后瞬間小球和圓盤的速度大小；

（2）在第一次碰撞到第二次碰撞之間，小球與圓盤間的最遠距離；

（3）圓盤在管內運動過程中，小球與圓盤碰撞的次數.

2 試題評析

2.1 命題意圖

落實物理學科核心素養是2023年全國乙卷理綜第25題命題的最大亮點，物理觀念和科學思維是物理學科核心素養的重要組成部分.培養學生的物理觀念，決定著學生對物理知識理解的深入度和應用的靈活性，對學生終生的學習和發展具有重要作用；培養學生的科學思維，讓學生能夠對模型建構、科學推理、科學論證、質疑創新等要素和科學思維方法有機整合.本題直觀考查了彈性碰撞相關知識，深入考查了物理觀念中的物質觀、運動觀、能量觀和科學思維中的模型建構、科學推理等核心素養的重要方面.在熟悉的情景中，注重考查了學生是否具有獨立思考、分析問題和靈活解決問題的科學思維能力.引導物理課堂應跳出題海戰術，樹立學生正確的思維方式，提高學生物理學科核心素養，為學生的終生發展奠基.

2.2 試題釋疑

本題的疑點是第（3）問.小球反復地追擊圓盤并發生彈性碰撞，體現在運動過程復雜、多次彈性碰撞的計算難度大，用常規的分段分析的方法解答，耗時多，因此對思維方法、規律把握、解題方法和計算要求較高.因此，突破疑點應抓以下幾個方面：第一，除碰撞瞬間，小球做加速度為g的勻變速直線運動，圓盤做對應階段的勻速運動；第二，受限條件是管的總長度20l，但注意圓盤初始位置離上管口為l，可以通過圓盤向下運動的位移與這一條件建立聯系；第三，圓盤運動中受力平衡，小球在管中下降減少的重力勢能轉化為小球、圓盤的動能；第四，每相鄰兩次碰撞的時間相同，每次碰撞前后瞬間小球、圓盤的相對速度大小相等，方向相反，即深度掌握和熟練應用彈性碰撞規律.

2.3 試題解析

分析 第（1）問體現了基礎性，考查了勻變速直線運動（自由落體）和典型碰撞模型彈性碰撞，突顯物理學科核心素養中的運動觀與模型建構能力.本問物理情景、運動規律學生較熟悉，解答方法較多，比較容易.學生存在的問題是對“一動一靜”式彈性碰撞的方程不會解或沒有記住碰撞后的速度關系.

（2）類比成追擊相遇問題，利用v-t圖像求解.

分析 第（2）問在第（1）的基礎上，由單一物體的運動變成兩個物體的運動，除了運動與碰撞外，還增加圓盤的受力平衡，難度加大.結合（1）問碰撞后的速度和圓盤的受力情況，也較為容易分析出小球和圓盤的運動情況.解答的方法較多，應用v-t圖像求解簡便、省時.學生存在的問題是第（1）問的速度沒有算出，無法進行后續分析.

（3）本問是本題的分水嶺，采用多種方法求解.

解法1 常規解法，分段分析

解法2 歸納法與能量的結合

解法3 利用v-t圖像

分析 第（3）問綜合難度大，小球反復地追擊圓盤并發生彈性碰撞，運動過程復雜、多次彈性碰撞的計算難度大.這就要求學生真正理解彈性碰撞的特點，同時全局把握小球、圓盤的運動規律、能量轉化情況，從而選擇合適的解題方法.解法1是大多數學生都能想到的，但解答過程復雜、耗時多，不能完整解答；解法2從整體上分析得出碰撞后瞬間小球、圓盤的速度“通項式”和能量轉化關系，解答較為容易，但學生不易想到；解法3利用v-t圖像，解法簡潔直觀、思路清晰、運算簡單，解答效率更高，且運動學圖像也是學生較熟悉的，但不少學生不習慣利用圖像輔助解題［1］.學生存在的問題是本問綜合性強、難度大，物理過程分析不清，甚至較多學生無時間分析而放棄.

3 教學思考

3.1 解題思維障礙分析

物理教學過程是引導學生進行觀察、分析、解決問題的過程.然而，在教學過程中，時有學生反映如下問題：（1）課堂上講的內容能夠理解，但是再次碰上相同或者相似模型時，卻感到熟悉又無奈；（2）刷了很多習題，但是解題過程依然處處碰壁；（3）解題過程中認為思路是對的，結果發現解答不下去，半途而廢.以上反映在多次彈性碰撞類問題中更為突出.說明學生并沒有從學習活動中獲取解決問題的關鍵能力，主要表現在套用模型導致解題思路固化的思維障礙. 在學習構建模型過程中，很多學生選擇把模型記住，在解題過程中直接把記憶中的模型和對應的規律進行復述.而實際問題的情境是多變的，所需要構建的模型也是相應變化的，應用的規律、解題的方法也隨之而變，因此學生的思維在此處脫節，造成了思維上的障礙.這說明學生對模型的分析不夠深入，對規律不能類化、遷移，從而影響解題.

3.2 思維障礙突破策略

隨著新高考的不斷深化，必須正視高考對教學的引導功能.如果教師還只停留在教給學生知識，而不注重學生分析問題和解決問題能力的提升、解答方法的引導，稍為靈活的試題或壓軸題就會成為多數學生的分水嶺.在2023年全國乙卷理綜第25題第（3）問中，學生能夠感受到彈性碰撞模型很熟悉，想法可能也很多，但卻無法有效解決問題，熟悉的模型變得不再熟悉［2］.

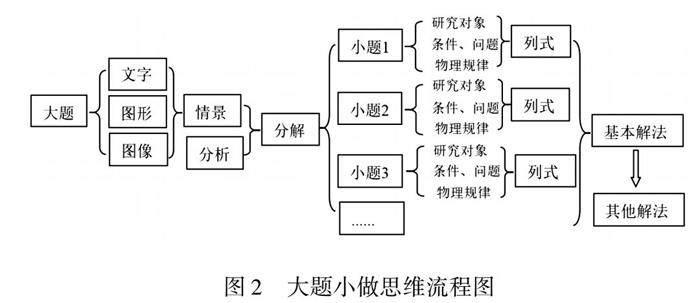
因此，物理學科的規律不是套路，解題過程更不能生搬硬套，而是要把握解決問題的規律.其中模型、條件可以根據實際情境千變萬化，但是解題的規律卻是相對穩定的，分析透物理規律，才能選擇靈活的解法.如何利用學科關鍵能力解決物理問題是教學中的重要目標，可以把每個綜合問題（大題）都可分解為多個小問題（小題），即采用“大題小做”的問題解決模式（如圖2），對問題的分析將更具有可行性.

以本題為例.此問涉及多對象、多階段、多規律的復雜運動，學生看完問題后思維容易混亂.若采用大題小做的問題解決模式，本題的思路就比較清晰了.如小題1，小球做自由落體運動，列勻變速直線運動方程；小題2，小球與圓盤發生彈性碰撞，列動量守恒和動能守恒方程；小題3，由小題2的結果可得小球做豎直上拋運動，圓盤受力平衡做勻速直線運動，類似追擊相遇問題，小球先向上減速然后向下加速追上圓盤并發生第二次碰撞，列小球、圓盤位移相等方程、勻變速直線運動速度關系，彈性碰撞動量守恒、動能守恒方程；小題4，小球第二次碰撞后瞬間的速度為0，做自由落體運動，圓盤以第二次碰撞后瞬間的速度做向下勻速直線運動.小球追上圓盤發生第三次彈性碰撞，列式與小題3相似；再續分小題，分析思路與小題3、4類似，這就是基本解法.通過基本解法中碰撞前后小球、圓盤的速度關系分析，能量情況分析，可以靈活選擇其他解法.

4 結束語

高考試題是經過命題專家深思熟慮的結果，經典模型［3］不按“套路”出牌，常考常新是高考試題的亮點.通過對2023年全國高考乙卷理綜第25題分析，可以看出試題以經典的彈性碰撞模型為基礎，通過受力分析、運動情況分析、能量角度的思考，考查綜合分析能力、情景類比遷移能力、計算能力、識圖作圖能力等，充分落實物理學科核心素養中的物理觀念和科學思維中的運動觀、能量觀、模型建構等方面能力要求.雖然本題物理模型、情景熟悉，但是卻對學生必備知識、關鍵能力的要求很高，需要學生能夠靈活分析，巧妙解答.這就要求教師在課堂教學中既要立足于基礎，即立足于物理的基本概念、基本規律、基本方法和基本技能，又要重視思維方法的引導、拓展，解題方法的訓練與提升.高考注重能力的考查，實際上是考查學生對基本知識、基本技能的理解、掌握和結合實際的靈活運用.對待基礎知識，一應理解和應用，二應注重歸納與建構，三應綜合與遷移，落實學科關鍵能力的培養.

參考文獻：

［1］ 張其林.巧用數形結合 助力物理解題［J］.中學物理，2022（1）：51-52.

［2］ 曹芳.深耕教材 強化主干 提升素養［J］.物理教學，2022（9）：57-59.

［3］ 李恒林.抓住題眼巧建模 科學推理真收獲［J］.物理教師，2022（11）：87-89.

［責任編輯：李 璟］