基于公平-經濟-減排的多目標水資源配置模型

劉稀琛 張曉東

文章編號：1671-3559（2024）03-0274-06DOI：10.13349/j.cnki.jdxbn.20240328.001

摘要： 為了解決水資源分配中的公平、 經濟和可持續問題，提出一種多目標水資源優化配置模型，在提高經濟效益的同時減小區域總污水排放量；以青海省龍羊峽水庫為研究對象，分析研究區域的水資源狀況，以區域系統經濟效益、 各用水分區的配水滿意度最大化和區域污水排放總量最小化為目標，建立多目標水資源優化配置模型探究區域的最佳配水方案；根據區域實際情況設定較高、 較低2個不同可用水量水平，探究在用水分區不同最低配水滿意度下配水方案的變化。結果表明：多目標水資源優化配置模型生成的配水方案經濟效益最高可提升約2.57×1010元，污水排放量最高可減少約1.8×107 t；該模型在提高經濟效益和分配公平性的同時促進污水減排，實現減排和經濟效益之間的權衡，為區域不同情景下的水資源配置和規劃提供經濟、 有效的決策支持。

關鍵詞： 水資源優化配置； 多目標線性規劃； 配水滿意度； 經濟效益； 污水排放

中圖分類號： TV213.4

文獻標志碼： A

開放科學識別碼（OSID碼）：

A Multi-objective Water Resources Allocation Model Based on

Equity-Economy-Emission Reduction

LIU Xichen， ZHANG Xiaodong

（School of Environmental Science and Engineering， Shandong University， Qingdao 266237， Shandong， China）

Abstract： To further address the issues of equity， economy， and sustainability in water resource allocation， a multi-objective water resource optimization allocation model was proposed， which aimed to enhance economic benefits while reducing the total regional wastewater discharge. Taking the Longyangxia Reservoir in Qinghai Province as the research subject， the water resource conditions of the research area were analyzed， and a multi-objective water resource optimization allocation model with the goals of maximizing regional system economic benefits， maximizing the satisfaction of water distribution in each water-use sector， and minimizing the total regional wastewater discharge was found to explore the optimal water distribution scheme for the region. Based on the actual regional conditions， two different levels of higher and lower available water were set to investigate the changes in water distribution schemes under different minimum satisfaction levels of water-use sectors. The results show that the water distribution schemes generated by the multi-objective water resource optimization allocation model can increase the economic benefits by up to approximately 2.57×1010 CNY， and reduce wastewater discharge by up to approximately 1.8×107 t. The model promotes wastewater reduction while improving economic benefits and distribution fairness， achieving a balance betweenemissionreductionandeconomicbenefits， and can provide economic and effective decision support for water resource allocation and planning under different regional scenarios.

Keywords： optimal allocation of water resource; multi-objective linear programming; satisfaction; economic benefit; sewage emission

收稿日期： 2023-01-09????????? 網絡首發時間：2024-03-29T12：22：10

基金項目： 國家重點研發計劃項目（2022YFC3204400）

第一作者簡介： 劉稀琛（1998—），女，山東濟南人。碩士研究生，研究方向為流域水資源管理。E-mail： lxc2020@mail.sdu.edu.cn。

通信作者簡介： 張曉東（1978—），男，河南周口人。教授，博士，博士生導師，研究方向為流域水資源和環境管理。E-mail： xdzhang@sdu.edu.cn。

網絡首發地址： https：//link.cnki.net/urlid/37.1378.N.20240328.1626.002

近幾十年來，隨著全球城市化和人口劇增，全社會用水量急劇增加。在水資源匱乏的地區，由于可用水量無法滿足所有用水部門的需求，發生各部門之間的用水沖突，因此迫切需要權衡各部門之間的用水，以消除水資源競爭問題，促進水資源供需之間的平衡［1］。水資源配置是水資源規劃管理的核心工作，合理的水資源分配能夠減少貧困和促進經濟發展，對區域的經濟、 社會和生態產生重要影響［2］。在水資源管理中，氣候的變化、 水資源供應的隨機性、 社會經濟參數以及用水部門的需水量都會影響水資源的可分配量［3］。區域水資源的分配應遵循高效、公平和可持續性的原則［4］，當總水量不能滿足用水部門的需求時，使水資源經濟效益和多個用水部門的用水滿意度最大化是分配的主要目標。此外，為了深入推進環境污染防治，提高水資源利用效率，決策部門需要根據分區污水量產生系數來調整配水，以達到減少區域總污水產生量的目的，因此水資源分配屬于多目標優化問題。

在多目標優化問題中，只追求單一目標的最優化可能會忽視其他目標的發展，分配方案必須協調和綜合權衡多個目標，進而達到整體效益最大化［5］。為了滿足各部門對水資源的需求，促進水資源的高效利用，通常采用數學規劃的方法來優化水資源配置，在不同可分配水量水平下制定合理的分配決策。建立多目標優化配置模型進行水量分配是實現水資源合理分配的有效方法，模型包含了管理層面涉及的多個目標，有助于生成需要考慮多方面權衡的決策。目前，數學和啟發式多目標模型主要有模糊多目標非線性編程模型［6］、 區間多目標編程模型［7］和非支配排序遺傳算法［8］，可以解決多個沖突的管理目標下的合理分配。在水資源分配管理的決策優化問題中，目標函數與變量之間、 約束條件與變量之間往往存在一定的線性函數關系，即使存在某些復雜的非線性函數關系也可采用一些線性逼近方法進行處理［9］，并且線性規劃能夠簡化算法，是解決多變量最優決策的方法，對任何線性規劃問題都能求解。線性規劃的核心思想是強調系統性，即尋找一個盡可能滿足所有目標的滿意解［10］，因此，線性規劃是解決現實世界水資源分配問題的最常用的優化技術之一。

已有文獻中對水資源分配的公平、 效率和可持續發展的多個管理目標進行了研究，但其核心關注點主要是分配水資源所產生的總經濟價值，很少有研究討論公平和效率之間的權衡［11］，并且大多數研究忽略了區域排污的問題，從而缺乏對減少區域污水排放量的探討。本文中針對水資源分配中的公平、 經濟和可持續問題，建立多目標水資源優化配置模型。該模型引入線性規劃算法進行求解，在提高經濟效益的同時減小區域總污水排放量，并設定各用水分區的最低滿意度以確保水資源分配的公平性，為水資源綜合管理提供經濟、 有效的決策支持。通過對青海省龍羊峽水庫的案例研究來驗證模型的有效性和實用性，并結合當地的水量變化情況，建立較高、 較低2種可用水量水平，探究在不同可用水量和不同分區最低用水滿意度下水資源分配方案的變化。

濟南大學學報（自然科學版）第38卷

第3期劉稀琛，等：基于公平-經濟-減排的多目標水資源配置模型

1? 模型構建

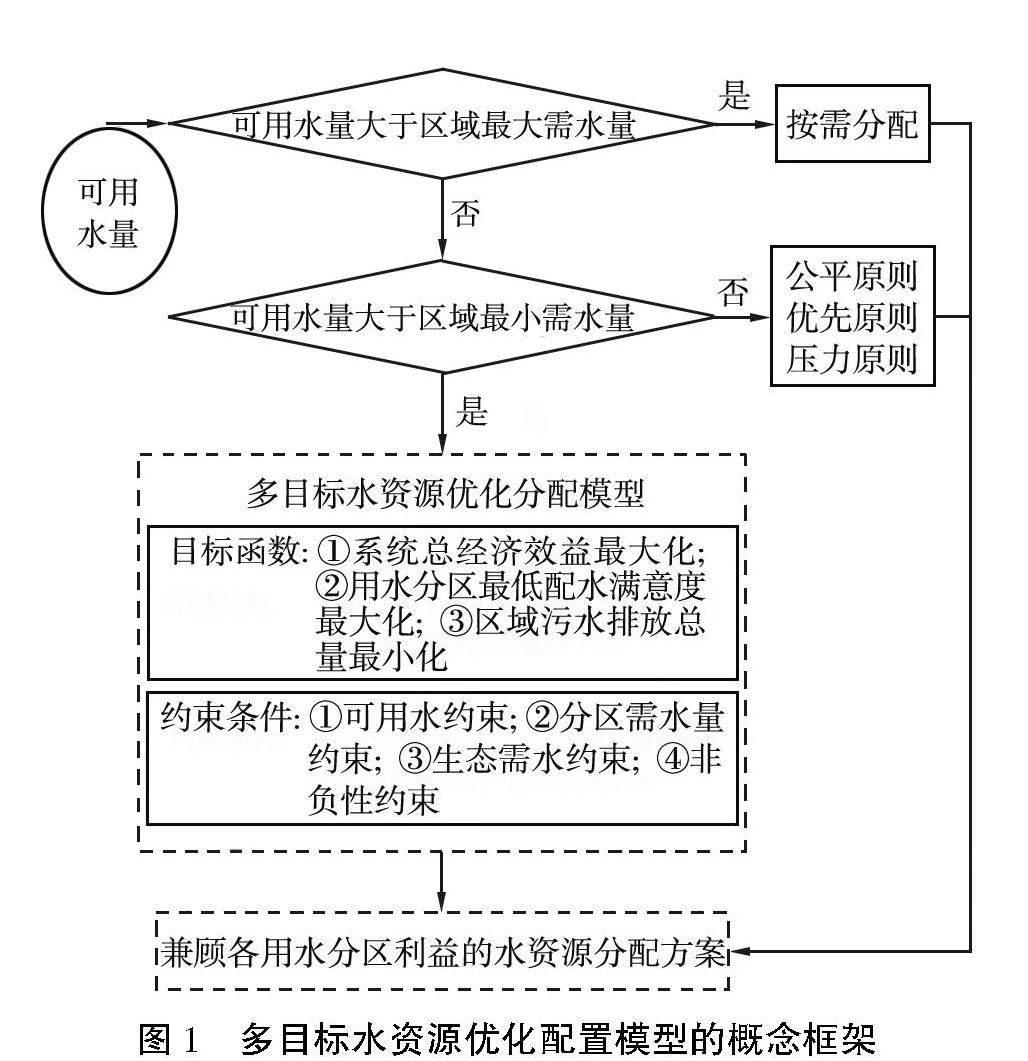
研究區域的總水量用于維持區域的正常工作運轉、 各分區用水、 生態用水、 調控下游水量等。總水量去除區域工作運轉需水、 生態系統需水、 下游出水等水量后，得到的剩余水量為區域可用水量，將其分配給各個用水分區，以獲得較高的系統總經濟效益和各用水分區的配水滿意度，并盡可能地減小研究區域的總污水排放量。構建的多目標水資源優化配置模型用于可用水量介于區域總最小需水量和總最大需水量之間的水資源優化分配。多目標水資源優化配置模型的概念框架如圖1所示。

1.1? 目標函數

多目標水資源優化模型的管理目標包括系統總經濟效益最大化、 各用水分區的最低配水滿意度最大化和污水排放總量最小化3個方面。

目標函數1：實現系統總經濟效益最大化。

系統總經濟效益是指所有用水分區利用所分配的水資源所產生的總經濟收入，計算公式為

max ETB=∑ni=1qi（1-αi）EABi? ，（1）

式中： ETB為研究區域內分配給每個用水分區的水資源所產生的總系統經濟效益； i為研究區域的各個獨立用水分區， i=1， 2， …， n， n為用水分區總數； qi為分配給用水分區i的水量； αi為用水分區i的耗水系數； EABi代表在用水分區i中單位水量可以產生的經濟效益。

目標函數2：實現用水分區的最低配水滿意度最大化。

為了保證各分區區域經濟的平衡發展，在水資源分配中需要考慮公平性［12］。在多目標水資源優化配置模型中，引入滿意度作為衡量水資源分配公平性的評價標準。各分區滿意度的最小值代表了分配方案滿足各部門用水需求的最差水平，因此盡可能的提高分區的最低配水滿意度可以提升分配方案的公平性。

max min Si=qi（1-αi）-qminqmax-qmin ，（2）

式中： Si為在所制定的水資源分配方案下用水分區i的配水滿意度； qmin、 qmax分別為用水分區i的最小需水量和最大需水量。

目標函數3：實現區域污水排放總量最小化。

STE=∑ni=1qi（1-αi）SAEi ，（3）

式中： STE為研究區域在所制定的水資源分配方案下產生的污水排放總量； SAEi為在用水分區i中使用單位水量產生的污水量。

1.2? 約束條件

1）可用水約束。分配給所有用水分區的水量之和不能超過研究地區的總可用水量，即

∑ni=1qi≤W ，（4）

式中W 為研究區域的可用水量。

2）分區需水量約束。分配給各用水分區的水量應介于各分區的最小、最大需水量之間，其中最小需水量為滿足該分區正常運行的最小水量。由于過量的水資源分配會導致資源浪費，因此分配給分區的水量應該受到其最大需水量的限制，即

Di，min≤（1-αi ）qi≤Di，max ，（5）

式中Di，min、 Di，max分別為用水分區i的最小需水量和最大需水量。

3）生態需水約束。由于生態用水對魚類、 野生動物和其他相關環境資源至關重要，因此水資源管理必須優先滿足研究區生態部門的最低用水需求，以實現環境保護和生態可持續性，即

De，min≤We ，（6）

式中： De，min為研究區域生態部門最小用水量； We為分配給生態部門的水量。

4）非負性約束。模型中的所有變量均大于等于0。

1.3? 本文算法

在本文中提出的多目標水資源優化配置模型中，多目標優化模型涉及3個相互沖突管理目標，其中存在著權衡。為了解決多目標優化模型，采用多目標線性規劃方法來尋求最優方案。規劃對象被作為1個系統，并認為系統中所有輸入和輸出關系均為線性關系，根據規劃對象的自然和社會經濟特點，建立數學模型。多目標線性規劃同時考慮多個目標函數，得到同時兼顧各目標利益的合理解［13］。該方法能夠充分體現水資源分配系統功能目標的多重性，從數學角度解決了同時滿足水資源分配規劃中多個目標的要求。同時，本文中確定了不同的用水分區最低配水滿意度，探究不同滿意度標準下的配水方案。

提出的多目標水資源優化配置模型求解過程如下：

步驟1? 根據收集的研究區域歷史相關數據，得出各用水分區的需水量范圍，并建立不同的可用水量情景。

步驟2? 建立多目標線性規劃水資源管理模型，該模型涉及3個相互沖突的管理目標，即系統總經濟效益最大化、 多個用水分區最低配水滿意度最大化和區域總污水排放量最小化。

步驟3? 在給定的約束條件下獲得不同條件要求下的最優分配方案。

步驟4? 重復步驟3，獲得不同可用水量和不同用水分區最低配水滿意度下的最優分配方案。

2? 研究案例

2.1? 研究區域概況

龍羊峽水庫位于青海省共和縣、 貴南縣的交界處， 是黃河上游干流的唯一一座多年調節水庫， 控制了黃河天然徑流的40%以上，總庫容為2.47×1010 m3， 調節庫容為1.936×1010 m3， 對黃河徑流具有很強的調節能力［14］。龍羊峽水庫為周邊地區的農業、 生活、 工業和生態等部門提供用水，兼有防洪、 灌溉、 防凌、 養殖等綜合效益，同時兼顧調控下游水量。本文中根據龍羊峽水庫的地理位置，以及青海省的水源分布情況，以龍羊峽水庫可用水為規劃對象，選擇西寧市、海東市、海南藏族自治州（簡稱海南州）和黃南藏族自治州（簡稱黃南州）4個分區作為水資源分配管理中用水研究對象。

2.2? 數據來源

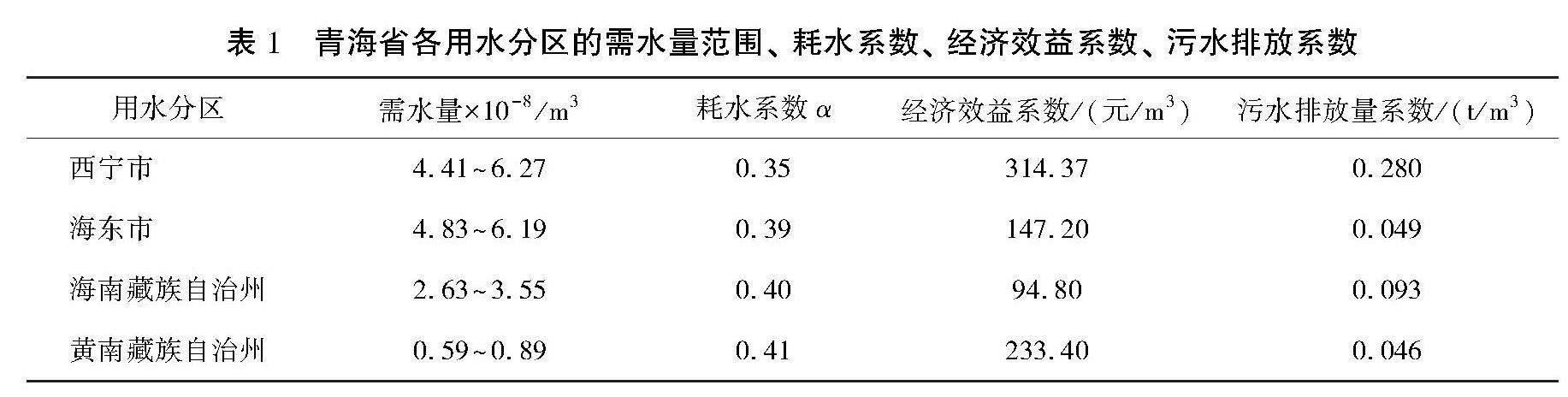
本文中采用的相關數據為過去9 a（2013—2021年）的平均值。 龍羊峽水庫蓄水量、 入庫水量和出庫水量數據采用水利部黃河水利委員會官方徑流數據的還原成果［15］， 區域其他流入量（如降雨量、 地表溪流、 地下水等）、 研究區域用水分區的耗水系數和蒸發量均根據《青海省水資源公報》中的數據［16-24］計算得出， 區域可用水量結合以上相關水量數據計算得出。 根據可用水量計算結果， 本文中設定2種不同的可用水量水平分別為2.293×109、 2.592×109 m3。 在生態需水方面，采用Tennant提出的方法［25］，計算得出區域生態系統的最小需水量約為1.17×108 m3。 各用水部門的最大、 最小需水量通過評估來自《青海省水資源公報》的歷史用水數據， 在實際情況的基礎上推算得出。 研究區域每個用水分區的單位水經濟效益根據《青海統計年鑒》［26］中的經濟數據和《青海省水資源公報》中的用水數據計算得出。 用水分區的污水排放量數據來自《中國城市建設統計年鑒》［27］。相關參數見表1。 隨著生產力的發展， 未來相關經濟、 用水數據發生變化可對模型代入數據進行調整。

2.3? 問題描述

本文中將建立的多目標水資源優化配置模型應用于龍羊峽水庫，規定用水分區對于的最低配水滿意度，為研究區域在不同可用水量水平下的綜合水資源管理提供具有成本效益和環保效應的決策支持。研究區域通過結合水庫水量數據和區域相關數據獲得總可用水量。為了保證區域的生態可持續性，水量首先用于滿足研究區域生態系統的需水量，剩余水量作為該模型的可用水量分配給各個用水分區。水資源的規劃分配考慮到系統總經濟效益最大化、 4個用水分區的最低配水滿意度最大化以及區域總污水排放量最小化。

3? 結果分析

在同一可用水量下設定不同用水分區的最低配水滿意度。在較低可用水量、 較高可用水量下，通過建立的多目標水資源優化配置模型得到的符合不同最低配水滿意度要求的最優水資源分配方案分別如表2、 3所示。

在較低可用水量水平時，用水分區的最低配水滿意度的最大值為0.4。隨著最低配水滿意度的提升，各用水分區的平均滿意度呈現明顯的上升趨勢，區域總經濟效益和總污水排放量均呈現明顯的下降趨勢。由此可以說明最低配水滿意度最大化目標、 經濟最大化目標和污水排放最小化目標存在沖突。在不同的最低配水滿意度下，多目標水資源優化配置模型總是趨向于優先配水給西寧市，原因是該分區雖然污水排放系數較大，但較小的耗水系數和較大的單位水經濟效益系數使其在多目標配水中處于優先地位。最低配水滿意度的提升使得區域的配水更加公平，各用水分區的滿意度逐漸趨近。因為當最低配水滿意度提升時，多目標水資源優化配置模型需要將滿意度較高的分區配水調入滿意度較低的分區，從而滿足設置的最低配水滿意度要求，即西寧市的配水逐漸減少，其他3個分區的配水量逐漸增多。

在較高可用水量水平時，用水分區的最低配水滿意度的最大值為0.8。區域總經濟效益總體呈現下降趨勢，平均滿意度和總污水排放量增長趨勢不明顯，但在最低配水滿意度上升至0.7時，平均滿意度下降，最低配水滿意度上升至0.8時，總污水排放量減小。該用水量水平時，多目標水資源優化配置模型仍更傾向于優先滿足西寧市的配水。當設定的最低配水滿意度增大時，西寧市的配水量幾乎不變，海東市和黃南州的配水開始減少，海南州的配水量逐漸增加，以滿足最低配水滿意度要求。由于西寧市和黃南州的單位水量經濟效益最高，因此這2個分區的配水減少，導致整個研究區域的經濟效益降低。

與僅以總經濟效益最大化或總污水排放量最小化的單目標配置模型相比，多目標水資源優化配置模型所得方案的滿意度、 經濟效益和污水排放各項指數均介于2個單目標模型之間。與僅以區域總污水排放量最小化為目標得到配水方案相比，多目標水資源優化配置模型在較低可用水量、 較高可用水量下得到的配水方案的區域總經濟效益最高可分別增加2.57×1010、 1.85×1010元。與僅以系統總經濟效益最大化為目標得到配水方案相比，多目標水資源優化配置模型在較低可用水量下的配水方案的總污水排放量減少1.8×107 t；在較高可用水量下，當設定的用水分區最低配水滿意度大于0.3時，多目標水資源優化配置模型配水方案產生的總污水排放量開始大于以系統總經濟效益最大化為目標的單目標配水方案的。

上述結果分析表明，多目標水資源優化配置模型能夠實現污水減排和經濟效益之間的權衡，得到最佳的配水方案；但是，如果僅提升最低配水滿意度，就將導致污水排放量增加和經濟效益降低。各地政府需根據地區實際需求，確定適當的最低配水滿意度水平，進而采用該滿意度要求下多目標水資源優化配置模型計算得到的最佳配水方案。此外，較高可用水量下的用水分區平均滿意度、 總經濟效益和總污水排放量均明顯高于較低可用水量下的，說明可用水量的增加能夠為分區提供更充足的資源，有效促進區域經濟發展，因此，相關部門需要根據歷史數據合理制定蓄水策略，制定合理的計劃來開發水文設施，從而在合理范圍內提升可用水量，同時應加強基礎設施建設，提升污水處理能力，維持生態環境安全。

4? 結論

本文中以系統總經濟效益最大化、 用水分區最低配水滿意度最大化和區域總污水排放量最小化為目標，建立了多目標線性規劃水資源優化配置模型，以支持不同可用水情景下的水資源管理。以青海省龍羊峽水庫的水資源優化分配為例證明了該模型具有良好的實用性和可行性。在較低、 較高可用水量水平設置了不同的用水分區最低配水滿意度，得到不同的最優配水方案。主要結論如下：

1）盲目提升最低配水滿意度會降低地方的經濟效益。決策部門可以根據偏好設定適當的最低配水滿意度，從而選擇多目標水資源優化配置模型生成的最優配水方案。

2）多目標水資源優化配置模型生成的配水方案可使區域總經濟效益可提升約2.57×1010元，總污水排放量可減少約1.8×107 t，有助于研究區域的經濟發展和污水減排，提升區域水資源利用效率。

3） 可用水量的增加會顯著影響區域經濟效益和用水分區配水滿意度，因此相關部門應采取措施提升區域蓄水能力，以在合理范圍內增加可用水量。加強基礎設施建設，提升區域污水處理能力和質量，保證水環境安全。

參考文獻：

［1］? DIVAKAR L， BABEL M S， PERRET S R， et al. Optimal allocation of bulk water supplies to competing use sectors based on economic criterion： an application to the Chao Phraya River Basin， Thailand［J］. Journal of Hydrology， 2011， 401（1）： 22.

［2］? WANG J Q， QIN L J， HE H S. Assessing temporal and spatial inequality of water footprint based on socioeconomic and environmental factors in Jilin Province， China［J］. Water， 2019， 11（3）： 521.

［3］? NEMATIAN J. An extended two-stage stochastic programming approach for water resources management under uncertainty［J］. Journal of Environmental Informatics， 2016， 27（2）： 72.

［4］? MALGHAN D. On the relationship between scale， allocation， and distribution［J］. Ecological Economics， 2010， 69（11）： 2261.

［5］? ZHOU Y L， GUO S L， XU C Y， et al. Integrated optimal allocation model for complex adaptive system of water resources management （I）： methodologies［J］. Journal of Hydrology， 2015， 531： 964.

［6］? LI M， FU Q， SINGH V P， et al. An intuitionistic fuzzy multi-objective non-linear programming model for sustainable irrigation water allocation under the combination of dry and wet conditions［J］. Journal of Hydrology， 2017， 555： 80.

［7］? LI M， FU Q， SINGH V P， et al. An interval multi-objective programming model for irrigation water allocation under uncertainty［J］. Agricultural Water Management， 2018， 196： 24.

［8］? NAGHDI S， BOZORG-HADDAD O， KHORSANDI M， et al. Multi-objective optimization for allocation of surface water and groundwater resources［J］. Science of the Total Environment， 2021， 776： 146026.

［9］? 楊文昌. 多目標線性規劃在項目管理中的應用［J］. 中國管理信息化， 2013， 16（4）： 61.

［10］? 牛映武， 楊文鵬， 郭鵬， 等. 運籌學［M］. 2版. 西安： 西安交通大學出版社，2006.

［11］? YUAN M K， CHEN X D， LIU G Z， et al. Coordinated allocation of water resources and wastewater emission permits based on multi-objective optimization model： from the perspective of conflict between equity and economic benefits［J］. Journal of Cleaner Production， 2022， 372： 133733.

［12］? SHUAI Y H， HE X P， YAO L M. Robust optimization with equity and efficiency framework for basin-wide water resources planning［J］. Journal of Environmental Management， 2022， 321： 115834.

［13］? 翁文斌， 蔡喜明， 史慧斌， 等. 宏觀經濟水資源規劃多目標決策分析方法研究及應用［J］. 水利學報， 1995（2）： 1.

［14］? 羅紅春， 冀鴻蘭， 牟獻友， 等. 黃河石嘴山站水沙變化及趨勢分析［J］. 南水北調與水利科技， 2019， 17（4）： 193.

［15］? 水利部黃河水利委員會.水情信息［EB/OL］. （2013-01-01）［2021-12-31］. http：//www.yrcc.gov.cn/.

［16］? 青海省水利廳水文水資源管理處. 2013年青海省水資源公報［R］. 西寧： 青海省水利廳， 2014.

［17］? 青海省水利廳水文水資源管理處. 2014年青海省水資源公報［R］. 西寧： 青海省水利廳， 2015.

［18］? 青海省水利廳水文水資源管理處. 2015年青海省水資源公報［R］. 西寧： 青海省水利廳， 2016.

［19］? 青海省水利廳水文水資源管理處. 2016年青海省水資源公報［R］. 西寧： 青海省水利廳， 2017.

［20］? 青海省水利廳水文水資源管理處. 2017年青海省水資源公報［R］. 西寧： 青海省水利廳， 2018.

［21］? 青海省水利廳水文水資源管理處. 2018年青海省水資源公報［R］. 西寧：青海省水利廳， 2019.

［22］? 青海省水利廳水文水資源管理處. 2019年青海省水資源公報［R］. 西寧： 青海省水利廳， 2020.

［23］? 青海省水利廳水文水資源管理處. 2020年青海省水資源公報［R］. 西寧： 青海省水利廳， 2021.

［24］? 青海省水利廳水文水資源管理處. 2021年青海省水資源公報［R］. 西寧： 青海省水利廳， 2022.

［25］? TENNANT D L. Instream flow regimens for fish， wildlife， recreation and related environmental resources［J］. Fisheries， 1976， 1（4）： 6.

［26］? 青海省統計局.青海統計年鑒［EB/OL］. （2013-01-01） ［2021-12-31］. http：//tjj.qinghai.gov.cn/tjdata/qhtjnj/.

［27］? 中華人民共和國住房和城鄉建設部. 中國城市建設統計年鑒［EB/OL］. （2013-01-01）［2021-12-31］. https：//www.mohurd. gov.cn/gongkai/fdzdgknr/sjfb/tjxx/jstjnj/index.html

（責任編輯：于海琴）