基于修正割線方程的BB梯度法

摘 要：將修正的割線方程和BB梯度法結合起來，從而得到一類修正的BB步長，再利用Zhang-Hager非單調線搜索，提出一個改進的BB梯度方法（MB法）。在一定的假設下，MB法是具有全局收斂性的。同時對MB法和同類型的幾個BB方法進行大量的數值試驗，結果表明MB法的數值效果是最好的。

關鍵詞：Barzilai-Borwein梯度法；非單調線搜索；無約束優化；改進割線方程

中圖分類號：O224? ?文獻標識碼：A文章編號：1674-0033（2024）02-0022-04

引用格式：楊爽藝.基于修正割線方程的BB梯度法[J].商洛學院學報，2024，38（2）：22-25.

BB Gradient Method Based on Modified Secant Equation

YANG Shuang-yi

（College of Mathematical Sciences， Chongqing Normal University， Shapingba? 401331， Chongqing）

Abstract： A modified BB gradient method （MB method） is proposed by combining the modified secant equation with the BB gradient method， thus obtaining a class of modified BB steps， and then using Zhang-Hager nonmonotonic line search. Under certain assumptions， the MB method is globally convergent. A large number of numerical experiments are also conducted on the MB method and several BB methods of the same type， and the results show that the MB method is the best numerically.

Key words： Barzilai-Borwein gradient method; nonmonotone line search; unconstrained optimization; modified secant equation

對于求解無約束優化問題：

f（x）? ? （1）

其中，f（x）：Rn→R為連續可微函數，n是變量的個數，x為決策變量。梯度法是解決這類問題最簡單的方法之一，其迭代格式為：

xk+1=xk-αkgk? ? （2）

其中，gk是f在xk處的梯度，αk是步長，不同的步長對應著不同的梯度法。

文獻[1]在最小二乘意義下去近似標準割線方程Bksk-1=yk-1和Hkyk-1=sk-1中的Bk和Hk，得到步長的兩個表達式：

[αBB1][k]=

（3）

[αBB2][k]=

其中，sk-1=xk-xk-1，yk-1=gk-gk-1。

[αBB1][k]和[αBB2][k]被稱為兩點步長或者BB步長，對應的梯度法被稱為BB梯度法，簡稱BB法。BB法擁有更快的收斂速度，同時還避免了一些復雜的計算。BB法的良好性能激起了研究者對BB法的研究。文獻[2]估計迭代點的單純形梯度，對BB法進行改進。文獻[3]利用循環策略去更新BB步長。盡管許多研究者提出了一些改進的BB法，但對最優的BB梯度法還未達成共識。文獻[4]基于文獻[5]提出的割線方程，推導出了6個修正的BB步長。文獻[6]基于文獻[7]提出的修正割線方程，并提出了改進BB步長。這些方法都表明，從割線方程角度去修正的BB法是可行的，但是數值性能上還存在一定缺陷。基于此，本文在文獻[8]的研究基礎上，進一步優化，結合一個具有更好性質的割線方程來修正BB法。

1? 修正的BB梯度法（MB）的算法

在文獻[9]中，令f（x）的Hessian矩陣Q（xk）取近似Bk和Bk+1，從而提出一個改進的割線方程：

Bksk-1=wk-1=2yk-1+uk-1? ? ? ?（4）

其中，uk-1=gk。

將這個割線方程和BB法結合起來，用wk-1代替原BB1步長中的yk-1，則得到一個新的步長：

[αMB][k]=? ? ? ? （5）

其中，sk-1=xk-xk-1，yk-1=gk-gk-1。

基于文獻[10]中的算法框架，提出了一個修正的BB型算法（MB法）。

選擇初始步長后，利用Zhang-Hager非單調線搜索[11]來計算后面的近似步長。

步驟1? 給定初始值x0∈Rn，λmax≥λmin≥0，ε，γ∈（0，1），ηk∈[0，1]，0<σ1<σ2<1；計算f0，令C0=f0，Q0=1，α0=1，k=0。

步驟2? 若‖gk‖∞≤ε，停止迭代；否則，令dk=-αkgk。

步驟3? 計算步長αk（非單調線搜索）。

先令t=1，若滿足：

f（xk+αkdk）≤Ck+γtαkg[k][T]dk? ? ? ?（6）

再令xk+1=xk+tαkdk，轉向步驟4。否則，選擇t∈[σ1t，σ2t]，轉向步驟2。

步驟4? 用式（5）和式（6）計算步長，若αk<0，則令αk=λmax。否則，令αk=min{λmax，max{λmin，αk}}，轉向步驟5。

步驟5? 選擇ηk∈[ηmin，ηmax]，并計算：

Qk+1=ηkQk+1，Ck+1=。

步驟6? 令k=k+1，轉向步驟2。

2? 收斂性分析

假設1? 水平集Ω={x∈R：f（x）≤f（x0）}有界，即存在一個常數M>0，有：

‖x‖≤M，?x∈Ω ? ? ? ?（7）

假設2? 目標函數f在Ω的某個鄰域N連續可微，且梯度▽f Lipschitz連續，即存在常數L>0，有：

‖g（x）-g（x*）‖≤L‖x-x*‖， ?x，x*∈N? ? ? ? （8）

引理1? 設Ak是關于k的平均函數值，即Ak=fi。如果對于任意k都滿足▽f（xk）dk≤0，那么在第k次迭代過程中，對任意的ηk，都有fk≤Ck≤Ak。

證明：令Dk（t）= ? ? ? ? ? ? （9）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?其中，D：R→R。

求導可得：

D[′][k]（t）= ? ? ? ? ? ? ? ? ? ? ? ?（10）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?由于fk≤Ck-1，所以對任意的t≥0，都有D[′][k]（t）≥0，即Dk（t）是單調遞增的。

故有：

fk=Dk（0）≤Ck ? ? ? ? ? ? ? ? ? ? ?（11）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 即Ck有下界，然后用歸納法證明Ck有上界。

當k=0時，有C0=f（x0）成立。

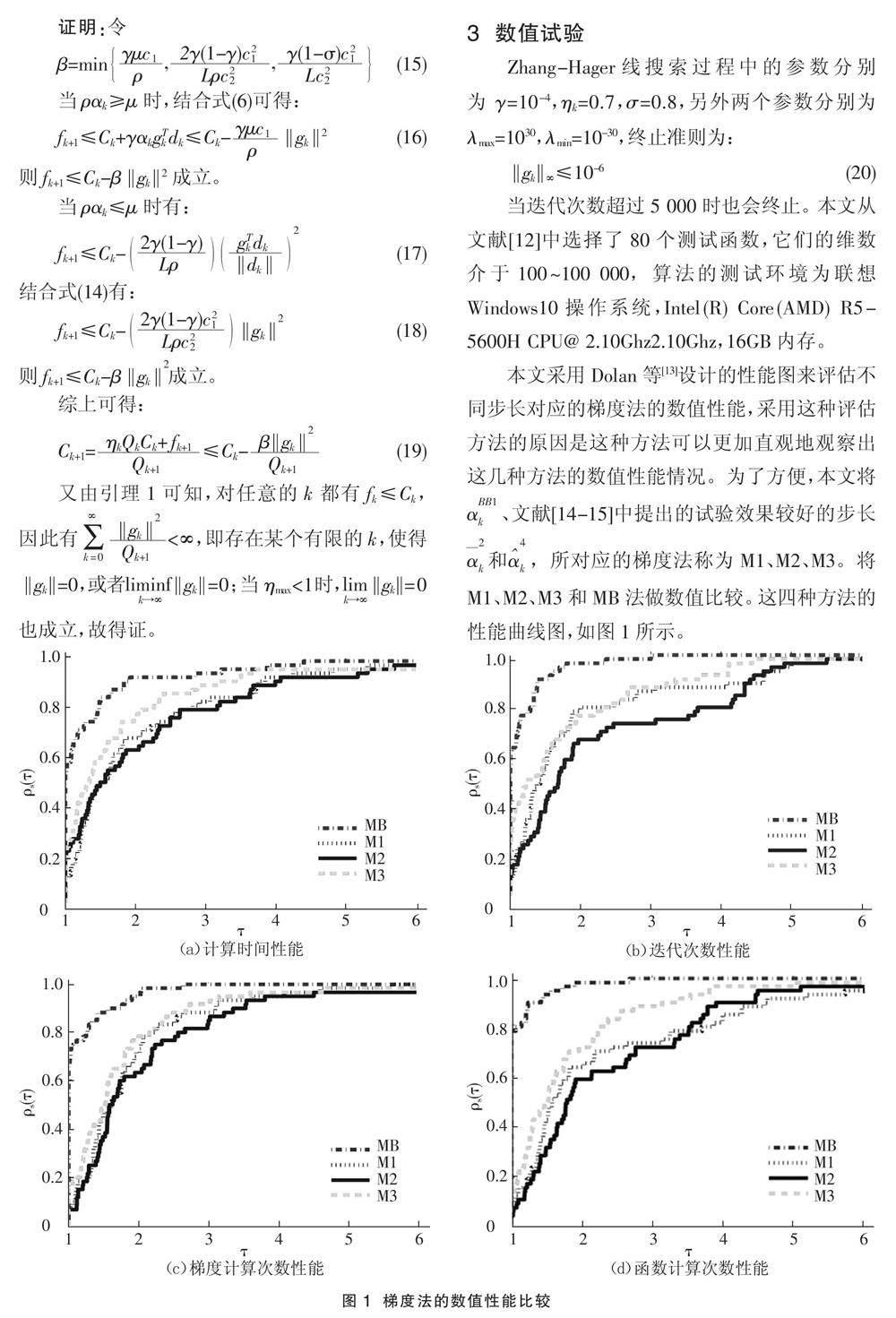
現假設對任意的0≤j

Qj+1=1+ηj-m≤j+2 ? ? ? ? ? ? ? （12）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 又由于Dk（t）是單調遞增的，則有：

Ck=Dk（Qk-1）≤Dk（k）=≤=Ak （13）

結合式（11）和式（13）可得fk≤Ck≤Ak，故得證。

進一步，在[αmin，αmax]中選擇步長αk，則存在兩個常數c1和c2，使得搜索方向dk滿足：

g[k][T]dk≤-c1‖gk‖2，‖dk‖≤c2‖gk‖，?k∈R （14）

定理1? 在假設1和假設2條件下，設MB法產生的迭代點列為{xk}，那么就存在某個有限的k，使得‖gk‖=0，或者‖gk ‖=0。進一步，當ηmax<1時，有‖gk‖=0。因此，迭代的每個收斂子序列都會接近一個點x*，其中▽f（x*）=0。

證明：令

β=min

，

，

（15）

當ραk≥μ時，結合式（6）可得：

fk+1≤Ck+γαkg[k][T]dk≤Ck-‖gk ‖2（16）

則fk+1≤Ck-β‖gk ‖2成立。

當ραk≤μ時有：

fk+1≤Ck-

（17）

結合式（14）有：

fk+1≤Ck-

‖gk ‖（18）

則fk+1≤Ck-β‖gk ‖成立。

綜上可得：

Ck+1=≤Ck-? ?（19）

又由引理1可知，對任意的k都有fk≤Ck，因此有<∞，即存在某個有限的k，使得‖gk‖=0，或者‖gk‖=0；當ηmax<1時，‖gk‖=0

也成立，故得證。

3? 數值試驗

Zhang-Hager線搜索過程中的參數分別為γ=10-4，ηk=0.7，σ=0.8，另外兩個參數分別為λmax=1030，λmin=10-30，終止準則為：

‖gk ‖∞≤10-6（20）

當迭代次數超過5 000時也會終止。本文從文獻[12]中選擇了80個測試函數，它們的維數介于100～100 000，算法的測試環境為聯想Windows10操作系統，Intel（R） Core（AMD） R5-5600H CPU@ 2.10Ghz2.10Ghz，16GB內存。

本文采用Dolan等[13]設計的性能圖來評估不同步長對應的梯度法的數值性能，采用這種評估方法的原因是這種方法可以更加直觀地觀察出這幾種方法的數值性能情況。為了方便，本文將α、文獻[14-15]中提出的試驗效果較好的步長和，所對應的梯度法稱為M1、M2、M3。將M1、M2、M3和MB法做數值比較。這四種方法的性能曲線圖，如圖1所示。

數值試驗通過求解大量問題，將四種梯度法從計算時間、迭代次數、梯度計算次數和函數計算次數四個維度進行比較。圖1（a）是對四種梯度法的計算時間的比較，發現MB法解決問題花費的計算時間最少。圖1（b）是對四種梯度法的迭代次數的比較，發現MB法迭代次數最少。圖1（c）是對四種梯度法的梯度計算次數的比較，發現MB法的梯度計算次數最少。圖1（d）對四種梯度法的函數計算次數的比較，發現MB法的函數計算次數最少。

從圖1可見，在計算時間、迭代次數、梯度計算次數和函數計算次數上看，MB法始終表現得最好，這就說明，MB法具有比較好的數值效果。

4? 結語

將改進割線方程和BB梯度法結合起來，得到一個新的步長——MB步長，再結合非單調線搜索得到MB法。通常的步長只使用了當前迭代點和上一迭代點的值及梯度值，但是MB步長還使用了當前迭代點和上一迭代點的函數值，因此充分利用了迭代點的信息。通過收斂性分析得到MB法是全局收斂的，并且不需要對目標函數作任何的凸性假設。數值試驗結果表明，從時間、迭代次數、函數計算次數和梯度計算次數上來看，MB法都具有較好的計算效率。

參考文獻：

[1]? JONATHAN B， BORWEIN J M. Two point step-size methods[J].Ima Journal on Numerical Analysis，1988（1）：1.

[2]? 鄭鵬遠，李琴，孫忠林.基于Barzilai-Borwein梯度法的多微電網系統遞階優化調度算法[J].科學技術與工程，2020，20（30）：12443-12451.

[3]? 楊奕涵.帶有循環策略的自適應截斷BB梯度法研究[J].黑龍江科學，2023，14（20）：54-57.

[4]? BABAIE-KAFAK S， FATEMI M. A modified two-point stepsize gradient algorithm for unconstrained minimization[J].Optimization Methods and Software，2013，28（5）：1040-1050.

[5]? LI D H， FUKUSHIMA M. A modified BFGS method and its global convergence in nonconvex minimization[J].Journal of Computational and Applied Mathematics，2001，129（1-2）：15-35.

[6]? 鄭燏濤.Barzilai-Borwein梯度法及其在優化算法中的應用[D].蘭州：蘭州大學，2018：11-24.

[7]? FORD J A， MOGHRABI I A. Multi-step quasi-Newton methods for optimization[J].Journal of Computational and Mathematics，1994，50（93）：305-323.

[8]? 陳旦.基于混合割線方程修正的BB梯度法[J].綿陽師范學院學報，2023，42（2）：8-14.

[9]? HASSAN B A， MOGHRABI I A R. A modified secant equation quasi-Newton method for unconstrained optimization[J].Journal of Applied Mathematics and Computing，2023，69：451-464.

[10] BIGLARI F， SOLIMANPUR M. Scaling on the spectral gradient method[J].Journal of Optimization Theory and Applications，2013，158（2）：626-635.

[11] HAGER W W， ZHANG H. A new conjugate gradient method with guaranteed descent and an efficient line search[J].SIAM Journal on Optimization，2005，16（1）：170-192.

[12] GOULD N I M， ORBAN D， TOINT P L. CUTEr and SifDec： a constained and unconstrained testing environment， revisited[J].Acm Trainscations on

Mathematical Software，2003，29（4）：373-394.

[13] DOLAN E， MOR? J J. Benchmarking optimization software with performance profiles[J].Mathematical Programming，2001，91：201-213.

[14] XIAO Y， WANG Q， WANG D. Notes on the Dai-Yuan-Yuan modified spectral gradient method[J].Journal of Computational and Applied Mathematics，2010，234（10）：2986-2992.

[15] ZHANG J Z， DENG N Y， CHEN L H. New quasi-newton equation and related methods for unconstrained optimization[J].Journal of Optimization Theory and Applications，1999，102（1）：147-167.