基于高斯小波函數(shù)和線性表達法的開口板自由振動特性研究

郭文杰, 柴天建, 顏建偉, 洪 顯

(華東交通大學 軌道交通基礎設施性能檢測與保障國家重點實驗室,南昌 330013)

開口板是一種典型的工程結(jié)構(gòu)形式,廣泛應用于船舶、鐵道、建筑、機械等領域,例如隱身艦船集成化上層建筑的設備口開孔[1]、軌道板開口內(nèi)置鋼彈簧浮置減振板[2]。開口板會引起動力學性能的變化,存在與開口附近設備產(chǎn)生共振的風險,還與向周圍輻射的噪聲有直接關系。開口尺寸、形狀和邊界條件是開口板振動特性影響的重要因素[3],因此研究開口板結(jié)構(gòu)動力特性,對工程結(jié)構(gòu)設計具有重要的實際意義。

針對開口板振動問題,主要有半解析法和數(shù)值方法[4-5]。數(shù)值方法主要為有限單元法,邱昌林等[6]采用有限元法研究了鋼板開圓形口時的自振頻率,張媛等利用有限元分析了不同開口尺寸對薄板自振頻率的影響。傳統(tǒng)能量法(如瑞利里茲法[7-9])在結(jié)構(gòu)動力學中被廣泛使用,它提供了一種快速而精確的方法來推導和求解給定系統(tǒng)的運動方程。例如Mundkur等[10]基于瑞利里茲法使用正交多項式函數(shù)分析了開口板的振動。Avalos等[11]應用Rayleigh-Ritz法對開兩矩形口的矩形板進行計算,分析了不同大小、開口位置等對固有頻率的影響。Larrondo等[12]應用Rayleigh-Ritz法對變厚度矩形多開口平板的自由振動進行分析,并對不同開口位置,開口大小對頻率的影響進行分析。瑞利里茲方法依賴于位移形函數(shù)[13-14],形函數(shù)必須滿足問題的各種約束條件。一些研究人員采用人工彈簧法[15-17]處理邊界條件,將約束問題轉(zhuǎn)變?yōu)闊o約束問題,例如:王旻昊等[18]采用人工彈簧法模擬邊界條件,計算得到開口板的固有頻率和響應振型,并討論了開口尺寸和邊界條件對自振特性的影響;張俊等采用人工彈簧模型模擬不同的邊界條件。位移容許函數(shù)會影響求解精度和準確性,改進傅里葉級數(shù)法[19]可以克服傳統(tǒng)傅里葉級數(shù)在邊界處不連續(xù)線性,可以適應結(jié)構(gòu)的一般邊界條件。例如:邱永康等[20]利用改進傅里葉級數(shù)方法作為開口板位移場的形函數(shù),分別研究了復雜邊界條件下單開口和多開口矩形板的自振特性;Shi等[21]應用改進的傅里葉級數(shù)方法對一般邊界條件下多個矩形開口的矩形板的自由振動特性進行了分析,計算了內(nèi)部開口和外部開口的固有頻率,并得出了振型圖。

人工彈簧-瑞利里茲法,將有邊界約束問題轉(zhuǎn)化為無約束問題,對于邊界約束的處理具有相當?shù)膬?yōu)點。人工彈簧-瑞利里茲法是一類有參數(shù)方法,模型的收斂性在很大程度上取決于彈簧剛度的值。彈簧剛度越大,高階模式的收斂性越好,但當彈簧剛度取值過大時可能導致矩陣奇異問題[22]。此外,形函數(shù)的選擇也是影響瑞利里茲法求解精度的關鍵因素。現(xiàn)有研究中常采用的位移形函數(shù)有切比雪夫多項式級數(shù)[23]等和改進傅里葉級數(shù)作為全局性函數(shù),在計算非開口板或厚度連續(xù)變化板時具有較好的收斂性,但在計算非連續(xù)變化板厚的開口板時,則需要更多的級數(shù)項才能滿足計算精度。

本文以能量法為基本框架,采用線性表達法(linear expression method,LEM)來處理各種邊界條件,將有邊界約束問題轉(zhuǎn)變?yōu)闊o約束問題。基本思路是通過高斯消元法找到約束條件矩陣中線性無關的列向量,將位移形函數(shù)的未知系數(shù)轉(zhuǎn)變?yōu)榫€性無關系數(shù)列向量的線性表達,從而將有約束問題轉(zhuǎn)變?yōu)闊o約束問題;根據(jù)能量法基本原理,構(gòu)建了拉格朗日能量泛函,并對位移形函數(shù)的系數(shù)進行變分求極值,將振動問題轉(zhuǎn)化成求解特征值和特征向量的問題。與人工彈簧法相比,不需要設置彈簧剛度等參數(shù),避免了矩陣可能奇異的問題。選取高斯小波函數(shù)[24-25]作為開口板的位移形函數(shù),以確保能夠準確捕捉開口位置處的局部化特征。以四邊簡支和四邊固定的開口板為例進行分析,結(jié)合有限元方法計算結(jié)果,討論解的收斂性和準確性。研究了不同開口尺寸、形狀對自振頻率的影響。計算了不同邊界約束條件下多開口板的自振頻率。線性表達法使用簡便,編程快捷,可廣泛應用于有約束問題分析中。

1 理論分析

1.1 開口矩形板的力學模型

本文以矩形薄板中心開圓孔為具體研究對象,以中點為坐標原點建立直角坐標系,如圖1所示。板長2a,寬2b,厚度h。定義邊界條件表示符號如下:固定邊界C,簡支邊界S,自由邊界F,從左側(cè)開始,逆時針順序表示四邊邊界約束。例如:SFSF表示左右邊簡支,上下邊自由;SSSS表示四邊自由。

圖1 矩形開口板示意圖Fig.1 Schematic diagram of rectangular open plate

1.2 位移形函數(shù)

假設離面位移w表示為基函數(shù)ξi(x,y)和一組權(quán)重系數(shù)dk(t)的組合,即

w(x,y,t)=dTξ(x,y)

(1)

其中,

ξ(x,y)=φ(x)?ψ(y),
φ=[φ1(x),φ2(x),…,φi(x),…,φm(x)]T,
ψ=[ψ1(y),ψ2(y),…,ψi(y),…,ψn(y)]T

式中: ?為克羅內(nèi)克積;φ為x方向的容許梁函數(shù);ψ為y方向的容許梁函數(shù)。

針對開口板厚度局部突變,本文采用具有局域化特性的高斯小波函數(shù)描述位移形函數(shù)[26-27],以捕捉厚度變化區(qū)域的波動特征。據(jù)此,基函數(shù)φi(x)、ψi(y)表示為

(2)

式中:p、q為x和y方向的伸縮因子;k、r為平移因子。

本節(jié)以x方向形函數(shù)φi(x)為例,對高斯小波函數(shù)式(2)分析。如圖2所示,當平移因子k=0時,高斯小波函數(shù)的支撐范圍為[-4×2-p, 4×2p],伸縮因子p取值越大,支撐范圍越小,函數(shù)的分辨率越高[28-29]。為使函數(shù)支撐范圍分辨率滿足結(jié)構(gòu)的尺寸要求,伸縮因子需滿足式(3)的限制條件。

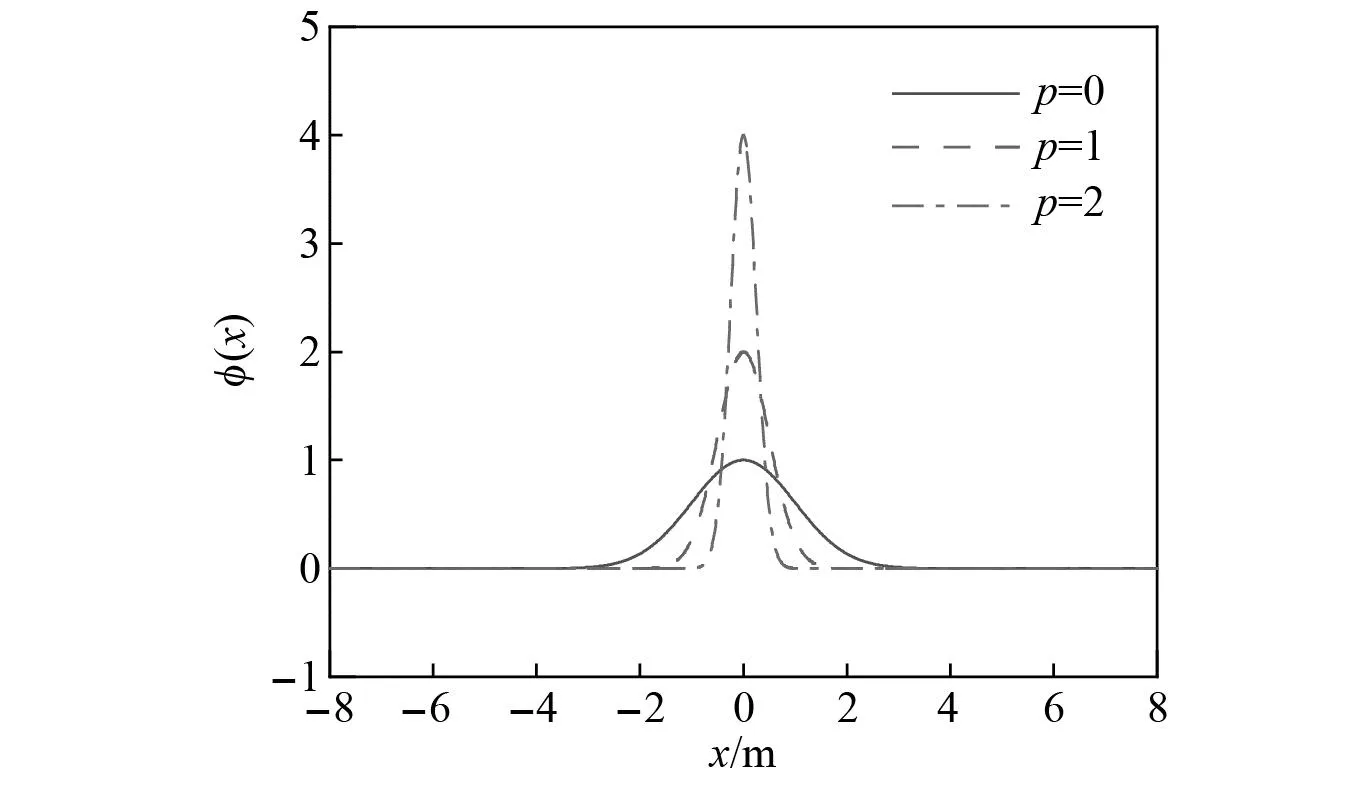
圖2 不同伸縮因子對應的高斯曲線Fig.2 Gaussian curves corresponding to different scaling factors

(3)

式中, ceil(·)為向上取整數(shù)。

圖3所示,當p=0時,高斯小波函數(shù)的支撐范圍為[-4+k,4+k],隨著平移因子增大,支撐范圍從左側(cè)移到右側(cè)。為使函數(shù)支撐范圍覆蓋結(jié)構(gòu)的尺寸,平移因子需滿足式(4)的限制條件。

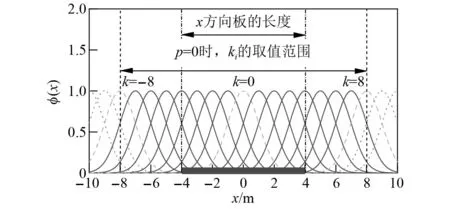
圖3 不同平移因子對應的高斯曲線Fig.3 Gaussian curves corresponding to different translation factors

(4)

式中, floor(·)為向下取整數(shù)。

1.3 運動方程的建立

根據(jù)Kirchhoff-Love薄板理論,開口板的彎曲應變能為

(5)

令

式中:D=(Eh3)/[12(1-μ2)],E和μ分別為薄板材料彈性模量和泊松比;K為整體結(jié)構(gòu)應變能的剛度矩陣。

厚度函數(shù)h(x,y)為

(6)

式中:p(x0,y0)為圖1所示開口板坐標系內(nèi)任意一點的橫坐標和縱坐標;S為圓孔開口區(qū)域。

開口板的動能為

(7)

式中:ρ為薄板材料的密度;M為整體結(jié)構(gòu)的質(zhì)量矩陣。

整體結(jié)構(gòu)的能量泛函可表示為

(8)

1.4 利用線性表達法考慮邊界條件

四邊簡支開口板的邊界條件如下

w(x,y,t)|x=±a=0,w(x,y,t)|y=±b=0

(9)

式(9)意味著形函數(shù)(1)中的權(quán)重系數(shù)d并非是獨立的,而是存在線性相關性。

傳統(tǒng)的能量法,通常采用構(gòu)造滿足位移邊界條件的位移函數(shù)w(x,y)[30],將自由振動的二階微分方程問題轉(zhuǎn)化為特征值和特征向量的求解。傳統(tǒng)能量法的關鍵是構(gòu)造合適的位移函數(shù)w(x,y),而對于一些邊界條件的假設位移函數(shù)如自由邊界則具有相當?shù)碾y度。本文提出線性表達方法,將邊界約束條件和位移函數(shù)分離,因此基函數(shù)的選擇具有高度自由性。

將邊界約束條件式(9)代入形函數(shù)式(1)中得到

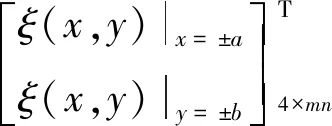
(10)

令

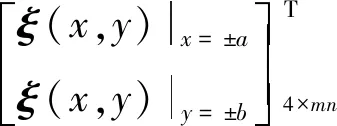
本文采用高斯消元法將約束矩陣轉(zhuǎn)化為階梯型矩陣,得到線性無關的列向量,即獨立的權(quán)重系數(shù)。將未知系數(shù)中的線性相關系數(shù)由線性無關系數(shù)線性表達。

具體過程是,首先對G使用高斯消元法,形成簡化的行階梯形矩陣H。初等行變換不會影響解的結(jié)果,所以Gd=0和Hd=0是等價的。其次采用列變換將H矩陣中每行首個為1的列向量變換到前M列,變換后矩陣為F

F=HIrow

(11)

F=[PQ]

(12)

由于H矩陣的列位置發(fā)生了變換,d向量的行也要進行相應變換,變換后矩陣

γ=Irowd

(13)

得到變換后的向量為γ,將γ向量拆分為兩部分,前M行為α向量,后(mn-M)行為β矩陣。

(14)

因為

Hd=HIrowIrowd=Fγ

(15)

所以Gd=0和Fγ=0是等效的,Gd=0可拆成兩部分相加

P·α+Q·β=0

(16)

因為P矩陣是可逆的,故α可以由β線性表示

α=P-1·Q·β=0

(17)

結(jié)合式(13)、式(14)可得

(18)

式中,I為(mn-M)維的單位矩陣。將式(18)進行變換,便能將d由β表示。

(19)

令

則有

d=Z·β

(20)

將式(16)代入式(8),得到總能量泛函

(21)

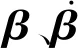
(22)

由于d是與時間相關的未知系數(shù),定義與時間相關的未知系數(shù)β(t)=αeiωt,ω為振動的圓頻率。特征方程可根據(jù)式(19)寫出

(23)

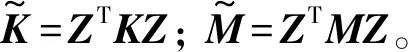
2 收斂性與準確性驗證

本章進行收斂性和精度分析。以鋼材為例,密度ρ=7 850 kg/m3,泊松比μ=0.3,彈性模量E=210 GPa;矩形板長2a=0.5 m,寬2b=0.4 m,圓孔半徑r=0.1 m,厚h=0.005 m。根據(jù)式(3),伸縮因子滿足p≥4,q≥5時解是收斂的。不失一般性,將x、y方向的伸縮因子取相同值,p=q。分析SSSS邊界條件下的固有頻率隨伸縮因子變化關系。

當p=q=1時,低階固有頻率能收斂至解析解,當p=q=5,高階固有頻率也能收斂至解析解,如表1所示。

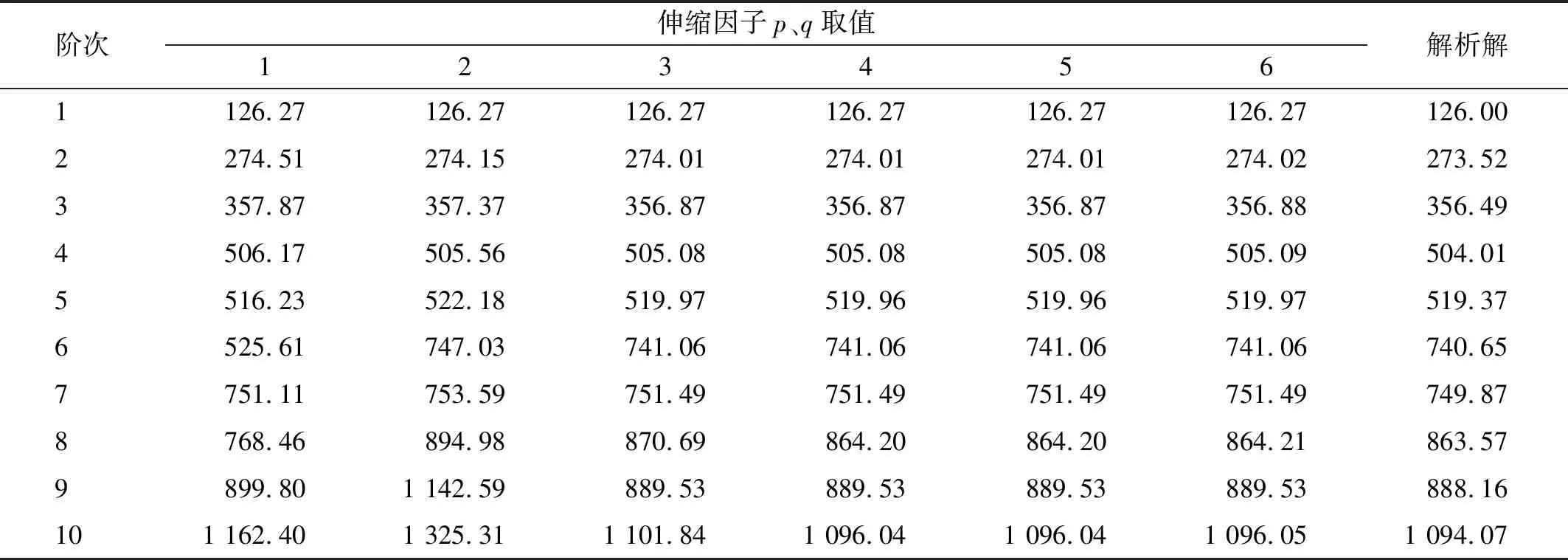
表1 未開口板固有頻率隨伸縮因子變化Tab.1 The natural frequency of an unopened plate varies with the expansion factor 單位:Hz

當p=q=5時,固有頻率達到收斂,證明了式(3)的合理性,如表2所示。

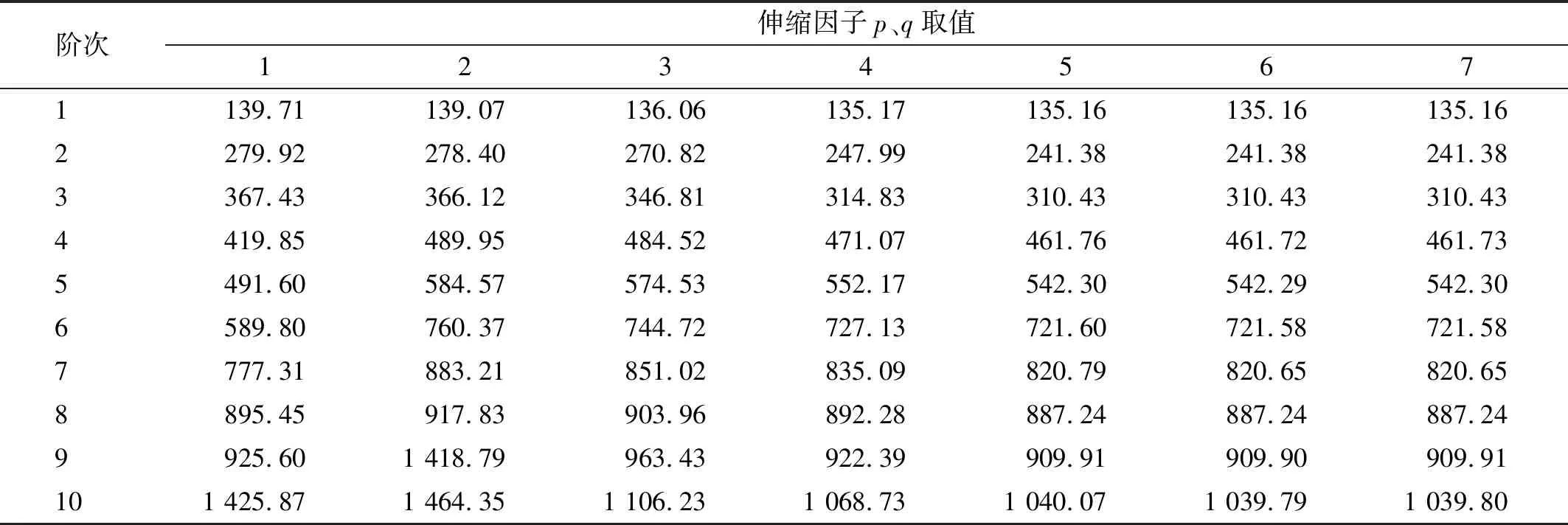
表2 開口板固有頻率隨伸縮因子變化Tab.2 The natural frequency of an open plate varies with the expansion factor 單位:Hz

以SSSS和CCCC邊界條件下的開圓口的矩形板為例,進行準確性驗證。圓形開口半徑為r=0.1 m。將線性表達方法計算結(jié)果與有限元(finite element method,FEM)結(jié)果進行對比。采用的有限元軟件為COMSOL,單元類型為板,結(jié)果如表3和表4所示。誤差計算公式為

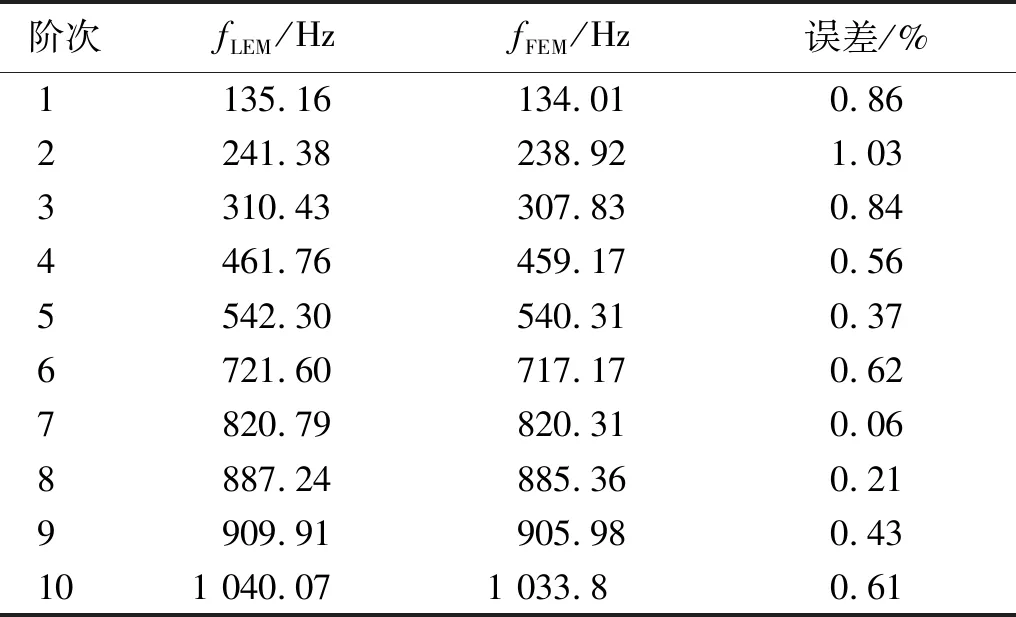
表3 SSSS邊界下開圓口矩形板固有頻率對比

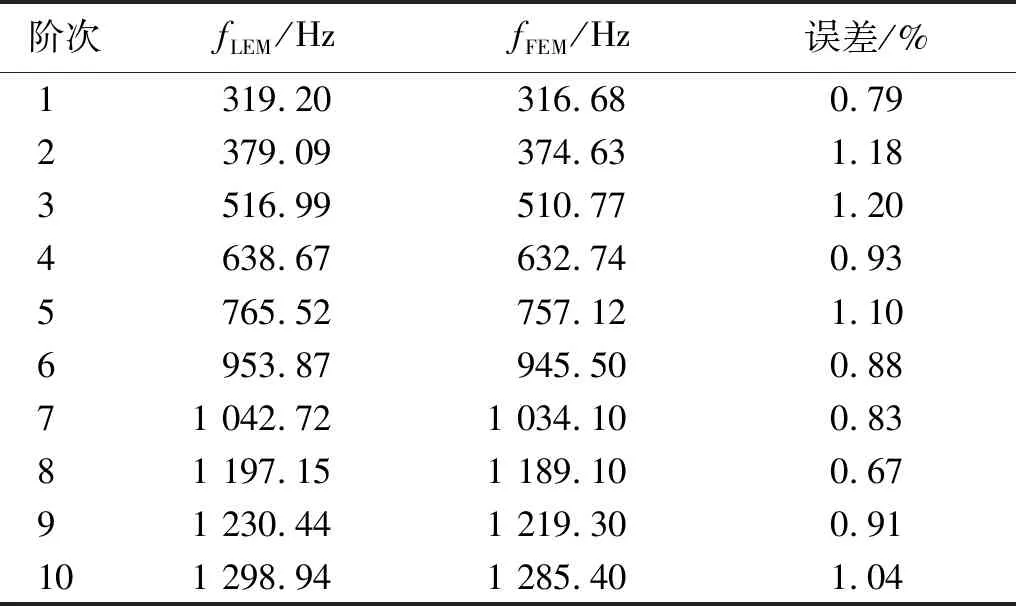
表4 CCCC邊界下開矩形口矩形板固有頻率對比

(24)

式中:fLEM為線性表示方法的結(jié)果;fFEM為有限元計算結(jié)果。

為了驗證振型模態(tài)圖的準確性, SSSS邊界條件下LEM和FEM繪制的模態(tài)圖,如圖4所示。LEM與FEM得到的固有頻率吻合良好,最大誤差不超過2%,見表3、表4。LEM與FEM得到的振型圖基本一致,見圖4。綜合固有頻率和振型圖的對比,說明LEM具有較高的準確性。

圖4 SSSS邊界開矩形口板模態(tài)圖Fig.4 Modal diagram of SSSS boundary plate with rectangular opening

3 開口尺寸對振動性能的影響

為研究開口尺寸對開口板自振特性的影響,采用LEM對不同開口尺寸薄板的自振頻率進行計算,分析開口尺寸對自振頻率的影響規(guī)律。

在CCCC和SFSF邊界條件下,研究開口半徑r與開口板自振頻率f的關系。矩形板長2a=0.5 m,寬2b=0.4 m,厚h=0.005 m;圓孔中心與板中心重合,開口半徑從r=0(無開口),0.005 m、0.010 m、0.001 5 m、…、0.150 m。最大開口半徑為0.15 m,當開口尺寸繼續(xù)增大,薄板理論不再適用。將開口半徑與固有頻率關系繪制成圖,如圖5所示。

圖5 不同邊界下開口半徑與固有頻率關系Fig.5 Relationship between opening radius and natural frequency under different boundaries

由圖5可知,當開口尺寸較小時,開口對各階固有頻率的影響較小。可能的解釋是,固有頻率和結(jié)構(gòu)的動能和應變能有關,其中動能與結(jié)構(gòu)的質(zhì)量和速度相關,應變能與結(jié)構(gòu)剛度有關。當開口較小時,對質(zhì)量和剛度影響都較小,所以對固有頻率的影響較小。小開口板的頻率和模態(tài)可近似為未開口板進行分析。

在CCCC邊界條件下,1階固有頻率隨著開口尺寸增大而增大,2階、3階、4階固有頻率隨著開口增大先減小后增大,見圖5(a)。根據(jù)未開口矩形板振型圖6,可能的解釋是,在1階振型中,中心開口位于振動峰谷位置,開口對動能影響比應對變能影響大,從而導致1階固有頻率隨著開口尺寸增大而增大。2階、3階、4階振型中,中心開口位于節(jié)線位置,開口對動能影響比應對變能影響小;隨著開口尺寸增大,逐漸接近峰谷位置,對動能影響比應對變能影響大,從而導致固有頻率隨著開口增大先減小后增大。

在SFSF邊界條件下,1～4階固有頻率隨著開口增大而減小,見圖5(b)。根據(jù)未開口矩形板振型圖7,并與CCCC邊界條件下進行對比,可能的解釋是:1階振型中,振動峰谷為一帶狀區(qū)域,不完全集中在中心位置,中心開口對動能影響比應對變能影響小;SFSF邊界下整體剛度比CCCC邊界下小,隨著開口增大,對動能影響一直比應對變能影響小,沒有出現(xiàn)CCCC邊界下固有頻率隨著開口增大先減小后增大現(xiàn)象。

4 開口形狀對振動性能的影響

為研究開口形狀對自振特性的影響。采用LEM對不同開口形狀薄板的自振頻率進行計算,分析開口形狀對自振頻率的影響規(guī)律。

在CCCC和SSSS邊界條件下,矩形板長2a=0.5 m,寬2b=0.4 m,厚h=0.005 m,開口面積s=0.02 m2,矩形孔長寬比a′/b′=ka,橢圓孔長軸與短軸比r1/r2=kr。不同長寬比ka、長短軸比kr與自振頻率關系如圖8、圖9所示。

圖8 CCCC邊界下長短軸比kr與自振頻率關系Fig.8 Relationship between the long to short axis ratio kr and natural frequency under CCCC boundary

圖9 SSSS邊界下長寬比ka與自振頻率關系Fig.9 Relationship between aspect ratio ka and natural frequency under SSSS boundary

由圖8、圖9可知,在邊界條件和開口面積相同情況下,開口形狀對1階、4階自振頻率影響較小(為1%～3%),對2階、3階影響較大(為8%～20%)。根據(jù)未開口矩形板振型圖6,可能的解釋是:1階、4階峰谷沿x軸和y軸對稱,開口長邊方向x軸和沿y軸對薄板的動能影響較接近;而2階、3階峰谷只沿y軸或只沿x對稱,開口長邊方向?qū)幽艿挠绊懖町愝^大。

隨著長寬比ka、長短軸比kr從0.5增大到2.0,1階自振頻率先增大后減小,2階頻率逐漸減小,3階頻率逐漸增大。可能原因是,當開口接近峰谷時自振頻率增加,開口遠離峰谷時自振頻率減小。

5 多開口自振頻率計算

以不同開口數(shù)量的矩形板為例,與有限元結(jié)果對比,驗證LEM計算多開口板時的準確性。單元矩形板長0.5 m,寬0.4 m,厚0.005 m,圓孔半徑0.05 m。開兩孔模型如圖10(a)所示,圓孔中心坐標為(±0.125,0);開四孔模型如圖10(b)所示,圓孔中心坐標為(±0.125,±0.10);計算結(jié)果如表5和表6所示。

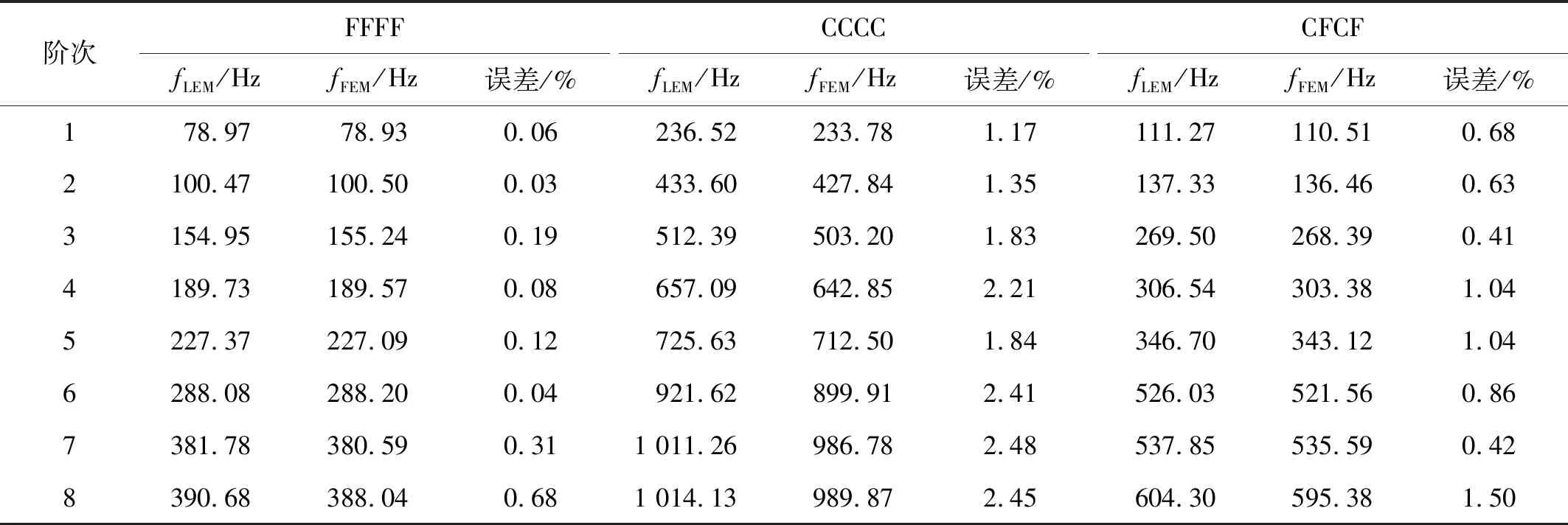
表5 不同邊界下開兩圓孔矩形板固有頻率Tab.5 Natural frequencies of rectangular plates with 2 circular holes under different boundaries

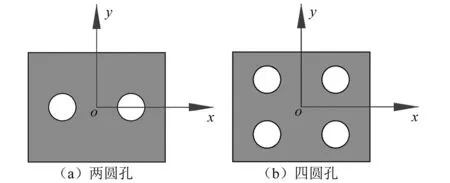
圖10 多開口矩形板示意圖Fig.10 Schematic diagram of multi opening rectangular plate

由表5、表6可知:在不同邊界條件下,低階固有頻率誤差基本在1%以內(nèi);在CCCC邊界下,高階固有頻率最大誤差小于2.5%,高階固有頻率誤差大于低階誤差[31]。LEM在計算多開口矩形板自振頻率準確可靠。

6 結(jié) 論

基于能量法原理,采用高斯小波函數(shù)作為位移函數(shù),提出利用線性表達方法(LEM)處理邊界條件,解耦了邊界條件與位移形函數(shù)。首先以四邊簡支條件下開圓口薄板為例驗證了LEM的收斂性和準確性,然后分析不同開口尺寸和不同開口形狀下開口薄板的自振頻率,最后分析了多開口矩形板自振頻率。通過本文的研究,得到如下結(jié)論:

(1) 高斯小波函數(shù)中伸縮因子的取值與解的收斂性相關,當函數(shù)支撐范圍小于板的邊長時才能保證解收斂。

(2) 采用線性表達方法的不同邊界條件下單開口、多開口振動計算結(jié)果與有限元計算結(jié)果吻合較好。

(3) 當開口尺寸較小時,開口對固有頻率的影響較小,小開口板的頻率和模態(tài)可近似為未開口板進行分析。開口對各階自振頻率影響程度隨著模態(tài)圖的峰谷位置變化。

(4) 在邊界條件和開口面積相同情況下,隨著開口形狀與模態(tài)圖中峰谷重合范圍的不同,自振頻率產(chǎn)生不同影響。