非堆積型多顆粒阻尼器等效力學模型及其減振性能分析
李小軍, 田超杰, 黃緒宏
(1. 北京工業大學 城市與工程安全減災教育部重點實驗室,北京 100124;2. 青島理工大學 土木工程學院,山東 青島 266520)
作為一種無源的被動控制裝置,顆粒阻尼技術最早起源于航空及機械振動控制領域,其通過將多個金屬或非金屬顆粒材料按某一填充率放入受控結構的特定空腔內進行構造。當結構發生振動時,通過顆粒之間及顆粒與容器之間碰撞、摩擦,消耗、存儲并傳遞振動能量,以此達到結構減振控制的目的。因其具有減振效果好、作用頻帶寬、造價低廉等優點,有望在工程結構振動控制領域中得到較好的應用。
雖然顆粒阻尼技術具有較好的應用前景,然而對其復雜的非線性特性認識不足限制了其在實際工程結構中的推廣應用,深入揭示其減振性能及影響因素成為研究的關鍵。Papalou等[1-2]設計進行了簡諧激勵及隨機振動下顆粒大小、附加質量比、容器尺寸及外部激勵強度對減振性能影響的振動臺試驗。研究結果表明,相較于單顆粒沖擊阻尼器,多顆粒形式明顯降低了噪音,并改善了阻尼器減振效果受外部激勵影響的魯棒性。閆維明等[3-5]系統分析了多顆粒阻尼器 (multi-particle damper, M-PD)物理參數對振動控制效果的影響規律,并對其在多層框架結構、多跨連續橋梁及沉管隧道中的應用進行了探索。通過試驗研究,其進一步指出M-PD在土木工程領域宜采用非堆積形態進行構造,即非堆積型多顆粒阻尼器(non-packed particle damper, NPPD)。Papalou等[6]通過開展大理石柱縮尺模型振動臺試驗,討論了附加質量比、阻尼器布置位置、顆粒大小等參數對M-PD減震性能的影響。魯正等[7-8]對附加緩沖材料的M-PD減震性能進行了討論,并與懸吊式調諧質量阻尼器減震性能進行對比,試驗結果表明,同等條件下M-PD的減震性能優于懸吊式調諧質量阻尼器。Fu等[9-10]進行了不同顆粒級配下M-PD減振效果試驗研究,并與調諧液體質量阻尼器進行對比,結果顯示顆粒阻尼器作用頻帶寬度更廣。上述試驗研究初步探明了M-PD減振性能及機理,為數值分析及相關研究提供了試驗數據及支撐。
在試驗基礎上,開展力學模型研究,進行數值仿真分析是進一步明確M-PD減振性能的重要手段。Yao等[11]采用近似線性化的方式將豎向激勵下調諧型顆粒阻尼器等效為豎向雙重調諧質量阻尼器,并對該力學模型進行了試驗驗證,結果表明該力學模型能夠合理預測阻尼器減振性能。許維炳等將調諧型顆粒阻尼器等效為雙重調諧質量阻尼器,并基于該模型進行了參數分析及阻尼器優化設計,優化后阻尼器被應用到多跨連續橋梁當中。上述采用近似線性化所建立的等效力學模型一定程度上反映了M-PD減振性能,但其并不能較好地反映顆粒群與結構碰撞過程中的非線性特性,為此部分學者引入碰撞間距建立對應力學模型。基于等效前后質量及空隙率相等且材料特性及形狀不發生變化的原則,魯正等[12]基于接觸單元法將M-PD等效為單顆粒力學模型,在隨機激勵下討論了碰撞間距、附加質量比及碰撞阻尼系數等對減振性能的影響規律。采用相似的等效原則,Yan等[13]通過引入碰撞恢復系數考慮顆粒群與容器之間的碰撞效應,建立應對的力學模型,并基于該模型進行了參數影響分析及耗能機理分析。黃緒宏等[14]在上述等效單顆粒力學模型研究基礎上,進一步引入慣容元件,考慮顆粒群滾動對M-PD減振效果的影響,建立了考慮慣容的等效單顆粒模型(equivalent inertia single-particle model, EISM),并基于EISM進行了自由振動、簡諧激勵及地震作用下減振效果分析及能量變化規律分析。
上述考慮碰撞效應所建立的力學模型進一步明晰了M-PD非線性特性,然而目前所建立的力學模型仍然存在不足之處,包括基于碰撞恢復系數所建立的力學模型并不能反映顆粒群與結構碰撞時的時間效應,且現有商業有限元軟件尚未給出與其對應的數值仿真分析方法,限制了該模型的應用;基于接觸單元法建立的力學模型并不完善,尚未考慮顆粒群的慣容屬性,且其物理參數取值原則并未明確。
為進一步揭示M-PD的減振機理和性能特征,本文以NPPD作為研究對象,在現有EISM研究基礎上,建立基于接觸單元法的等效慣性單顆粒力學模型(equivalent inertia single-particle model based on contact element method, EISM-CE),并基于Runge-Kutta算法給出對應數值仿真分析流程。設計進行NPPD-單層鋼框架模型振動臺試驗,提出對應EISM-CE的參數取值原則,并進行等效模型試驗驗證及對比分析。最后,在最優填充率下對比分析NPPD減振性能及能量變化規律。
1 基于接觸單元法的等效單顆粒模型
1.1 等效單顆粒模型的提出
假設運動過程中顆粒群集中排布,考慮非碰撞階段顆粒群滾動及其他非線性特性對NPPD(如圖1所示)減振性能的影響,黃緒宏等引入慣容元件建立對應EISM,見圖1(b)。其中:q為慣容系數,q越大,表明顆粒群與結構之間越難發生相對運動;d為顆粒群等效集中質量m1與結構之間的碰撞間距;e為碰撞恢復系數。
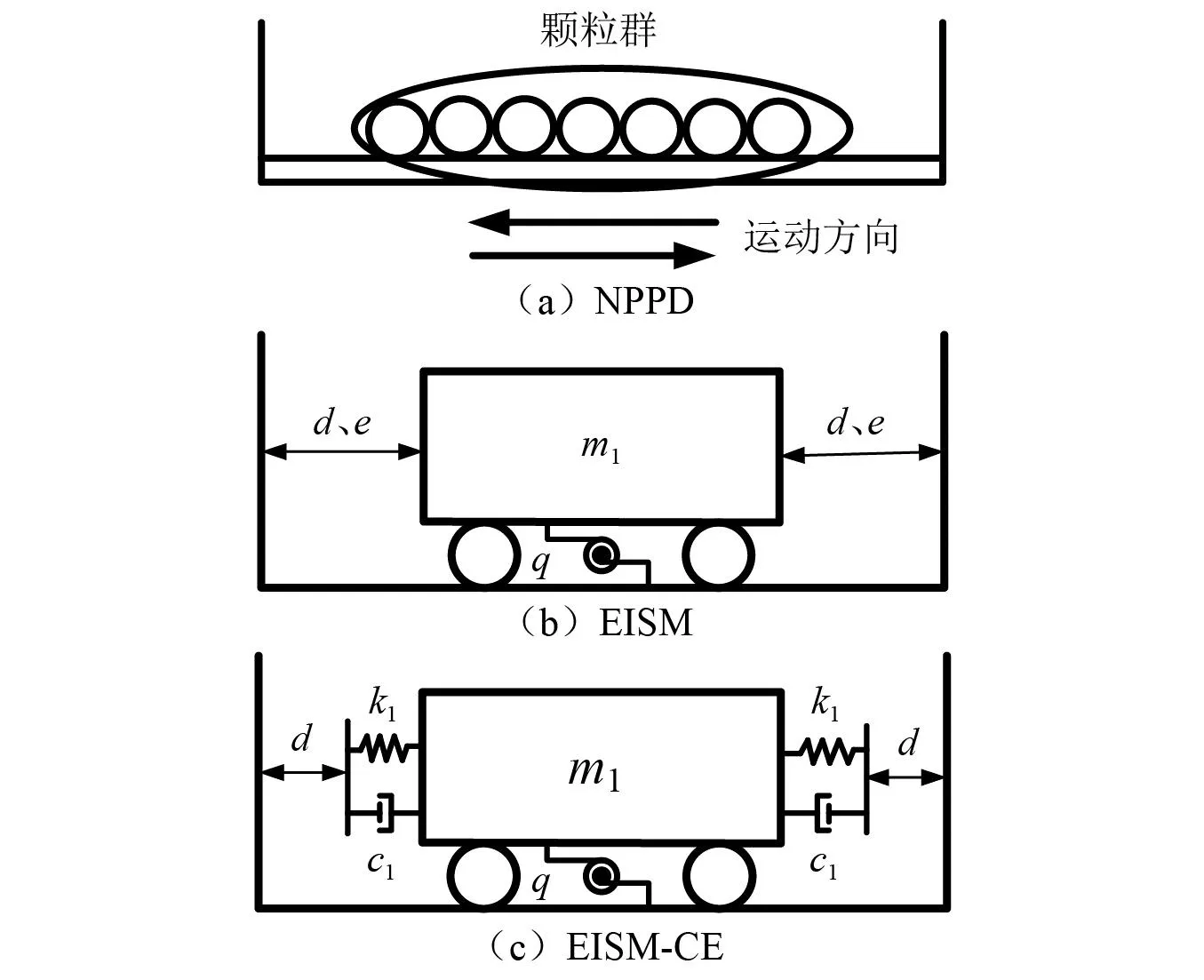
圖1 等效單顆粒力學模型Fig.1 Equivalent single particle model
為進一步考慮碰撞過程中的時間效應,在EISM研究基礎上,本文基于接觸單元法提出對應EISM-CE模型,見圖1(c)。與EISM相比,EISM-CE通過等效碰撞剛度k1及等效碰撞阻尼c1考慮碰撞過程中的顆粒群與結構之間的相互作用,其中k1反映碰撞過程中顆粒群與容器之間動量交換的能力,c1反映碰撞過程顆粒群與容器之間碰撞、摩擦所具有的耗能能力。
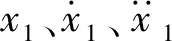
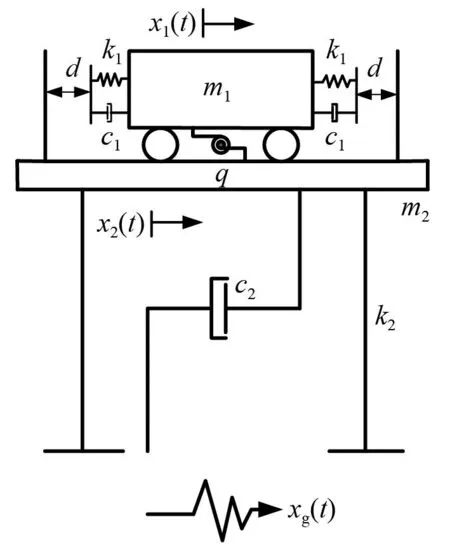
圖2 單自由度EISM-CEFig.2 Single degree of freedom EISM-CE
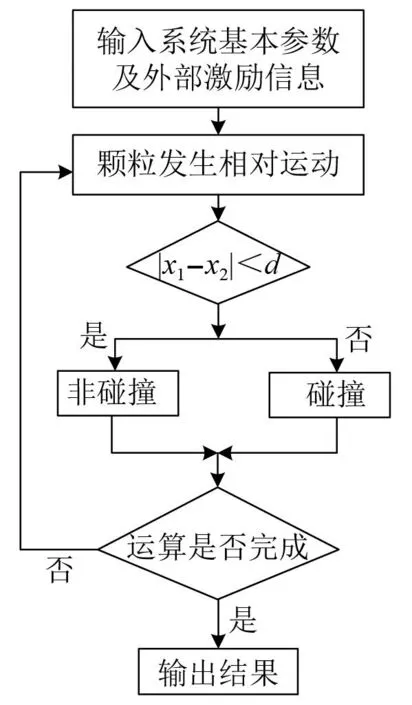
圖3 數值仿真流程Fig.3 Flow chart of simulation
1.2 未碰撞階段體系運動方程
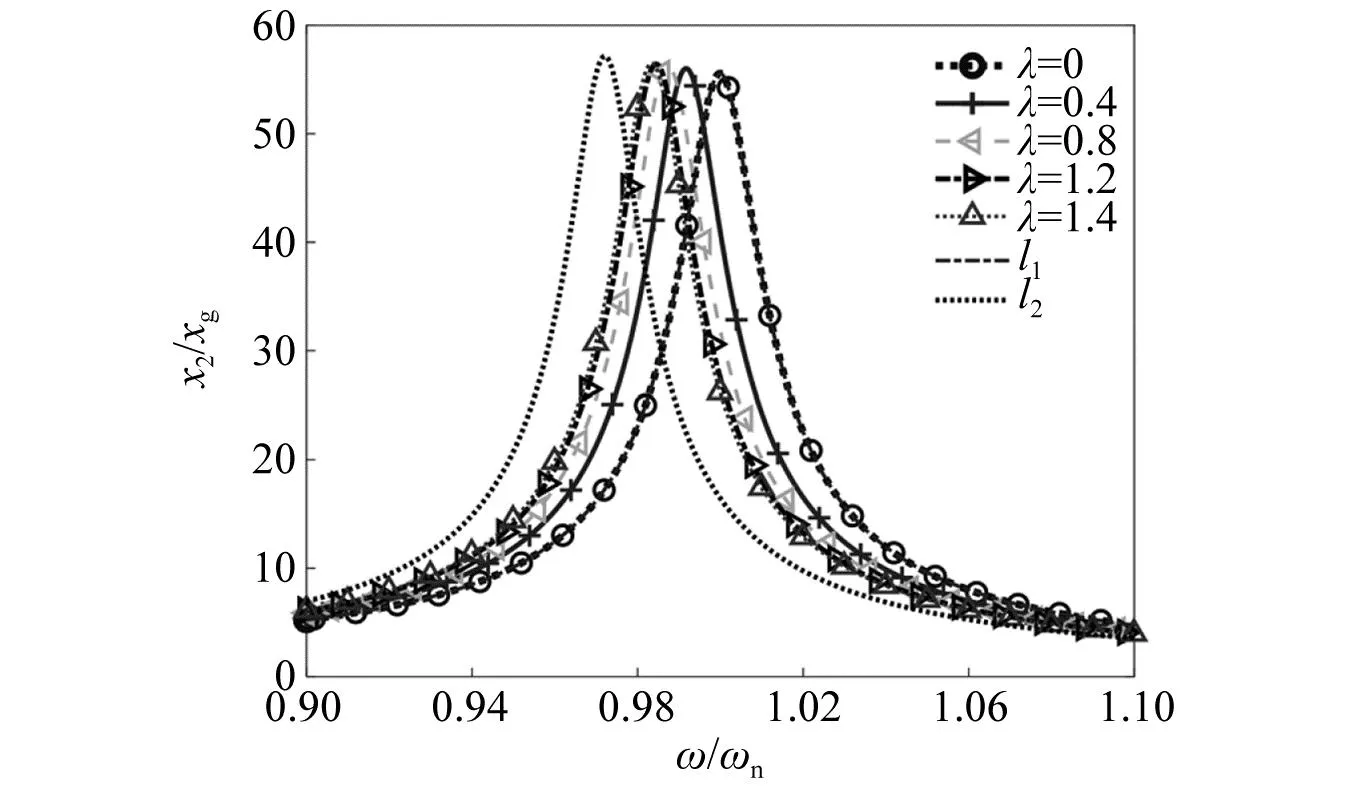
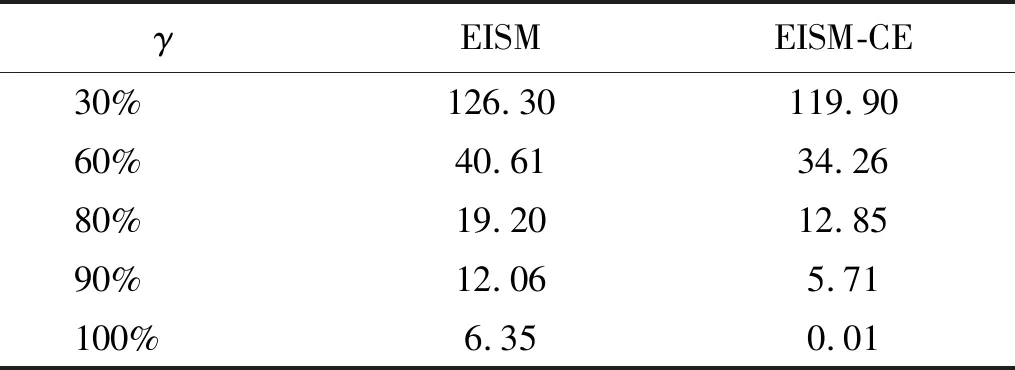
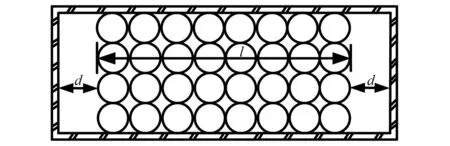
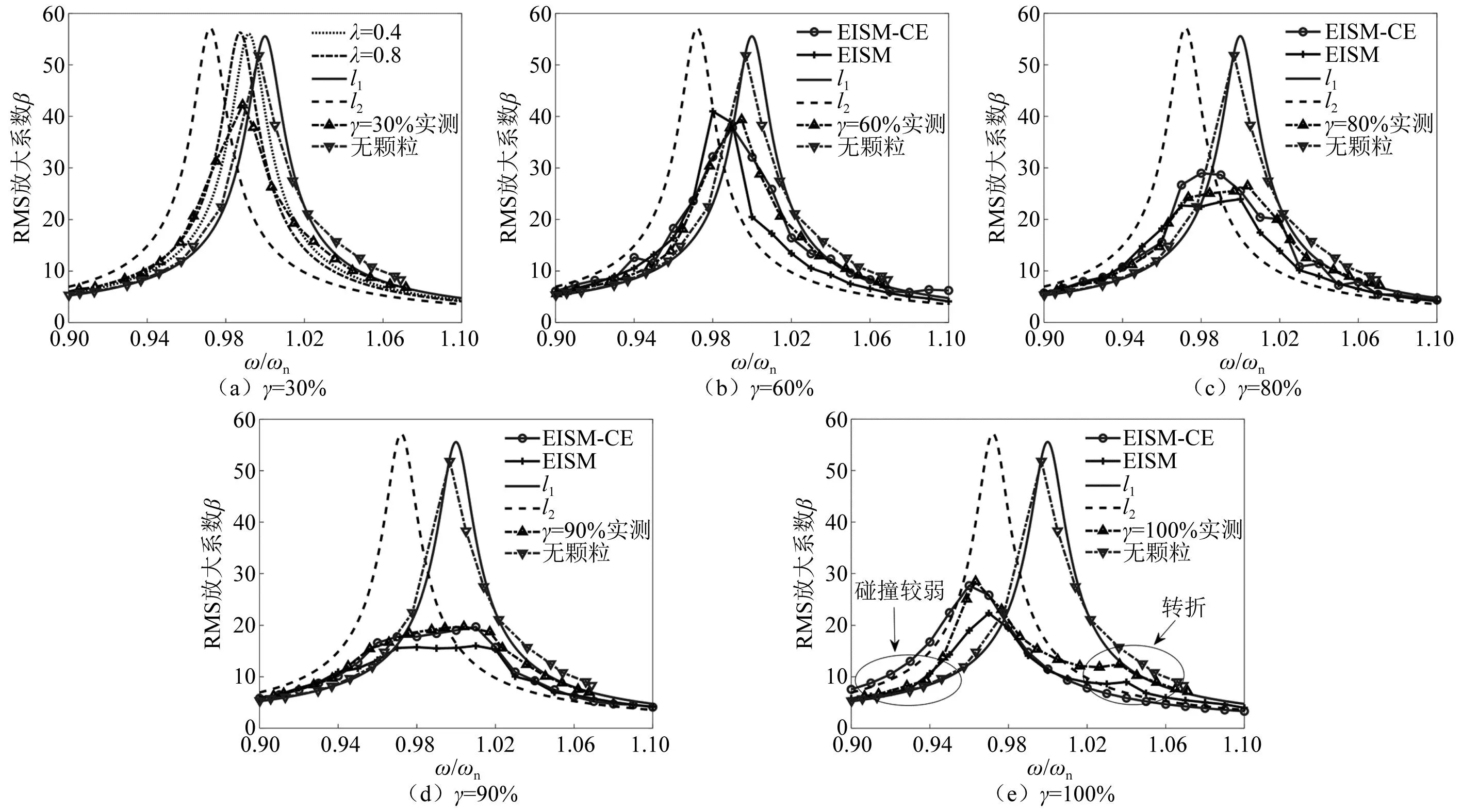
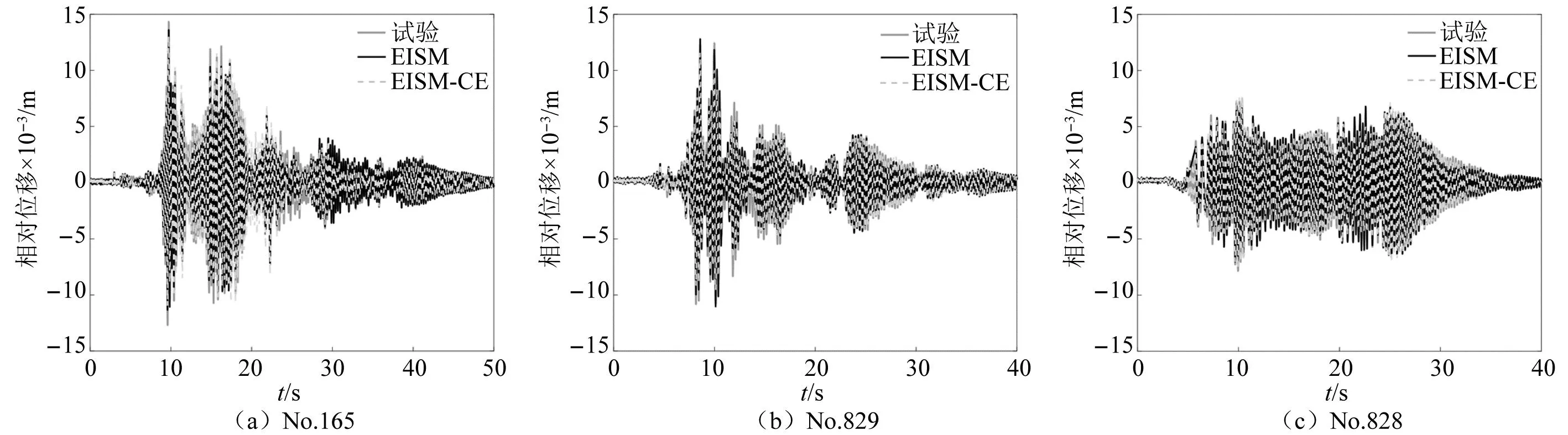
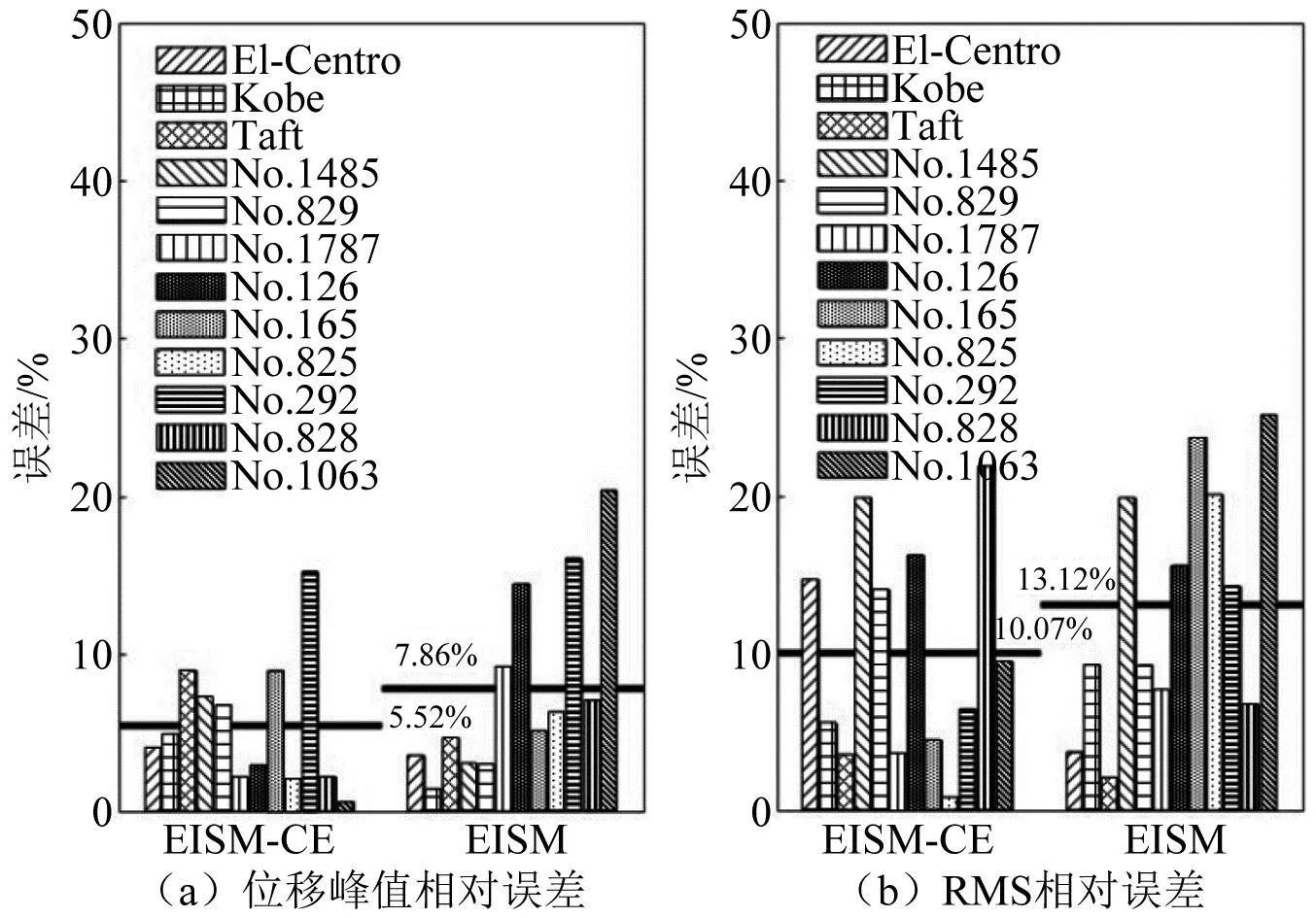
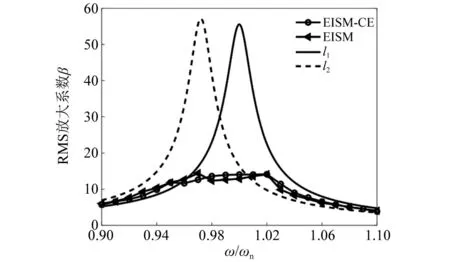
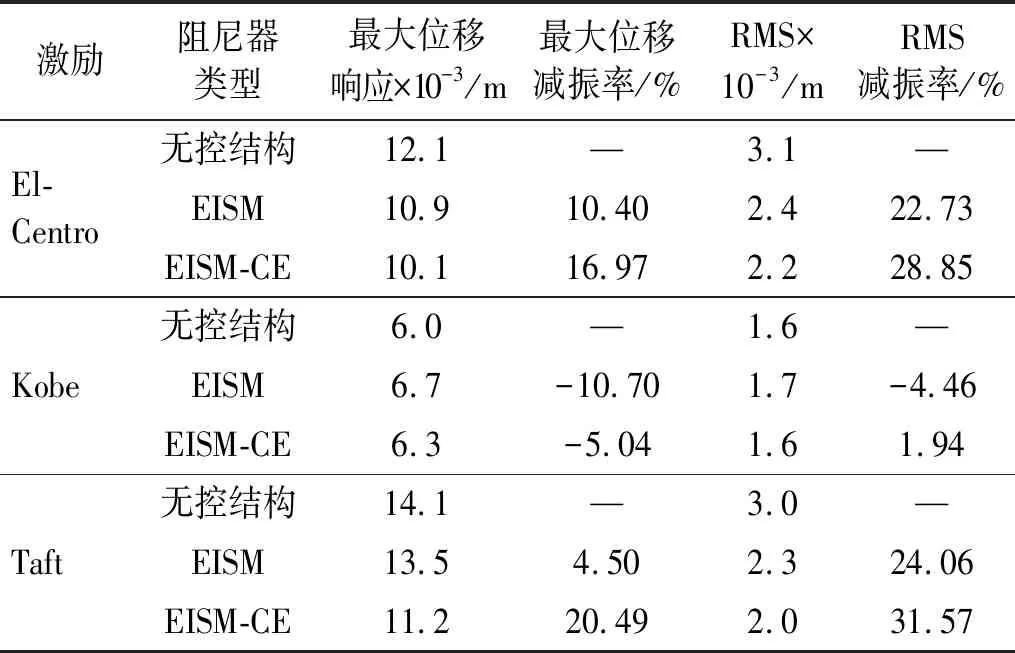
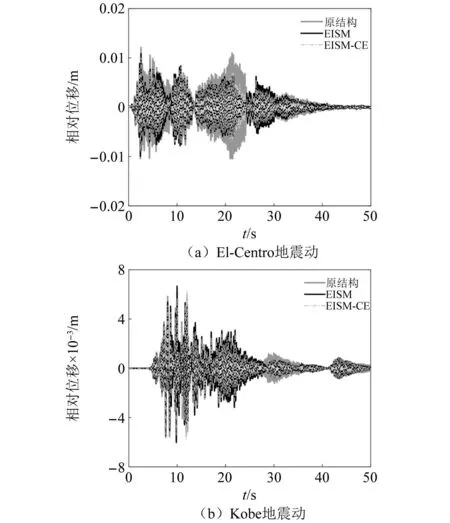
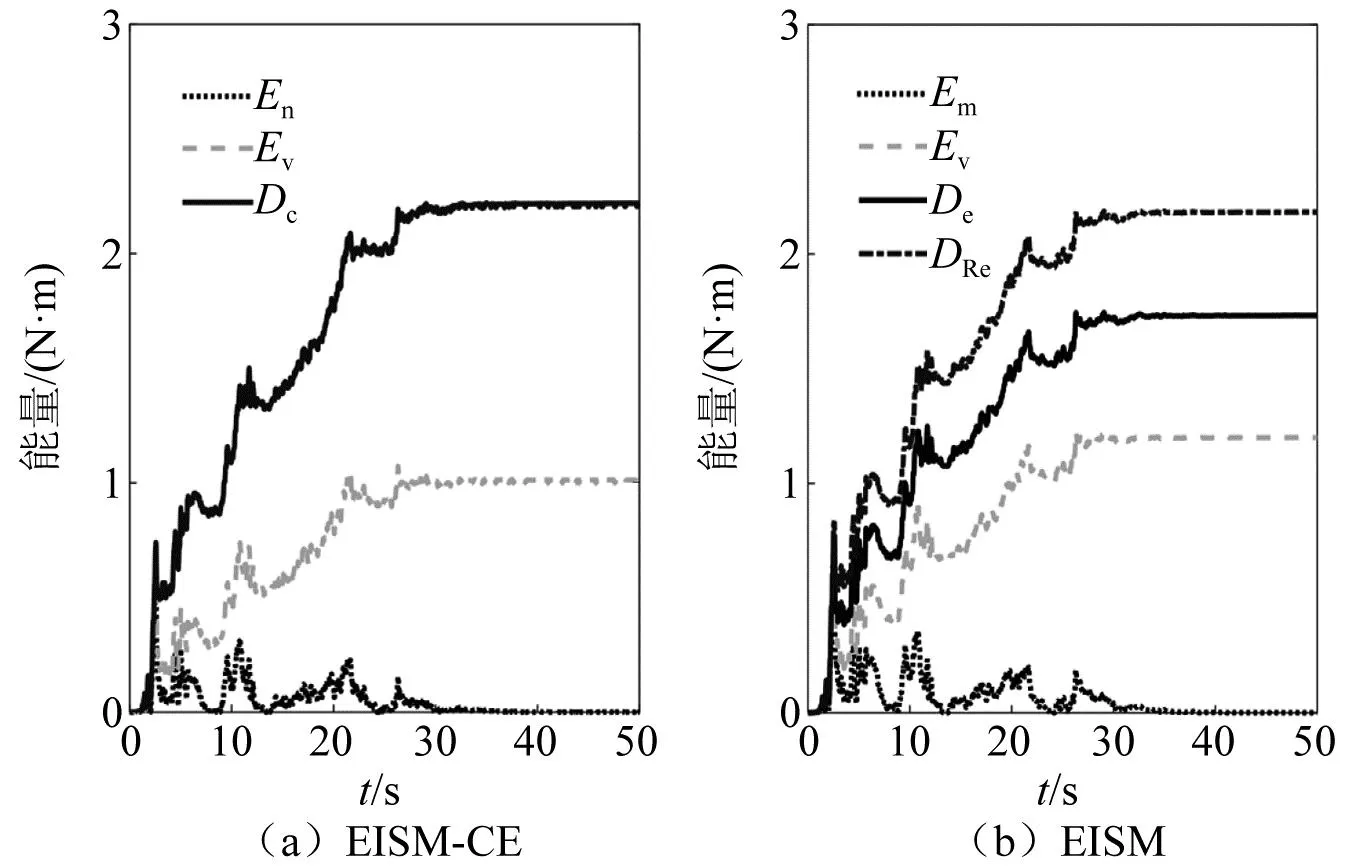
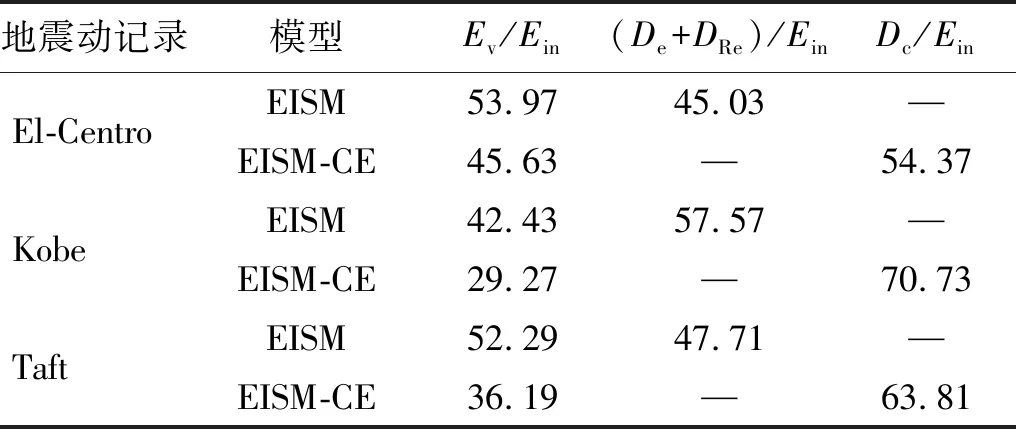
當阻尼顆粒與結構未發生碰撞時時(|x1-x2| (1) 進行拉普拉斯變換可得結構響應放大系數 (2) (3) 取μ=5.8%,λ對結構絕對位移放大系數頻響曲線的影響如圖4所示。圖4中:l1對應原結構位移放大頻響曲線;l2對應附加質量比5.8%所對應的位移放大頻響曲線。由圖4可知,隨著λ的增加,結構位移放大系數頻響曲線逐漸向較低頻率移動,且受λ增加影響的靈敏度逐漸降低。當λ趨于無窮大時,位移放大系數頻響曲線與l2重合,此時認為顆粒與結構同為一體,不發生相對滾動。 圖4 結構位移頻響曲線Fig.4 Frequency response curve of structural displacement 結構碰撞是一種高度復雜的非線性過程。本文采用接觸單元法模擬顆粒與容器壁之間的碰撞過程,當沖擊質量塊m1與結構m2發生碰撞后(|x1-x2|≥d),由D’Alembert可得 (4) 式中, sign(·)為符號函數,其滿足 (5) 為驗證力學模型的合理性,清晰NPPD減振性能,本文設計進行NPPD-單層鋼框架模型振動臺試驗,試驗裝置布置如圖5所示。振動臺的各項性能參數指標如表1所示。結合振動臺臺面尺寸,并考慮假定的結構基本自振周期需求,本試驗設計框架頂部鋼板尺寸為500 mm×500 mm×5 mm;柱高為800 mm,橫截面尺寸為50 mm×5 mm,并沿柱高包裹高聚合物材料以提高框架阻尼比;頂板上放置顆粒腔體,腔體與頂板采用8 mm螺栓進行固接,腔體垂直于振動方向寬為300 mm,沿振動長度設置滑道以調節兩側碰撞板的間距,進而控制顆粒填充率。實測鋼框架質量為17.2 kg,結構基本頻率ω0=3.75 Hz,結構附加阻尼比為0.9%。試驗中,阻尼顆粒取直徑8 mm鋼珠,μ=5.8%,依次進行簡諧激勵及地震動作用下的振動臺試驗研究。 圖5 振動臺與試驗結構模型Fig.5 Shaking table and test structure model 基于等效前后質量相等,材料及形狀保持一致的原則,Papalou等[15-16]提出M-PD對應等效單顆粒力學模型的等效原則,然而該種等效方法可能并不適應于NPPD。為此黃緒宏等依據顆粒等邊三角形排列的形式計算兩側碰撞間距。為充分考慮顆粒群碰撞過程中的時間效應,借鑒上述等效原則,假設顆粒群按照四邊形集中排布如圖6所示,計算兩側d。圖6中,l為集中排布后顆粒群長度。以本文對應的NPPD為例,不同填充率γ對應d取值如表2所示,其中γ取顆粒有序正方形排列投影面積與容器底面積之比。 表2 d取值Tab.2 Parameter values of d 單位:mm 圖6 顆粒排布規則Fig.6 Particle arrangement rules 參考EISM,本文引入慣容元件考慮非碰撞階段顆粒群滾動及其他非線性特性對NPPD減振性能的影響。由圖4可知,λ對顆粒群運動過程中的非碰撞階段影響顯著,因此可以通過對比非碰撞階段頻響曲線確定λ值。當不考慮γ對λ的影響時,可近似通過低填充率下NPPD-SODF位移放大系數頻響曲線確定λ的取值。 EISM-CE中k1及c1對NPPD減振性能具有顯著的影響。k1能夠近似反映碰撞過程中顆粒群與結構之間動量交換的能力,然而由于多顆粒復雜的非線性特性,目前仍未見k1詳細的理論推導。在試驗研究基礎上,Huang等[17]提出了等效連體顆粒質量模型,并給出當γ=100%時兩個非堆積顆粒群碰撞對應力學模型中等效連接剛度k0的取值 (6) 式中:μm2/(many)為沿振動方向顆粒群的排數;ma為單顆粒的質量,ma=4/3πr3ρa,r為顆粒半徑;ε為孔隙率,對于四邊形排布,取ε=0.365;w2為對應容器寬度的正方形面積;ny為單排顆粒數量,ny=w/(2r);ρa為顆粒材料密度。在k0基礎上,為進一步考慮顆粒群排布及碰撞規則等對k1的影響,引入顆粒群碰撞形式修正系數ψ,對應k1計算公式為 k1=ψk0 (7) c1體現了顆粒與結構之間碰撞及摩擦耗能能力,其主要與顆粒碰撞恢復系數相關。在現有e經驗取值基礎上[18],考慮顆粒群排列形式對耗能能力的影響,取顆粒群對應e=0.2。由e與顆粒碰撞附加阻尼比ξ1的經驗公式式(8)[19]及ξ1與c1的關系式式(9)可得到k1對應的c1。 (8) (9) 設計進行簡諧激勵下振動臺試驗研究,試驗激勵幅值取0.03g,調整兩側碰撞板間距依次進行30%、60%、80%、90%和100%填充率下減振效果分析。拾取不同激勵頻率下結構及振動臺臺面的位移響應,計算均方根(root mean square, RMS)(SRM)位移及位移均方根放大系數β作為減振效果指標,計算公式為 (10) (11) 式中:xi為第i個時間步的位移響應;N為時間步數,上標“s”和“t”分別為結構和振動臺臺面的位移響應。30%~100%填充率下結構位移響應均方根放大系數隨激振頻率比變化規律如圖7所示。 圖7 γ對減振效果影響分析Fig.7 The influence of γ on vibration reduction effect 由圖7中試驗結果分析可知: (1) 在當前試驗參數設置下,當γ=90%時,減振效果最優,且減振作用頻率范圍較大。 (2) 當γ=30%時,由于碰撞間距較大,運動過程中,顆粒與容器壁基本不發生碰撞,無法發揮耗能能力,因此減振效果較差。頻響曲線對比結果顯示,由于顆粒群慣容屬性的影響,與原結構頻響曲線相比,γ=30%對應頻響曲線明顯位于較低頻側。 (3) 當γ<90%時,隨著γ的增加,碰撞間距逐漸減小,顆粒與容器壁的碰撞次數逐漸增加,耗能能力逐漸增強,因此減振效果逐漸增加。當γ>90%時,隨著γ的進一步增加,碰撞間距逐漸縮小,減振性能逐漸降低。在這一過程中,雖然顆粒與容器壁的碰撞次數逐漸增加,但沖擊過程中碰撞間距減小,導致沖擊力減小,顆粒群無法充分發揮耗能能力,致使NPPD減振效果降低。 為驗證EISM-CE的有效性,進行試驗驗證,并與EISM進行對比分析。為此,首先確定λ的取值。由30%填充率對應頻響曲線實測值(見圖7(a))及理論解(式(2))可得λ=0.8,對應曲線相關系數R2= 0.969。在此基礎上,考慮顆粒群排布規則對k1的影響,結合γ=100%對應頻響曲線,基于數值仿真確定ψ=5,對應k1=1 712 N/m,c1=36.67 N·s/m。基于上述參數取值,假設顆粒群初始位于容器一側進行數值仿真分析,對應不同γ下頻響曲線擬合及實測對比如圖7所示,分析結果表明: (1) 基于碰撞恢復系數所建立的EISM及本文提出的EISM-CE均能夠較好地模擬NPPD減振性能,且EISM-CE擬合結果更加理想。 (2) 基于EISM-CE的減振機理分析結果表明,當γ<90%時,隨著d的減小,等效沖擊質量m1與結構之間的碰撞次數及劇烈程度逐漸增加,碰撞耗能逐漸增加,對應減振性能逐漸增加。當γ>90%時,隨著d的減小,雖然碰撞次數逐漸增加,但碰撞劇烈程度逐漸降低,碰撞耗能逐漸減小,m1逐漸趨向于周期多次碰撞狀態,對應減振性能逐漸降低。當γ=90%時,對應最優的減振性能。 (3) 力學模型詳細對比分析結果表明,當γ=60%或γ=80%,ω/ωn較大時,EISM-CE與EISM擬合結果存在一定差異。EISM-CE擬合結果更加理想。究其原因,當激勵幅值保持不變時,ω/ωn越大結構位移及速度越小,此時顆粒群碰撞的時間效應影響越顯著。由于EISM未考慮時間效應,顆粒群與結構的碰撞次數增加,減振性能增加,位移放大系數曲線位于實測頻響曲線下側。相比之下,EISM-CE考慮了碰撞時間效應,擬合結果更加理想。 (4) 當γ=100%,β較小時,基于EISM-CE得到的頻響曲線與實測曲線存在一定的差異。具體分析表明,當γ=100%時,運動過程中實際顆粒群排布較為密集,兩側存在一定的碰撞間距。當β較小時,顆粒群并未與結構之間充分碰撞,此時實測頻響曲線更加趨向于l1。而對于EISM-CE而言,當γ=100%時,此時已存在明顯的相互作用,這導致頻響曲線模擬值與實測值存在一定誤差。相比之下,由于EISM考慮了初始碰撞間距的影響,因此當β較小時EISM更加理想。需要注意的是,當ω/ωn=1.04左右時,此時實測頻響曲線及EISM對應頻響曲線存在轉折現象,這亦是由于碰撞間距引起減振性能非線性所導致的。 地震激勵具有復雜的頻譜特性,在其作用下開展相關研究對于進一步認清力學模型的合理性具有重要意義。為此,選取γ=90%對應的NPPD,設計進行了地震作用下NPPD-單層鋼框架振動臺試驗。考慮到顆粒阻尼器作用力特性及前期經驗,除選取3條經典地震動記錄(El-Centro地震動記錄、Taft地震動記錄和Kobe地震動記錄)作為振動臺輸入外,另外參考ATC-63 project所記錄的地震動記錄,選取3條遠場地震動記錄(No.1485、No.829和No.1787),3條近場無速度脈沖地震動記錄(No.126、No.165和No.825)和3條近場有速度脈沖地震動記錄(No.292、No.828和No.1063)作為振動臺輸入,調整峰值加速度為0.20g進行振動臺試驗。3條不同類型地震動記錄對應的結構實測及模擬位移曲線,如圖8所示。EISM-CE模型和EISM模型對應位移峰值相對誤差和RMS相對誤差對比分析結果,如圖9所示。 圖8 地震作用等效模型試驗驗證Fig.8 Test verification of equivalent model under seismic excitation 圖9 擬合結果誤差統計Fig.9 Error statistics of fitting results 綜合分析可知,EISM-CE擬合結果更加理想,其中EISM-CE的位移峰值相對誤差為5.52%,RMS相對誤差為10.07%。EISM的位移峰值相對誤差為7.86%,RMS相對誤差為13.12%。 以NPPD-鋼框架模型作為研究背景,基于EISM-CE,進行減振性能對比分析,并結合能量發展討論其作用機理。選取最優參數對應的NPPD作為研究對象。當激勵幅值為0.03g時,對應EISM-CE的最優碰撞間距d0=4 mm。同一NPPD對應EISM參數為d=10.4 mm,e=0.25。最優NPPD參數設置下本文提出的EISM-CE及EISM對應β頻響曲線如圖10所示。由圖10可知,2條頻響曲線較為接近,這進一步說明了力學模型的合理性。在最優參數取值基礎上,依次進行自由振動、簡諧激勵及地震動作用下的能量分析及減振效果分析。 圖10 位移放大系數頻響曲線Fig.10 Frequency response curve of β 初始結構位移取0.05 m,在最優碰撞間距下進行自由振動減振性能分析,如圖11所示。由圖11可知,自由振動下NPPD具有較好的減振效果,結構位移峰值呈非線性衰減。在振動初期,衰減速度較快,在中后期,衰減速度較慢。不同力學模型減振性能對比分析結果表明,振動前期EISM-CE結構位移峰值衰減速度更快,但到中后期,EISM的結構位移峰值衰減速度相對較快。原因分析表明,碰撞前期結構運動較劇烈,由于EISM-CE考慮了碰撞過程中的時間效應,系統耗能能力更加顯著。中期后,EISM-CE中線性剛度k1與c1一定程度上限制了m1相對運動,因此耗能能力略有衰減。相比之下,中期后EISM中m1運動相對較為劇烈,因此耗能能力略微優于EISM-CE。 圖11 自由振動下減振效果分析Fig.11 Analysis of vibration reduction effect under free vibration 為進一步分析系統能量耗散過程,基于運動方程建立系統能量方程,并與EISM進行對比分析。假設EISM-CE-SDOF與EISM-SDOF對應的外部輸入能量分別為E1和E2,則系統能量分別滿足式(12)和式(13)。 E1=Ev+Es+Ek+Dk+DR+Dc+Ds (12) E2=Ev+Es+Ek+Dk+De+DR+DRe (13) 式中:Ev為結構自身阻尼耗能;Es為結構勢能;Ek為結構動能;Dk為顆粒群動能;De為顆粒群與結構垂直的碰撞耗能;DRe為因顆粒群轉動引起的碰撞耗能;DR為顆粒群慣容對應的轉動動能;Dc為顆粒群與結構之間碰撞阻尼耗能;Ds為顆粒群與結構之間的碰撞彈性勢能。以上變量計算公式如下所示。 (14) (15) (16) (17) (18) (19) (20) (21) (22) 式中:vη為第η次碰撞時刻兩個碰撞質量的相對速度;n為碰撞次數。 自由振動過程中系統能量累加曲線如圖12所示。圖12中:Em為EISM對應的累加系統機械能,為結構勢能Es、結構動能Ek、顆粒群動能Dk、顆粒群慣容對應轉動動能DR之和;En為EISM-CE對應的累加系統機械能,為結構勢能Es、結構動能Ek、顆粒群動能Dk、顆粒群慣容對應轉動動能DR、顆粒群與結構之間的碰撞彈性勢能Ds之和。 圖12 結構體系能量變化規律Fig.12 Energy change rule of controlled system 由圖12可知,前期顆粒運動較為劇烈,顆粒群與碰撞板的碰撞次數較多,因此前期顆粒群碰撞耗能較為充分,對應結構自身的總能量(Ev+Es+Ek)衰減較快。系統穩定后,EISM-CE對應的能量比Ev∶Dc=1∶1.85,EISM對應的能量比Ev∶De∶DRe= 1∶0.59∶0.5。總體來看,自由振動的能量耗散主要是以顆粒與結構的相互作用的方式進行耗散。另外需要注意的是,由于EISM-CE考慮了碰撞過程中的時間效應,碰撞初期EISM-CE耗能能力更加充分,因此能量趨于穩定的時間更短。 在共振激勵下,進行NPPD減振性能分析,激勵幅值取0.03g,基于數值仿真可得結構位移時程曲線如圖13所示。由圖13可知,簡諧激勵下NPPD具有較好的減振效果。系統穩定后EISM對應減振性能略優于EISM-CE對應減振性能,這一定程度上說明碰撞恢復系數相比較于接觸單元耗能更加高效。時程曲線詳細分析表明,由于EISM-CE對應碰撞間距較小,且采用接觸單元法模擬碰撞過程中顆粒群與結構之間的相互作用,系統非線性相對較小,因此對應等效集中質量能夠更快速地趨于穩定。相比之下,EISM對應等效集中質量趨于穩定較慢,且存在一定的分叉現象。 圖13 簡諧激勵下位移時程曲線(ω=ωn)Fig.13 Displacement time history curve under harmonic excitation (ω=ωn) 簡諧激勵下系統能量累加曲線如圖14所示。由圖14可知,系統穩定后EISM-CE對應Ev∶Dc=1∶2.79,EISM對應的Ev∶De∶DRe=1∶1.64∶1.39。對于EISM-CE而言,系統能量主要通過c1耗散,而EISM主要是通過顆粒群與結構之間的垂直碰撞耗能和顆粒群轉動引起的耗能所耗散。 圖14 簡諧激勵下能量變化規律Fig.14 Energy change law under harmonic excitation 選取El-Centro地震動記錄、Kobe地震動記錄及Taft地震動記錄作為振動臺輸入,并調整地震動記錄峰值為0.20g,進行減震效果分析。El-Centro及Taft地震動記錄作用下受控結構及原結構的位移時程曲線,如圖15所示。不同力學模型減震效果特征值統計如表3所示。分析可知,NPPD對最大位移響應及均方根位移響應均具有一定的減震作用,其中RMS對應的減震效果優于最大位移對應的減震效果。這是在瞬態響應下,阻尼器無法充分發揮減振性能導致。其中,需要注意的是,由于Kobe地震動記錄的頻譜范圍較寬,對其減震效果并不理想。不同模型對應減震效果分析結果表明,考慮碰撞時間效應后,EISM-CE對應減震效果略優于EISM模擬結果。 表3 地震作用下受控結構減振效果分析 圖15 多顆粒阻尼器減震效果分析Fig.15 Damping effect analyses of M-PD El-Centro及Kobe地震動下系統能量累加曲線如圖16和圖17所示。由圖16和圖17可知:在振動初期,結構運動幅值較小,顆粒群運動并不充分,阻尼器的動能及勢能較小,對應NPPD并未充分發揮其減震性能;隨著結構響應的增加,顆粒運動劇烈程度逐漸增加,NPPD減震性能逐漸增加。與Kobe地震動記錄相比,El-Centro及Taft地震動記錄下結構的動能、勢能穩定發展,顆粒與結構之間的阻尼耗能更加充分,對應減震效果更加明顯。 圖16 El-Centro地震動下系統能量累加曲線Fig.16 Energy accumulation curve of system under El-Centro input 圖17 Kobe地震動下系統能量累加曲線Fig.17 Energy accumulation curve of system under Kobe input 地震作用下不同力學模型結構的自身耗能與對應阻尼器耗能占比如表4所示。表4中,Ein為外部輸入能量。EISM-CE與EISM對應的Ein分別為E1和E2。分析結果表明,不同地震動記錄下,EISM-CE模型對應系統能量主要通過顆粒群碰撞阻尼進行耗散。受地震動差異性影響,不同地震動記錄下能量耗散占比有所區別,其中Kobe地震動記錄下阻尼器耗能占比最大,Dc/Ev=2.42。不同力學模型對應耗能占比分析結果表明,與EISM-CE相比,EISM對應結構自身耗能占比總體高于阻尼器自身耗能占比。EISM對應減震機理與EISM-CE對應減震機理存在一定的差異性。在EISM作用下,顆粒碰撞一定程度上激起了結構響應,使得結構自身耗能占比提升。相比之下,EISM-CE主要通過顆粒群自身進行耗散。 表4 耗能成分對比Tab.4 Comparison of energy consumption 單位:% 在現有考慮慣容的等效單顆粒模型(EISM)研究基礎上,本文提出了基于接觸單元法的等效慣性單顆粒力學模型(EISM-CE)。試驗及數值仿真分析結果表明,本文提出的EISM-CE同樣能夠較好地模擬NPPD減振性能,模型等效原則及物理參數取值原則是合理有效的。具體結論如下: (1) 簡諧激勵作用下,不同填充率對減振效果影響分析表明,當γ=30%時,顆粒與結構未發生充分碰撞,此時減振效果較弱;隨著填充率的逐漸增加,減振效果呈現先增加后減小的趨勢,當γ=90%時,減振效果最優;隨著γ的進一步增加,雖然顆粒與容器壁的碰撞次數逐漸增加,但沖擊力逐漸減小,顆粒群無法充分發揮耗能能力,致使NPPD減振效果降低。 (2) 與EISM相比,EISM-CE考慮了碰撞過程中的時間效應,位移放大系數頻響曲線擬合更加光滑。簡諧激勵及地震作用下等效模型試驗驗證綜合表明EISM-CE能夠更加合理地反映NPPD的減振效果及機理。 (3) 減振性能數值分析結果表明,NPPD具有良好的減震效果。不同力學模型對比分析結果表明,由于力學模型的差異性,不同力學模型展示的NPPD的減振性能及機理存在一定的差異。在簡諧激勵下,系統穩定后EISM對應阻尼器耗能占比高于EISM-CE對應阻尼器耗能占比。相比之下,在自由振動及地震動作用下,EISM-CE對應阻尼器耗能占比高于EISM對應阻尼器耗能占比。需要注意的是,在地震動作用下,EISM-CE對應阻尼器耗能占比高于結構自身耗能占比,這與EISM存在一定差異。地震動作用下,碰撞時間效應的引入所展現的NPPD減震機理差異性更加明顯。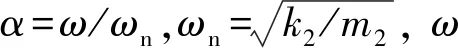
1.3 碰撞階段體系的運動方程
2 等效力學模型的試驗驗證
2.1 試驗設計

2.2 模型參數等效原則
2.3 簡諧激勵下等效模型試驗驗證
2.4 地震動作用下力學模型試驗驗證
3 基于等效模型的NPPD減振性能分析
3.1 自由振動
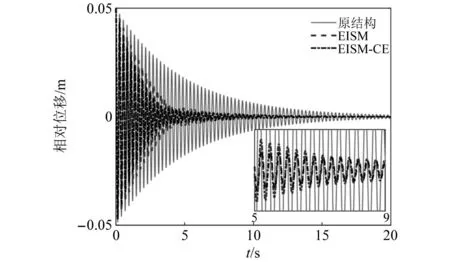
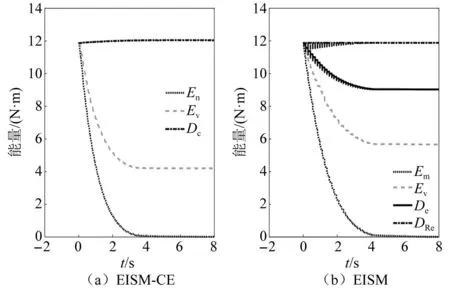
3.2 簡諧激勵
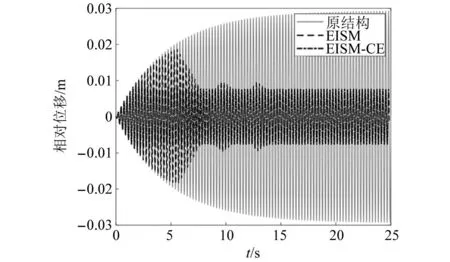
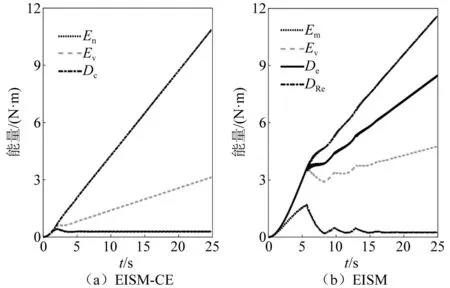
3.3 地震動作用

4 結 論

